基于改进在线极限学习机的短时交通流预测模型研究*

周伯荣，程伟国，许镇义，温秀兰

(1.南京工程学院自动化学院,江苏 南京 211100；2 南京交通职业技术学院汽车工程学院,江苏 南京 211100；3.合肥综合性国家科学中心人工智能研究院,安徽 合肥 230088；4.中国科学技术大学信息科学技术学院,安徽 合肥 230026)

1 引言

随着智能传感技术、大数据、云计算和人工智能技术的快速发展，智能交通系统ITS(Intelligent Transport System)在我国城市道路交通管理中得到广泛应用。2019年印发的《交通强国建设纲要》明确提出要大力发展智慧交通，推动大数据、互联网、人工智能、区块链和超级计算等新技术与交通行业深度融合[1]。交通流信息预测作为ITS进行交通疏导管理的重要基础，通过对获取的实时、完整、全路况道路交通信息进行分析和预测，可以有效反映城市路网的运行状态，为城市交通管理规划提供可靠的数据支持和科学的决策依据[2]。因此，针对短时交通流预测是智能交通领域的重要研究方向。

目前，国内外相关学者针对短时交通流预测问题提出了各种预测模型和方法，按方法类型特点主要分为基于数理统计理论模型的预测方法、基于数据驱动的学习模型预测方法和基于微观交通仿真的预测方法。基于数理统计理论模型的预测方法是一种参数化方法，主要利用历史交通流统计数据拟合出含参数的数理统计模型，此类方法主要有时间序列模型[3,4]、灰色理论预测模型[5]和卡尔曼滤波预测模型[6,7]等。该类方法依赖于模型参数的假设检验，难以刻画交通流非线性动态演变过程。基于数据驱动的学习模型预测方法是一种非参数化方法，无需进行模型假设检验，利用历史交通观测数据构建相应的机器学习预测模型来拟合交通流的动态演变过程。此类方法主要有支持向量回归预测模型[8,9]、神经网络预测模型[10,11]和深度学习预测模型[12 -14]等。支持向量回归模型依赖于参数选择和核函数选取，限制了其对复杂交通流的模型表示能力;神经网络和深度学习预测模型存在模型过拟合问题，并依赖于大量交通数据样本，网络训练时间长、计算资源消耗量大，无法实现交通流预测模型的在线动态更新。基于微观交通仿真的方法采用计算机搭建微观交通仿真环境模拟实际道路的交通状况，进而实现交通流预测[15]，但其计算复杂度高，难以模拟大规模路网交通系统，预测实时性差。

现有的研究大都集中在不改变历史观测数据集的情况下构建交通流预测模型，由于交通流量数据是实时更新的增量流数据，每次更新历史数据集时都需要重新构建预测模型，需要消耗大量计算资源和运行时间。本文旨在构建一种简单快速的交通流预测模型，在有效缩短模型构建时间、满足预测实时性的基础上，利用实时交通流数据动态更新交通流预测模型。极限学习机ELM(Extreme Learning Machine)因其具有简单的平层网络结构、可以快速增量建模的特点，成功应用于各种分类和回归任务中[16,17]。因此，本文提出一种基于改进在线顺序极限学习机的交通流预测模型IOS-ELM(Improved Online Sequential ELM)，通过构建新增数据的增强特征映射关系，生成交通流动态更新特征表示空间，实现短时交通流预测模型的动态更新。

2 相关基础知识

2.1 极限学习机模型

ELM是一种单隐藏层前馈网络SLFN(Single-hidden Layer Feed-forward Network)学习算法[18]，包括输入层、单隐藏层和输出层。图1给出了一个包含k个隐藏层节点的ELM模型实例，其中，W=[w1,w2,…,wk]和B=[b1,b2,…,bk]分别是输入层到隐藏层的权重矩阵和偏置向量，β是隐藏层到输出层的权重,X和Y为输入和输出矩阵。

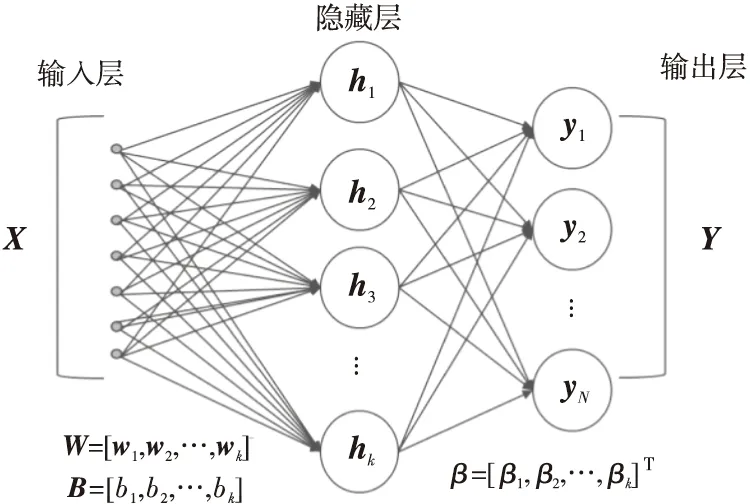
Figure 1 Structure of extreme learning machine图1 极限学习机结构

ELM的学习过程描述为在大小为N的训练数据集上通过最小化经验误差来训练一个具有随机隐藏层节点的单隐藏层前馈神经网络。给定的任意一条训练样本(xi,yi)，其中xi∈Rn，yi∈Rm,则对于一个具有k个隐藏层节点的ELM模型的输入和输出之间的映射关系可由式(1)表示:

i=1,2,…,N

(1)

其中，βj∈Rm是隐藏层到输出层权重，gj(·)和g(;)是隐藏层的非线性激活函数。

进一步地，式(1)可以写成矩阵形式，如式(2)所示：

Hβ=Y

(2)

其中，

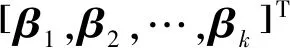
其中，g(·)是非线性激活函数。

ELM的学习算法是基于最小化经验误差进行训练，往往存在过拟合问题，导致泛化能力不强。通常在优化问题中额外增加结构化风险，该目标优化问题可表示为式(3)所示：

(3)

由于是随机化输入层到隐藏层权重和偏置(wi,bi)，并在整个学习过程中保持不变，ELM的训练过程实质上是结合广义逆矩阵直接求解隐藏层到输出层的权重β，其求解如式(4)所示：

β=H+Y=(HTH+I/C)-1HT

(4)

其中，H+是隐藏层矩阵H的伪逆矩阵;I是单位矩阵;C是正则化常数,用于避免HTH出现奇异矩阵，提高ELM稳定性。由于ELM是一种结构相对简单的模型，在实际任务场景中需要针对应用问题特点，对模型进行优化和改进。

2.2 基于增量学习的极限学习机

有关增量学习ELM的研究主要包括基于模型结构增量的ELM[19]和基于数据增量的ELM,即OS-ELM(Online Sequential Extreme Learning Machine)[20]。基于模型结构增量的ELM通过在SLFN中新增隐藏节点对网络进行更新，以克服ELM初始设置隐藏层节点数不足导致模型数据表示能力不足的问题。每次更新前后的网络变化可表示为式(5)所示：

fn(x)=fn-1(x)+βngn(x)

(5)

其中，fn是更新后网络模型，fn-1是更新前网络模型，gn(·)是新增隐藏层节点的非线性激活函数。为了提高更新后的网络性能，需要在原有网络模型基础上进一步减小网络误差，则新增隐藏层节点权重可表示为式(6)所示：

(6)

其中，en-1表示新增节点前的模型误差。

基于模型结构增量的ELM通过新增隐藏层节点修改网络结构来实现ELM模型的自动构建,其需要固定的数据集，适用于离线学习的有监督学习任务。

基于数据增量的OS-ELM通过数据变化来递推顺序更新隐藏层权重，以适应训练数据不断更新的场景。与经典ELM一样，OS-ELM在初始化时设置隐藏层节点数，并利用递归最小二乘顺序更新隐藏层权重，如式(7)所示:

(7)

其中，Mk用于保存中间计算结果，hk+1是新增数据在隐藏层的输出，yk+1是新增数据标签。OS-ELM可以根据新增数据逐条或逐块更新模型，以适应不同应用场景中数据的变化。

3 基于改进在线顺序极限学习机的交通流预测模型IOS-ELM

为了提高OS-ELM对短时交通流的预测性能，本文在基础ELM网络中引入自编码器AE(Auto-Encoder)和循环递归神经网络结构RNN(Recurrent Neural Network)，提出了一种基于改进在线顺序极限学习机交通流预测模型(IOS-ELM)，如图2所示，将整体数据进行分块后送入在线顺序极限学习机，Xi是第i块数据,Yi是数据块Xi的预测输出。该模型结构主要包括以下3个部分：

(1)递归极限学习RELM(Recurrent Extreme Learning Machine)网络结构单元用于提取短时交通流的时序变化特征；

(2)ELM用于学习RELM输入层权重RELM-IW(Recurrent Extreme Learning Machine Input Weight)和隐藏层权重RELM-HW(Recurrent Extreme Learning Machine Hidden Weight)；

(3)同时在ELM中附加自编码器单元ELM-AE(Extreme Learning Machine AutoEncoder),用于学习ELM的输入层到隐藏层权重和偏置参数,以替代随机初始化操作。

Figure 2 Structure of IOS-ELM 图2 IOS-ELM结构

IOS-ELM学习过程包含初始化阶段和在线顺序学习阶段。在初始化阶段，常规的ELM模型使用部分训练集N0离线训练ELM，其输出权重计算如式(8)所示:

(8)

为使得ELM完全利用增量数据在线学习，本文在其初始化阶段不使用任何训练数据，则式(8)改写为式(9)所示:

β0=0，P0=(I/C)-1

(9)

对于RELM单元，其初始隐藏层到输出层权重β0和P0按式(9)进行初始化，隐藏层权重H0根据随机高斯分布初始化。对于输入层和隐藏层权重也采取同样的操作。

(10)

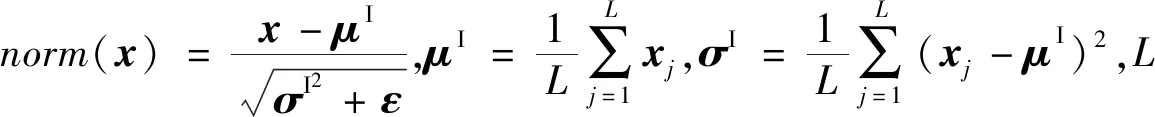
(11)

(12)

(13)

对权重Hk+1的更新计算方式如式(14)所示：

(14)

最后，对IOS-ELM的输出层权重βk+1的更新计算方式如式(15)所示：

βk+1=βk+Pk+1(Hk+1)T(Yk+1-Hk+1βk),

Pk+1=

Pk-Pk(Hk+1)T(I+Hk+1Pk(Hk+1)T)-1Hk+1Pk

(15)

对于ELM-AE单元，通过将目标预测输出设置为与输入相同，即令Y=X，则输入层到隐藏层的权重矩阵W′=[w1,w2,…,wk]和偏置向量B′=[b1,b2,…,bk]随机初始化满足式(16)：

W′TW′=I,

B′TB′=1

(16)

隐藏层到输出层的权重β的计算方式与ELM相同，如式(17)所示：

β′=H+Y=H+X=(HTH+I/C)-1HT

(17)

并将β′作为ELM-AE单元输入权重向量,以替代随机初始化操作,如式(18)所示：

W=β′，

B=0

(18)

4 实验与结果分析

4.1 长沙市交通流数据集

本文选取长沙市芙蓉区远大一路局部路段车流量作为IOS-ELM的评估数据集，研究路段如图3所示。路段车流量由车道环行线圈检测器实时采集，采样时间间隔为5 min，并将采集的数据存入历史数据集中。收集的历史数据为2013年9月17日～2013年10月6日共20天的交通流数据。图4展示了工作日和周末的日车流量变化，可以看出每日车流量基本呈现双峰分布(早高峰和晚高峰)，日车流具有相似的变化模式。

在实验中，本文设置IOS-ELM的输入向量维度为100时间步长(500 min)，输出向量维度为1个时间步长，即给定历史500 min交通流观测数据预测未来5 min的交通流变化。采用零均值标准化方法对原始数据进行预处理，模型的预测性能评价指标采用标准均方根误差NRMSE(Normalized Root Mean Square Error)和平均绝对百分比误差MAPE(Mean Absolute Percentage Error)，其计算方式如式(19)和式(20)所示：

(19)

(20)

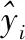
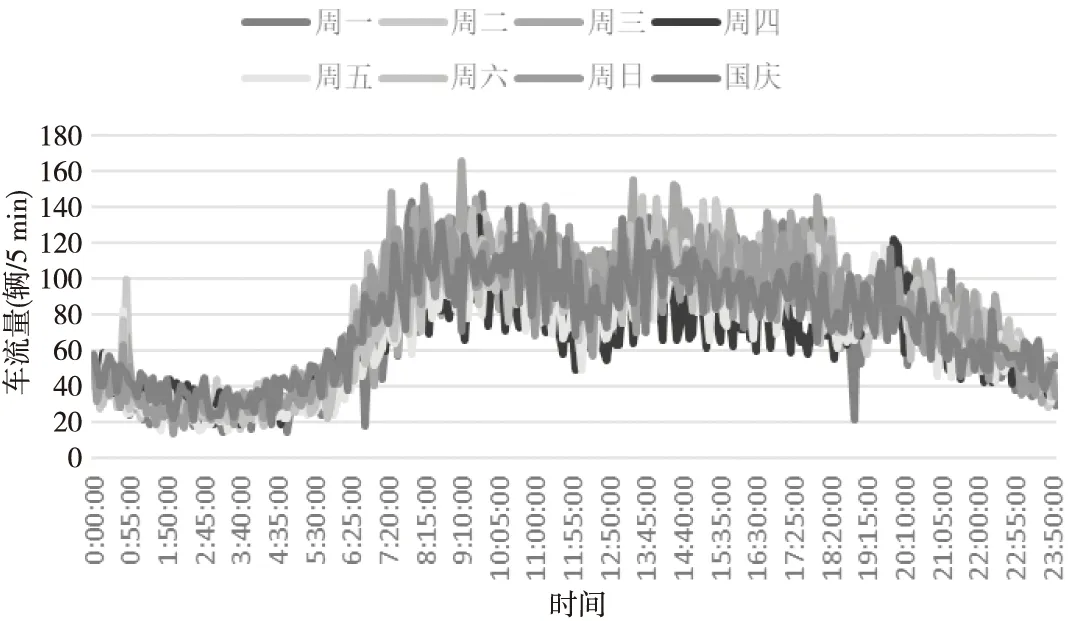
Figure 4 Daily changes of traffic flow on different working days图4 不同工作日车流量日变化

4.2 对比实验

本文实验在一台高性能服务器上进行，其具体实验环境参数配置如表1所示。

为了验证本文IOS-ELM模型的性能，与以下基准方法预测模型进行比较。

(1)SVR(Support Vector Regression)支持向量回归预测模型，适用于小样本的在线实时预测。

Table 1 Experiment environment表1 实验环境配置

(2)多层感知机MLP(Multilayer Perceptron)是一种典型的前馈神经网络模型，其能学习任意非线性函数映射。因此,本文提取时间上临近的100个时刻观测序列作为MLP模型的输入特征。

(3)ELM是一种单隐藏层前馈网络学习模型，具有可以快速增量建模的特点，已成功应用于各种分类和回归任务中[22]。

(4)OS-ELM是一种基于ELM的在线学习模型，适用于时间序列预测任务。

图5给出了SVR、MLP、ELM、OS-ELM和IOS-ELM在远大一路路段交通流预测结果与实际交通流量对比；图6给出了不同模型在2013年10月4日～10月6日国庆期间的预测结果与实际交通流量的对比。从图5和图6中可以看出,IOS-ELM可以较好地跟踪目标路段短时交通流量的变化。

Figure 5 Comparison of daily traffic flow prediction图5 日车流量预测对比

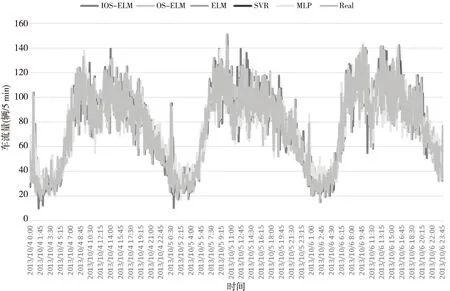
Figure 6 Traffic flow prediction on 2013/10/4～2013/10/6图6 2013年10月4日～10月6日交通流预测结果

表2给出了不同模型的具体预测性能指标对比，从对比结果可以看出，本文设计的IOS-ELM模型在NRMSE和MAPE性能指标上均超过了其他基准预测模型(SVR、MLP、ELM和OS-ELM)的。虽然IOS-ELM在预测耗时上劣于OS-ELM和SVR，但是其在NRMSE和MAPE性能指标上均有明显提升，同时确保了一定的实时性。同时,MLP模型需要大量训练耗时，在小样本上也无法取得较好的预测精度，其预测性能在所有模型中表现最差。

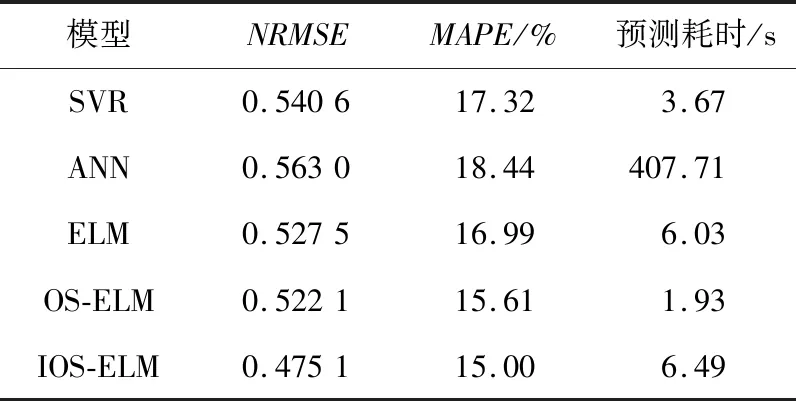
Table 2 Comparison of prediction performance of different models表2 不同模型预测性能对比

5 结束语

为了实现城市短时交通流的实时准确预测，本文基于极限学习机相关理论提出了一种基于改进在线极限学习机的城市路段短时交通流预测模型，通过引入自编码器权重学习机制来取代输入层和隐藏层的随机初始化权重，并利用循环递归神经网络单元学习隐藏节点特征的时序依赖性。最后在长沙的实际道路交通数据集上评估本文所设计的IOS-ELM模型，与SVR、ANN、ELM和OS-ELM等模型相比，IOS-ELM模型的NRMSE和MAPE最小，同时预测耗时也较小，可以保证一定的实时性，满足城市道路交通流的实时准确预测需求。