改进灰狼算法优化支持向量机的入侵检测研究

欧元芳 缪祥华，b

（昆明理工大学a.信息工程与自动化学院；b.云南省计算机技术应用重点实验室）

入侵检测系统是计算机网络信息的安全卫士，能够检测出网络入侵行为，及时发出警告并做出响应， 可以有效避免网络安全事故的发生。目前，常用的入侵检测方法是利用收集到的入侵检测数据进行建模，有效地对各种网络攻击行为进行分类，以便及时采取安全防范措施［1］。

目前，研究人员将基于深度学习和基于机器学习的算法（如K近邻［2］、决策树［3］、极限学习机［4］及支持向量机 （Support Vector Machine，SVM）［5］等）应用于入侵检测。

Vapnik V N提出SVM后， 就有许多研究者将其用于入侵检测领域，并且取得了较好的成效［6］。徐雪丽等将CNN-SVM模型应用于入侵检测，首先将预处理好的二维数据输入到CNN中学习有效特征，后面通过SVM将低维特征进行分类，准确率和训练速度都优于GRU-Softmax模型［7］。 虽然SVM具有强大的分类能力，但在面对高维、非线性特征时无法展现其良好的性能。 因此，要解决SVM进行入侵检测分类面临的“维数灾害”［8］，就必须对高维数据进行降维，获得有表征性的低维特征，再输入到SVM中充分发挥其强大的分类性能。

在网络流量大、复杂的网络环境下，入侵检测识别率、稳定性都得不到保证［9］。 近些年，越来越多的研究人员采用深度学习算法进行特征提取，效果较好。Javaid A等使用SAE进行特征提取，采用Softmax分类器进行分类识别［10］。 郭旭东等将改进的稀疏去噪自编码器（ISSDA）应用于入侵检测，在ISSDA中加入了新的约束，提高了其解码能力，得到了有效的特征抽象表达［11］。

面对高维、海量数据，为提高入侵检测的分类性能， 笔者提出首先使用降噪自编码器（Denoising Autoencoder，DAE）进行特征提取；然后使用随机动态调整收敛因子的灰狼算法（IGWO）去寻找SVM的最优参数，用获得的最优参数建立性能较优的分类模型——IGWO-SVM， 以期提高入侵检测分类精度。

1 相关理论

1.1 DAE

DAE通过对输入数据加入噪声， 经过编码、解码得到无噪声原始数据。 这样的过程能够提高模型的抗干扰能力，具有较高的鲁棒性，提取到的特征更本质、更具代表性。 相比于传统自编码器 （AE），DAE能够重构含有噪声的输入数据，这一过程使提取的低维特征更具代表性、更本质和更具鲁棒性。

其中，w和b′分别为编码器的权重和偏置。

对式（1）中特征提取结果h进行解码，可得：

其中，w*和b*分别为解码器的权重和偏置，w*=wT。

1.2 SVM

SVM的实现就是一个分类过程，是寻找出一个超平面，将不同类别的样本分开。

对于线性可分数据集（xi，yi），i=1，2，…，n，xi∈Rn，yi∈{-1，1}，它分类的超平面是：

其中，ω为分类超平面的系数向量，b为偏移量。

求最优超平面可转化为一个凸二次规划问题：

其中，εi是松弛向量，C是惩罚系数。

引入拉格朗日乘子ai，将式（4）转化为对偶形式：

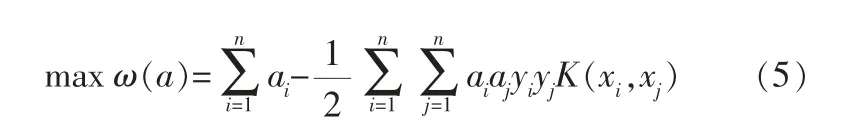
且满足约束条件：

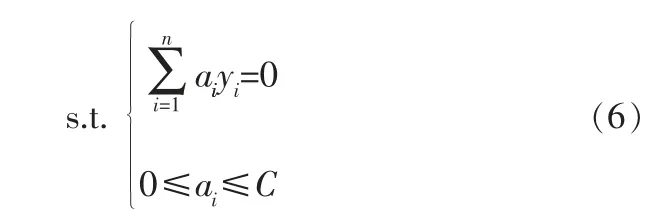
其中，K（xi，xj）为核函数。

相应的决策函数为：

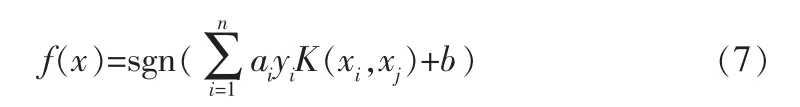
本研究采用RBF高斯核函数，其公式如下：

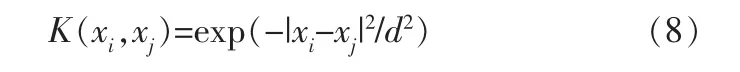
其中，d为核参数。

1.3 灰狼算法

灰狼优化 （Grey Wolf Optimization，GWO）算法是依据灰狼捕食猎物而开发的一种智能优化算法［12］。 灰狼优化算法中的狼群被分为α′、β′、δ′和ω′4类。 其中α′狼是头狼，是最高领导者；β′是α′的下属狼， 服从并辅助α′做决策；δ′听从α′和β′的决策命令；最底层是ω′，服从α′、β′、δ′狼，并通过α′、β′、δ′狼的位置寻找猎物。

灰狼捕食猎物的行为定义为：

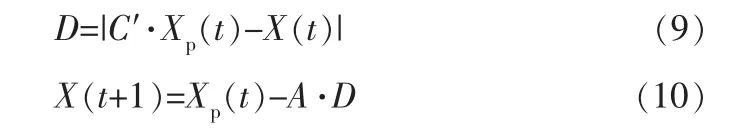
其中，D为狼群个体与猎物之间的相对距离，t为当前迭代次数，X（t）为狼的当前位置，Xp（t）为猎物的当前位置。

系数向量A和C′可表示为：

其中，r1，r2分别为［0，1］之间的随机数，收敛因子a是从2线性递减至0，即：

其中，tmax为最大迭代次数。

群体中其他灰狼个体根据α′、β′、δ′的位置分别更新各自的位置，即有：

其中，X1、X2、X3表示ω′分别向α′、β′、δ′方向的位移量，X（t+1）是灰狼个体ω′的位置，X′是灰狼当前的位置，Xα′、Xβ′、Xδ′分别为灰狼α′、β′、δ′的位置。

1.4 随机动态调整收敛因子的灰狼算法（IGWO）

在基本GWO算法中，当|A|＞1时灰狼分散在各区域，希望寻找更好的猎物，即全局勘探；当|A|＜1时灰狼集中在某个区域对猎物进行最后攻击，即局部搜索［13］。

由式（11） 可知，A的取值受收敛因子a的影响。 收敛因子a采用线性递减策略，如果在迭代前期找不到合适的a，算法容易陷入局部最优，达不到收敛精度。 因此，笔者提出随机动态调整收敛因子的灰狼算法。 采用随机选取收敛因子a的方式，可得相对较大的a值，避免在迭代过程中群体只集中在某个区域寻找猎物， 陷入局部最优；迭代后期，随机选取方式可以得到相对较小的a值，有利于加快寻优速度，提高收敛精度［14］。 笔者设计的随机调整收敛因子策略为：

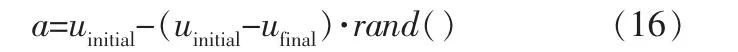
其中，uinitial和ufinal分别为收敛因子a的初始值和终止值，uinitial=2，ufinal=0；rand（）为0～1之间的随机数。

2 入侵检测模型的整体流程

如图1所示，入侵检测模型的整体流程包括3部分： 数据预处理、DAE进行特征提取和IGWOSVM分类模型构建。

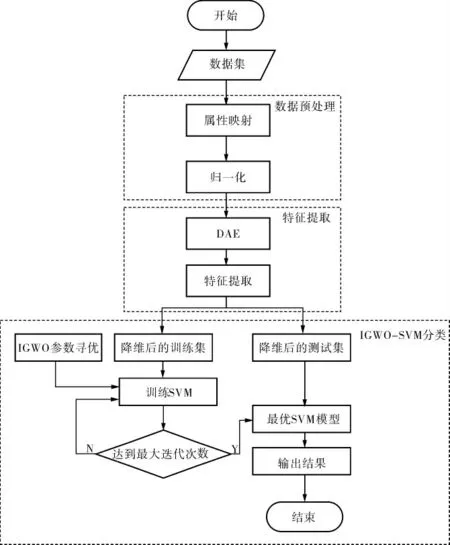
图1 入侵检测模型的整体流程

2.1 数据预处理

首先采用独热编码（one-hot code）的方法将原数据集中的字符特征数值化，然后对特征进行归一化处理。

2.2 特征提取

使用DAE对预处理好的数据进行特征提取。笔者设计的DAE主要由编码结构和解码结构组成。 输入部分是随机抽取KDD CUP99数据集的2%， 经过独热编码等预处理后得到的109维数据。 首先，在编码阶段，对含噪声的数据进行编码，得到低维特征；然后在解码阶段对低维特征解码重构，通过最小化重构误差对DAE的参数进行调整， 使用梯度下降法对权重参数进行更新，逐层训练，反复迭代［15］。 训练结束后，保存低维特征，达到数据降维的目的。

2.3 利用IGWO优化SVM的分类模型构建

当SVM的参数C和g取值不同时，SVM的分类性能区别很大。 要得到高维空间的最优分类模型，需要选择合适的SVM参数［16］。 因灰狼算法实现简单、参数少，且在收敛性、寻优性等方面优于PSO、DE等算法［17］。 故选择灰狼算法寻找SVM的最优参数。 IGWO-SVM分类模型流程如图2所示。

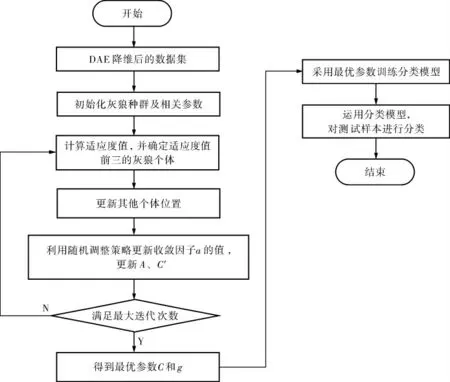
图2 IGWO-SVM分类模型流程

IGWO-SVM分类模型的具体步骤如下：

a. 将预处理好的数据集送入DAE进行降维，得到降维后的训练集和测试集。

b. 初始化IGWO的种群规模、最大迭代次数、uinitial和ufinal的值，同时对SVM中的参数C和g进行编码，成为狼群中位置的两个维度。

c. 计算适应度值，确定适应度值排名前三的个体，即α′狼、β′狼和δ′狼。 将错误率fitness作为适应度值，fitness=2-ACCtest-ACCtrain，其中，ACCtest表示测试集的准确率，ACCtrain表示训练集的准确率。

d. 更新灰狼个体位置。

e. 根据式（16）更新a，根据式（11）、（12）更新A和C′。

f. 验证是否满足最大迭代次数，若满足则转到步骤g；否则，返回步骤c。

g. 输出SVM的最优参数（C，g）。

h. 采用最优参数训练分类模型。

i. 运用IGWO-SVM模型对测试集数据进行分类。

3 实验与分析

3.1 实验数据与数据预处理

本次实验采用的是KDD CUP99数据集，每条数据由41个特征和1个标签构成［18］。 标签属性可分为5类：Normal、U2R、DOS、R2L和Probe， 其中，Normal是正常类，其余4类是异常类。

考虑到SVM在处理小样本方面性能较优，由于KDD CUP99数据集样本相对较大，故从10%的KDD CUP99数据集中抽取2%得到训练集，从Corrected数据集抽取2%得到测试集。 由此可以得到9 880条训练集，6 221条测试集。对随机抽取的数据集进行预处理的过程如下：

a. 字符特征的数值化。采用独热编码的方式对字符型数据进行特征映射。 例如，其中protocoltype的3种协议类型可表示为TCP=［1，0，0］，UDP=［0，1，0］，ICMP=［0，0，1］。 类似地，将service字符特征和flag字符特征进行独热编码。

3.2 实验评价指标

本实验采用准确率（ACC）、召回率（DR）、精确率（PR）、误报率（FPR）和F1-measure（F1）作为评价指标，其公式为：

其中，TP是将异常类预测为异常类的数据量，TN是将正常类预测为正常类的数据量，FP是将正常类预测为异常类的数据量，FN是将异常类预测为正常类的数据量。

3.3 实验过程及结果分析

3.3.1 压缩维度对模型的影响

进行实验1的目的是， 在保证较高的准确率时，使用DAE选择相对较小的特征向量维数。 含噪声的输入特征向量经过DAE隐含层的重构，得到隐含层的向量可以看作是输入数据的压缩。 其中，选择压缩维度从5变化到9，即特征个数从5到9进行实验对比，压缩维度对模型的影响见表1。

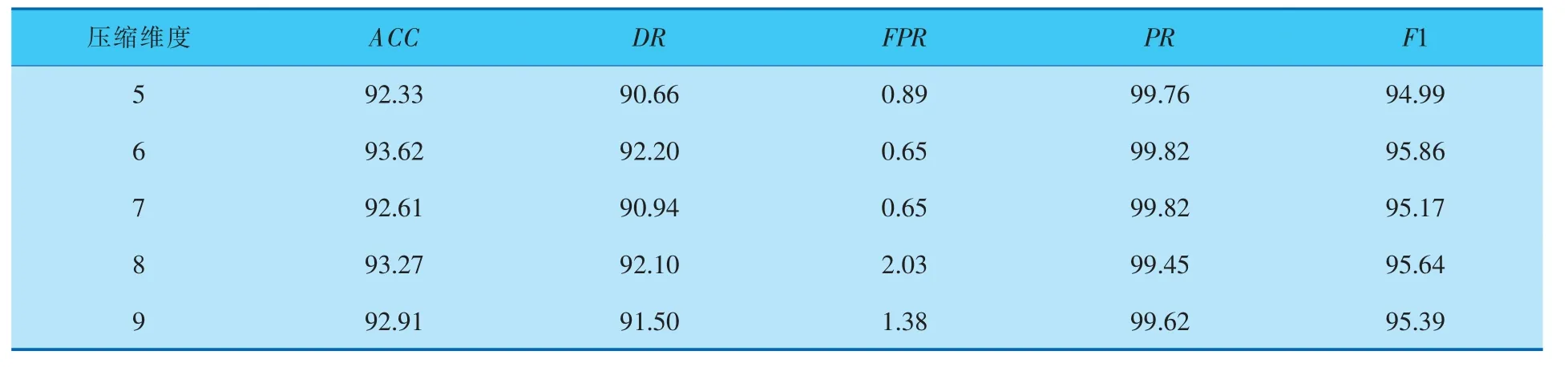
表1 压缩维度对模型的影响 %

由表1可知，DAE-SVM模型将数据降维为6个特征时，准确率（ACC）和召回率（DR）是最高的，其中误报率（FPR）也是最低的。该实验表明，使用DAE特征提取后得到相对较少的维度数就具有很强的表征性，可获得较优的分类性能。

3.3.2 不同特征提取方法的对比

为验证DAE特征提取的可取性，在确保使用SVM作分类器的同等情况下， 使用主成分分析（PCA）、独立成分分析（ICA）和奇异值分解（SVD）3种特征提取方法进行实验对比，结果见表2。

表2 不同特征提取方法实验对比 %

从表2可以看出，DAE在准确率（ACC）、召回率（DR）及误报率（FPR）等指标上都优于其他特征提取方法。 该实验说明，与PCA-SVM、ICA-SVM等常用降维算法相比，DAE能够有效利用次要特征中的重要信息，而不是一味舍弃次要特征。 因此， 采用DAE进行特征提取得到的低维抽象特征，更有利于分类［19］。

3.3.3 IGWO的SVM参数优化

入侵检测数据集使用DAE降维后， 在GWOSVM和IGWO-SVM上寻找SVM的最优参数C和g时的适应度值的变化情况如图3所示。其中，GWO和IGWO算法的种群规模为20，最大迭代次数为25，以错误率fitness作为适应度值， 错误率越小则结果越优。

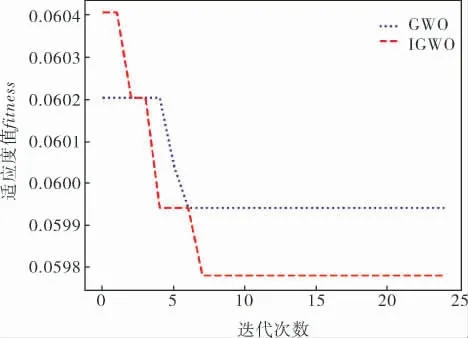
图3 两种模型的最佳适应度曲线

由图3可知，IGWO-SVM模型在迭代前、中、后期适应度值都有波动，说明在寻优过程中避免了陷入局部最优解的情况。 GWO-SVM模型虽然收敛较快，但在寻优过程中波动较少，未找到最优适应度值，精度较低，且较快收敛的原因可能是陷入局部最优解。

DAE-SVM、DAE-GWO-SVM 和 DAE-IGWOSVM模型的性能比较见表3， 可以看出， 当利用IGWO来寻找SVM的最优参数C和g后，能够提高SVM的分类性能，与DAE-SVM模型相比，提高了0.978 9%的准确率（ACC），提高了1.324%的召回率（DR）。

该实验说明， 使用改进后的灰狼算法优化SVM进行分类，既能避免灰狼算法陷入局部最优解的问题，也能提高入侵检测分类的准确率和召回率，是可行有效的改进方法。

3.3.4 与不同分类算法的对比

为验证IGWO-SVM分类模型的性能， 选择极限学习机（ELM）、随机森林（RF）和AdaBoost算法作为入侵检测的分类器进行二分类的实验对比，结果见表4。

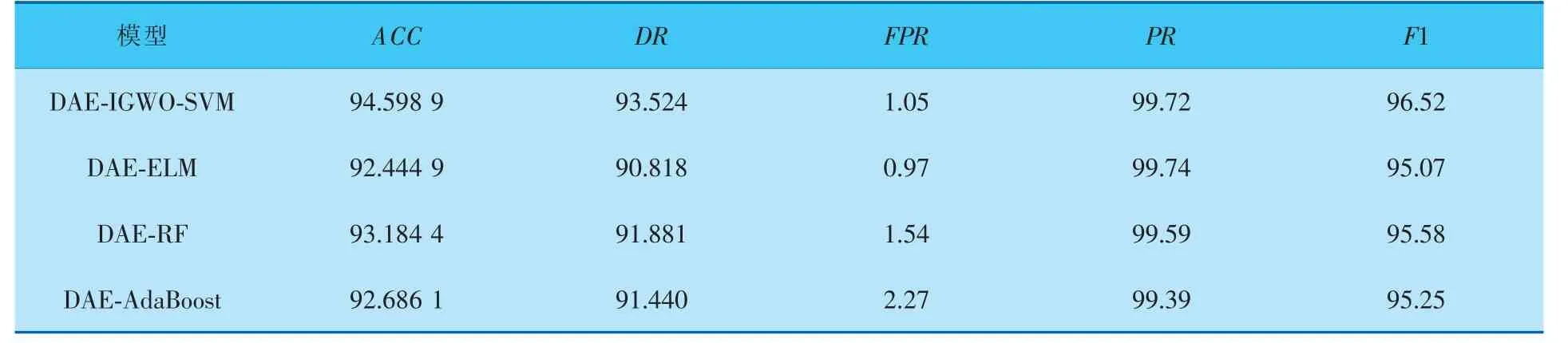
表4 不同分类算法的实验对比 %

由表4可以看出，DAE-IGWO-SVM模型的误报率（FPR）虽然略逊于DAE-ELM模型，但其准确率（ACC）、召回率（DR）和F1-measure（F1）均优于其他模型。综合来看，IGWO-SVM分类模型总体性能优于其他分类模型。

4 结束语

笔者针对SVM参数设置不当导致入侵检测分类性能不佳的问题，提出一种改进灰狼算法优化SVM的入侵检测模型——IGWO-SVM。 实验结果表明， 利用DAE对入侵检测高维数据降维后，能发挥SVM强大的分类性能；使用随机调整收敛因子的灰狼算法（IGWO），不仅能降低算法陷入局部最优的概率， 而且可以得到SVM的最优参数，提高入侵检测分类准确率、召回率及精确率等指标。

下一步， 笔者将把IGWO-SVM模型应用到入侵检测领域的其他数据集上， 同时优化模型，进一步提高入侵检测性能。