基于SPA理论的高中物理学科核心素养评价研究*

陈青雨 桑苏玲 石星星

(宁夏师范学院物理与电子信息工程学院 宁夏 固原 756000)

2018年1月，教育部颁布了《普通高中物理课程标准(2017年版)》(以下简称新课标)，2020年对其进行了修订.新课标中指出学科核心素养是学科育人价值的集中体现，是学生通过学科学习而逐步形成的正确价值观念、必备品格和关键能力；新课标将原先物理学科中的三维目标转变为物理学科核心素养“物理观念”“科学思维”“科学探究”及“科学态度与责任”四维目标[1].在此背景下，基于新课标的学科核心素养评价就成为现阶段的研究热点.文献[2]提出应从多角度、多方面、多阶段、结合多种形式来对学生探究、创新和实践进行评价.文献[3]基于文献研究法和内容分析法构建了物理学科能力评价指标体系.文献[4]基于布鲁姆教育目标分类学构建了高中物理核心素养评价体系.文献[5～7]提出应从研制试题入手对学生物理学科核心素养进行评价.文献[8]借助SOLO理论和试题特点对学生的学业质量展开合理评价.

本文在以上研究的基础上，基于新课标对学生物理学科核心素养的要求，以SPA理论为指导，构建了科学、定量的综合评价方法，并用案例对此评价方法的有效性做了说明.

1 集对分析理论

集对分析理论(SPA理论)是我国学者赵克勤提出的一种全新的系统分析方法，其核心思想是从同、异、反3个方面来研究集对的不确定性[9].所谓集对，就是把两个有联系的集合看成一个整体，集对分析也就是分析这两个集合的联系度[10～12].集对分析的基本思路是在一定的问题背景下对所论两个集合所具有的特性作同、异、反分析并加以度量刻画[13].

集对的联系度表达式为

式中N为集对所具有的特性总数；S，F和P分别为集对中两个集合相同、相异和对立的特性数.i，j和k分别表示同一度系数、差异度系数和对立度系数.文献[9]规定，S+F+P=N，i=1，k=-1，且有j∈(-1,1).

2 基于物理学科核心素养的集对分析理论

2.1 分维度评价方法

从集对分析法提出的核心思想来看，对于学生的物理学科核心素养评价，应遵循同、异、反的原则.当学生完全或基本掌握物理学科核心素养的某个维度时，那么学生在这个维度就达到了“同”的要求；反之，当学生对物理学科核心素养的某个维度完全没有或几乎没有掌握，那么在这个维度上就达到了“反”的要求；如果结果在上述两者之间，则说明达到了“异”的要求.我们规定学生物理学科核心素养的某一维度得分占此维度卷面总分80%及以上时，为“完全或基本掌握”；将占比40%及以下视为“完全没有或几乎没有掌握”；占比在40%～80%之间则为“部分掌握”.

2.2 综合评价理论

利用上面的方法可以简单的对学生物理学科核心素养的各个维度进行评价，但是如果想对学生物理学科核心素养整体有一个综合性的统计就需要更加科学、系统的方案了.文献[14]利用集对分析理论中同、异、反思想提出了一种基于SPA算法的物理实验成绩评价方法.对于普通测验成绩评价时，可以不考虑差异度、对立度，而只应对集对分析同一度概念来评价，对学生的成绩可根据集对分析的同、异、反理论来评定，最后对学生进行综合评价.

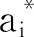
(1)

这里bmn≤1.计算物理学科核心素养的综合成绩可用平均原则确定各项指标权重W=[W1,…,Wm]，由此得到联系矩阵R=W×B，R中的元素就是i个待评R*的同一度.

得出综合成绩之后，同样将学生在物理学科核心素养得分总值占理想总值比的80%以及以上视为“完全或基本掌握”；将得分占比40%以及以下视为“完全没有或几乎没有掌握”；占比40%～80%之间视为“部分掌握”.

3 案例分析

本文选择2020年某市某中学高一年级第三次月考物理试卷作为研究案例.

3.1 物理学科核心素养情况分析

首先对试卷中的物理学科核心素养进行分析，统计物理学科核心素养各个维度及其下各个要素所涉及的题号和分值情况，为后面计算学生的物理学科核心素养得分提供依据.分析结果如表1所示.

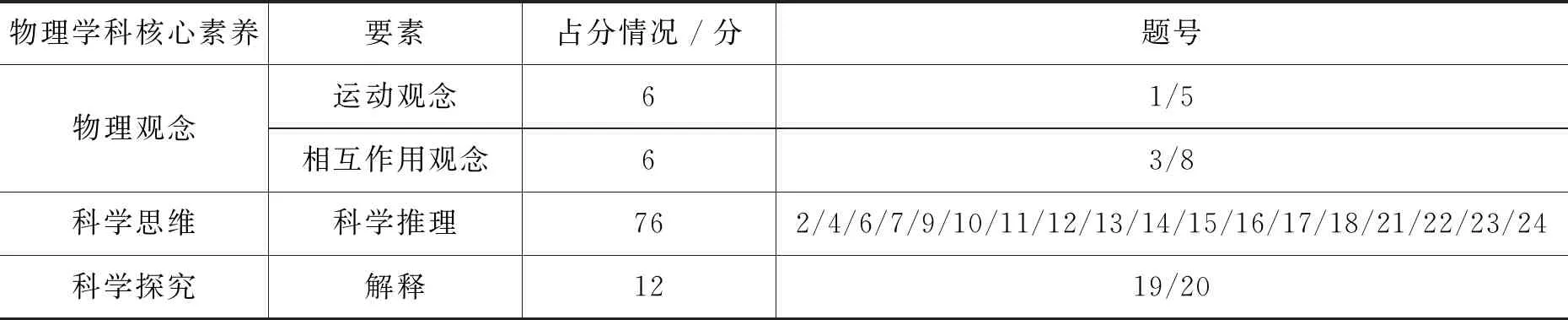
表1 试卷中物理学科核心素养各个维度细则表

我们仅举物理学科核心素养的物理观念维度做一说明.

题目1：有关牛顿第一定律说法正确的是？

该题目要求学生了解牛顿第一定律的由来，即伽利略是如何用理想实验来证明物体所受的合外力和物体运动状态之间的关系的；还要求学生对牛顿第一定律的实质及惯性有较深层次的理解.通过分析可以看出，该题考查的是物理学科核心素养物理观念维度中的运动观念.所以，该题应归为物理观念维度.

由于本次研究对象为月考试卷，所以在试卷中根据教学内容要求，重点考查了物理观念、科学思维和科学探究3个维度的情况.

3.2 全体学生各维度得分情况

下面，统计全体学生试卷中物理学科核心素养各维度总得分与试卷中物理学科核心素养该维度总分的比值.将比值满足对应条件的学生个数填入表2中对应的位置.

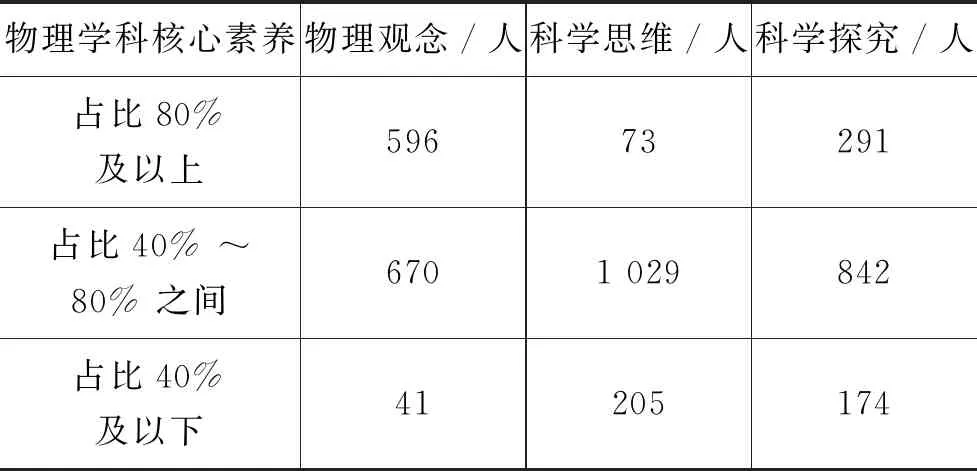
表2 试卷中学生物理学科核心素养的各个维度得分占比表

3.3 全体学生综合得分情况

统计全体学生在试卷中物理学科核心素养的综合得分情况，分析在该试卷中反映出来的学生的综合能力.

利用表1对物理学科核心素养各个维度的划分，可得出全体高一学生物理学科核心素养各个维度的得分、总得分及百分比.利用理想方案将比值满足对应占比关系的学生个数填入表3中对应位置.

表3 理想方案下全体学生试卷物理学科核心素养的得分占比表

4 分析讨论

4.1 全体学生各维度分析

物理观念

(2)

科学思维

(3)

科学探究

(4)

将式(2)～(4)中的特性数S1-P3的值分别与特性总数N进行比较，以物理观念维度为例，由于S1+F1≫P1，说明该校学生在物理学科核心素养中的物理观念维度掌握的普遍较好，中高等要求的学生(即S1+F1)数量较多；同理，对于科学思维维度和科学探究维度，处于中等要求的学生(即F2和F3)数量比较多.因此，我们可以得出结论，该校整个高一年级学生的物理学科核心素养各个维度掌握的程度都比较好.

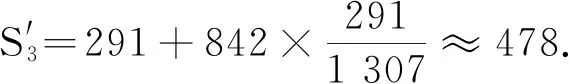
4.2 全体学生综合分析

被测1 307名学生的各项成绩构成的矩阵为A3,1 307,记为

(5)

(6)

即1 307位学生的成绩与理想方案的比值组成的矩阵.设各指标权重为

由此等式中的S4，F4，P4可知，总体上该校学生物理学科核心素养达到高等要求的学生比较少，大约占到了15.30%，中等要求的学生大约占81.48%，而低等要求的学生不到4%.

以上是学生单次月考物理学科核心素养的评价结果.如果要考查一学期甚至一学年的达成情况，可以根据学校每年月考的次数和每月对应的权重算出学生本年度月考物理学科核心素养总成绩.再者，如果将学生高一到高三每年的月考成绩都做上述的分析，再加上每年的权重，那么就可以计算出学生在高中三年的总成绩.这样不仅可以明显地看出学生在高中三年内物理学科核心素养的提高情况，也能清楚直观地看出该市该中学高中学生物理学科核心素养的达成情况.

5 结论

本文基于新课标要求，以某次月考试卷为例，对学生的物理学科核心素养达成情况进行了分析；基于SPA理论同、异、反的核心思想，评价了学生物理学科核心素养各维度和综合达成情况.通过研究发现，基于SPA理论的定量评价，不仅能够评价一名学生在物理学科核心素养某个维度的达成情况，也能从多个维度甚至是整体上评价多名学生的物理学科核心素养；再者，SPA理论在评价被测对象之后，还能对下次评测情况进行有效的预测.SPA理论下的定量评价，由于其具有的全面性、针对性和预测性等优点，有望在中学物理教学中得到广泛推广.