基于B方法的轨道交通控制系统配置数据的形式化验证

程 鹏，王恪铭, ，王 峥，姚文华，韩 程,

（1．西南交通大学系统可信性自动验证国家地方联合工程实验室，成都 610031；2．西南交通大学计算机与人工智能学院，成都 614202；3．北京全路通信信号研究设计院集团有限公司，北京 100070；4．通号粤港澳(广州)交通科技有限公司，广州 511400）

1 概述

在轨道交通运输业中，轨道交通控制系统[1]的作用类似于神经中枢，其正常运行依赖于正确的配置数据，使用有效方法保证轨道交通控制系统配置数据的正确性十分必要。在目前的实践应用中，对配置数据的验证方式着重于如下两种手段。

1）静态检测

根据数据的编写特征进行扫描，对数据进行静态检测。

优点：运行速度快，可较好地发现数据的完整性问题，如是否空值、长度与结构是否完整等。

缺点：需要人工设计检查规则和检查办法，通过代码的形式，编写专用工具实现检查过程，忽略了如果需要修改或扩充规则，就需要重新修改软件代码，而使得工具的可扩展性和可维护性不强，即编写和修改规则不灵活。

2）功能测试

对数据进行功能性测试，依据设计规范，检查数据流在系统中是否触发相应的操作。

优点：测试过程直观，可发现数据错误导致的问题等。

缺点：严重依赖于测试案例的完整程度和覆盖面，很难遍历所有数据及其组合情况。

综上所述，在目前的研究应用中，更需要找到一种灵活性好、安全可靠性高的方法，即形式化方法[2]。形式化方法是基于严格数学基础，对计算机软件系统进行描述、开发和验证的技术。该方法能够基于形式规约语言，建立系统数据静态规则原型，使用逻辑验证方法，穷尽数据集，验证所有数据及其组合情况是否满足所定义的规则，从而检查数据的完整性和正确性。近10年来，使用形式化方法实现对配置数据的正确性验证，受到了国内外研究者的关注，特别是使用基于一阶逻辑和集合论基础的B方法实现对配置数据的正确性验证。

文献[3-4]展示了自2009年来，各家世界信号行业巨头厂商阿尔斯通(Alstom)、泰雷兹(Thales)、西门子(Siemens)和ProB[5]开发团队以及Atelier B建模平台合作，实现世界各地地铁线路配置数据的形式化验证的工业应用。

文献[6-8]描述英国纽卡斯尔大学的形式化开发小组开发SafeCap铁路站场拓扑形式化设计验证平台，其内部机制是利用Eclipse Modeling Framework, 定义各个铁路站场型信号设备数据的数据结构。通过利用Eclipse开发环境，生成各个信号设备数据，并在该平台内部定义数据静态规则，通过支持将数据及其规则转换为B机器文件格式的脚本，结合ProB模型检验器，实现全自动化判定数据是否满足所定义的规则。

文献[9]对CTCS-1级列控系统线路数据进行形式化验证，其过程也类似。首先需要定义数据所需满足的静态规则，然后使用NUSMV模型检验器实现数据验证。

上述文献聚焦于高铁、地铁、磁浮拓扑线路配置数据的形式化验证技术路线的实现上，与本文不同之处在于研究应用对象不同，本文的应用案例为城市轨道交通列车控制系统[10]配置数据的形式化验证。

轨道交通控制系统作为一类安全苛求系统，任何潜在的系统缺陷都可能会给行车运营安全带来巨大风险。因此，基于各个控制系统配置数据的数据结构，定义配置数据需要满足的规则，使用B语言，将已生成的各个配置数据和定义好的规则形式化，以建立配置数据的静态规则模型，利用ProB模型检验工具验证静态规则模型，从而验证所有的配置数据及其组合情况是否满足给定的规则，以达到验证配置数据正确性的目的。同时，使用形式化语言对规则进行定义时，能够灵活的修改、扩充规则。

2 配置数据的数据结构

以一个实际的城市轨道交通[11]站场拓扑的数据为案例，介绍配置数据的数据结构。

如图1所示，这是一个简化的站场拓扑，只考虑站场拓扑中的道岔对象P（P0-Pn），轨道区段对象(简称区段，section)和信号机对象S（S0-Sn），以及所生成的进路对象，为方便后续的验证工作，整个站场拓扑的编号描述如表1所示。

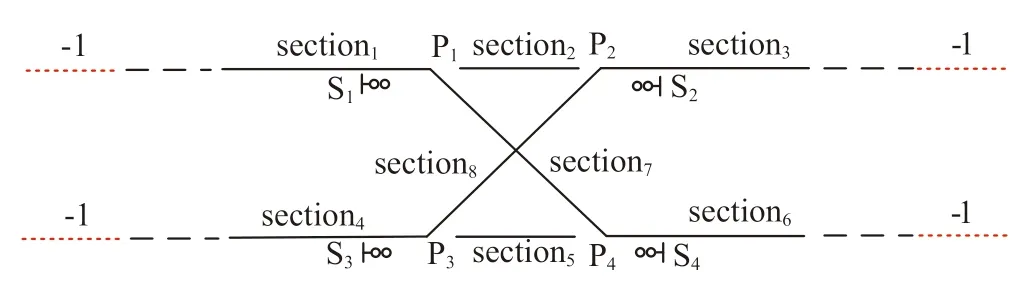
图1 站场拓扑Fig.1 Station topology graph

表1 信号设备对象编号Tab.1 Signaling equipment object number

从图1中可以看出，这些信号设备对象之间存在一定的关系。基于图1给出的简化站场拓扑，给出信号设备对象的数据结构。

2.1 道岔设备数据结构

在本案例的道岔数据结构中，考虑道岔的3种链接关系：第一种是道岔编号和区段编号之间的链接关系；第二种是道岔编号和道岔位置之间的关系；第三种是进路编号和道岔编号之间的关系。道岔编号和区段编号之间的链接关系如图2所示。

图2 道岔编号Fig.2 Turnout number

图2中，P1为道岔编号，section0、section1、section2为区段编号，section0是P1的岔尖区段编号，section1是P1的定位区段编号，section2是P1的反位区段编号。

对于道岔编号和道岔位置间的关系，同进路编号一起组装为一个二次关系，即进路编号-道岔编号-道岔位置。由于每一个进路编号最少有1个道岔编号与之对应，故将进路编号和道岔编号之间的关系组装为一个二次关系，即进路编号-道岔序号-道岔编号，道岔序号可以记录该进路编号有多少个道岔编号。

2.2 区段设备数据结构

在本案例的区段数据结构中，考虑区段有6种链接关系，取图1中的区段编号section1，section1的6种链接关系，如图3所示。

图3 区段设备数据关系Fig.3 Section equipment data relationships

2.3 信号机设备数据结构

在本案例的信号机数据结构中，考虑信号机编号和区段编号之间的两种关系。每一条进路都有一个始端信号机，而在图1中可以看出，每一个始端信号机都对应一个区段。

2.4 进路数据关系

基于上文分析，进路数据共有3种链接关系，分别是进路编号-道岔序号-道岔编号、进路编号-道岔编号-道岔位置和进路编号-信号机编号。除这3种关系外，本案例还考虑进路编号-进路方向编号关系。

3 配置数据需要满足规则的自然语言描述

根据道岔设备、区段、信号机数据结构的定义可知，进路数据关系与这些数据结构有关。本文只对进路数据需要满足的规则进行自然语言的描述。设计3种类型的规则，以验证进路数据的正确性，这3种规则分别有如下验证目的：1）判断进路编号所对应的信号机编号，该信号机编号所对应的区段编号是否通过道岔设备和区段设备数据关系推理得到的区段编号一致；2）判断进路编号中的道岔编号是否正确，即进路编号中的道岔编号是相邻的；3）判断进路编号对应的进路方向编号是否和通过道岔设备和区段设备数据关系推理得到的进路方向编号一致。如表2所示，规则1-6的进路数据满足第一种类型规则，且将进路编号-进路方向编号的完整性规则包含在内。规则7-8的进路数据满足第二种类型规则。规则9-10的进路数据满足第三种类型规则。

表2 进路数据需要满足的3种类型规则Tab.2 Three types of rules to be met by route data

对于第二种类型的规则，进路的道岔编号相邻连续指的是在物理世界里相邻连续，换言之，列车完整通过该进路时，物理空间所经过的道岔编号和数据中的道岔编号是一致的。如图4所示，就是进路中道岔编号不连续的情况，该进路编号包含道岔编号P1和道岔编号P2以及4个互不相同的区段编号，正确的情况是经过依次区段编号section1至section4，但实际却经过如图4虚线所示的部分，因此该进路的道岔编号不是相邻连续的。

图4 进路和区段数据关系Fig.4 Data relationship between route and section

如图5（a）所示，当某进路只经过1个道岔时，由道岔设备的数据结构决定，可以推断出该进路的区段编号一定相邻且连续。

当任意2个道岔编号所连接的4个区段编号出现重叠时，如图5（b）所示，道岔编号P1和道岔编号P2存在相同的区段编号section2，这种情况也一定相邻且连续。

图5 进路和道岔数据关系Fig.5 Data relationship between route and turnout

4 配置数据及其需要满足规则的形式化定义

4.1 B方法介绍

基于本节第2、3节内容和B方法规则[12]，完成配置数据及其规则的形式化定义。一个完整的B开发相当于生成一个B项目，一个B项目包含很多B模块。每一个B模块由一些B组件构成，这些B组件包含3种类型：B抽象机器、B精化机器和B实现机器3种。本文在抽象机器中实现对规则的形式化定义。集合论和一阶逻辑赋予B方法精确的定义和严格的规范形式。

4.2 配置数据的形式化定义

对于已生成数据的形式化考虑两种形式化表达：1）针对各个信号设备对象，分别定义不同的抽象数据类型，每一种抽象数据类型都用一种抽象集合来指代，根据信号设备对象的编号，实例化抽象集合，每一个编号都是一个集合元素。2）针对各个信号设备对象的数据关系，分别定义不同的常量，而后对常量赋值。

1）针对各个信号设备对象的形式化定义

道岔对象的抽象数据类型定义为POINT的抽象集合，实例化后，得到P1至Pn的道岔编号，n为正整数，如公式（1）所示。

信号机对象的抽象数据类型定义为SIGNAL的抽象集合，实例化后，得到S1至Sn的信号机编号，n为正整数，如公式（2）所示。

进路对象的抽象数据类型定义为ROUTE的抽象集合。实例化后，得到R1至Rn的进路编号，n为正整数，如公式（3）所示。

由于区段编号需要划分为4种类型，比如左链接为区段编号、右链接为道岔编号等4种类型，故区段设备的形式化定义使用常量赋值。

2）针对各个信号设备数据关系的形式化定义

道岔设备的数据结构考虑3种链接关系，第一种是进路与道岔的关系，即进路编号-道岔序号-道岔编号，定义常量ROUTE_POINT表示这种关系，该常量的赋值如公式（4）所示，n为正整数。

第二种是进路、道岔和道岔位置的关系，即进路编号-道岔编号-道岔位置，道岔位置反位用0表示，定位用1表示，定义常量ROUTE_POINT_POS表示这种关系，该常量的赋值如公式（5）所示，其中n为正整数，p为0或1。

第三种是道岔与区段的链接关系，为了简化链接关系复杂度，分为道岔编号-岔尖编号-定位编号和道岔编号-岔尖编号-反位编号两种情况，这两种情况的道岔编号相同。分别定义常量point_left_link和point_right_link表示。这两个常量的赋值如公式（6）所示，其中n为正整数，sec1，sec2，sec3，sect4，sec5，sec6为任取的区段编号，sec1和sec3是岔尖编号，sec2和sec4是定位编号，sec5和sec6是反位编号。

区段设备的数据结构考虑6种链接关系。将左链接为尽头、右链接为区段编号的关系，左链接为区段编号、右链接为尽头的关系，以及左右链接均为区段编号的关系，合并为左右链接均为区段编号关系。合并之后，就只有4种链接关系，分别定义常量section_all_section表示左右链接均为区段编号的区段编号链接关系，section_left_section左链接为区段编号、右链接为道岔编号的区段编号链接关系，section_right_section表示左链接为道岔编号、右链接为区段编号的区段编号链接关系，section_null_section表示左右链接均为道岔编号的区段编号链接关系。对这4个常量赋值如公式（7）所示，seca，secd为任意的区段编号，secb，secc，sece，secf为任意的区段编号或尽头，pointa，pointb，pointc，pointd为任意的道岔编号。

根据信号机设备数据结构的定义，考虑信号机的两种链接关系，进路编号-信号机编号和信号机编号-区段编号，分别用常量ROUTE_SINGAL和SIGNAL-SECTION记录，对这两个常量的赋值如公式（8）所示，n为正整数，Sa，Sb为任意的信号机编号，seca，secb为任意的区段编号。

除了道岔、区段、信号机设备的数据关系外，本案例还考虑了进路编号-进路方向编号关系，定义常量ROUTE_DIRECTION来记录，进路方向编号只有0或1，该常量赋值如公式（9）所示，a和b为0或1。

4.3 配置数据需要满足规则的形式化定义

在完成已生成的数据对象形式化后，这个阶段需要考虑之前定义的数据所要满足的规则形式化。这个过程简单描述为，将每一条自然语言的规则描述为具有逻辑真假性的谓词表达式，其判定问题属于约束可满足求解问题。约束可满足问题(Constraint Satisfaction Problem，CSP )[13]的定义是，它由一个三元组组成，其中X是变量的集合，D是变量的取值域，C是约束的结合，X中的每一个变量都对应D中的一个取值域，C中的每一个约束都是由X的子集和一个不相容赋值集合组成。这里的变量集合X可以看成是道岔、信号机、区段设备对象、道岔、信号机、区段设备数据结构包含的关系。取值域D为这些信号设备对象所定义的抽象集合的实例化、其数据结构所定义的常量的赋值如公式（10）所示。

每一个约束C就是一个自然语言描述的规则，这个规则包含部分信号设备对象的描述，对应变量集合X的子集。一般情况下，一个CSP的求解是一个NP-完全问题。若求解的逻辑值为真，则可说明数据满足所定义的规则。反之则不满足。

进路数据需要满足的规则，根据第3节分析，进路数据需要满足的规则除了进路编号-进路方向编号外，分为3种类型，这3种类型定义了8种规则，从规则编号3至规则编号10。

首先，如公式（11）所示给出规则编号1和规则编号2的形式化表达式。

1）第一种类型规则

在规则编号3的描述中，需要基于道岔设备、区段设备数据结构的定义，来获取某进路编号所对应的第一个区段编号，在本案例站场拓扑结构中，进路编号的第一区段编号分为如图6所示的3种情况。

图6 规则编号3的三种情况Fig.6 Three cases of rule number 3

如图6所示，由于这类规则描述过于复杂，为简化形式化表达，特定义道岔位置和道岔数据结构之间的关系，用常量point_link表示，其赋值情况如公式（12）所示。

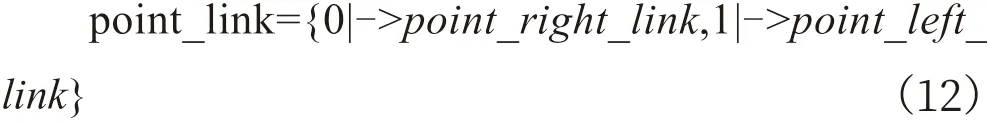
道岔位置处于反位由0表示，道岔位置在定位由1表示，point_right_link和point_left_link为之前定义的常量。有了以上的铺垫说明之后，由于规则编号4和规则编号3是一种类型，现给出规则编号3的形式化表达式，如图7所示。

图7 规则编号3的形式化Fig.7 Formalization of rule number 3

在规则编号3的形式化表达中，量词xx表示进路编号，量词bb表示xx的第一个道岔编号的岔尖区段编号，量词cc表示xx的第一个道岔编号的定位或反位区段编号，具体是定位、反位区段编号，取决于xx。由于考虑进路方向是0，在本案例的站场拓扑中，方向是从右到左，因而bb和cc究竟谁是xx的信号机编号所对应的区段编号，取决于bb和cc谁是左链接为道岔编号、右链接为区段编号的区段编号。若bb是，那么cc一定不会是，因为cc的右链接一定是道岔编号，这是由站场拓扑结构所决定的。反之亦然。规则编号5、6和规则编号3、4类似。

2）第二种类型规则

规则编号7和规则编号8属于第二种类型规则，如图8所示给出规则编号7的形式化表达式。

图8 规则编号7的形式化Fig.8 Formalization of rule number 7

在规则编号7的形式化中，量词xx表示进路编号，由于对xx所包含的道岔进行了排序，量词yy表示xx所包含的除最后一个序号的道岔编号。bb表示区段编号，在任意两个有序的道岔编号中，量词bb是排序靠前的道岔编号的岔尖区段编号，量词cc表示排序靠前的道岔编号的定位或反位的区段编号，是定位还是反位取决于该条进路编号。量词dd表示区段编号，在任意两个有序的道岔编号中，dd是排序靠后的道岔编号的岔尖区段编号。量词ee表示排序靠后的道岔编号的定位或反位的区段编号，和cc一样，也取决于进路编号。由于要满足bb,cc,dd,ee互不相同，而再由站场拓扑道岔数据结构所决定，所以如果bb,cc,dd,ee是连续的，那么集合{bb,cc}中任意一个元素一定与集合{dd,ee}中任意一个元素相邻，因此集合{bb,cc}中一定有一个元素，即，该区段编号一定是左链接为区段编号、右链接为道岔编号的数据结构，且该区段编号的左链接区段编号一定是dd或ee。

3）第三种类型规则

在第一种和第二种类型规则中，其整个形式化表达式的前件，都有使用谓词表达进路方向。而根据霍尔逻辑，前件中所有谓词的布尔值若为假，那么整个表达式为真，因此需要将进路编号所对应的进路方向编号描述在后件中，以验证进路方向编号是否正确，故引入第三种类型规则，编号10与编号9的表达类似。如图9所示，给出了规则编号9形式化表达。

图9 规则编号9的形式化Fig.9 Formalization of rule number 9

在规则编号9的形式化中，量词xx表示进路编号，yy表示区段编号，在xx包含的所有道岔编号中，顺序为第一个道岔编号，其岔尖区段编号为yy，量词zz表示区段编号，是第一个道岔编号的定位或反位区段编号，其定、反位取决于xx。根据站场拓扑结构，进路方向为0的进路编号，其包含的第一个区段编号一定是左链接为道岔编号、右链接为区段编号，根据此性质，验证了进路编号-进路方向编号数据。

5 配置数据的形式化验证

5.1 验证原理

在本文第4节中，定义了很多数据需要满足的规则，对每一个规则的验证都可以看作一个约束可满足求解，每一个规则的形式化表达式可抽象为如公式（13）所示的表达式

公式（13）中，A1，B1是谓词，故蕴含符号的前件可由n个谓词表达式组成，后件也可由n个谓词表达式组成，n为正整数。对这样一个形式化表达式的求解，可转化为如公式（14）所示的表达式。

表达式F的数学逻辑意义为析取范式F，故对形式化表达式的逻辑真假值的求解就转化为对析取范式F的逻辑真假值的求解，这就是自动化约束求解工具的内部求解原理。本文选取的ProB模型检验器(也是约束求解器)，将每一个规则的形式化表达式中的关键量词实例化，实例化后的量词，会给出析取范式的真假值，这样可进一步准确分析错误源，进而修正错误。

5.2 验证结果及分析

将本文表1实例化后，信号对象如表3所示。

表3 实例化后的表1Tab.3 Instantiated table 1

表3给出本实际案例中的各个信号设备对象的个数，本案例共描述49个形式化表达式，在ProB 1.9.3版本运行结束后，验证报错。经过检查，错误进路编号-信号机编号27-64中，信号机编号为24，27，30号所对应的区段编号有错误，与现场数据设计人员反馈后，实际情况是在验证规则中没有考虑到区段偏移。

修正后，再次运行验证，又发现错误，如图10所示。经过检查，发现在Excel表中编写的进路编号-进路方向编号中的进路方向编号有误，与现场数据设计人员反馈后，实际上1-27号进路还没有开通，进路编号为14-16所对应的进路方向编号有误。

图10 进路方向编号有误Fig.10 The route direction number is incorrect

修正后再次运行验证，结束后，如图11所示，没有再发现错误。验证所有的形式化表达式的逻辑值都为真，至此，数据的静态正确性检测已完成。

图11 正确的验证结果Fig.11 Correct verification results

5.3 验证小结

基于本文的设计、定义、验证、分析过程，总结数据的形式化验证方案有如下优点。

1）验证严谨：使用无歧义的数学逻辑符号描述数据静态规则；

2）规则可维护性和可扩展性好：编写修改灵活，如果更换开发人员，只要理解形式化数学符号，就能看懂规则；

3）验证分析过程的直观性好：利用ProB模型检验器，能够直观的定位到错误的位置；

4）验证成本低：体现在验证速度非常快。

6 结论

本文以轨道交通控制系统配置数据为例，基于B方法建立配置数据静态规则原型，并进行形式化验证。本方法有助于发现并纠正轨道交通控制系统配置数据存在的错误，减少因配置数据错误而引发系统缺陷，验证后的配置数据可以作为系统正常运行的基础，减少了数据测试阶段的成本投入。未来的研究方向可以考虑针对数据关系更为复杂的配置数据，研究基于一阶逻辑和集合论的B语言如何实现对其的描述，以及考虑更多场景的应用。