金属结构临时作业棚抗冲击能力分析

张宇

0 引言

工作人员为了深入分析金属结构临时作业棚抗冲击能力，通过建立木材弹性本构方程以及损伤演化模型，得到木材本构关系模型。并基于ABAQUS 软件的通用分析模块与显示分析模块，创建材料子程序并进行验证，在获得临时作业棚主要材料性能参数之后，建立临时作业棚有限元结构模型，模拟高空坠物对临时作业棚各个部位所造成的冲击，为提升金属结构临时作业棚抗冲击能力提供数据基础。

1 建立木材本构模型

从类型上看，木材属于各向异性材质，当木材受到拉力、剪力时会出现脆性破坏现象，当木材受到压力则会发生延性破坏。当木材受到冲击力之后，其各个方向上的拉力屈服强度、压力屈服强度会存在很大差异。因此，设计人员根据金属结构临时作业棚顶部木材的特点，创建木材本构模型（如图1所示）。

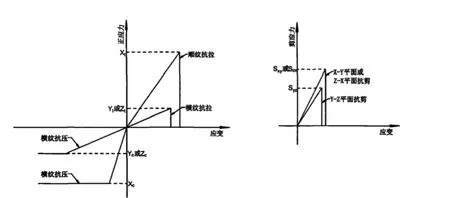
图1 木材本构模型

通过分析图1 可以看出，X与X为沿着木材纹理方向的抗压、拉屈服强度，Z、Z则为木材横纹切向抗压、拉屈服强度，Y、Y为木材横纹径向抗压、拉屈服轻度，S、S以及S分别为木材三个平面的抗剪强度。

1.1 木材应力应变关系式

为了方便计算，设计人员将各向异性转变为正交各向异性，通过转化可以确定木材的应力－应变关系：

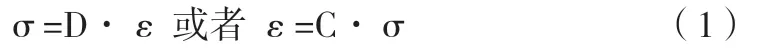
公式（1）中，变量σ 代表应力矩阵，常量C 与D 分别代表木材的柔度矩阵以及刚度矩阵，变量ε 代表木材的应变矩阵。将公式σ=D·ε转化为矩阵，可以更好地观察应力应变关系变化。

1.2 构建损伤演化模型

构建损伤演化模型的主要目的是如果材料出现的损伤，可以根据该模型分析材料的弹性模量以及强度等关键指标的动态响应情况。该模型以CDM 作为理论基础，当材料受损之后其柔度矩阵与刚度矩阵呈非线性变化特点。

由于木材属于各向异性材质，需要使用各向异性屈服准则，才能够对木材受损情况进行预判。经过众多科研人员的研究，终于在Sun 与Yamdad 的带领下，提出Yamada-Sun 屈服准则。该准则认为木材各个轴上的强度相互独立，某一条轴对应两个剪应力以及一个正应力，通过计算正应力与剪应力数据，就能确定木材的屈服强度。

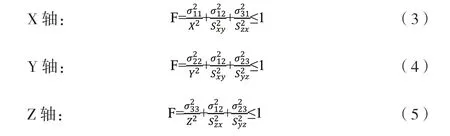
公式（3）（4）（5）中，F 为木材的屈服系数，X、Y、Z则分别代表木材在三个方向上的抗压强度，依据不同的应力状态（σ、σ、σ），选择对应的抗压强度或者抗拉强度。根据该标准判定木材在受到冲击之后，各个轴是否屈服。x、y、z 代表木材在抗冲击实验中的三个方向，分别为顺纹纵向（L），横纹切向（T）以及横纹径向（R）。

2 ABAQUS 程序设计

ABAQUS 系统主要由显示分析模块以及通用分析模块两个部分组成，前者在准静态分析中较为常用，后者在静力分析中较为常见。在运用两组模块进行力学分析时，需要在确保惯性力较小的状态下，用最短的时间进行冲击模拟，例如冲切以及碰撞等。本次设计中，考虑到高空坠物对于木方的冲击以准静态分析为主，因此选择使用显示分析模块模拟高空坠物的冲击数据。

ABAQUS 系统为用户提供了大量的材料本构模型以及单元库，能够模拟大多数材料受到冲击之后的形变数据。但是该系统的局限性在于无法直接调用材料本构模型进行实验，需要借助二次开发平台，依据实际情况对材料本构模型进行自定义设计。本次实验中，工作人员使用Fortran 编译器对木材的本构模型进行自定义编辑，并利用Vumat 程序检查本构模型是否存在错误。相关工作人员在该程序中输入了21 种材料参数，并对其状态变量进行定义，定义数量达到16 个（详见表1）。

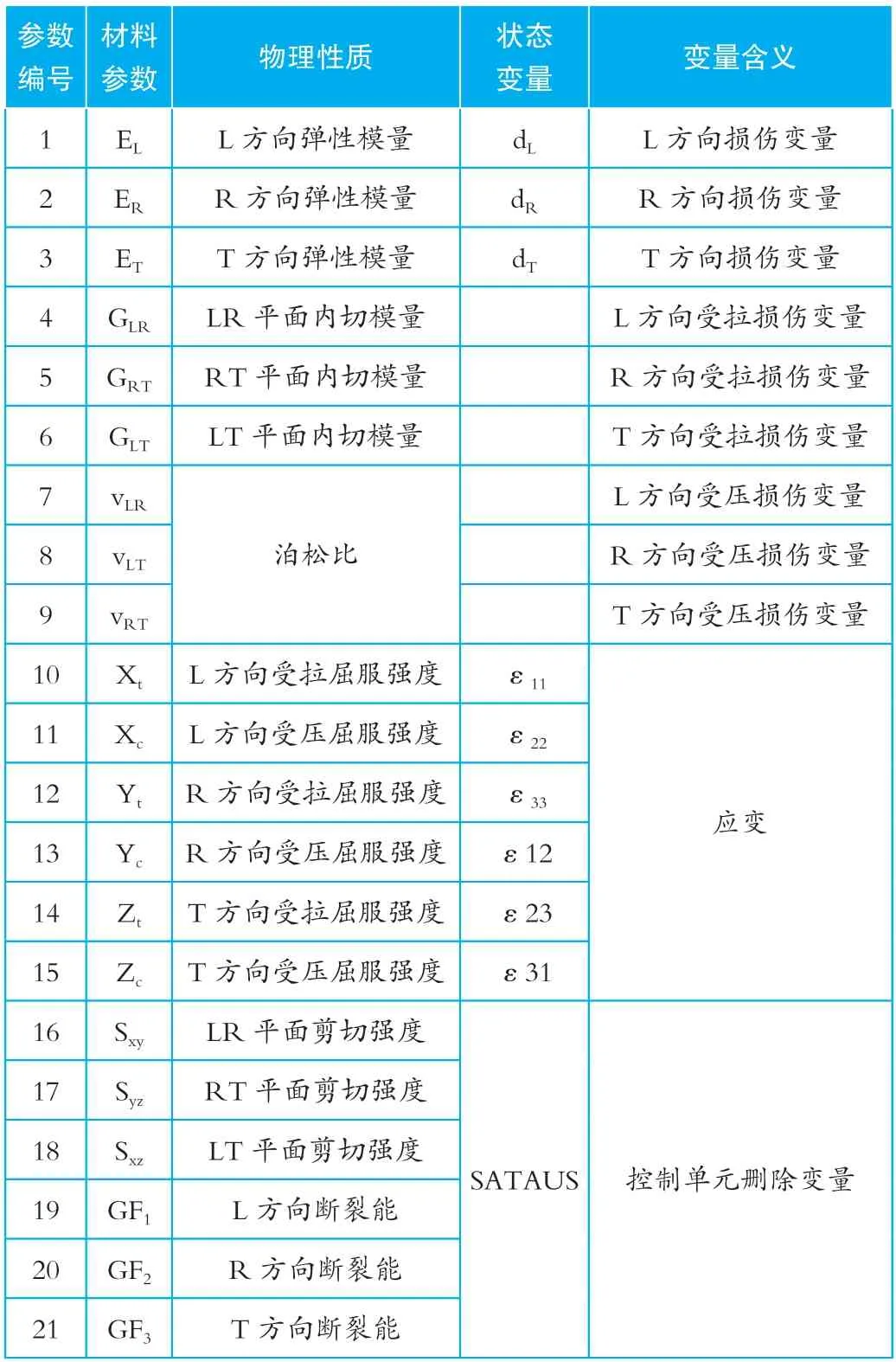
表1 VUMAT 材料常数

3 金属结构性能参数计算

金属结构临时作业棚中的金属结构以钢材为主，本次试验中用到的钢材为Q235 薄壁型钢，尽管钢材受到的冲击力属于间接受力，是瞬态作用过程，但仍处于动力学范畴之内。因此在对材料进行定义的过程中，仍然需要加入应变率。设计人员根据Cower-Symonds 模型对钢结构应变效率进行定义。

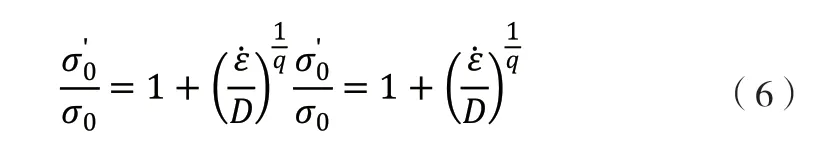
公式（6）中，σ表示钢材的静力强度，则表示钢材在不同的塑性应变率（ε）下的动态强度数据。变量D 与q 均为计算参数，依据材料类型的不同，D 与q 也会发生变化。本次设计中，考虑到临时作业棚钢结构与碳素钢的应变率相仿，因此将D 设定为40，q 为5 即可（详见表2）。

表2 钢材料性能参数

本次试验中用到的临时防护棚以木材作为主要材料构成顶端防护层，考虑到施工成本因素，以就地取材为原则，选择木方与木模板作为防护层木材。木方使用花旗松，木模板采用杨木LVL。

4 建立有限元模型

4.1 施加约束力

金属材料施工临时作业棚所使用的钢管，使用固接法进行连接，实验中模拟高空坠物与作业棚的接触点，仅需要计算垂直方向的位移数据，其他方向数据均设定为0。临时作业棚上方设计有横向空腹式防护结构，防护结构内部布置的木方以及木质模板，边界条件选择为开放状态，并在高空坠物与作业棚接触点，施加一个竖直方向的初始速度。

4.2 划分网格

由于临时施工棚使用的钢材数量较多，且钢材体积较大，因此使用S4R 网格进行建模。在实验过程中，为了提升计算效率，可以将高空坠物简化为一个离散刚体，在接触到作业棚之后不会发生变形，其与作业棚只存在一个接触点，该接触点即为参考点，运用壳单元模型对刚性单元进行建模。针对作业棚中的木材，使用实体单元进行建模，并在计算机中构建3D 坐标系，对于木材的横纹切向、横纹径向以及顺纹进行标定，对应3D 坐标系中的Y、Z、X 轴。运用结构化划分方式对木材进行网格化处理，利用8 节点线性缩减积分构建C3D8R 实体单元模型。

4.3 接触分析

构建临时施工棚有限元模型的主要目的，是计算高空坠物、钢部件、木材之间的相互作用力。为了方便结算，该模型中的钢部件使用Tie 型接触进行约束，高空坠物与参考点之间使用coupling 约束条件，高空坠物与木方、钢结构桁架之间采用Surface tu Surface 接触模式，模型的切向使用库伦摩擦，将摩擦系数设定为0.3。由于本次实验中将高空坠物设定为离散刚体，木材的刚度小于高空坠物，因此将高空坠物设定为主面，木方与横向空腹式桁架相比，其刚度较小，因此将横向空腹式桁架作为另一个主面（如图2 所示）。

图2 临时作业棚抗冲击有限元模型

5 临时作业棚抗冲击性能分析

在分析临时作业棚抗冲击有限元时，要确保高空坠物在下落过程中其质量与形状不发生变化。其坠落高度与冲击性等价，作业棚受到冲击之后其中心位置发生的形变最为明显。因此，设计人员运用AVAQUS 软件中的显示分析模块建立抗冲击有限元模型，该模型一共44 个，能够从木材厚度、冲击力作用面积等方面验证作业棚抗冲击能力。

对于44 个有限元模型的抗冲击能力进行分析之后，得到临时作业棚横向空腹式桁架以及木方的最大冲击力，Mises 应力以及木方的破坏面积数据。

5.1 作用面积对临时作业棚抗冲击能力的影响

如果在金属材料临时作业棚顶端的横向空腹式桁架内布置杨木LVL 或者花旗木，其作用面积与冲击力有限元分析结果如下（如图3 所示）。

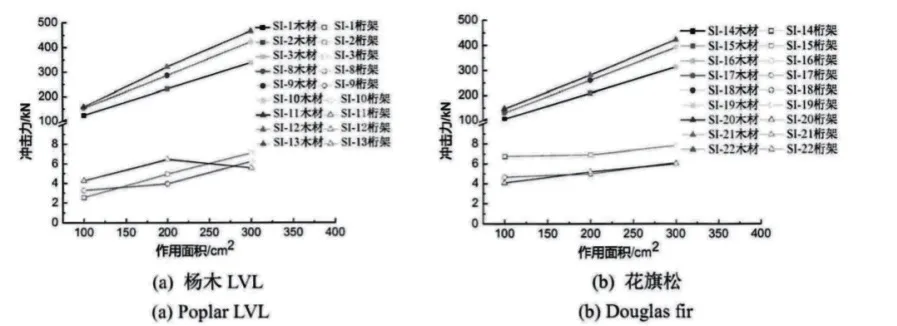
图3 杨木LVL、花旗木作用面积与冲击力有限元分析

通过分析图3 可以发现：杨木LVL 在受到冲击力之后，与坠物的接触面积越大，其冲击力越大。随着作用面积扩大，在冲击能量不变的情况下，杨木LVL 的位移与接触面积呈反比例关系，作用面积越大杨木LVL 位移越小。木材位移的减少，意味着横向空腹式桁架所受到的冲击力变大，其位移增加。这种状态下，杨木LVL 与桁架的Mises 应力以及破坏面积，也会随着接触面积增大而加大，冲击造成的破坏以顺纹剪切破坏为主。

如果将杨木LVL 替换为花旗松，冲击作用面积越大，花旗木与桁架位移、Mises 应力变化越大。但由于花旗木厚度较大，具有很好的刚度，因此在受到冲击力之后，高空坠落的物体会向反方向反弹，因此对于桁架的作用时间较短，桁架的位移变小。这种情况下，高空坠物对于木方的破坏以横纹径向破坏为主。

5.2 坠落高度对临时作业棚抗冲击能力影响

临时作业棚横向空腹式桁架中布置杨木LVL 或者花旗松木方，其作用面积与位移的有限元分析如下（如图4 所示）。

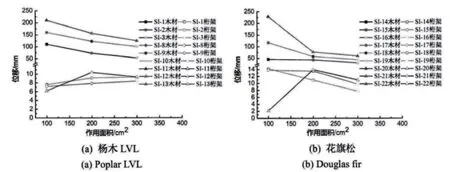
图4 杨木LVL、花旗木作用面积与位移的有限元分析

通过分析图4 可以发现：坠落高度越高，桁架与木方受到的冲击力越大，木方的位移也越大。由于木材受到外力作用出现变形之后，对于高空坠物会起到一定的缓冲，因此坠物对于桁架的影响相对较小，桁架的位移也会逐渐减少。当坠物的高度较低，木方受到的破坏以顺纹纵向剪切为主。如果坠物位置较高，则木材会彻底断裂。

坠落物高度越高，花旗松木方移动越大，Mises 应力与坠落物高度成反比，其原因在于坠落物越高其下落的速度越快，木方受到冲击之后以横纹切向剪力破坏为主，木材吸收了大量的动能，使得桁架结构的位移变小，其受到的冲击力也显著降低，有利于保障桁架结构的完整性。

6 结语

工作人员利用ABAQUS有限元分析软件，对金属结构临时作业棚抗冲击能力进行了深入分析，通过模拟实验分别论证了高空坠物的质量、坠落物高低以及木材厚度的变化以及对于临时作业棚抗冲击能力的影响，计算钢结构、杨木LVL 以及花旗松木方在受到冲击后的Mises应力变化情况、位移情况以及冲击的破坏形式。通过实验研究得出以下结论：

（1）坠落物作用面积越大、高度越高，其对于木方所造成的冲击力越大，位移越明显。同时木材能够吸收的能量也越多，当木材无法抵消冲击力就会被彻底击碎，受到冲击的时间也会相应变短。横向空腹式桁架受到的冲击力、位移以及Mises 应力与坠落物的作用面积、高度成反比关系，作用面积越大，桁架越稳定。

（2）在布置防护层时，可以采用厚度较大的木方，提升木方的刚性，确保木方能够吸收大部分冲击力。也可以采用单体面积较大的木质模板，通过均匀吸收冲击力保证金属结构的安全。在不影响施工进度以及成本的情况下，可以集中二者的优势，选择厚度较大且作用面积大的木方木质模板组合，提升临时作业棚的抗冲击能力。

（3）钢结构桁架在受到冲击之后，变形不明显，没有达到钢构件的屈服强度，整个金属结构体系能够保证安全。