寻找不一样的精彩

范建兵

折叠问题是初中几何的重要内容之一。在四边形这块内容里，我们时常遇到各种特殊四边形中的折叠问题，试着动手叠一叠，发现方法，以此解决不同的问题。

一、矩形中的折叠问题

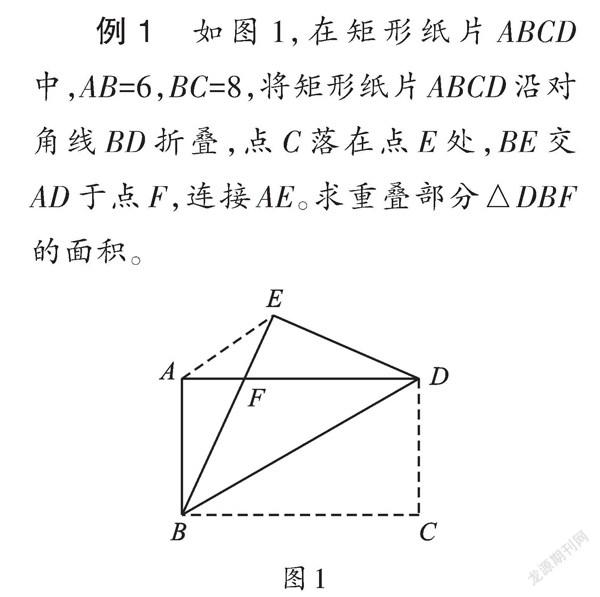
例1 如图1，在矩形纸片ABCD中，AB=6，BC=8，将矩形纸片ABCD沿对角线BD折叠，点C落在点E处，BE交AD于点F，连接AE。求重叠部分△DBF的面积。

【点拨】这是一个大家比较熟悉的折叠状态，解题时需要把握两个关键点：一是确定△DBF的形状，由“折叠+平行”可得△DBF是等腰三角形（也可以借助△ABF≌△EDF证得）;二是计算线段DF的长度，在Rt△AFB中运用勾股定理可求得BF的长，最后再计算△DBF的面积。

二、菱形中的折叠问题

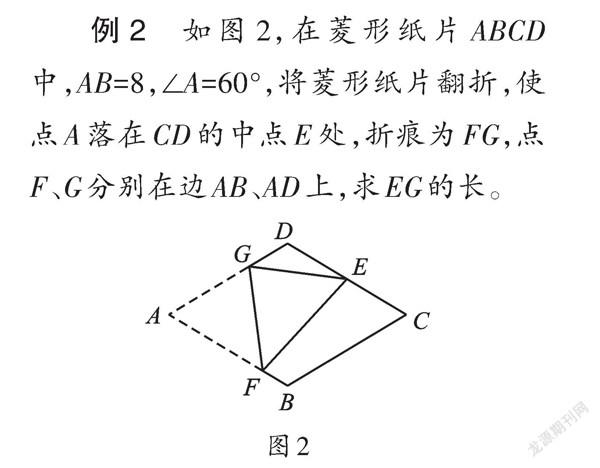
例2 如图2，在菱形纸片ABCD中，AB=8，∠A=60°，将菱形纸片翻折，使点A落在CD的中点E处，折痕为FG，点F、G分别在边AB、AD上，求EG的长。

【点拨】求线段的长，常用的方法有两种：一种是借助特殊图形直接进行计算，另一种是寻找相等线段进行转换。本题中由折叠可得AG=GE，故要想计算EG或AG的长，最好能够将它们放在一个特殊图形中（如直角三角形等）。因此，可以过点E作EM⊥AD，交AD延长线于点M，构造出含有EG边的直角三角形，再根据勾股定理计算得出相应线段的长。

三、正方形中的折叠问题

例3 如图3，M、N分别在正方形ABCD的边AD、BC上，将正方形沿MN折叠后，点D落在边AB上的D'处，C落在C'处，连接DD'。

（1）求证：∠AD'D=∠DMN;

（2）若AD=6，AD'=2，求折痕MN的长。

【点拨】（1）由折叠性质知MN⊥DD'，又因为∠A=90°，所以∠ADD'与∠DMN互余，∠ADD'与∠AD'D互余，所以∠DMN=∠AD'D;（2）所求折痕MN的长，其实就是线段DD'的长。过点N作NE⊥AD于点E，容易证明△ENM≌△ADD'，从而MN=DD'。而DD'的长可以在Rt△ADD'中根据勾股定理求出。

从上面的三个例题可以发现，折叠问题的融合性强，不仅考查了轴对称的性质，还考查了特殊图形（如矩形、菱形、正方形）的性质、全等三角形的判定与性质、直角三角形的性质、勾股定理等。解决折叠问题，我们需要处理好以下两个难点。

一是识图难。结合题意看懂图形、理解图形是解决此类问题的关键要素。折叠问题中的图形往往呈现给我们的是“叠”的结果，而没有“折”的过程。因此，大家不妨动手试试，先在动态的折叠过程中感受折叠的变化，观察变与不变，然后思考其中蘊含的相关性质，最后再考虑折叠结果中的问题。在动态的折叠中思考静态的结果，寻找熟悉的、常用的解题模型，合理地理解图形、分析图形。

二是计算难。计算的前提是知道算什么和怎么算。因此，在解决折叠问题时常常需要思考以下问题：（1）以什么为轴进行折叠;（2）折叠前后边或角的数量关系;（3）折叠是否产生了新的特殊图形，如等腰三角形、直角三角形等;（4）要计算的线段或角，在哪些图形中可以求得，怎样求更合理。实践中我们发现如下规律：折叠常伴等腰，这便于我们在解决问题中快速寻找相等的线段或角;折叠常用勾股，这便于我们在计算中更方便、更快捷、更合理。

（作者单位：苏州高新区景山实验初级中学校）