基于CSO-SVR的低压架空线路谐波损耗评估

孟安波， 蔡涌烽， 符嘉晋， 陈德， 殷豪， 陈子辉

(1. 广东工业大学自动化学院，广东 广州 510006；2. 广东电网有限责任公司江门供电局，广东 江门 529000)

0 引言

随着我国风电、光伏等新能源发电并网规模的日益增加以及电动汽车等依托新型电力电子器件的负荷日趋增多，谐波污染问题愈发严重且复杂。而直接与诸多用户相连的低压配电网，其线路损耗在各电压等级线路损耗中占比最高[1—2]，其中谐波污染导致的线路损耗不容小觑[3—5]。因此，开展考虑谐波因素的线路损耗研究，对分析线路损耗构成、制定精确节能降损措施具有重要意义。

对于低压架空线路而言，线路损耗主要与电流、电阻有关，围绕谐波电阻建模是谐波损耗研究中的重要环节。现有研究中，文献[6—7]以谐波次数的算术平方根倍直流电阻表征各次谐波电阻；文献[8]基于电磁理论和电流热效应，推导电流密度分布，进而计算谐波电阻；文献[9—10]采用交直流电阻比值法计算谐波电阻；文献[11]提出磁特性分析法计算导线交流电阻。上述方法需要大量的精确参数，且计算精度及方法适用性有待进一步提升。因而寻求更为便捷且精确的谐波损耗评估方法具有一定的工程实用价值。

近年来，人工智能算法飞速发展，相关智能模型如反向传播(back propagation，BP)神经网络[12]、径向基函数(radial basis function，RBF)神经网络[13]、深度置信网络[14]、支持向量回归(support vector regression，SVR)[15]模型等已成功应用于线路损耗评估中。文献[13]利用改进粒子群优化 (particle swarm optimization，PSO) 算法优化RBF神经网络，进而计算线路损耗；文献[14]提出基于深度置信网络的低压台区线路损耗计算方法。但上述研究均未涉及网络层数目确定方法。文献[16]通过十折验证法与试凑法相结合确定最佳网络结构，并利用自遗传算法改进BP神经网络，实例验证表明模型具有较好的收敛能力和泛化性。但上述神经网络面临最优网络结构设计问题，且训练过程中易陷入局部最优。而SVR按照结构风险最小化原则进行建模，通过求解凸二次规划问题获取最优解，具有泛化能力强、全局最优及收敛速度快的显著优点[17—19]，既避免了局部最优问题，又不必进行复杂的神经网络结构设计。对于SVR模型超参数的选取，已有研究采用PSO算法进行动态优化[15]。而纵横交叉优化(crisscross optimization，CSO)算法与PSO算法相比，全局搜索能力更强、收敛性能更好[20]。

因此，文中基于SVR模型评估谐波影响下的线路损耗，以SVR强大的非线性拟合能力自动学习线路特征与谐波损耗之间的关系。同时，利用CSO算法全局搜索能力强、收敛精度高的优点，对SVR超参数进行动态搜索，获取较为合适的参数，进而建立CSO-SVR谐波损耗评估模型。最后，基于国内某大型电能质量综合试验平台，获得低压架空线路谐波损耗实测数据，对所提CSO-SVR谐波损耗评估模型的优越性进行验证。

1 低压架空线路谐波损耗分析

电力系统中线路模型可以分为集中参数模型和分布参数模型，低压配电网中的线路属于短线路，利用线路等值模型进行计算时采用集中参数π型等值电路[1]，如图1所示。

图1 低压架空线路的π型等值电路Fig.1 π-type equivalent circuit oflow-voltage overhead line

图1中，Z=R+jX为低压架空线路等值阻抗，其中R为等值电阻，X为等值电抗;Y/2为等值电纳；UB，UN分别为母线B，N处的电压。计算线路损耗时，长度较短的低压线路损耗近似等于电阻损耗[1]，因此文中计算谐波损耗时不考虑线路电抗及电纳。由谐波叠加效应可知，各次谐波损耗之和等于总谐波损耗。则谐波影响下的架空线路损耗为：

(1)

式中：ΔPhar为考虑谐波因素的低压架空线路损耗；Ih为h次谐波电流；Rh为h次谐波电阻；h=1表示基波分量；H为线路上存在的最高谐波次数。

式(1)中，Ih可由傅里叶变换得到，Ih与谐波频率、线路材质等多种因素相关，计算过程复杂。文中通过物理解析模型计算低压架空线路谐波损耗时，采用文献[6—7]中应用较为广泛的谐波电阻模型。

(2)

式中：b为导体半径；σ为电导率；δc为趋肤深度；ω为谐波频率；μ为导体绝对磁导率。

2 CSO-SVR谐波损耗评估模型

2.1 性能指标

文中选取平均绝对百分比误差(mean absolute percentage error，MAPE)XMAPE、平均绝对误差(mean absolute error，MAE)XMAE、均方根误差(root mean square error，RMSE)XRMSE衡量模型的谐波损耗评估性能。则：

(3)

式中：yi，y′i分别为第i个测试样本的谐波损耗量测值及评估值；S为测试样本数。

2.2 评估流程

基于CSO-SVR的架空线路谐波损耗评估模型应用流程如图2所示，具体步骤如下。

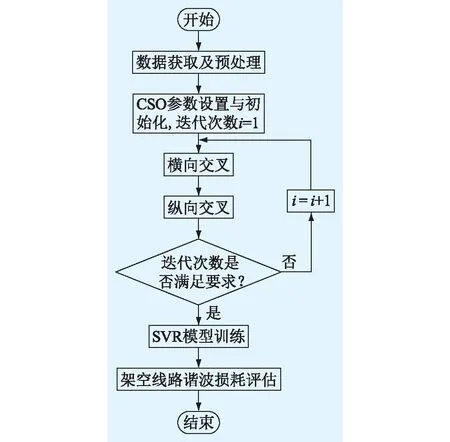
图2 谐波损耗评估流程Fig.2 Evaluation process of harmonic loss

(1) 数据获取及预处理。基于国内某大型电能质量综合试验平台获取架空线路谐波试验数据。对数据进行归一化处理。模型输入包括首端三相基波电压、三相基波电流，末端三相基波电压，平均基波电流以及2～25次平均谐波电流含有率，共34维，模型期望输出为线路谐波损耗。

(2) CSO参数设置与初始化。设置CSO基本参数：种群规模为40；最大迭代次数为50；纵向交叉概率为0.4；随机初始化种群，迭代次数i为1。

(3) 横向交叉。种群粒子两两不重复配对，交叉产生新粒子并计算适应度，进入竞争机制并保留适应度更优的粒子。

(4) 纵向交叉。按照纵向交叉概率选取一定维度的粒子信息，交叉产生新粒子，计算适应度后进入竞争机制。

(5) 迭代判断。若满足最大迭代次数要求，输出最优粒子对应的参数组，否则迭代次数加1并返回步骤(3)。

(6) SVR模型训练。将种群最优粒子对应的超参数代入SVR模型，利用训练集进行训练。

(7) 架空线路损耗评估。将测试集电气特征数据输入CSO-SVR模型，输出谐波损耗评估值。

在上述评估流程中，CSO种群粒子适应度计算及SVR模型训练均使用训练集数据，测试集数据则用于模型有效性验证中。

3 CSO-SVR模型原理与算法

文中采用SVR模型学习线路特征与谐波损耗之间的关系，以全局搜索能力强的CSO算法优化SVR模型的超参数，通过CSO-SVR模型将电压、电流等特征映射到高维空间从而实现线性拟合。输入线路电压、电流、谐波含有率等数据，即可获取对应谐波损耗评估值。

在CSO种群粒子设计时，由SVR模型的超参数组[C,ε,λ]构成单个粒子信息，每个粒子代表超参数的一种组合情况。其适应度函数Ffit和参数范围设置如式(4)所示，其中超参数组[C,ε,λ]的优化范围根据文献[15，21]进行设置。

Ffit=fSVR(C,ε,λ)
C∈[1,200]；ε∈[10-6,0.2]；λ∈[10-2,2]

(4)

式中：C为惩罚参数；ε为不灵敏损失参数；λ为核参数；fSVR(C,ε,λ)为每个粒子信息对应的SVR模型损耗评估值与测量值的XMAPE。

3.1 SVR算法

SVR基于结构风险最小化原则建立回归模型，其核心思想是在样本映射得到的高维空间中求解最优超平面，通过样本与超平面偏差最小化实现回归。最优超平面可以表示为：

f(x)=wφ(x)+b

(5)

式中：x为输入向量；φ(·)为映射函数；w为权值向量；b为阈值。

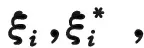
(6)

(7)

式中：m为训练样本总数。

K(xi,xj)=φ(xi)φ(xj)

(8)

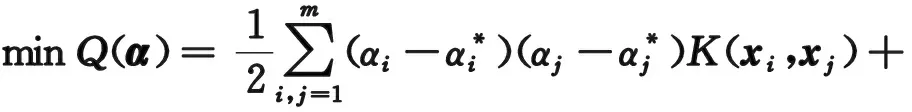
(9)

(10)

求解上述优化问题，得到回归曲线为：

(11)

式中：K(xi,x)为构建SVR模型时选用的RBF核函数[19]。

K(xi,x)=e-λ‖x-xi‖2

(12)

在SVR模型中，将电气特征映射到高维非线性空间，求解对偶优化问题得到回归曲线，可实现未知损耗评估。分析可知，C，ε，λ与回归曲线密切相关，对模型的拟合能力和评估性能影响极大。准确高效地选择这些参数是建立SVR模型的关键。文中使用全局搜索能力强、寻优性能好的CSO算法对SVR超参数进行动态寻优，可有效解决参数确定难的问题。

3.2 CSO算法

CSO算法以横、纵交叉机制结合竞争机制的方式运行[22]。横向交叉赋予算法优秀的全局搜索能力；纵向交叉促使算法跳出局部最优解，获得更好的收敛速度和收敛精度；竞争机制使得算法迭代始终保持最优解，加速收敛。

3.2.1 横向交叉

横向交叉指种群中不同粒子同一维信息的算数交叉，假设父代粒子的第d维信息发生交叉，则新粒子的产生方式为：

(13)

式中：Sh(i,d)，Sh(j,d)为产生的子代粒子，i,j=1,2,…,M，d=1,2,…,D，其中M为种群规模，D为粒子信息维度；X(i,d)，X(j,d)为父代粒子；r1，r2，c1，c2为[0,1]的随机数。

横向交叉时，采用扩展系数c1，c2增大粒子搜索范围，减少搜索盲区，有效提升全局搜索能力。

3.2.2 纵向交叉

纵向交叉指种群同一粒子不同维信息的算数交叉，假设父代粒子第d1维信息X(i,d1)和第d2维信息X(i,d2)发生交叉，产生的子代粒子Sv(i,d1)为：

Sv(i,d1)=rX(i,d1)+(1-r)X(i,d2)

(14)

式中：r为[0,1]的随机数；d1,d2=1,2,…,D；i=1,2,…,M。

纵向交叉利用信息之间的差异引入粒子变异，在提升种群多样性的同时也可以促进陷入局部最优的粒子跳出困境，提升全局收敛能力。

4 案例验证与分析

文中基于380 V低压架空线路谐波试验数据，对CSO-SVR模型的有效性进行验证。线路采用三相四线制接线方式，允许载流量为423 A，电阻为0.164 Ω/km，长度为160 m。

4.1 架空线路谐波试验

电能质量扰动试验平台具有电压/电流扰动调节功能，可真实模拟电网中各类典型电能质量问题，扰动试验原理如图3所示。

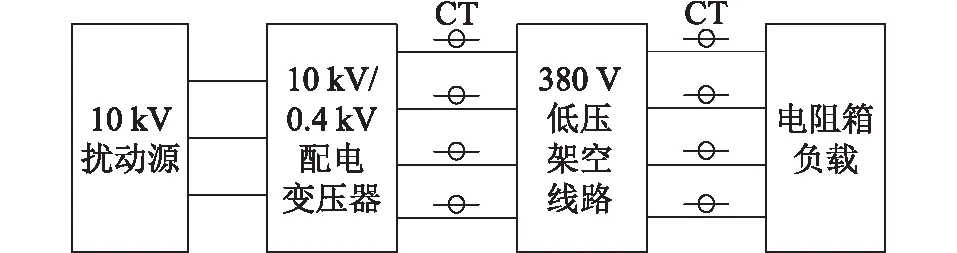
图3 电能质量扰动试验原理Fig.3 Principle of power quality disturbance test

试验时通过配电变压器将谐波电压源转换为380 V，用低压架空线路连接变压器与电阻箱负载。为确保采样精度和采样同步性，通过16通道Synergy录波仪以50 kHz频率同时采集架空线路首、末端电压以及电流数据，其中电流数据来自线路两端的电流互感器(current transformer，CT)。

试验中，架空线路带120 kW电阻负载。控制谐波电压源输出基波分别叠加2～25次单次谐波，谐波含有率为5%～20%，谐波含有率调节步长为5%，共完成96个单次谐波工况试验。由谐波电压源输出基波同时叠加多个谐波的组合，共完成7个组合谐波试验。组合谐波工况如表1所示。

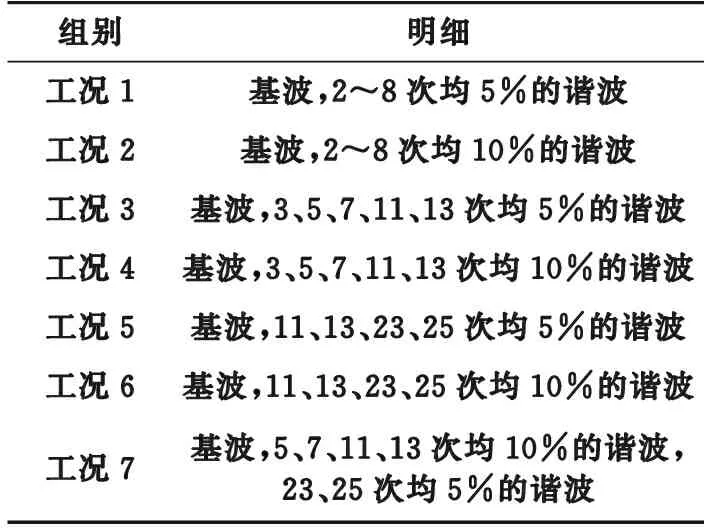
表1 组合谐波工况Table 1 Combined harmonic conditions

4.2 数据处理及划分

将谐波工况试验所得电压电流录波数据进行傅里叶分解处理，得到各个工况下的基波电压、基波电流、谐波含有率和线路损耗等。最后获得单次谐波9 600组数据作为训练集，组合谐波700组数据作为测试集。每组数据包括：架空线路首端三相基波电压，首端三相基波电流，末端三相基波电压、平均基波电流以及2～25次平均谐波电流含有率，线路损耗。

为排除各项参数之间数量级的影响，提高评估模型的可靠性，将数据归一化至[0,1]之间。

(15)

式中：x′为数据x归一化后的值；xmax，xmin分别为x的最大值和最小值。

4.3 模型有效性验证

为了验证文中所提CSO-SVR模型的有效性，分别采用物理解析、BP、RBF、SVR、PSO-SVR、CSO-SVR模型进行对比分析。其中，由PSO、CSO算法动态寻优得到的SVR模型超参数分别为：

(16)

(17)

按表1测试集工况进行划分，谐波损耗的物理解析模型计算值、智能模型评估值以及实际测量值均以平均值表示，见图4。由图4可知，CSO-SVR模型的谐波损耗评估值与实际测量值最为接近，评估性能最好。各模型的谐波损耗评估误差见表2。

图4 谐波损耗对比Fig.4 Comparison of harmonic loss

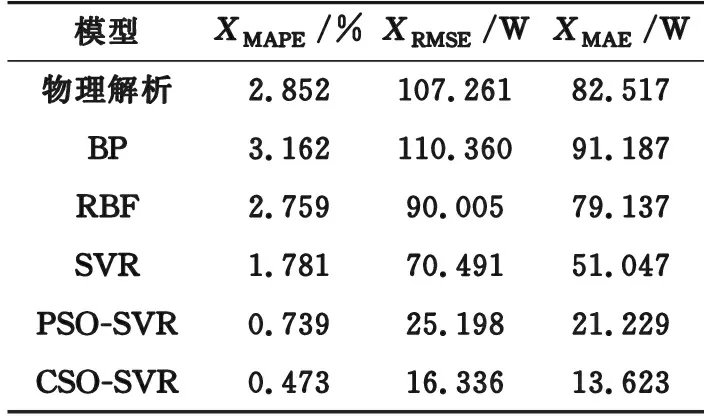
表2 谐波损耗评估误差Table 2 Evaluation error of harmonic loss

分析图4、表2可得：

(1) 物理解析模型在工况1，3，5(单次谐波含量为5%)的谐波损耗评估结果与实测值较为接近，在其他4个工况下(单次谐波含量大于5%)相差较大。物理解析模型的XMAPE为2.852%，其计算精度不高，多用于近似计算。

(2) SVR模型的谐波损耗评估误差小于物理解析、BP和RBF模型。与物理解析模型相比，SVR模型的XMAPE，XRMSE，XMAE分别降低37.553%，34.281%，38.138%。而BP模型各项误差较大，RBF模型评估结果与物理解析计算结果较为接近。这是由于人工神经网络在训练过程中易陷入局部最优，而基于结构风险最小化原则建立的SVR模型可求得全局最优解，且无需复杂的神经网络结构设计。

(3) CSO算法在优化SVR模型超参数方面表现更优。与SVR模型相比，PSO-SVR模型的XMAPE，XRMSE，XMAE分别降低58.506%，64.254%，58.413%。可见，超参数的选取是发挥SVR模型非线性拟合能力的关键，采用动态寻优可有效选取合适的超参数。CSO-SVR模型的XMAPE，XRMSE，XMAE相比PSO-SVR模型分别降低35.995%，35.169%，35.828%。这是由于CSO纵横交叉机制可以使种群在参数寻优中具有比PSO算法更强的全局搜索能力和更好的收敛性能，从而得到更为合适的超参数，进一步提升了模型性能。

此外，对比各模型运算耗时，如表3所示。

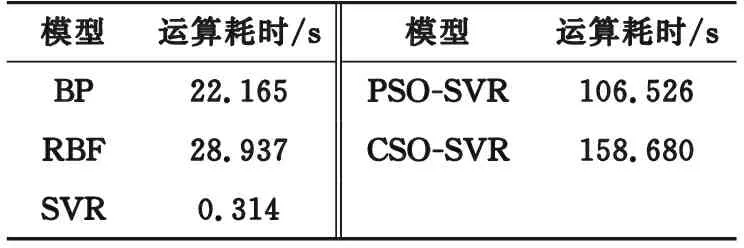
表3 模型运算耗时Table 3 Calculation time of model

由表2、表3可知，BP、RBF神经网络运算耗时均为20 s以上，且其评估误差都较大。SVR模型运算耗时最少，仅为0.314 s，且其评估精度仅次于PSO-SVR和CSO-SVR模型，在高效评估谐波损耗的同时也具有较好的评估精度。而采用PSO、CSO算法优化SVR超参数，均增加了模型整体耗时。与PSO算法相比，CSO算法运算时间较长。CSO-SVR模型虽牺牲了一些运算效率，但可取得更高的损耗评估精度，可应用于评估精度要求高而即时性要求较低的场合，如离线评估等。

5 结论

针对谐波损耗解析计算精度不高的问题，文中提出采用CSO-SVR模型进行低压架空线路谐波损耗评估，利用电能质量综合试验平台实测获得的谐波损耗数据，对所提模型进行验证。结论如下：

(1) 运用SVR拟合能力强和泛化性能好的特点进行谐波损耗评估，评估结果优于物理解析、BP和RBF神经网络，无需复杂的公式计算或神经网络结构设计。

(2) 利用CSO全局搜索能力强、收敛精度高的优点，优化SVR训练参数。结果显示，超参数的优化有利于提升SVR模型性能，相比其他模型，CSO-SVR模型谐波损耗评估精度更高，评估性能更好。