BDS-3多频信号最优线性组合及特性分析

李毓照 杨维芳 闫浩文 王世杰 杨国林 苏小宁

1 兰州交通大学测绘与地理信息学院，兰州市安宁西路88号， 730070 2 地理国情监测技术应用国家地方联合工程研究中心，兰州市安宁西路88号，730070 3 甘肃省地理国情监测工程实验室，兰州市安宁西路88号，730070

全球卫星导航系统(global navigation satellite system,GNSS)是提供全球快速高精度位置服务的主要手段，已广泛应用于灾害监测、构筑物形变监测、车辆导航、自动驾驶等领域[1]。其中整周模糊度快速、可靠地固定是实现高精度快速导航定位的关键所在。已有研究表明，三频GNSS模糊度解算比双频模糊度解算更可靠[2]，TCAR(triple-frequency carrier ambiguity resolution)则是常用的三频载波相位模糊度解算方法，能有效提高大范围或困难环境下实时精密定位模糊度解算的效率和可靠性。

TCAR一般按照波长由长到短逐步解算超宽巷、宽巷及窄巷组合模糊度，最终实现所有模糊度的解算。而不同组合观测量具有不同的电离层延迟、噪声等特性[3]。根据构建组合观测量的波长、电离层延迟、噪声等3个标准，文献[4]提出用巷数(lane-number)表征组合观测量波长的特性，用电离层数(ion-number)来反映电离层延迟的影响；文献[5]系统地研究北斗区域卫星导航系统(BDS-2)三频载波信号线性组合观测量的特点；文献[6-7]用函数极值法求解BDS-2和GPS特定条件下的三频最优组合观测量系数；也有学者运用模糊数学中的聚类算法进行BDS-2和GPS三频最优组合观测值选取[8-9]。

目前，我国北斗全球卫星导航系统(BDS-3)可以播发B1C、B2a、B2b、B1I、B3I共5个频点的载波相位信号。理论上，四频和五频线性组合能得到更多波长更长、电离层延迟更小、噪声更低的组合观测量，进一步增强实时精密定位性能。已有研究采用BDS-3的五频观测数据构建多频相位模糊度解算(multi-frequency carrier ambiguity resolution, MCAR)模型，进行单历元模糊度解算初步研究，结果表明，随着频率数增加，模糊度固定成功率显著提高[10-11]，但高质量组合信号选取时，研究者分别考虑波长更长、电离层尺度因子更小、噪声比例系数更小3个条件主观判断确定高质量信号，不足以客观、准确地描述组合间的关系。为此，本文利用模糊聚类分析法构建模糊矩阵，分别实现BDS-3三频、四频及五频最优超宽巷组合观测量的获取，避免依据主观判断确定最优组合导致的“非此即彼”的硬分类；同时，分析不同频率条件下选取的最优组合在中短基线、中长基线、长基线3种场景下的特性。

1 GNSS多频信号线性组合

假设GNSS播发的多频信号按频率从大到小依次为f1、f2、…、fk，k表示GNSS频率数(k≥3)。根据GNSS线性组合观测理论，多频GNSS组合频率、波长、双差整周模糊度、观测噪声可依次表示为：

f(k)=i1f1+i2f2+…+ikfk

(1)

(2)

N(k)=i1N1+i2N2+…+ikNk

(3)

εφ(k)=i1εφ1+i2εφ2+…+ikεφk

(4)

式中，ik为组合观测量整数系数，c为真空中的光速。

相应的多频双差载波相位线性组合观测量可表示为：

(5)

式中，Φ(k)表示k个频率组合后的双差相位观测量，φk表示第k个频率的双差相位观测值。

根据GNSS频率值，对所有频率求最大公约数，将最大公约数定义为GNSS的基准频率f0，则f0满足：

f1=n1f0，f2=n2f0，…，fk=nkf0

(6)

式中，nk均为整数。

由此，组合观测值频率可表示为：

f(k)=i1f1+i2f2+…+ikfk=

(i1n1+i2n2+…+iknk)f0

(7)

令

L(k)=i1n1+i2n2+…+iknk

(8)

对于BDS-3系统，因其各载波频率均为定值，故而系数nk也为定值，所以L(k)是由整数组合系数ik决定的特定整数。

由波长与频率的关系可知：

λ(k)=λ0/L(k)

(9)

式中，λ0为基准频率对应的波长。

由此可知，组合观测值的波长仅与整数L(k)的大小有关。因此，将L(k)定义为表征组合观测量波长的参数，即巷数(lane-number)[3]。

基于组合观测量噪声方程(4)，假定各频率的载波相位观测噪声相等且独立，且满足εφ1=εφ2=…=εφk=εφ，则以周为单位的载波相位组合观测量噪声为：

(10)

式中，T(k)表示以周为单位的组合观测值噪声放大系数，且只与组合观测量系数有关。系数的平方和越大，组合噪声越大。

将多频双差相位线性组合观测量展开后，分别用β(k)、θ(k)表示一、二阶电离层延迟尺度因子，形式如下：

(11)

(12)

假定各频率相位观测值精度相同，即满足σφ1=σφ2=…=σφk≡σφ，则载波相位组合观测值精度为：

(13)

其中，定义μ(k)为噪声因子，形式如下：

(14)

根据GNSS组合观测量选取基本原则(波长较长、电离层延迟较小、噪声较小、保持模糊度整周特性)，针对BDS-3的三频、四频、五频信号，分别将同时满足ik∈[-10,10]、λ(k)≥2.93 m、|β(k)|≤4、T(k)≤15、μ(k)≤250的组合观测量作为高质量信号。据统计，BDS-3的三频、四频和五频高质量组合观测量数量及对比如图1所示。可以看出，高质量组合观测量数目随着频率数的增加急剧增长。

图1 BDS-3多频高质量组合观测量统计Fig.1 The statistics of BDS-3 multi-frequency and high-quality combinations

为保证MCAR模型的模糊度解算性能，本文采用模糊聚类分析法[1，9]，通过数据标准化、标定(建立模糊相似矩阵)和聚类，从众多高质量组合中进行BDS-3多频载波相位超宽巷最优组合观测量选取。

2 BDS-3多频线性组合

在实际应用中，不同基线场景下，模糊度解算的主要误差源不同。其中，短基线时，电离层延迟由于空间相关性强，可以通过双差进行削弱，则噪声成为影响基线解算精度的主要因素；而对于长基线，由于空间距离较大，电离层延迟和对流层延迟的影响是基线解算精度的主要影响因素。为更好地评价各组合的特性，引入总噪声水平(total noise level, TNL)的概念[3]:

(15)

式中，σTNL为相位观测量总噪声水平(单位周)，σorb为轨道误差，σtrop为对流层延迟误差，σI1和σI2分别为一阶和二阶电离层延迟误差，σε(k)为载波相位观测噪声。

假定3种场景：Ⅰ中短基线(d≤100 km)、Ⅱ中长基线(100200 km)，各项误差的精度如表1(单位cm)所示。

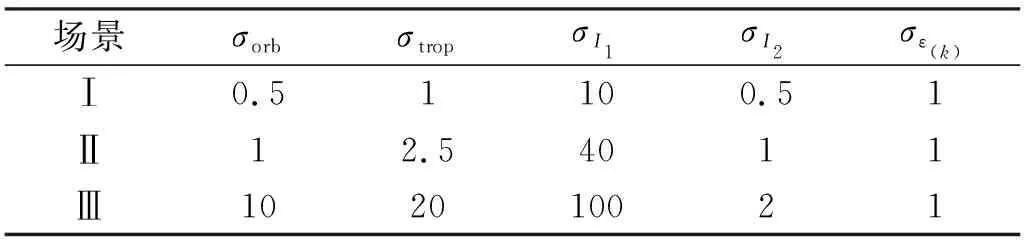
表1 不同场景下双差相位观测值的各项误差精度

BDS-3具有5类信号，根据文献[10]可知，BDS-3三频信号通常是指B1C、B3I和B2a，四频信号是指B1C、B3I、B2a和B1I，五频信号是指B1C、B3I、B2a、B1I和B2b。

由多频模糊度解算模型知，三频、四频及五频构建MCAR模型分别需要选择3个、4个及5个相互独立的线性组合，且其中必须包含1个窄巷组合观测量。因超宽巷组合更易于模糊度固定，故优先选择2个、3个、4个最优超宽巷组合与另外1个窄巷组合，共同构建不同频率下的MCAR模型。为此，表2、表3、表4分别给出模糊聚类分析法选取的BDS-3三频、四频及五频信号的最优超宽巷组合观测量及参数。

表2 BDS-3三频信号最优组合及相关参数

表3 BDS-3四频信号最优组合及相关参数

表4 BDS-3五频信号最优组合及相关参数

由表2可知，(1，-4，3)、(0，1，-1)两个组合是BDS-3三频信号中最优的组合观测量，且3种场景下，(1，-4，3)组合的σTNL均小于0.5周，理论上采用单历元取整即可固定其模糊度；而(0，1，-1)组合在长基线时，其σTNL为0.516 0周，略大于0.5周，故理论上难以实现单历元模糊度固定。

由表3可知，适用于四频MCAR算法的最优超宽巷组合可选择(1，-1，0，0)、(-3，3，1，-1)和(-2，2，1，-1)，在3种场景下的σTNL均小于0.5周，且最大的σTNL也仅为0.417 6周，均可实现单历元模糊度的取整固定。

由表4可知，五频MCAR算法的最优超宽巷组合可选择(-1，1，0，1，-1)、(0，0，1，-2，1)、(0，0，0，1，-1)、(1，-1，0，1，-1)，在3种场景下的σTNL均小于0.25周，能满足单历元模糊度取整固定的要求。

3 结 语

本文围绕BDS-3多频模糊度解算中最优组合观测量的选取问题，针对BDS-3三频、四频及五频信号，基于模糊聚类分析法分别实现了最优组合观测量的选取，并对各组合观测量在中短基线、中长基线及长基线3种场景下的特性参数进行分析，得出几点结论：

1)多频线性组合高质量信号随着频率数的增加急剧增多，BDS-3五频高质量组合数目是三频高质量组合数目的150多倍，是四频高质量组合数目的10多倍。

2)更多的频率有利于形成总噪声水平更小的线性组合，有利于实现单历元模糊度的快速固定及大范围精密定位。