基于多图卷积神经网络和注意力机制的学术新星预测方法*

单 辉,丁成鑫,赵中英,周明成，贾霄生,李 超,2

(1.山东科技大学计算机科学与工程学院,山东 青岛 266590;2.山东科技大学电子信息工程学院,山东 青岛 266590)

1 引言

学术新星是指那些正处于职业生涯初期，没有较多的出版物和引用，也没有在著名的会议或期刊上发表过文章，但未来能够快速崛起，成为该领域专家的研究人员。学术新星预测(Academic Rising Star Prediction)是学术评估领域中一个非常具有现实意义的问题，已经成为近年来的热门话题，并得到了广泛的探索[1 -3]。预测快速崛起的学术新星有助于解决资源配置、决策支持等实际问题。学术领域有一些评价指标，如g-指数、h-指数等[4 -7]能在一定程度上反映学者的研究成果。然而，这些指标往往需要较长时间的积累。而学术新星发表论文数量较少，引用次数较少，因此使用这些指标来识别学术新星是不合适的。现有的学术新星预测方法大多是基于PageRank算法进行改进的，Jin等人[5]最先将学术社会网络应用于发现学术新星任务，提出了基于作者合著网络寻找学术新星的算法—PubRank。Yan等人[8]将引用论文、引用期刊和引用作者等因素与PageRank算法相结合提出了P-Rank算法，用于计算论文、期刊和作者的排名。但是，预测学术新星本质上是发现未来具有较大潜力的学术新人，而不是根据作者当前所取得的学术成果对其进行排名。因此，这些方法的效果并不佳。

还有一些学者使用机器学习算法预测学术新星，常用的算法有决策树、支持向量机和神经网络等。文献[9]利用因子分析法找出反映学者活动特征的内在因素，利用神经网络分配权重，最后使用层次分析法预测学术新星。文献[10]提出了将机器学习算法用于学术新星预测，主要考虑了判别模型和生成模型。但是,这些算法忽略了作者间的社交关系，如合作关系、引用关系等，从而影响了预测的性能。

鉴于以上问题，本文提出了一种联合多图卷积神经网络和注意力机制的学术新星预测方法MGCNA(academic rising star prediction method based on Multi-Graph Convolutional Neural network and Attention mechanism)。该方法考虑了各种学术影响力评价指标，以此来生成作者最初的特征表示；然后采用图卷积神经网络学习不同类型网络中的作者特征，将作者的交互信息和属性信息结合起来，并引入注意力机制对不同类型网络的重要性进行分配，从而实现学术新星的预测。

本文的主要贡献如下所示:

(1)提出了一种联合多图卷积神经网络和注意力机制的学术新星预测方法MGCNA，能够将作者的交互信息和属性信息结合起来；

(2)考虑了影响作者引用次数增长的各种因素，构建了2种类型的网络，即合作网络和相似网络，能够挖掘作者间的多种关系；

(3)在大规模真实数据集上进行了大量实验，实验结果表明了方法的有效性。

2 相关工作

学术新星预测一直是学术评估领域最有意义的问题之一，它可以应用于各种实际任务。如一所高校想要招聘年轻教师，如何从一组候选人中识别出未来有潜力的学者，学术新星预测可以提供有用的参考；或者对于某一领域的初学者，学术新星预测能够帮助他识别出该领域最具潜力的学者，更快地熟悉该领域。

学术新星预测的方法主要分为2种，一种是基于社交网络的方法，另一种是基于机器学习的方法。基于社交网络的方法是将作者抽象为点，作者之间的合作关系抽象为边，利用图论的相关知识，计算节点的中心度等各种网络属性，根据作者在网络中的重要性对其排名，然后记录一段时间内作者排名的变化，分析排名的变化趋势，预测学术新星。其中合著者网络和引文网络使用最为广泛[11,12]。Sayyadi等人[13]提出了FutureRank算法，利用引文网络和论文发表时间计算论文未来的PageRank分数。Daud等人[14]考虑了引用作者、署名顺序和出版地等因素，提出了WMIRank(Weighted Mutual Influence Rank)算法，实验结果表明所考虑的特征在预测学术新星任务中非常有效。Zhang等人[15]提出的CocaRank(a Collaboration Caliber-based Method for Finding Academic Rising Stars)算法同样是综合论文、作者和期刊等因素预测学术新星，但是该算法在整合多种因素时处理得较为简单。由此可知，社交网络分析是实现作者学术影响力评估的有效方法。然而这些方法都只考虑了单一的网络(合作网络或被引网络)，只能建模作者间的一种关系(合作关系或引用关系)。

基于机器学习的方法其原理是将能够反映作者学术影响力的指标作为特征，然后构建拟合模型来预测冉冉升起的学术新星。文献[16]首先提出了一种基于引文质量和合著者影响力的层次加权评价模型，然后使用机器学习中的分类算法预测学术新星。Zhang等人[17]探索了一系列影响作者引用次数增长的因素，并将引用次数的增量作为回归任务的预测目标。Panagopoulos等人[18]提出了一种基于无监督学习的方法来预测学术新星。该方法为每个学者提取若干评估指标，根据一段时间内这些评估指标的变化，使用聚类方法对学者进行分类，从而识别出学术新星。然而基于机器学习的方法在特征选择上具有较强的主观性，同时没有考虑作者间的相互作用。

3 基于多图卷积神经网络和注意力机制的学术新星预测方法MGCNA

本节详细介绍本文提出的基于多图卷积神经网络和注意力机制的学术新星预测方法MGCNA。

3.1 问题定义

给定某领域一组新人作者集合U={u1,u2,…,uL}(指在某一年首次发表论文的作者)，其中L表示作者的数量，新人作者T年内发表的论文集合P={p1,p2,…,pm}，合作网络C(U,E1)和相似网络S(U,E2)，E1表示作者间的合作关系，E2表示作者间的相似关系。对于每个作者ui∈U，xi表示作者ui的特征向量，包含其T年内发表的论文数量、引用次数等属性。该方法的任务是识别出某研究领域未来的学术新星，即给定作者ui、特征向量xi、合作网络C(U,E1)和相似网络S(U,E2)，计算该作者Δt年后成为学术新星的概率p，可以形式化如式(1)所示：

f:(ui,xi,C,S,Δt)→p

(1)

3.2 属性特征提取

考虑能够影响作者ui未来引用次数增长的各种因素，生成作者最初的特征表示xi。表1列出了本文选择的Author、Social、Venue和Initial 4种类型的特征。下面给出每种类型的特征的详细描述。表1中所有特征的取值都是根据作者截止到目前的科研成果统计的。

(1)Author:作者未来引用次数的增长与其当前的学术水平息息相关。本文提取了5个与作者自身相关的特征：①发表论文数量；②总引用次数；③平均引用次数；④总贡献度；⑤平均贡献度。作者的贡献度是由作者的署名顺序反映的，排名越靠前的作者一般贡献程度比较高。本文采用S-index[19]计算一篇论文中作者的贡献度，如式(2)所示:

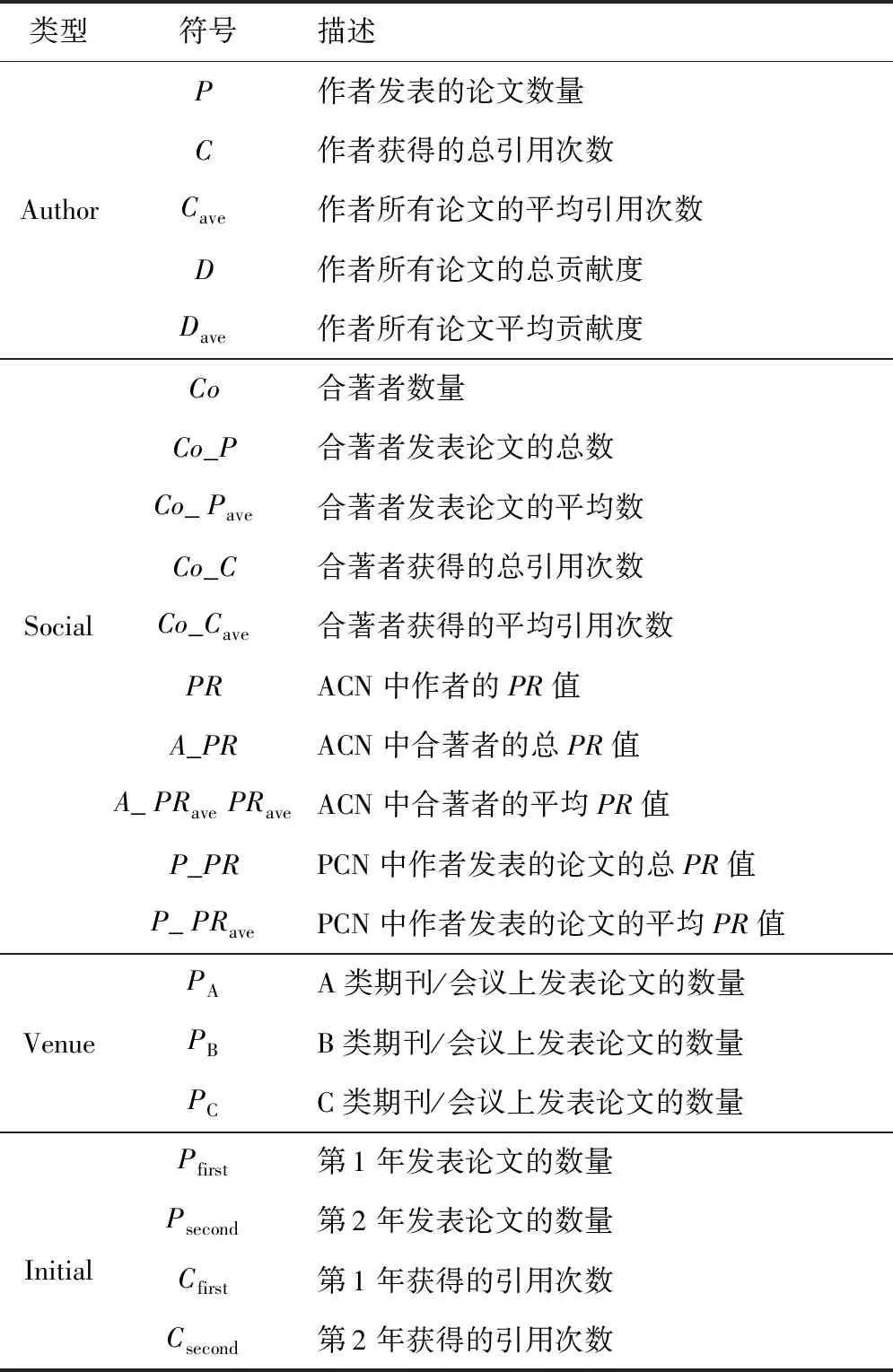
Table 1 Definition of features表1 特征定义

(2)

其中，k是作者的署名顺序，0≤S≤1。Q的计算如式(3)所示:

(3)

其中，N是该论文的作者总数,j表示合著者的排名序列。

(2)Social:作者间的社交活动也会对作者未来引用次数的增长产生影响。为了建模这种影响，本文构建了作者加权合著网络ACN(Author Collaboration Network)和论文被引网络PCN(Paper Citation Network)。在ACN中，边表示作者之间的合作关系，边的权值表示合作频率；在PCN中，边表示作者之间的“引用-被引用”关系，是一个有向网络。本文使用PageRank算法[20]量化节点的权重值。最终提取了10个社会属性特征:①合著者数量；②合著者发表论文的总数；③合著者发表论文的平均数；④合著者获得的总引用次数；⑤合著者获得的平均引用次数；⑥ACN中作者的PR值；⑦ACN中合著者的总PR值；⑧ACN中合著者的平均PR值；⑨PCN中作者发表的论文的总PR值；⑩PCN中作者发表的论文的平均PR值。

(3)Venue:出版物具有的影响力和声誉不同，从而对作者引用次数的增长会产生不同程度的影响。本文根据中国计算机学会(CCF)最新发布的推荐期刊/会议列表，统计作者在A、B、C 3个等级的期刊/会议上发表的论文数量。

(4)Initial:最后考虑了作者最初2年发表论文的数量和引用次数。最初的学术成果也能很好地表征作者未来引用次数的变化。本文考虑了作者第1年及第2年发表论文的数量和引用次数4个特征。

另外，由于不同特征的取值范围不同，需要对每个特征的取值进行归一化处理，从而得到作者最初的特征表示。

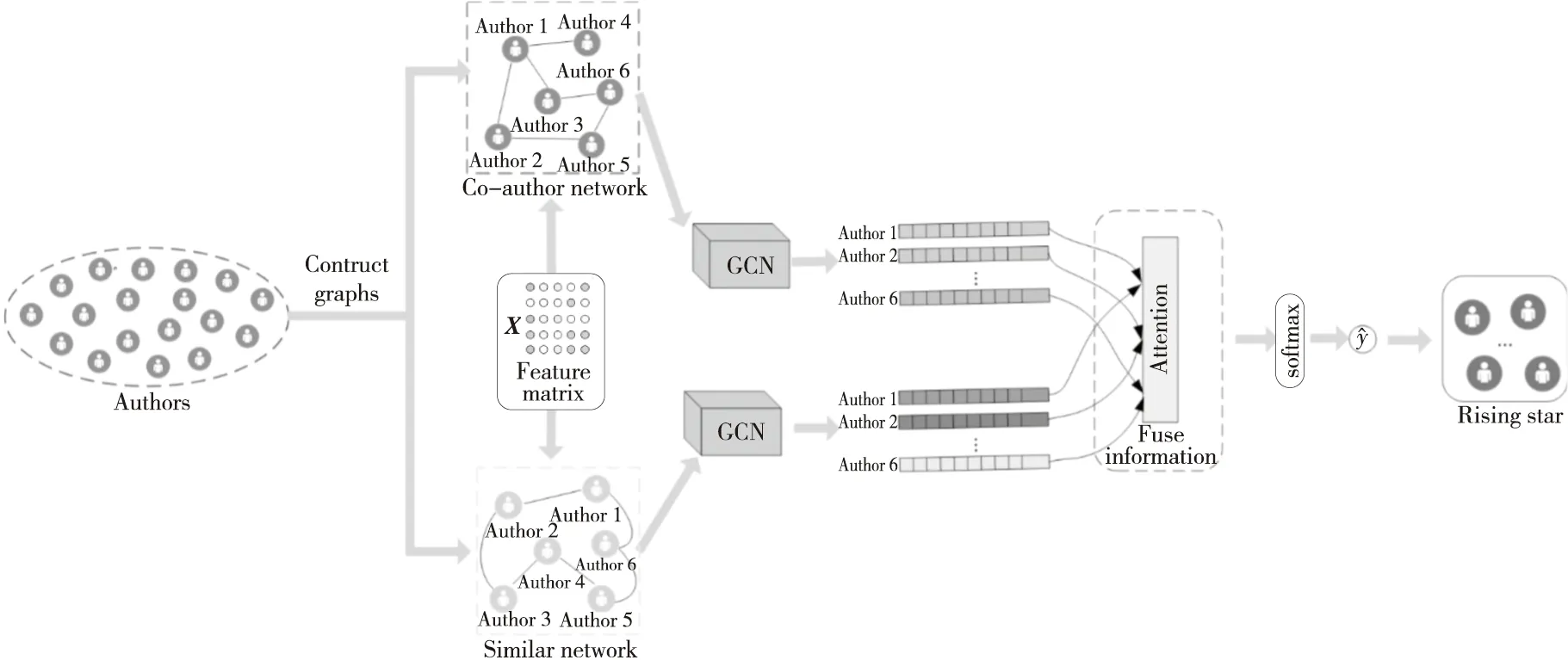
Figure 1 Overall framework of MGCNA 图1 MGCNA的整体框架

3.3 构建相似网络

对于每个作者ui∈U，找到与其特征向量相似度最高的n个邻居，设置边来连接他们，从而生成作者相似网络S(U,E2)。计算作者相似度的具体方法有很多，如余弦相似度、皮尔森相关系数和杰卡德相似度等。余弦相似度在比较向量之间的相似性方面简单高效，具有突出的优势，因此本文使用余弦相似度计算作者的相似度。令xi和xj表示作者ui和作者uj的特征向量，两者的余弦相似度sim(ui,uj)如式(4)所示:

(4)

3.4 预测方法

本文提出的学术新星预测方法MGCNA如图1所示。给定合作网络C(U,E1)、相似网络S(U,E2)和特征矩阵X={x1,x2,…,xL}(X∈RL×d)，d是特征向量的维数，xi(i∈[1,L])表示作者的特征向量，使用图卷积神经网络进行图编码。图卷积网络(Graph Convolutional Network)是卷积神经网络的一种变体，基本思想是聚合邻居节点的特征，将其作为目标节点的特征表示[21]。对于合作网络C(U,E1)，图卷积神经网络将原始图结构C(U,E1)映射到一个新的特征空间fC→fγ，每一层的传播规则如式(5)所示:

(5)

(6)

(7)

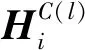
由于不同类型网络所代表的信息的重要程度不同，本文引用注意力机制为不同网络学习到的表示分配不同的权重，注意力系数如式(8)和式(9)所示:

(8)

(9)

(10)

(11)

(12)

4 实验与结果分析

为了评估本文方法的性能，在真实数据集上进行了大量的实验，实验结果表明了本文提出的MGCNA在学术新星预测任务上的有效性。

4.1 数据集介绍

本文选用的数据是来自著名在线索引数据库ArnetMiner[22]中的Academic Social Network数据集(http:∥www．aminer．cn/aminernetwork)。该数据集是一个被广泛使用的开放数据集，包含1936～2014年间发表的两百多万篇论文，且每篇论文都包含题目、作者、摘要、出版时间、出版地和参考文献等信息。除此之外，还包含作者信息和合著关系信息。本文从该数据集中提取1996～2005年的论文数据，共617 829篇。再根据作者的研究兴趣信息将作者划分为5个研究领域，分别预测不同领域的学术新星。

4.2 评价指标

为了衡量MGCNA的有效性，本文使用精确率(precision)、召回率(recall)和F1 3个指标来评价MGCNA和其他对比方法的效果。具体地，精确率、召回率和F1的定义分别如式(3)～式(5)所示:

(13)

(14)

(15)

其中，TP表示实际是学术新星被预测为学术新星的作者数量；FP表示实际不是学术新星被预测为学术新星的作者数量；FN表示实际是学术新星被预测为不是学术新星的作者数量。

4.3 基线方法

为了验证MGCNA的性能，本文将MGCNA与以下几种方法进行对比。

(1)RF(Random Forest):通过构建多个决策树对数据进行分类的方法。

(2)SVM(Support Vector Machine):一种二分类模型，通过求解几何间隔最大的分离超平面对数据进行分类。

(3)PubRank[5]:一种基于作者合作网络和论文质量预测学术新星的方法。

(4)MLP(Multi-Layer Perceptron):一种由输入层、隐藏层和输出层构成的简单神经网络。

(5)C-GCN(Graph Convolutional Network based on author Collaboration network):只考虑作者合作网络,使用图卷积神经网络预测学术新星的方法。

4.4 实验结果

本文将实验数据集划分为1996～2000年和2001～2005这2个时间段，对2个时间段内的学术新星进行预测。实验参数的具体设置如下:t=1996,2001，即2个时间段的学术新人集合分别为在1996年和在2001年第1次发表论文的所有作者,Δt=5,T=5，文献[23]指出有研究表明学术生涯的前5年是一个至关重要的时期，对学者整个研究生涯起着关键作用。MGCNA中，网络的层数l=2,嵌入的维度c=32,学习率lr=0.01,采用dropout防止过拟合，dropout=0.5,n=10。表2显示了不同领域的新人作者的数量。

本文选用ARIC(Average Relative Increase in Citations)[10]衡量新人作者引用次数的变化，根据ARIC值的大小对新人作者进行排名，将排名前10%的作者视为学术新星，令其标签值为1。与引用次数增长量不同的是，ARIC能反映引用次数随时间的增长变化，其定义如式(16)所示:

(16)

ΔCi=(Ci-Ci-1)/Ci

(17)

其中，Ci表示在第i年作者论文的被引用次数；ΔCi表示在第i年作者论文被引用次数的增长率。

每次训练重复10次，取其平均值作为最终结果，2个时间段的实验结果分别如表3和表4所示，其中黑体表示最优值。

MGCNA在1996～2000年数据集上的precision、recall和F1值比RF和SVM分别最少提升了2.49%,2.67%,2.58%和8.4%,8.3%,8.17%；在2001～2005年数据集上的precision、recall和F1值比RF和SVM分别最少提升了3.69%,3.78%,3.99%和8.7%,8.4%,8.6%，表明MGCNA的性能优于机器学习的分类方法。相比于PubRank，MGCNA在2个时间段的数据集上的precision、recall和F1值分别最少提升了14.07%,14.07%,14.07%和14.42%,14.42%,14.42%，表明考虑作者自身的特征表示能够有效地提高方法的性能。与MLP相比，MGCNA在2个时间段的数据集上的precision、recall和F1值分别最少提升了2.81%,2.53%,2.84%和2.66%,2.41%,2.78%。最后与只考虑作者合作网络的C-GCN相比，MGCNA在2个时间段的数据集上的precision、recall和F1值分别最少提升了1.13%,1.12%,1.13%和1.67%,1.44%,1.52%，这表明融入作者间的相似关系是有效的。

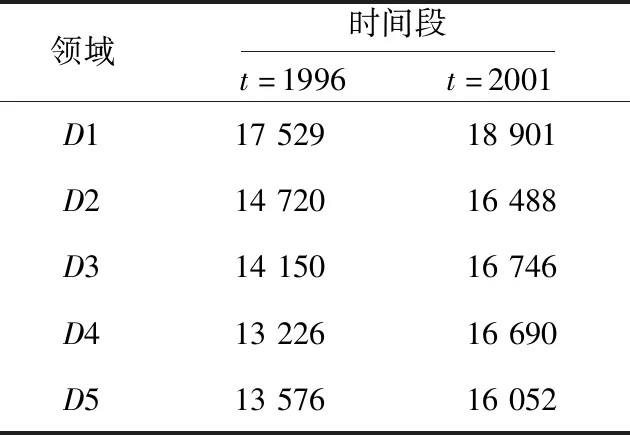
Table 2 Number of young authors in different domains表2 不同领域新人作者的数量

Table 3 Comparison of experimental results on data from 1996 to 2000 表3 1996～2000年数据集上实验结果对比

Table 4 Comparison of experimental results on data from 2001 to 2005表4 2001～2005年数据集上实验结果对比

4.5 参数敏感性分析

本节以D1领域的数据为例，分析MGCNA中各参数对实验结果的影响。图2显示的是图卷积层数l对实验结果的影响。从图2中可以看到，随着图卷积层数的增加，MGCNA的F1值先增大，当l=2时，F1值是最大的，此时再增加图卷积的层数，F1值反而逐渐减小。这是因为图卷积层数较大时，会将距离较远的邻居聚合在内，从而影响MGCNA的性能。

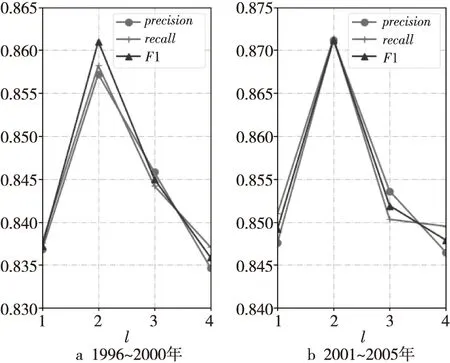
Figure 2 Effect of layer number of graph convolutional neural network on MGCNA 图2 图卷积神经网络层数对MGCNA的影响

图3显示的是嵌入维度c对MGCNA性能的影响。可以看到，当c=32时，MGCNA的性能最好，原因是嵌入维度较小时，会出现欠拟合，而嵌入维度较大时则会出现过拟合。相似邻居的数量n与MGCNA性能的关系如图4所示，n的最优取值为10。当n过大时，会将相似度较小的邻居考虑在内，从而增加噪声数据，使得MGCNA性能下降。

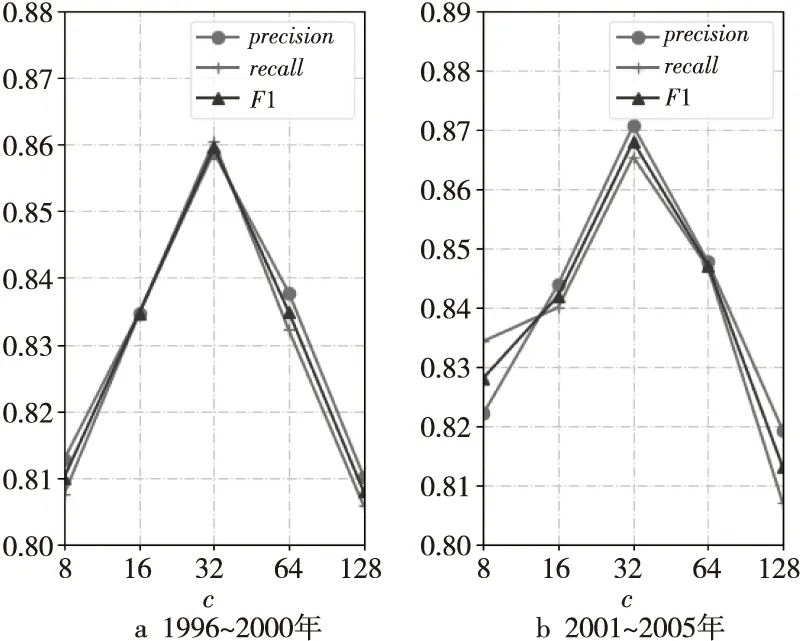
Figure 3 Effect of embedding dimension on MGCNA 图3 嵌入维度对MGCNA的影响

Figure 4 Effect of the count of similar neighbors on MGCNA图4 相似邻居数量对MGCNA的影响

5 结束语

本文将学术新星预测问题定义为预测在给定的学术新人集合中未来引用次数增长较快的学者。为了解决这个问题，本文首先探索了一系列能够影响作者论文引用次数增长的各种因素，以此生成作者最初的特征表示。然后从多角度建模作者间的关系，如合作关系和相似关系，使用图卷积神经网络学习作者节点的表示。最后使用注意力机制将学习到的表示进行融合，预测未来的学术新星。本文使用ArnetMiner平台中的大规模学术社交数据集来评估方法的性能，实验结果表明，本文提出MGCNA在效果上优于现有的方法。在下一步的工作中，考虑将时间因素融入到方法中，进一步改进方法的预测性能。