基于EMD距离的稀疏自编码器*

范 韫

(国防大学政治学院,上海 200433)

1 引言

近年来，深度学习在计算机视觉、自然语言处理和语音识别等领域取得了突破性的进展。深度学习强大的表征学习能力使其可以有效地使用低维度的稠密向量或高维度的稀疏向量来表征图像或者自然语句的语义。自编码器(Autoencoder)使用编码器-解码器的架构在目标真实样本与重构样本最小化失真的基础上，通过编码器得到真实样本的编码用于下游任务，通过解码器得到真实样本的重构样本用于优化自编码器。自编码器优秀的表征学习能力使其在图像检索[1]、数据降维[2]中得到广泛应用。

随着深度学习的快速发展，自编码器衍生出诸多变种，如对损失函数增加L1/L2范数惩罚项的正则化自编码器、对输入增加噪声增强模型鲁棒性的去噪自编码器[3]和基于贝叶斯变分推断的变分自编码器[4]等。其中，通过引入稀疏性概念，将输入映射到高维空间，抑制神经元激活的稀疏自编码器SAE(Sparse AutoEncoder)在分类问题上取得了较优的效果[5]。稀疏自编码器也广泛地应用于目标检测[6,7]、行人分类[8]、异常检测[9,10]和视频摘要生成[11]等现实场景。

在自编码器的基础上，SAE通过抑制神经元激活来产生比样本维度更高的稀疏编码，从而捕捉样本的内在特征结构[12]。当激活函数为Sigmoid函数时，SAE可以通过在损失函数上增加神经元输出分布与伯努利分布的测度的惩罚项来加强模型稀疏性，使得神经元尽可能接近激活函数Sigmoid的最大下确界0，从而达到通过抑制神经元激活来获得稀疏编码的目的。衡量分布距离的测度通常选择KL(Kullback-Leibler)散度。KL散度在机器学习中有着广泛的应用，例如在典型的多分类任务中，当数据样本采用独热编码，模型采用Softmax函数计算分类概率分布，损失函数是计算真实值与预测值的交叉熵时，优化交叉熵退化为优化样本分类的独热编码与模型输出的分类概率分布之间的KL散度。

由Goodfellow等[13]提出的生成式对抗网络GAN(Generative Adversarial Network)是近年来的研究热点。GAN通过神经网络学习数据集的复杂分布，可以生成逼真的图像。GAN通过判别器来区分真实图像和生成图像，并指导生成器不断优化产生能够以假乱真的图像。判别器通过KL散度度量数据的真实分布和生成器的生成数据分布的距离来进行图像真假的判别。使用KL散度的GAN存在梯度消失和模式塌陷的问题，训练过程不够稳定。为了解决这一问题，Martin等[14]分析了KL散度在GAN中的应用问题并提出了基于Wasserstein距离的WGAN(Wasserstein GAN)，通过截取模型参数满足Wasserstein距离的Lipschitz约束，有效地提升了模型的训练稳定性。同时在WGAN中也证明了Wasserstein距离相比于KL散度和JS(Jensen-Shannon)散度，更加适用于优化神经网络。Wasserstein距离也被直接用于自编码器中，取得了较好的效果[15]。

受Wasserstein距离在GAN中的成功应用的启发，本文将EMD(Earth Mover Distance),即Wasserstein-1距离应用于SAE的损失函数的正则化，并同使用KL散度和JS散度正则化的SAE进行对比。实验结果表明，使用EMD距离作为惩罚项的SAE可以进一步收敛至局部最优解，并且编码可以更加稀疏。

2 基本理论

2.1 稀疏自编码器架构

SAE采用编码器-解码器的架构。如图1所示，编码器E将数据样本xi编码为ei，解码器D将编码ei解码为yi。SAE的目标是让xi与yi尽可能相似，其最小化目标函数如式(1)～式(3)所示：

(1)

(2)

(3)

Figure 1 Framework of sparse autoencoder图1 稀疏自编码器的架构

2.2 KL散度与JS散度存在的问题

JS散度的定义如式(4)所示：

(4)

(5)

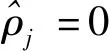
Figure 2 Problems of KL divergence and JS divergence图2 KL散度与JS散度的问题

2.3 EMD距离

EMD距离即Wasserstein-1距离，其定义如式(6)所示：

(6)

其中，Π(ρx,ρy)表示随机变量x和y的所有联合概率γ(x,y)分布的集合，γ(x,y)的边际分布分别为ρx与ρy。EMD距离最初在图像检索的相似度计算中被引入[16]，用于计算将分布ρx移动到分布ρy所需要的最小工作量，与运筹优化领域的经典运输问题类似，只是在约束项上加入了分布条件的约束。当分布ρx的支撑集supp(ρx)与分布ρy的支撑集supp(ρy)不相交或者相交很少时，EMD距离仍会随着supp(ρx)与supp(ρy)的距离变换而变换，所以相比于KL散度和JS散度有更好的鲁棒性。

此外，在WGAN中，Wasserstein距离被证明生成器的参数如果连续，那么Wasserstein距离作为损失函数也是连续的，而JS散度和KL散度都不具有此性质，所以EMD距离更适用于优化神经网络。

3 基于EMD距离的稀疏自编码器SAE-EMD

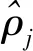
(7)

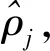
Figure 3 Plot of KL divergence,JS divergence and earth mover distance when ρ=0.2图3 当ρ=0.2时，KL散度、JS散度与EMD距离的取值对比

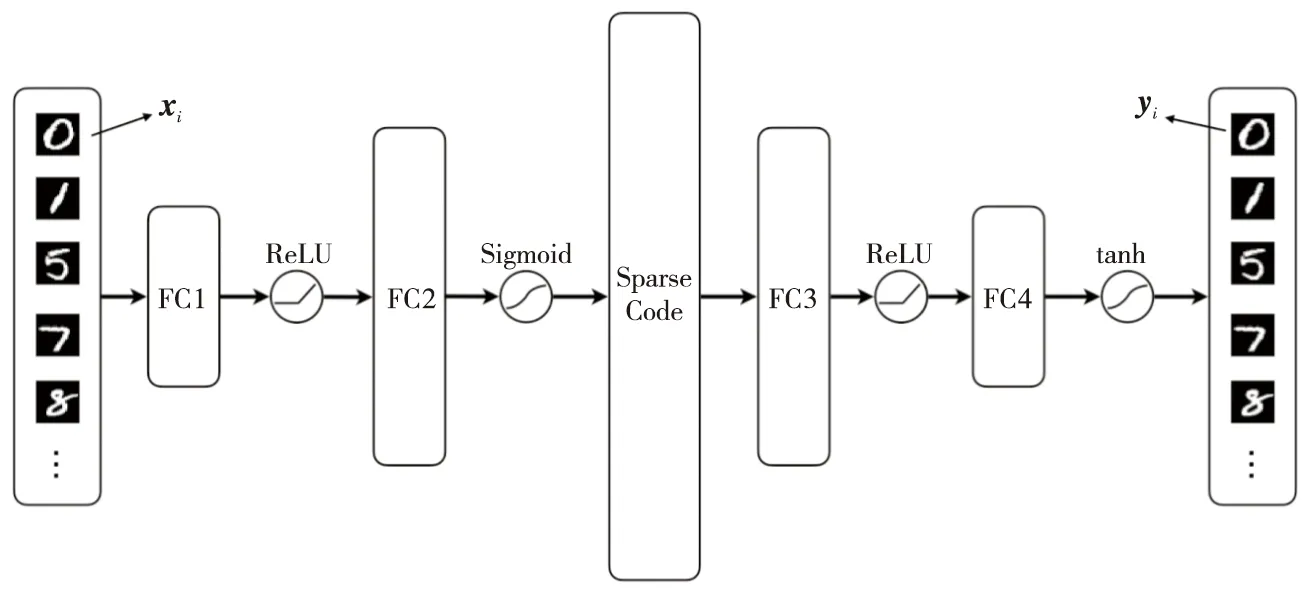
Figure 4 Structure of sparse autoencoder for experiment 图4 用于实验的稀疏自编码器结构

4 实验

4.1 实验设计

为了验证SAE-EMD的编码效果，设计实验所采用的SAE网络结构如图4所示，网络采用浅层结构，避免网络结构过深带来的过拟合和梯度消失问题造成实验结果无法区分不同正则化方法的差异。SAE的编码器由全连接层FC(Fully Connected)1-ReLU(Rectified Linear Unit)-全连接层FC2-Sigmoid组成，解码器由全连接层FC3-ReLU-全连接层FC4-tanh组成。

实验数据集为MNIST手写数字识别数据集[17]和QMNIST手写数字识别数据集[18]，数据为0～9的手写数字图像(大小28×28)，其中MNIST训练集包含60 000幅图像，测试集包含10 000幅图像。QMNIST针对MNIST的测试数据集的丢失部分进行了重构，采用尽量和MNIST图像预处理过程相似的方法，重新生成了60 000幅测试图像，以测试图像的增加是否增强了实验结果的可信度。实验所采用的网络全连接层FC1～FC4的参数维度分别为784×1568,1568×3136,3136×1568,1568×784。网络的损失函数如式(8)所示：

(8)

4.2 实验结果及分析

为比较不同SAE的编码效果，计算在不同λ和ρ的情况下，测试集图像编码的均值，定义如式(9)所示：

(9)

(10)

Table 1 Comparison of code means generated by different SAEs on MNIST test set and QMNIST test set表1 不同SAE生成的MNIST测试集和QMNIST测试集编码均值的对比

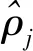
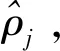
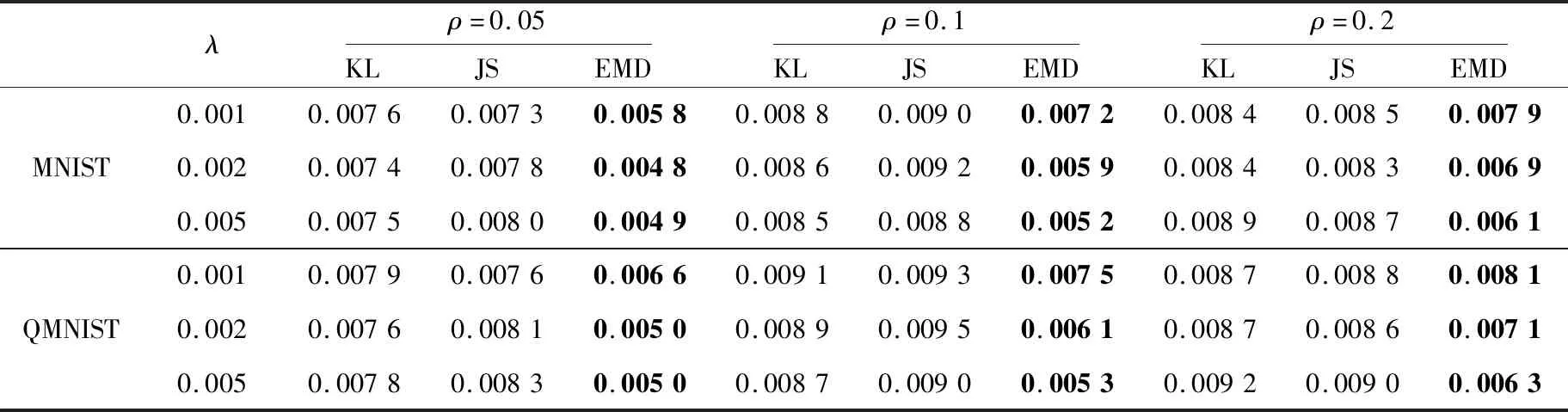
Table 2 Comparison of average MSE of different SAEs on MNIST test set and QMNIST test set表2 不同SAE在MNIST测试集和QMNIST测试集上的平均MSE对比

Figure 5 Spatial code means generated by different SAEs on MNIST test set 图5 不同SAE生成的MNIST测试集编码在空域上的均值分布

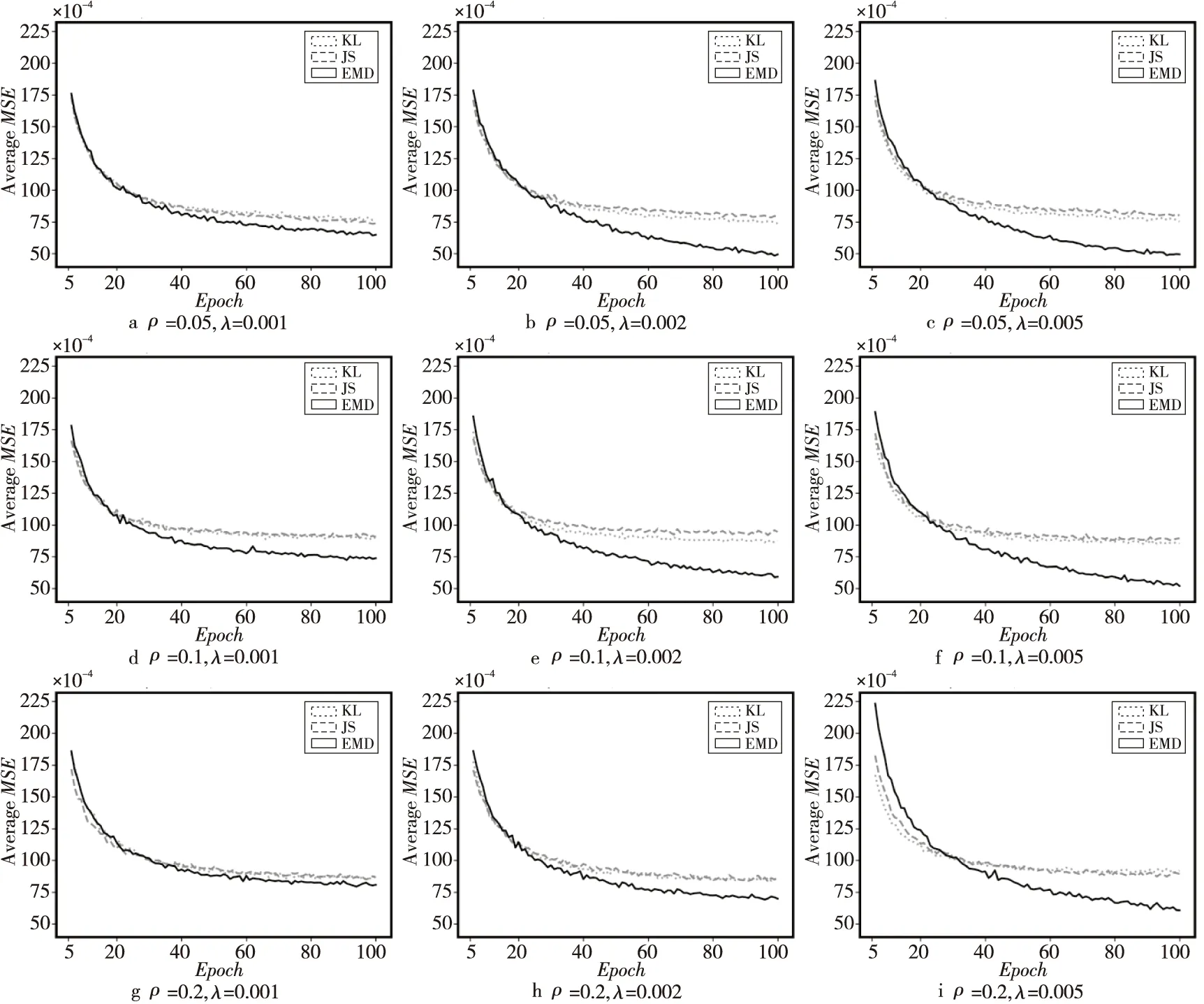
Figure 6 Average MSE of each epoch on MNIST test set 图6 MNIST测试集上每一轮次的平均MSE

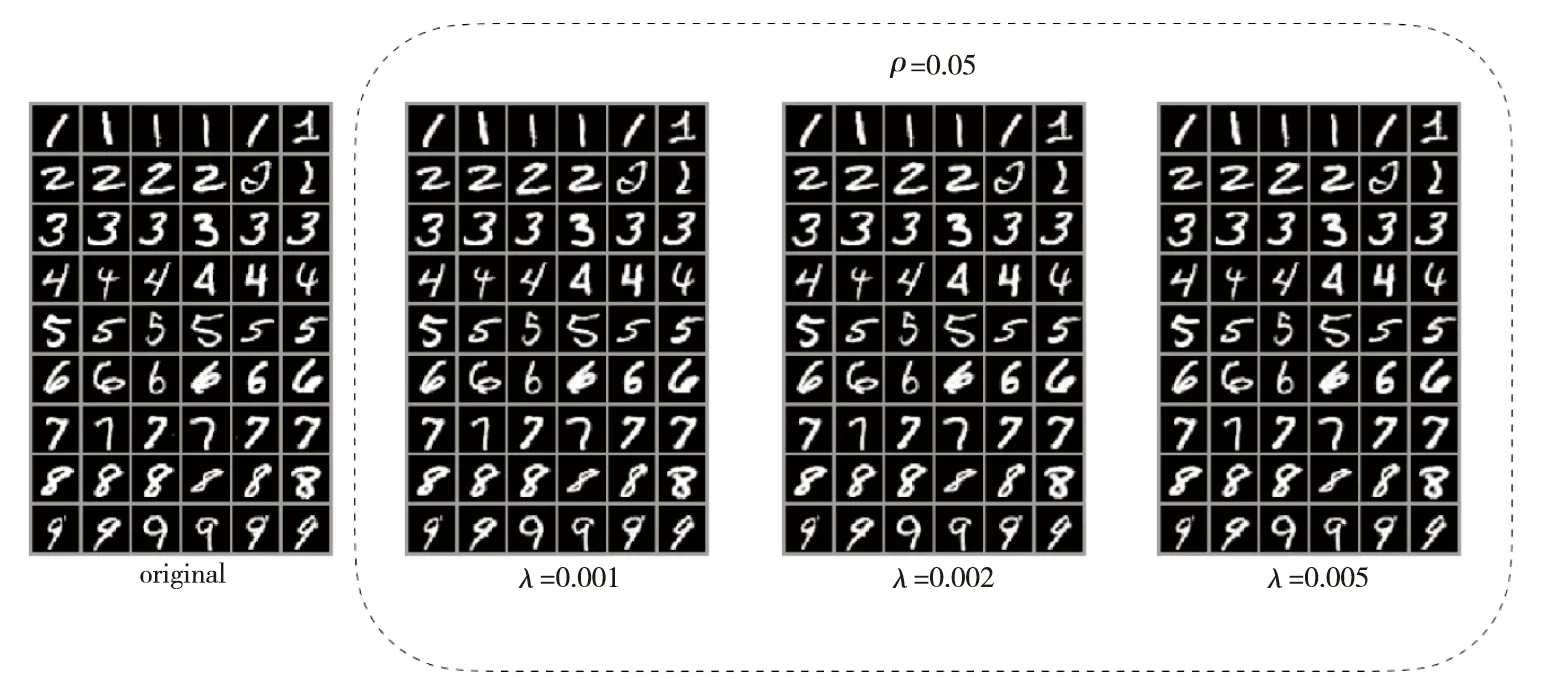
Figure 7 Comparison of original random samples from MNIST test set and correspoding reconstructed samples generated by SAE-EMD when ρ=0.05图7 当ρ=0.05时，MNIST测试集随机样本与SAE-EMD产生的重建样本对比

为比较不同SAE的收敛效果，本文直接使用每个轮次(Epoch)训练的SAE，将MNIST测试集作为验证集，计算平均MSE。将前5个轮次作为预热阶段，实验结果如图6所示。SAE-EMD在前25个左右的轮次收敛速度接近于SAE-JS和SAE-KL的。在之后的阶段，SAE-JS和SAE-KL的平均MSE基本不再下降，而SAE-EMD仍呈较为明显的下降趋势，特别是当λ较大时，SAE-EMD的下降趋势明显高于SAE-JS和SAE-KL的，SAE-EMD可以进一步地向局部最优解收敛。

如图7所示是当ρ=0.05时，λ取不同值时MNIST测试集随机样本与SAE-EMD产生的重建样本的对比，从图7中可见重建图像与原始图像基本无异。SAE-EMD很好地还原了手写数字图像。在QMNIST测试集上也得到了与上述相同的实验结果，本文不再赘述。

5 结束语

深度学习强大的表征学习能力极大地推动了人工智能在各个领域的发展。表征学习一直是机器学习领域的研究热点，深度学习很大程度上解决了如何使用模型自主学习数据的内在特征替代复杂低效的手工特征的问题。作为表征学习的重要组成部分，稀疏自编码器的稀疏表征有效地学习了样本的内在结构特征，为下游任务提供了便利。本文提出了基于EMD距离的稀疏自编码器。实验比较与分析显示，相比于带KL散度与JS散度惩罚项的稀疏自编码器，基于EMD距离的稀疏自编码器可以减少真实样本与重构样本的损失，并且当稀疏惩罚增大时，可以进一步压缩编码，从而节省了编码的存储空间，降低了下游任务使用编码的空间和时间计算复杂度。