金属基复合材料原位反应相场模型*

郭灿 康晨瑞 高莹 张一弛 邓英远 马超 徐春杰 梁淑华‡

1)(西安理工大学材料科学与工程学院,西安 710048)

2)(中信戴卡股份有限公司材料研究中心,秦皇岛 066000)

原位反应法制备金属基复合材料具有增强体与基体间无杂质、无污染、颗粒分布均匀等优点,已成为制备金属基复合材料的一种重要方法,揭示其动力学机制及规律具有重要的理论及工业价值.然而,原位反应过程具有反应时间短、随机发生、温度高等特点,目前采用原位实验观测其反应过程仍存在较大困难.本文采用相场法模拟金属熔体内的原位反应过程,首先建立了能够描述双束金属熔体界面反应形核的相场模型,并采用该模型模拟了不同参数下相界反应形核过程.结果表明,形核率随着曲率半径及噪声强度的增大而增大,小曲率半径及强噪声条件下新相颗粒尺寸分布更加均匀,形核率随着过冷度的增大而先增大后减小.

1 引言

金属熔体原位反应生成增强相是制备金属基复合材料的一种重要方法.因具有增强相与基体间界面清洁、可控、结合强度高,以及制备方法简单等优势,该方法一经提出,其反应热力学及动力学过程就得到了广泛的研究[1−8].郭明星等[1]利用基本热力学原理分析了Cu-B 和Cu-Ti 双束母合金熔体碰撞时TiB2形成过程,提出原位反应以相界处异质形核为主;杨滨等[2]则研究了铝熔体内原位反应生成TiB2的热力学机制;张来启等[3]计算分析了MoSi2-SiC 体系的反应热力学过程.在反应动力学上,孙靖[4]讨论了合金元素对TiB2颗粒形貌及生长动力学过程的影响;Qu 等[5]采用同步辐射技术研究了Cu6Sn5相的反应动力学过程.而Li等[6]采用实验方法研究了原位反应温度对增强相ZrB2颗粒大小的影响,并讨论了不同工艺条件下增强相颗粒的生长和团聚情况.近年来,随着复合材料的发展,多增强相竞争反应动力学问题也逐渐得到人们的关注.Jiang 等[7]研究了Cu 基复合材料原位反应中TiB 与TiB2竞争反应的析出过程.Lan 等[8]则讨论了原位反应制备的铜基复合材料中混杂增强体的竞争形核机制.

当前不同复合材料体系的原位反应热力学原理以及化学反应路径已经得到充分揭示.然而,因其反应动力学过程涉及到原子长程扩散、界面反应、液固相变、竞争形核以及晶粒长大等过程,是一个多尺度、多物理场耦合的复杂问题,其反应动力学过程及机制仍需进一步研究.由于金属熔体不透明,同时原位反应过程具有温度高、速度快、随机发生的特点,通过原位实验观测其反应动力学过程仍存在较大困难.所幸,随着计算机技术及计算材料科学的兴起,数值模拟已成为材料加工过程中微观组织演化机制研究的重要手段.

凝固过程研究常用的模拟方法有蒙特卡罗(Monte Carlo,MC) 方法[9]、元胞自动机(cellular automata,CA)法[10]、相场法(phase field method,PFM)[11].其中,MC 方法是一种以概率统计理论为基础的模拟方法,该方法在形核率计算以及形核路径问题上得到了广泛应用,然而MC 方法不能很好地处理固-液界面,进而限制了其在原位反应动力学问题上的应用.CA 法是一种网格动力学模型,已成功应用于枝晶生长、共晶凝固、形核等[12−14]问题研究中,然而CA 法无法直接获取计算过程中的界面信息,同时易受网格性质的影响,很难从物理本质上反映界面反应过程.PFM[15]是以Ginzburg-Landau 理论为基础建立起的一种能够准确描述系统随时间演化的数学模型,该方法避免了上述两种方法中的复杂界面追踪问题,且易于耦合其他物理场(如噪声场、速度场、成分场等),现已在形核、颗粒团聚、粗化、枝晶生长等[16−20]问题上得到了广泛应用,这为研究复合材料原位反应动力学过程提供了新方法.Pan 等[21]采用PFM模拟了铁素体与液态金属在1768 K 附近反应生成γ相的包晶反应过程,并重点讨论了过冷度对界面反应动力学的影响.柯常波等[22]采用PFM 研究了Cu6Sn5相在铜锡界面上的生长动力学行为.2018 年,Shi 等[23]还建立了能够描述晶界处异质形核的相场模型,并研究了界面性质对异质晶核形貌及形核点位选择的影响.这些研究使我们对相界反应有了进一步的认识,然而,这些工作大多采用预制晶核或人为预设形核条件的方式来产生新相晶核,不能反映真实相界反应过程新相生成随机性这一特点.同时,这些模型很难扩展应用到多相竞争反应形核过程的研究.

本文采用相场法模拟金属熔体内的原位反应过程,首先建立能够描述双束金属熔体界面反应形核的相场模型,而后使用新建立的相场模型模拟不同过冷度、界面曲率、噪声强度等条件下增强相的原位反应过程,分析反应条件对增强相颗粒形核率以及尺寸分布的影响.本文所建原位反应模型不仅能够实现噪声诱发随机形核过程,更重要的是可以方便地通过插值函数构造来实现多相竞争形核的复杂问题研究.

2 原位反应相场模型

系统总自由能泛函为

式中c为浓度场;ηi是第i个颗粒的序参量场;kc和kη为梯度项系数,本文取kc=10,kη=0.5;f(c,η1,η2,···,ηn)为体自由能密度函数,

其中,ΔHm为结晶潜热,ΔT为过冷度,Tm为理论结晶温度,文中过冷度参数为0.2Tm,w和ε为常数,本文取w=1,ε=2000.原位反应涉及到两相界面处的相变形核,先在小过冷时通过方程(2)得到两个成分不同的液相,而后通过构造一个浓度-颗粒序参量关联函数实现低温条件下的相界形核.本文采用一个单相插值函数ς(c) 作为窗函数来实现某特定成分固相的形核,

式中,c0为新相平衡成分,本文取c0=0.5,新相成分范围随着高斯峰峰宽增大而增大,本文取α=1/6为常数.

动力学方程为

式中M和L为动力学系数,本文取M=100,L=1.ξc和ξη分别表示浓度场和序参量场的噪声项.本文采用多物理场有限元求解器(multiphysics objectoriented simulation environment,MOOSE)求解动力学方程,时间步长为0.1,空间步长Δx=Δy=1,计算区域为256Δx×256Δy的正方形区域.初始条件为,计算区域中心部分为成分c=1 的液相,外围区域为c=0 的液相,周期性边界条件.相界处反应形核过程为随机噪声诱发的相变过程,为减小误差每组参数并列计算5 次,本文所得形核率以及尺寸分布均为5 组模拟结果的统计平均值.

3 结果与讨论

图1(a)—(c)为两相界面为平直界面时的原位反应形核过程的相场模拟结果,图中蓝色区域为c=0 的液相,红色区域为c=1 的液相,固相晶核为黄色区域,其成分为c=0.5.可以看出,新相形核在液相熔体界面处产生,其反应过程与Guo等[24]的原位反应物理模型一致,由于本算例未考虑界面各向异性,图中新相晶核沿相界对称生长.随着演化进行,已有晶核不断长大并有新晶核不断形成.图1(d)为图1(a)中黑色实线上的成分随时间的演化曲线,可以看出,t=43.8 时刻,黑直线横穿界面处尚未发生形核;当t=45.7 时,熔体界面处出现c=0.5 的平台,即新相形核,而后平台不断扩展,对应图1(a)—(c)中的新相晶核长大过程.这充分证实了新模型能够有效模拟相界处原位反应形核过程.

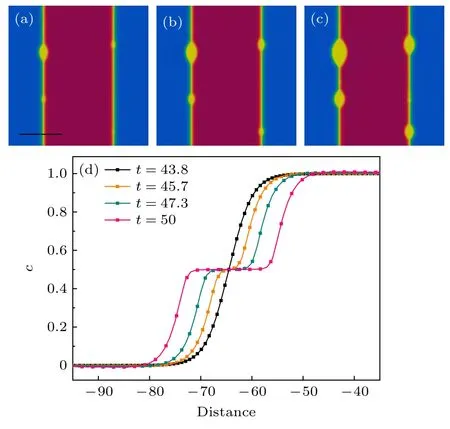
图1 (a)—(c)原位反应形核过程,红色区域为c=1 的液相,蓝色区域为c=0 的液相,黄色区域为c=0.5 的固相;(d) 沿图(a)中黑直线上的成分场随时间的演化曲线Fig.1.(a)–(c) Snapshots of the in-situ reactive process,the blue and red regions represent melt phases with c=0 and c=1,respectively.The yellow region is the new solid phase.(d) Temporal evolution of the concentration filed across the solid black line in panel (a).

3.1 界面曲率对原位反应形核过程的影响

实际双熔束流体混合后的两相界面中的平直界面比例很小,大多呈复杂界面形貌,不同混合状态会导致不同位置处的曲率存在较大差距,进而导致不同部位的形核及颗粒尺寸分布状况存在差异.图2 为不同曲率半径条件下熔体相界处的原位反应形核过程,从左到右,左侧3 张图为bnds 场演化图(bnds 用于区分系统内的相,其具体数值为),右侧3 张图为对应时刻的浓度场演化图.其中模拟参数设置为kc=10,噪声强度δ=0.01,过冷度参数为0.5.由图2 可知,随着演化进行,成分为c=0.5 的新相不断在两相界面处择优形核,其形核点位置及平衡成分不因曲率变化而偏离相界.随着形核过程的不断发生,两相界面位置不断被新相占据,当异质界面耗尽时形核过程终止,这与经典异质形核理论动力学过程相符合.进一步可以发现,晶核数目随着曲率半径减小而减小,这是由于曲率半径减小会导致两相反应界面面积减少,进而导致其晶核数目降低.

为了定量表征曲率半径对原位形核过程的影响,图3 统计了不同曲率半径的单位体积内的晶核个数随时间的变化曲线,其斜率为形核率.可以看出,中间阶段的晶核数目-时间近似呈线性关系,即此时原位反应过程的形核率为常数(稳态形核率),这表示新晶核形核与晶粒长大过程连续发生,这与经典形核过程的模拟结果一致[25].图4 为稳态形核率-曲率半径曲线,可以看出,形核率随着曲率半径的增大而增大,即较大的界面曲率半径更有利于形核,这与王巍和付立铭[26]研究的铁素体形核的结果是一致的.

图3 不同曲率半径下的晶核数目随时间演化图 (a) ρ=30;(b) ρ=50;(c) ρ=60;(d) ρ=80Fig.3.Temporal evolution of the particle numbers with different initial radius of curvatures:(a) ρ=30;(b) ρ=50;(c) ρ=60;(d) ρ=80.

图4 形核率随曲率半径的变化关系Fig.4.Nucleation rate versus initial radius of curvatures.

增强相的尺寸分布对材料性能具有决定性的影响,图5 统计了不同曲率条件下的晶核等效粒径分布图,横坐标为等效粒径与其均值的比值.从图5可以看出,曲率存在时第二相颗粒尺寸分布呈高斯分布.其中,曲率半径为80 和平直界面这两种情况下,晶核的粒径主要分布于均值左侧,这是因为形核率随着曲率半径的增大而增大,曲率半径较大时新相大量形核从而容易形成大量细小的第二相颗粒.当曲率半径为60 和80 时,晶核的主要尺寸分布较另外两组数据更宽,此时第二相颗粒尺寸不均匀情况将更加剧烈.因此,为了获得尺寸细小分布均匀的固相颗粒,可以在熔体混合过程中通过加压搅拌方式增大相界曲率来获得,见图5(a).

图5 不同界面曲率下的颗粒粒径分布 (a) ρ=30;(b) ρ=60;(c) ρ=80;(d)平直界面Fig.5.Particle size distributions with different curvatures:(a) ρ=30;(b) ρ=60;(c) ρ=80;(d) ρ=∞.

3.2 噪声强度对形核过程的影响

图6 为不同噪声强度条件下熔体相界处的原位反应形核过程,模型参数设置为kc=10,曲率半径ρ=60,过冷度参数为0.5.由图6 可知,形核位置仍然发生在两相界面处,即择优形核位置及新相成分并不随噪声强度的变化而改变.随着噪声强度增大,单位时间内新增晶核数目不断增大,同时晶核尺寸分布更加均匀.图7 为统计得到的形核率随噪声强度的变化图,可以看到形核率随着噪声强度的增大而先增大后趋于平缓,当噪声强度为0.05 时,形核率达到最大.这是由于在熔体中原位反应形核过程只出现在相界处,相界是由浓度从0.1 至0.9 平滑曲线所表征的区域,相界处原位形核意味着浓度需要达到某一个临界值才会发生形核.而噪声强度越大所提供的浓度起伏和结构起伏就越大,涨落越明显,使得满足形核条件的区域也就越多,所以在一定范围内(噪声强度小于0.05时)形核率会随着噪声强度的增大而增大.由于前期形成的晶核不断占据异质界面,使得利于新晶核形成的异质界面减少,受限于相界体积分数,当噪声强度达到一定程度后形核率将不再随噪声强度的增大而增大,见图7.

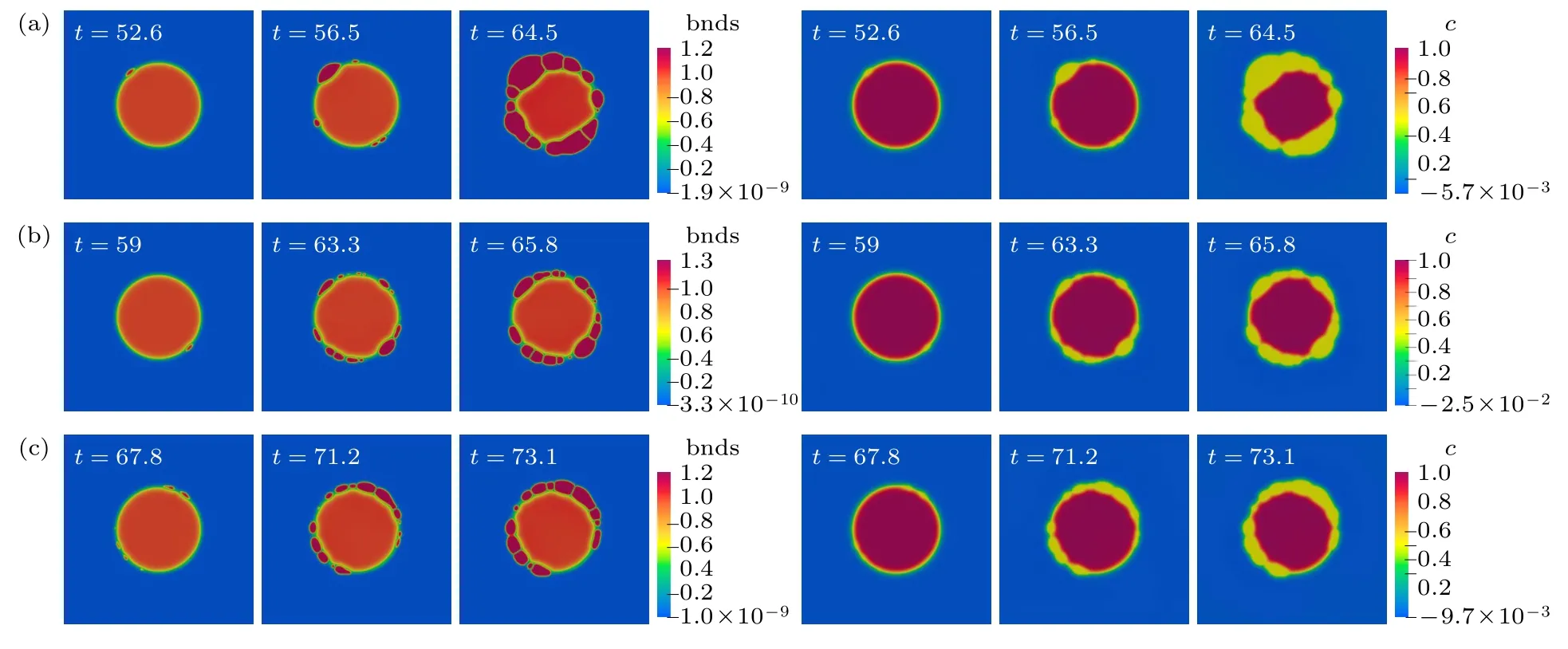
图6 不同噪声强度下的原位反应形核过程 (a) δ=0.03;(b) δ=0.05;(c) δ=0.07Fig.6.Snapshots of the in-situ reaction processes with different noise intensities:(a) δ=0.03;(b) δ=0.05;(c) δ=0.07.

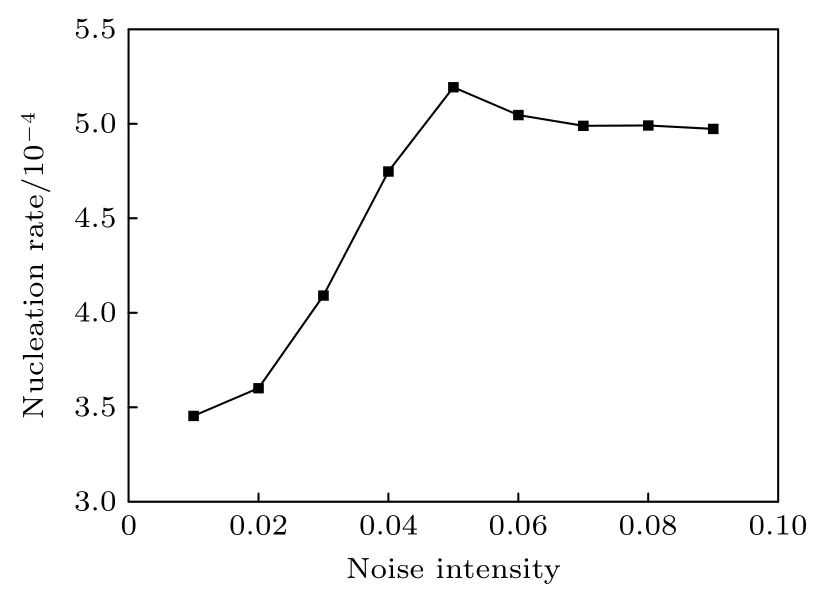
图7 形核率随噪声强度的变化关系Fig.7.Nucleation rate versus initial noise intensity.

进一步分析噪声强度对增强相颗粒尺寸分布的影响,如图8 所示.可以看出,颗粒尺寸分布为高斯分布,与图5 的统计结果相近.对比不同噪声条件下的尺寸分布可知,噪声强度为0.03 时,增强颗粒尺寸分布较其他两组结果更宽,此时颗粒尺寸均匀性较差,与图6 的模拟结果相符合.此外,进一步计算了平均颗粒半径,随着噪声强度增大,平均颗粒半径由57.78 降低到32.51.这一结果表明,随着噪声强度增大,增强相颗粒尺寸更加细小的同时,其尺寸分布也更加均匀.即在原位反应过程中可通过施加外界扰动来优化增强相的尺寸.

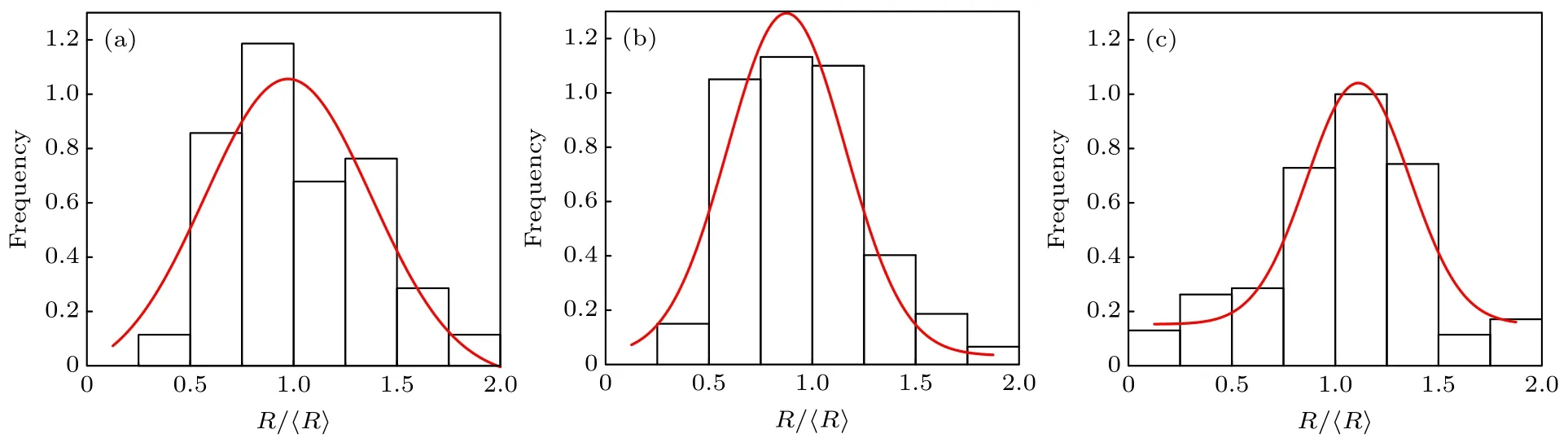
图8 不同噪声下的颗粒粒径分布 (a) δ=0.03;(b) δ=0.05;(c) δ=0.07Fig.8.Particle size distributions with different noise intensities:(a) δ=0.03;(b) δ=0.05;(c) δ=0.07.

3.3 过冷度对形核过程的影响

过冷度是影响相变过程的重要参数之一,其值对形核热力学、动力学过程均有着重要的影响.图9为不同过冷度参数(用A表示)条件下熔体相界处的原位反应形核过程,模型参数设置为kc=10,曲率半径ρ=60,噪声强度δ=0.01.从图9 可以看出,过冷度对择优形核位置无影响,并且随着过冷度的增大,熔体相界处的形核数增大.图10 为统计得到的形核率-过冷度关系曲线,可以看出,形核率随着过冷度的增大而先增大后减小.这是由于随着过冷度的增大,形核功将随之减小,形核过程更加容易进行,形核率增大;另一方面,无论是临界晶核的形成还是临界晶核的长大都伴随着液相原子向晶核的扩散和迁移,增加熔体的过冷度势必导致原子扩散能力的降低,进而影响形核过程,这一规律与经典形核动力学理论一致.

图9 不同过冷度参数下的原位反应形核过程 (a) A=0.5;(b) A=0.55;(c) A=0.65Fig.9.Snapshots of the in-situ reaction processes with different undercoolings:(a) A=0.5;(b) A=0.55;(c) A=0.65.

图10 形核率随过冷度参数的变化关系Fig.10.Nucleation rate versus undercoolings.

图11 为不同过冷条件下的颗粒粒径分布情况,可以看出,当过冷度参数为0.5 时,其尺寸为宽分布,这是由于该参数条件下形核率较低,原位反应中颗粒尺寸分布具有连续形核连续长大的特征,与经典形核过程的模拟结果一致[25],此时颗粒的平均尺寸为78.75.随着过冷度的增大,形核率不断增大,颗粒平均尺寸逐渐降低到42.53,这与经典凝固理论结果一致.此外,随着过冷度的增大,颗粒尺寸分布较过冷度0.5 时变得更加均匀.然而,相比不同噪声及相界曲率,过冷度对尺寸均匀性的调控作用较弱,即通过引入外界扰动和调控两熔束的混合过程(影响界面曲率)能够更加有效地调控增强相的颗粒尺寸分布情况.

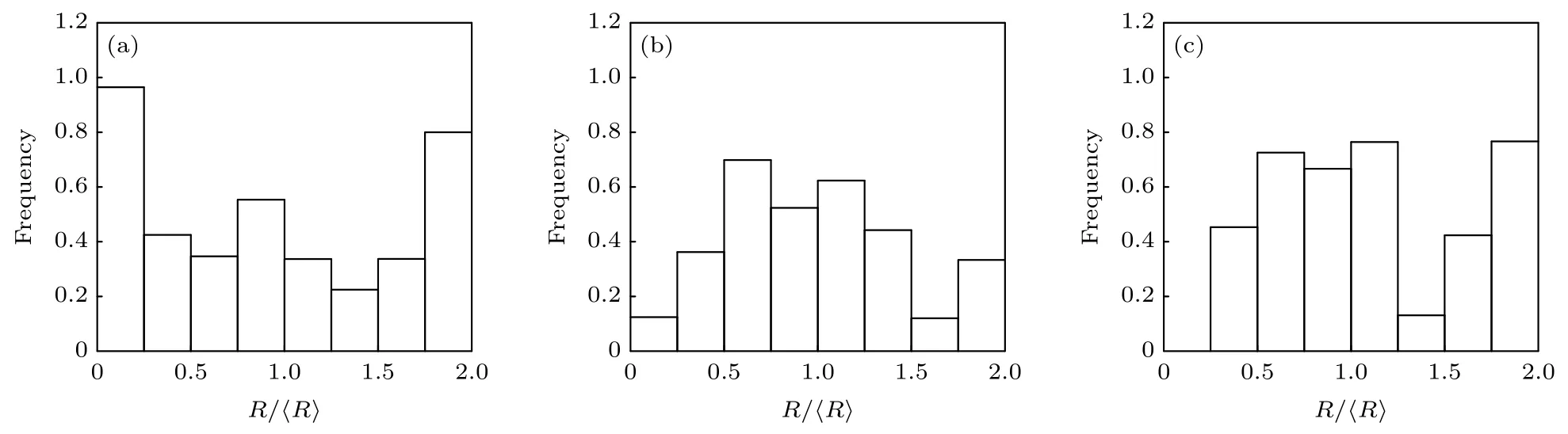
图11 不同过冷度参数下的颗粒粒径分布 (a) A=0.5;(b) A=0.55;(c) A=0.65Fig.11.Particle size distributions with different undercoolings:(a) A=0.5;(b) A=0.55;(c) A=0.65.

4 结论

本文建立了能够描述双熔体原位反应过程的相场模型,并采用该模型研究了相界曲率、噪声强度及过冷度对原位反应形核过程的影响.结果表明:界面曲率对形核的影响主要在晶核数目和晶核尺寸两个方面,界面曲率半径越大晶核数目越多且平均晶核尺寸越细小,这是因为曲率半径越大,异质界面面积越大,越有利于形核;一定范围内形核率会随着噪声强度的增大而增大,当噪声强度增大到0.05 时形核率将不再随噪声变化,此时晶核尺寸分布更加均匀;形核率随着过冷度的增大而先增大后减小.以上结论表明,本文所建相场模型的新相形核规律与经典形核理论相符合,同时原位反应过程与Guo 等[24]建立的理论模型一致,这充分证明了新模型的有效性,为进一步研究原位反应动力学过程奠定了基础.