基于衍射理论的哈达玛编码光谱成像数据重构*

刘文龙 刘学斌 王爽 严强强†

1)(中国科学院西安光学精密机械研究所,中国科学院光谱成像技术重点实验室,西安 710119)

2)(中国科学院大学,北京 100049)

哈达玛变换光谱成像技术是一种在不牺牲分辨率的情况下,通过多通道复用的方法增加光学系统光通量,使得系统信噪比显著高于传统成像的新型计算光谱成像技术.本文针对系统成像过程中数字微镜器件衍射造成的图像降质问题,建立了基于标量衍射理论的哈达玛编码光谱成像图谱数据退化模型,提出以Lucy-Richardson (L-R)算法为核心的重构数据修正算法,提高重构数据立方体的图像质量和光谱精度.通过对成像过程的模拟和重构算法的仿真实验,数字化生成了系统成像衍射降质的物理过程,并验证了本文所采用修正方法的有效性.经过L-R 修正之后的复原数据立方体的光谱角距离评价结果为0.1296,图像相似度评价因子优于0.85,相比修正前的重构数据质量有较大提升,表明算法对哈达玛编码光谱成像数据的重构及修正具有较好的效果.

1 引言

光谱成像作为一种有效信息获取方式,由于其获得的二维空间信息与一维光谱信息的数据立方体,能同时反映探测目标的几何特征及光谱特征,更加准确地解译探测目标的属性,而被应用在医学成像、环境遥感、天文观测等众多领域[1].孔径编码作为一种新型调制方式,代替了传统成像光谱仪的狭缝[2],形成多路复用的多通道凝视光谱成像模式,使得系统能够获得高信噪比信号[3,4].孔径编码光谱成像的编码方式可分为基于压缩感知的稀疏编码和基于完全采样的完备编码[5,6],相比于压缩感知的稀疏编码,完备编码方案无需考虑信号的稀疏性,其数据重构算法简单,信息几乎无损失.其中,哈达玛编码从数学上被证明为完备编码的最优方案之一.由于系统中调制编码对象不同,可将哈达玛编码光谱成像技术(Hardmard transfer imaging spectrometer,HTIS)分为空间编码和光谱编码两种技术方案,分别对应了单色散哈达玛编码光谱成像技术(SD-HTIS)和双色散哈达玛编码光谱成像技术(DD-HTIS).

哈达玛编码光谱成像仪最为核心的器件是调制编码模板,早期主要采用机械刻蚀的掩膜板.相比机械模板,DMD 具有更高的变换速度和分辨率.美国Sandia 国家实验室第一次将数字微镜器件(digtial micromirror devices,DMD)用于编码成像系统中,验证了采用DMD 器件的编码光谱成像技术的可行性[7].美国杜克大学使用DMD 作为调制器件,研制了孔径编码快照成像系统,即压缩感知成像系统,并进行了单色散和双色散孔径编码光谱成像系统的数据重构[8,9].孔径编码光谱成像作为一种计算光谱成像技术,具有诸多传统光谱成像技术不具备的优势,但在数据使用过程中,极大程度上依赖于高精度的光谱和图像重构算法.DMD 作为微纳器件,对系统装调精度有着极高的要求,另外,其自身较强的衍射效应,也给孔径编码成像系统带来了能量偏移、响应不均匀、衍射降质等问题,造成重构数据立方体的图像和光谱信号失真.因此,数据立方体的高精度重构是孔径编码光谱成像技术走向应用所需要解决的关键问题之一.Streeter 等[10]和Galvis 等[11]通过优化系统设计的方式来解决提高成像质量,提出采用照明光源的设计方案来修正基于DMD 的Hadamard变换成像光谱仪在采集过程中产生的能量偏移误差.Stenven[12]和David[13]借助DMD 器件在实验室搭建了一套可见光波段的孔径编码光谱成像系统,用于探索DMD 自身的衍射效应对系统成像的影响,并提出在光路前级添加第二块DMD 作为衍射预补偿的新思路,针对系统存在的问题,在系统设计和算法设计两方面不断演进解决方案.胡炳樑等[14,15]通过辐射标定的方式,结合后处理算法对系统编码像素点错位导致的能量偏移及系统存在的辐射响应不均匀进行了修正.Chi 等[16−18]认为光学系统的点扩散函数和光阑的非均匀照明是造成系统解码错误的主要来源,通过对光学系统的编码过程进行了标定,在此基础上采用Gold 反卷积的方式对编码矩阵进行了修正,消除了编码数据相邻空间的串扰.

光谱数据立方体的高精度重构是哈达玛编码光谱成像技术亟须解决的问题.在上述研究工作的基础上,本文针对哈达玛孔径编码光谱成像过程中系统衍射效应导致的点扩散弥散引起的数据降质问题[19,20],从成像机理上开展了衍射效应的正向传输过程的模拟.结合了光谱成像系统多通道编码的思想和菲涅尔标量衍射效应对光学系统的降质的物理模型,开展了哈达玛孔径编码光谱成像系统数据降质过程的仿真实验.针对光学系统实际成像过程中的点扩散效应对数据重构的影响,提出了基于Lucy-Richardson (L-R)的单谱段图像修复算法,其中,L-R 算法能够按照泊松噪声统计标准对给定点扩散函数的退化图像进行反卷积迭代推演计算,充分考虑了信号的统计涨落特性,经过一定次数的迭代计算后可得到接近理想清晰图像的最大似然估计值[21−23].通过对修正后的信号进行哈达玛解码运算,实现对编码光谱数据立方体的高精度重构.

2 哈达玛编码光谱成像数据重构原理

2.1 成像原理和重构理论

相比传统光谱成像技术而言,单色散哈达玛编码光谱成像技术在一次像面位置用多通道的编码模板代替了狭缝,通过数字微镜器件对空间信号进行调制,实现对信号的编码.其光学系统的成像原理示意如图1 所示,系统包括前置物镜、编码元件、准直光路和色散元件、二次成像镜和探测器焦面.在HTIS 中,前置物镜和一次像面相当于一台普通的相机,获取目标的全波段的图像信息.一次像面位置的DMD 通过微镜在“0”和“1”之间翻转对目标的空间信息进行选通和关闭,实现信号的编码.继而,由系统中的准直镜对编码后的空间图像进行准直,再通过色散光栅对各个谱段图像进行重排,其中相邻单谱段图像编码后的空间信号在光栅的作用下平移一个像素的位置.不同谱段的相邻空间位置的信号在同一探测器像元上叠加,获得最终的成像结果.

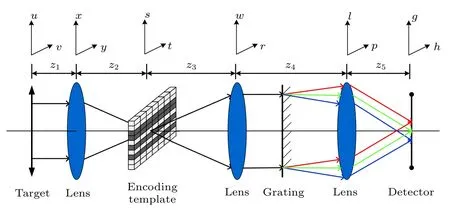
图1 空间调制型哈达玛编码光谱成像系统光学结构示意图Fig.1.Schematic diagram of SD-HTIS optic structure.

HTIS 对目标的图像和光谱信息的编码过程如图2 所示.输入目标的全谱段信号经过编码模板和色散元件的调制作用,各个谱段信号在光谱维按照编码规则进行叠加,通过对编码模板多次变换能够实现信号的完备编码,使得信号叠加满足向量方程.采用哈达玛编码,保证了信号矩阵的非奇异性,使多波段信号可以根据编码模板信息和多次采样压缩信号在数学上能够被有效求解.

在单色散哈达玛编码光谱成像技术中,每一次成像,相当于光学系统实现了一次相邻空间位置的不同谱段信号的编码叠加,获得一组包含多个未知量的方程.可以表示为

其中n指探测器像元行位置,yn表示探测器像元响应,L表示编码阶数,i表示谱段数,hi表示对应i谱段信号的编码,xn+1−i,i表示对应n+1–i像素对应空间位置处i谱段的信号.经过L次变换构成编码向量空间记为H,编码的光谱信号记为X,探测器接收到的信号记为Y,成像系统的数学模型可以表达为[24]

传统哈达玛矩阵并不适用于工程应用,一般在光学系统中采用Hadamrd 矩阵的变体Sylvester矩阵作为编码矩阵,其特点是矩阵的不同行是由首行向量进行平移得到的[25,26].对于一个7 阶哈达玛编码的光谱成像系统,若S循环矩阵的首行元素为[s1s2s3s4s5s6s7];xij为信号在i位置处j谱段的原始信号,其中j∈[1,2,3,···,7];表示i位置第r次成像得到的探测信号,其中r∈[1,2,3,···,7].基于该编码矩阵的成像可以通过下式表示:

左移S矩阵具有以下特点:

1)Si=[si,si+1,···,sN,s1,···,si−1],其中i是指矩阵的行序列;

2)如果Sij=1,则=1;如果Sij=0,则=−1.且S和S′之间满足S−1=,其中i表示S矩阵的行序号,j表示S矩阵的列序号,L表示编码模板的阶数,i,j=1,2,3,···,L.

哈达玛编码光谱信号的重构是对线性方程的求解.考虑到S矩阵逆变换的特点,光谱信号可通过以下方程进行重构:

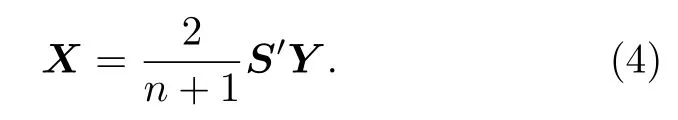
2.2 基于标量衍射理论的信号修正理论

相比传统的扫描型光谱仪,哈达玛编码光谱成像技术通过多通道编码原理,将各个谱段的信号在探测器上进行叠加,使得信号具有较高的信噪比.这一理想编码过程可以用如下公式表示:

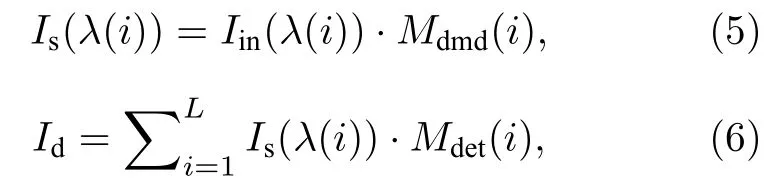
其中,系统光谱谱段数和编码模板阶数含义一致,用L表示,Mdmd(i)为λ(i) 波段对应的DMD 模板的掩膜,Iin(λ)为输入目标的单个谱段信号,Mdet(i)为探测器对应的掩膜,Is(λ) 表示经过DMD 调制的λ波段的编码图像,Id表示探测器上接收的多个谱段编码图像的叠加.

编码成像的原理是通过空间光调制器件使得探测器上接收到的信号被打开或者彻底关断,从而通过“1”和“0”实现对信号的编码调制.但实际成像过程中,由于DMD 的微镜片尺寸很小,在调制编码过程中产生的衍射效应使系统点扩散函数弥散较为严重,使得编码过程中探测器上接收到编码为“0”的信息受到编码为“1”的信息的干扰,这对于编码图像造成较大的影响,编码光谱数据立方体的复原结果和原始数据比较有极大的降质,造成探测目标的信息失真.针对这一问题,基于标量衍射理论对系统光路传输进行推演,建立系统的成像降质过程的数理模型.

在哈达玛编码光谱成像系统中,(x,y)目标的λ波段经过z1距离传输并经过前置镜相位调制后的衍射光场U(u,v,x,y,λ)可以表示为

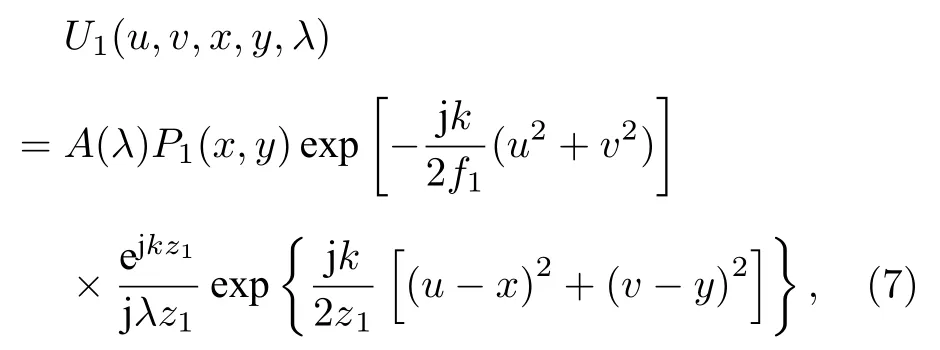
其中k=2π/λ,A(λ)为λ波段对应信号强度,P1(x,y)表示前置物镜孔径,f1为物镜焦距.U(u,v,x,y,λ)经过z2距离正向传播至(s,t)平面的光场分布U2(s,t,x,y,λ)为

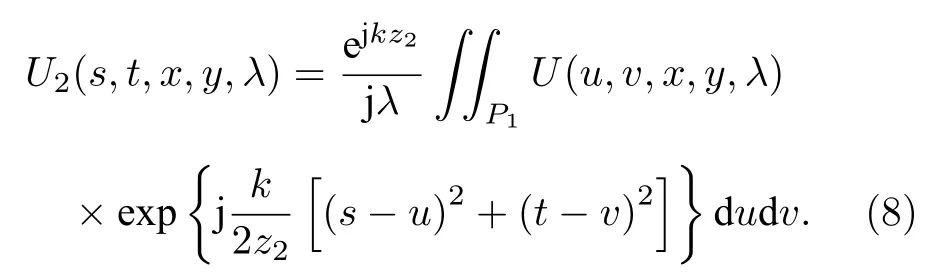
U2经过DMD 调制后在(w,r)平面上的光场分布表达如下:

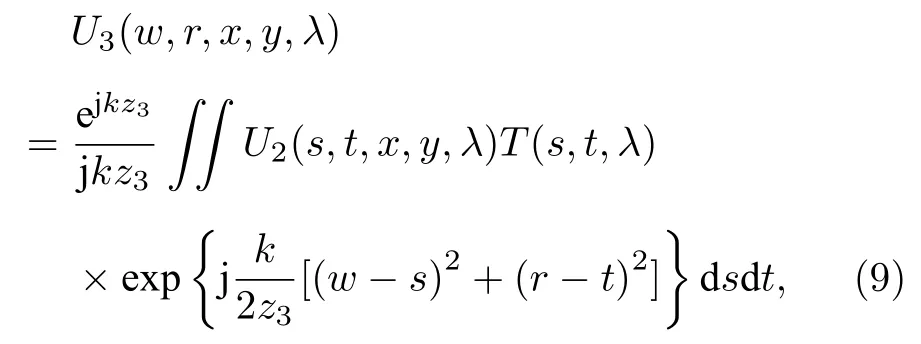
其中T(s,t,λ) 表征DMD 的数理模型,d为单个微镜边长,则微镜的数学表达如下:

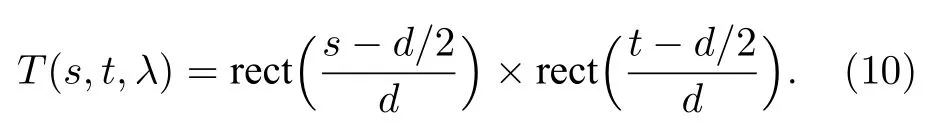
哈达玛孔径编码图像是基于单波段信号的编码叠加实现的,光栅的分光作用通过不同波段的像对应的几何位置进行表征,即不同波段的图像在(l,p)平面上的位置受到波长的影响,最终的(l,p)平面上的光场U4(l,p,x,y,λ)为

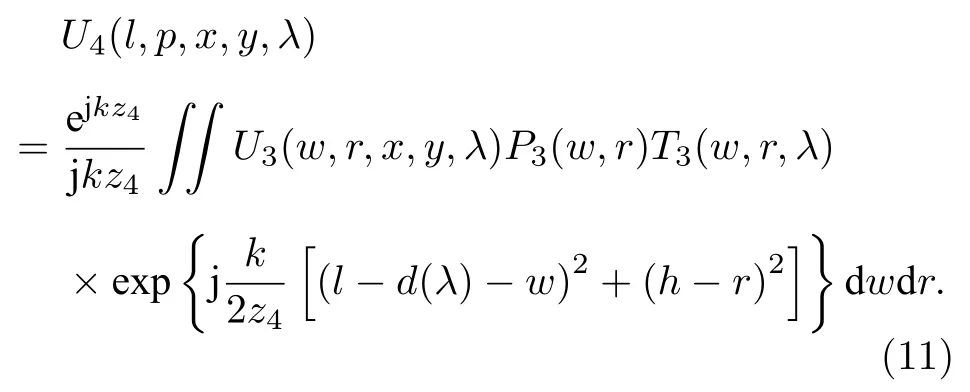
式中T3(w,r,λ)和P3(w,r)分别表示(w,r)平面位置处透镜的透射调制函数和孔径函数.定义(l,p)平面处的透镜的调制函数和孔径函数分别为T4(w,r,λ)和P4(w,r),最终探测器像面上的光场复振幅Ud(g,h,x,y,λ)的分布为

记哈达玛编码光谱成像系统单个谱段成像过程中的点扩散调制函数为Fpsf,

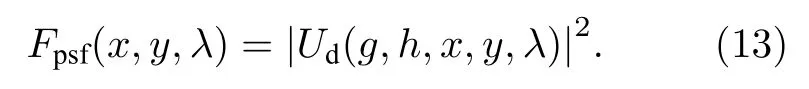
通过上述模型可以计算物点在探测器面对应的点扩散函数,进而通过点扩散函数和对应物点强度信息的卷积计算,获得目标编码调制的单谱段衍射图像:

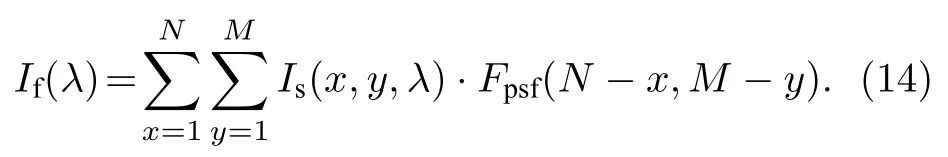
此时,探测器上得到降质后的编码图像Id可表示为

基于标量衍射模型的哈达玛编码光谱成像系统的构建,为系统成像的理论分析奠定了基础.从物理光学的角度进行分析,当光学系统中的孔径较小时,会产生较为严重的衍射效应,即点扩散函数受到系统中微小孔径衍射效应的影响.在基于DMD 的孔径编码光学系统中,系统成像过程中将DMD 衍射带来的降质因子通过点扩散函数和编码调制信号的卷积向系统的终端信号进行了传递,从而导致了成像信息频率混叠和图像降质.因此,要消除衍射效应对系统复原光谱数据的影响,需要对受衍射影响的图像数据进行频域上的分离,在此基础上,对单谱段图像信号进行修正.通过对(15)式进行逆矩阵操作,即可实现单谱段信号分离,获得单谱段图像信息.

(16)式从数学层面上解释了单波段图像降质过程,本质是衍射效应下生成的点扩散函数和真实信号强度信息卷积.而通过卷积对灰度图像进行修正的研究已有诸多成果.L-R 图像修复算法是一种基于卷积因子盲估计的退化图像反卷积复原优化算法.L-R 算法认为,如果模糊图像g是由原始图像f和模糊因子卷积得到,假定图像各个点之间相互独立,根据泊松分布统计模型,g和f的条件概率分布可用以下公式表示:

那图像中g和f应满足条件:

其中g=h ∗f,g表示采集信号,f表示输入信号,h表示信号的传递函数.(17)式中p(g|f) 的约束条件为(18)式,为获得最大概率,将(17)式两边对数化后进行梯度运算:

由(19)式解得

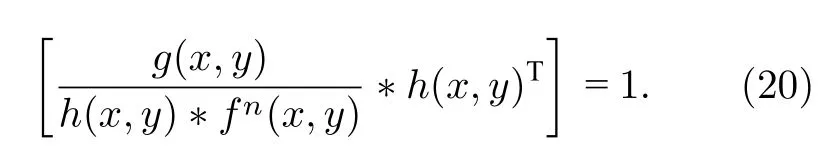
最终得到的优化迭代函数为

上述优化过程能够实现对降质图像的修复,通过L-R 算法实现了对编码单谱段图像的修正,让其更加接近理想成像结果.在此基础上,将修复后的图像重新进行压缩编码,获得修正后的编码图像.

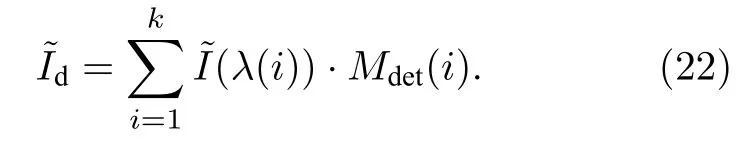
通过上述过程对完备编码的多帧图像进行修正,根据(4)式对光谱数据进行重构,获得目标的数据立方体.

3 实验结果和讨论

3.1 降质分析

上述数理模型从理论上对哈达玛编码成像过程及数据降质问题进行了解释说明,并从机理上提出了数据修正算法.本节在系统数理模型的基础上设定哈达玛编码光谱成像系统的参数,并根据参数进行成像系统的仿真实验.实验参数如表1 所列.

表1 哈达玛编码光谱成像系统的参数表Table 1.Parameters of the Hardmard transfer imaging spectrometer system.

表1 中,f1为物镜焦距,f2为准直镜焦距,f3为成像镜焦距,z1=1000 m,z2=f1,z3=f2,z4=f2+f3,z5=f3;D1为物镜孔径,D2为准直镜大小,D3为成像镜大小,D4为探测器像面大小;单个DMD 微镜的尺寸为10.8 µm,单个探测器像元大小为30 µm,光谱仪的光谱范围为3.7—4.8 µm,分为7 个谱段.

首先,在不考虑成像系统像差和成像衍射等因素影响的情况下,开展哈达玛编码成像仿真工作,以AVIRIS 数据为仿真输入数据,仿真7 阶哈达玛编码光谱成像过程,并针对10 dB 噪声的信号进行重构,结果如图3 中的伪彩色图所示,其中图3(a)为原始输入数据,图3(b)为编码得到的多帧图像,图3(c)为重构的数据立方体.

图3 AVIRIS 数据仿真生成及复原光谱数据 (a)原始输入数据;(b)编码生成的多帧图像数据;(c)复原后的光谱数据立方体Fig.3.Simulation of AVIRIS data and the restoration spectral data:(a) Original input data;(b) multi-frame image data generated for encoding;(c) restored spectrum data cube.

通过图像相似度因子对重构图像进行评价,将重构数据立方体的单谱段图像和原始输入图像进行比较,两者的相似度因子的评价结果如表2 所列.

取原始数据和复原数据的物点光谱曲线进行比较,原始数据和复原光谱数据同一目标的光谱曲线进行评价,光谱角距离评价因子的均值为0.006,反演数据和原始数据几乎一致.上述仿真结果证明,在不存在衍射和系统像差的情况下,仅由系统噪声对数据重构产生的影响较小.

实际成像过程中,哈达玛编码光谱成像过程中受到系统中微纳光学器件的影响,造成图像结果降质,根据预设的光学系统参数,在衍射成像模型的基础上开展仿真实验,通过(13)式计算获得目标点在探测器表面的点扩散函数,图4(a)表示得到的像点扩散函数形状;图4(b)表示沿横向过像点中心点位置的归一化的强度分布曲线,其中横向表示像素点序号,纵向表示各个像素点上的信号强度和输入信号强度的比值.

归一化的系统点扩散分布如图4 所示,可以看出,受衍射效应的影响,系统的能量弥散到多个探测器像元之上,使得生成的压缩编码图像质量下降.根据仿真实验结果直接重构得到的数据立方体的光谱角距离达到了0.502,相比系统噪声带来的影响,数字微镜器件衍射对数据重构的影响更为严重.因此,减小和消除系统的衍射降质影响是哈达玛编码光谱成像数据重构急需解决的问题.

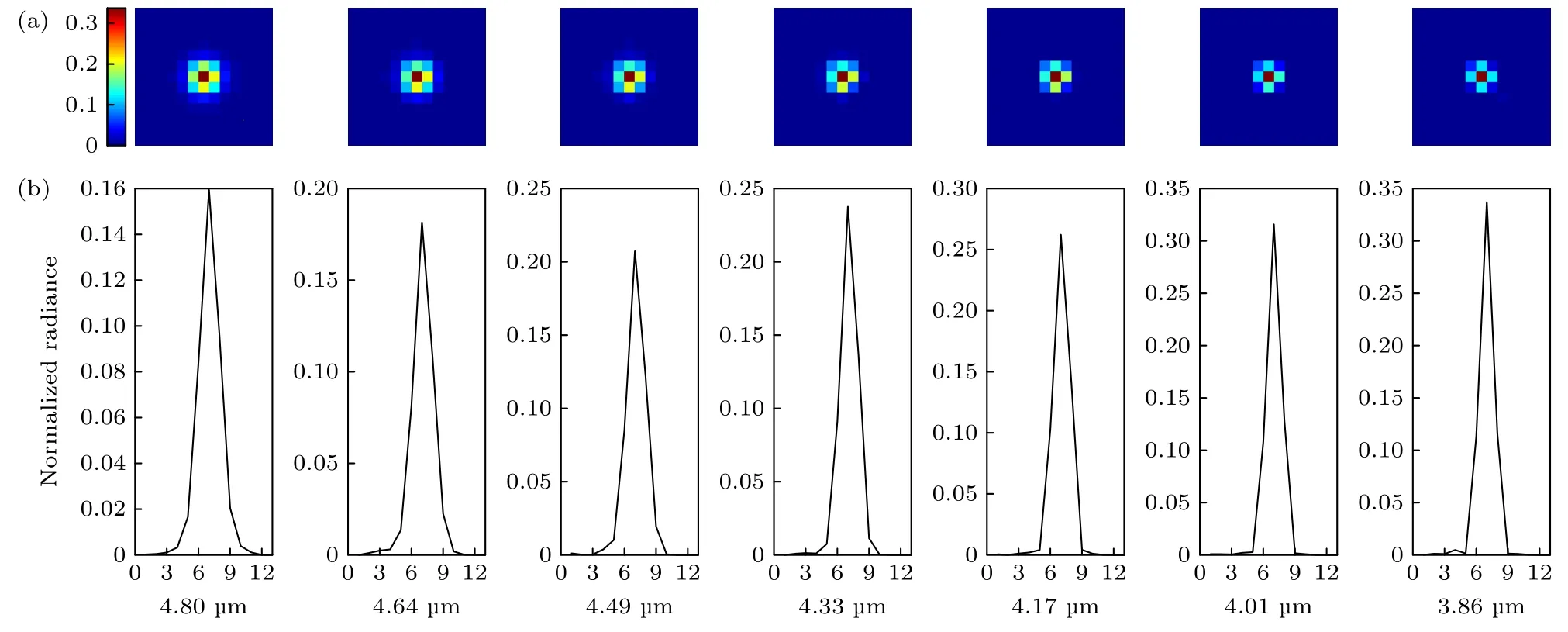
图4 归一化的系统点扩散函数分布图 (a)像点的点扩散函数图;(b)归一化的像点强度分布曲线Fig.4.Normalized system point spread distribution diagram:(a) Point spread function diagram of image spot;(b) distribution curve of normalized image point intensity.

3.2 衍射图像修复仿真实验与数据分析

根据理论降质模型,首先对编码图像进行分解,得到图像的多个谱段的编码信息,通过L-R 算法对分解得到的单谱段图像进行修复.由于光学系统的点扩散函数更接近于高斯分布,因此修复算法中用于逆卷积的核函数采用高斯核,本实验中采用的高斯滤波器维度为11×11,经过优化迭代计算,最终采用的滤波器标准值为0.730.经过上述单谱段图像的修复之后,重新对各个谱段信息进行压缩计算,获得修正后的编码图像如图5 所示.和修正前的图像相比,修正后图像的对比度和图像的细节信息得到较大提升,图5 中红色框图标记位置两者对比十分明显.

图5 Hadamard 编码单谱段图像 (a)衍射降质图像;(b)复原修正图像Fig.5.Encoded single-spectrum image:(a) Image with the influence of diffraction;(b) image optimized by the L-R repair algorithm.

以理想编码图像为基准,对受衍射影响的编码图像和经过修正的编码图像进行比较,相似度因子评价的结果如表3 所列.相比受衍射影响的图像,修正后的数据更加接近理想的编码图像.这一结果证明了L-R 算法能够有效实现对降质数据的修正,提升数据重构的质量.

表3 受衍射影响的编码图像和经过修正的编码图像的相似度因子评价Table 3. Similarity factor evaluation of uncorrected coded image and corrected encoded image.

在此基础上,通过(4)式实现对数据立方体的重构,图6 分别给出了原始输入数据立方体、未经过衍射修正的数据重构的立方体和修正后的数据重构的数据立方体.

图6(b)和图6(c)直观地反映了修正前后重构的数据立方体的质量.对上述复原光谱数据立方体的准确性进行评价,将数据立方体的各个谱段和输入光谱图像进行比较,相似度评价结果如表4 所列.

表4 未修正SSIM 与修正后SSIM 的相似度评价Table 4. Similarity evaluation of uncorrected SSIM and corrected SSIM.

随机选取图6 数据立方体中3 组光谱曲线进行比较,结果如图7 所示,其中横坐标位光谱谱段数,纵坐标表示数字信号的灰度值.可以看出,修正后的光谱数据和原始输入数据更加接近,而未经过修正的重构光谱数据和原始输入偏差较大.以输入数据立方体为对照数据,分别对直接重构的数据立方体和经过修正后复原的数据立方体包含的全部光谱信息的光谱角距离进行评价,其中直接对衍射编码复原谱角距离均值为0.508,而经过L-R 修正之后的复原得到的数据立方体的光谱角距离均值为0.130.

图6 不同谱段光谱图像 (a)原始输入和理想复原图像;(b)经过衍射效应影响复原的多谱段图像;(c)经过L-R 修正后复原的多谱段图像Fig.6.Spectral images of different bands:(a) Original input and ideal restoration image;(b) multi-spectral image restored by diffraction effect;(c) multi-spectral image restored after L-R correction.

上述实验说明,空间调制型哈达玛编码光谱成像系统中,衍射是造成重构数据失真的主要因素.在哈达玛编码光谱成像系统衍射模型的基础上,通过L-R 算法能够有效地实现信号的修正,提高重构信号的质量.

4 结论

本文针对多通道孔径编码光谱成像技术中的数据衍射降质问题,结合哈达玛编码光谱成像的机理和标量衍射理论,建立了哈达玛编码光谱成像的数理模型,通过对模型的分析,发现哈达玛编码光谱成像系统中的衍射效应是导致系统重构数据退化严重的主要因素,并构建了基于点扩散函数的哈达玛编码光谱数据的退化模型.在此基础上,设计了一种基于L-R 算法的数据逆卷积重构算法,该算法结合了光谱成像系统的多通道编码的思想和光学系统实际成像过程中的点扩散响应.算法首先编码压缩的图像进行逆向分解,获得多个谱段的编码图像,针对不同谱段的图像使用L-R 算法对降质图像进行迭代优化,降低了衍射降质因子对图谱数据的影响,从而提高了重构光谱数据立方体的精度.该方法从数理层面上开展了对系统重构数据降质因素的分析,并通过降质模型,实现了对复原图谱数据的修正.这项工作提高了采用DMD 作为编码器件的哈达玛光谱成像系统的数据立方体重构精度,为孔径编码光谱成像在多学科的应用研究上发挥重要作用.