改进人工势场的智能车避障算法研究
孙伶玉,付主木,b,陶发展,b,司鹏举,b,宋书中,b
(河南科技大学 a.信息工程学院;b.河南省机器人与智能系统重点实验室,河南 洛阳 471023)
0 引言
由于汽车普及率的提高和复杂的交通参与者构成,车辆安全行驶变得愈加困难[1-2],故智能车的研究受到人们的广泛关注。通过研究路径规划算法,为智能车辆提供安全、可靠和平稳的避障路径,实现车辆在不同环境下的精准避障[3-4],已成为当下研究的重点问题。
现有的路径规划算法主要分为全局路径规划算法和局部路径规划算法。全局路径规划算法主要包括A*算法[5]、D*算法[6]、蚁群算法[7]和遗传算法[8];局部路径规划算法主要包括人工势场(artifical potential field,APF)算法[9-11]、Bug算法[12-13]和快速搜索随机树算法[14-15]。在实际应用中,通常将几种规划算法结合起来,以达到所需效果。
针对复杂交通场景下智能车辆的路径规划问题,文献[16]提出了人工势场算法,其结构简单、数学描述方便、计算量小,可实现实时路径规划。然而,该算法本质上仍属于局部路径规划算法,导致其存在目标不可达和易陷入局部极值等固有问题[17]。
目前,部分学者针对人工势场存在的缺陷进行了一系列的研究。文献[18]提出了基于改进势场函数的扇区划分方法,在局部极值点附近增加虚拟障碍物,通过调整斥力场分布,使车辆可以驶出局部极值。文献[19]提出一种基于人工势场的回归搜索方法,利用虚拟局部引力和斥力,消除传统人工势场算法存在的局部极小值问题,获得最优路径。文献[20]提出一种势场填充策略,使用电位填充方法,在目标不可达与局部极小值的位置设置一个额外的电位场,将机器人拉离局部极小值以解决人工势场存在的缺陷。在上述研究中,车辆始终被视为没有质量的粒子,同时未考虑车辆运动学参数对路径规划效果的影响,因此在更为复杂的实际行驶环境中无法保证车辆安全行驶至目标位置。
因此,本文将车辆运动学参数和质量因素引入人工势场算法,设计自适应斥力函数,并结合Bug算法,设计了一种新的智能车辆避障路径混合规划方法。为验证算法的有效性,在MATLAB软件环境下对本文所提算法进行计算机仿真研究,并通过搭建智能车试验平台验证算法的实际避障效果。
1 模型建立
1.1 改进人工势场算法
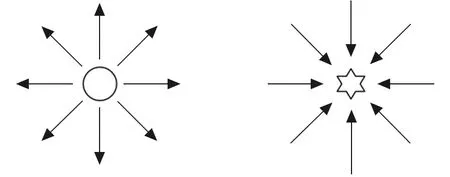
(a) 障碍物的斥力 (b)目标点的引力
人工势场算法是现今广泛应用的一种路径规划算法,其基本思想是将车辆的运动映射到人为设定的抽象势场中,把实际环境具体化成人造势场。人工势场算法规划的路径平滑、执行效率高、计算量小,但是存在目标不可达和局部极值等缺点[21],故本文采用APF框架改进人工势场算法,以规划合理有效的行驶路径。其中,车辆在抽象势场中的受力情况如图1所示(箭头方向即受力方向)。
引力势场由目标位置产生,引导车辆向目标位置移动产生,其势场函数为:
(1)
车辆在引力势场中受到的吸引力Fatt可以表示为:
Fatt(q)=-Uatt=ζρ(q,qgoal),
(2)
其中:ζ为引力势场增益因子;ρ(q,qgoal)为当前点q与目标点qgoal之间的欧氏距离。引力的方向是从车辆的当前位置指向目标位置。
斥力势场是由障碍物产生的。当车辆靠近障碍物时,会受到排斥力的影响,随着车辆与障碍物之间的距离变短,排斥力会增加。斥力势场函数如下:
(3)
车辆受到的斥力为Frep,其表达式为:
(4)
其中:ρ(q,qobs)为q点与其最近障碍物的距离;η为斥力增益常量;ρ0为障碍物的作用阈值范围。
在以往的人工势场算法研究中,通常将车辆固定为粒子,忽略车辆自身的质量和速度。而在实际应用中,不能忽视车辆的质量和速度对势场产生的影响。因此,通过改进人工势场的斥力函数,在原有函数的基础上考虑车辆运动学参数,使改进的算法更适合实际环境。
考虑到规划路径的安全性、稳定性和路径长度,可以通过在人工势场的斥力场函数中加入调节项kmmvτ改进斥力场函数,其中,km为调节系数,kg-1;τ为调节参数。经仿真试验可得,当τ为2时,仿真效果最佳;m和v分别为车辆的质量和速度。通过一系列仿真试验,得到km的合适变化范围。改进后的斥力势场如下[11]:
(5)
其对应的斥力为:
(6)
随着车辆向目标点移动,车辆将受到吸引力势场和斥力势场的共同影响[11]。
车辆的合力势场函数为:
U(q)=Uatt(q)+Urep′(q)。
(7)
因此,合力F可以表示为:
F(q)=-U(q)=Fatt(q)+Frep′(q)。
(8)
1.2 算法验证
本文利用MATLAB软件对改进的规划路径算法进行仿真验证。对比分析传统的人工势场算法与改进的人工势场算法的区别,验证改进后的人工势场算法对所规划行驶路径的安全性的影响。其中,相同质量、不同车速条件下的仿真结果如图2a所示,相同车速不同质量条件下的仿真结果如图2b所示。

(a) 质量相同车速不同的仿真结果 (b) 车速相同质量不同的仿真结果
图2a和图2b中蓝色轨迹是传统的人工势场算法所规划的行驶轨迹,车辆质量m为10 kg,车辆速度v为100 cm/s,发现传统人工势场算法所规划的行驶路径灵敏度较弱,距离障碍物较近,安全性没有保障。图2a中红色轨迹与绿色轨迹为改进的人工势场算法在车辆质量相同、车速不同情况下的仿真结果,红色轨迹的车辆质量m为10 kg,车辆速度v为300 cm/s,绿色轨迹的车辆质量m为10 kg,车辆速度v为500 cm/s。对比图2a的仿真结果可以发现:当车辆质量不变时,车速越大,车辆受到障碍物的斥力越大,车辆对斥力势场的敏感度越高,所规划的行驶轨迹更加安全可靠。图2b中红色轨迹与绿色轨迹为改进的人工势场算法在车速相同、车辆质量不同情况下的仿真结果,其中,绿色轨迹的车辆质量m为100 kg,车辆速度v为100 cm/s,红色轨迹的车辆质量m为500 kg,车辆速度v为100 cm/s。对比图2b的仿真结果可以发现:随着车辆质量的增加,车辆受到障碍物的斥力会增大,同时车辆的惯性也会增强,故为了提高车辆行驶过程中的安全性,应该选择合适的车辆质量。根据图2仿真结果对比发现:当车辆靠近障碍时,改进的人工势场算法可以快速感知障碍物的位置,安全避开障碍物。改进后的算法所规划的行驶路径更加平滑、安全、鲁棒性更强。
2 混合算法设计
车辆在虚拟势场中受到多个障碍物的斥力共同作用,一般情况下,车辆可以避开障碍物抵达目标位置,但是当地形复杂、障碍物较多时,车辆极有可能在某一位置陷入局部极值,无法继续前行。针对该类复杂场景,本文采用算法混合的方式,引入Bug算法以弥补APF算法的缺陷。因为Bug算法是一种局部优化算法,传感器只需要获取周围环境的局部信息,其在线成本低,速度快且效果显著。故提出APF-Bug混合算法,以解决复杂静态环境与动态环境下车辆的实时路径规划问题。本文使用复杂的障碍物轮廓地图与动态超车地图,验证所提算法的适应性和有效性。
两种算法相结合的关键位置是APF算法中合力为零的点。当车辆到达该点时,APF算法将切换为
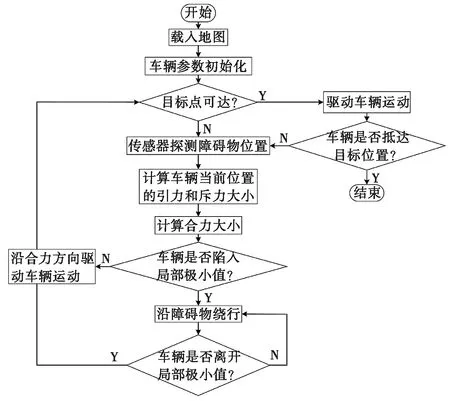
图3 APF-Bug混合算法流程图
Bug算法,旨在将车辆的位置调整到Bug算法的主线上。车辆移动到主线上之后便沿着主线移动,当遇到障碍物时,车辆便沿着障碍物的边界移动直到车辆再次触及主线。此后,车辆便可以逃出局部极值点,Bug算法将切换回人工势场算法,使车辆快速高效地移动到目标位置。判断车辆是否陷入局部极值,采用以下条件:
(9)
当满足上述条件时,车辆被判断为遇到局部极值点[10]。其中,ε是一个很小的正数,代表着车辆的合力接近于0。对复杂障碍物环境下的地图进行可视化,验证APF-Bug混合算法的有效性。整个算法流程如图3所示。
3 仿真验证
3.1 混合算法的仿真验证
利用MATLAB软件对混合后的算法进行仿真验证,将障碍物环境在模拟地图中可视化。模拟地图的分辨率为500 dpi×500 dpi,地图包含一个起始位置x(50,50)、一个目标位置x(450,450)和多个静态障碍物。为了突出混合算法的优越性,将APF算法、Bug算法和APF-Bug混合算法所规划的行驶路径分别在复杂的地图环境中仿真运行,其仿真效果如图4所示。不同算法的仿真结果如表1所示。

(a) APF算法(b) Bug算法 (c) APF-Bug混合算法
图4中,黑色填充区域表示障碍物。图4a为APF算法所规划的车辆行驶路径,可以发现APF算法所规划的行驶路径难以逃脱局部极值,并且车辆易与障碍物相撞,避障失败。图4b为Bug算法的避障路径图,仿真路径可以发现车辆顺利抵达目标位置,但从表1的仿真结果可知,车辆从起点到目标点的迭代步数较多,用时较长,导致规划过程中的成本相对较高,使得该算法难以适用于实际应用中。图4c为APF-Bug混合算法所规划的车辆路径图,从仿真路径和表1的仿真结果可以看出:车辆可以安全快速地抵达目标位置,并且相对于Bug算法,APF-Bug混合算法的迭代步数与时间明显降低,故改进算法的效果相对于两个单独的算法有明显提升。
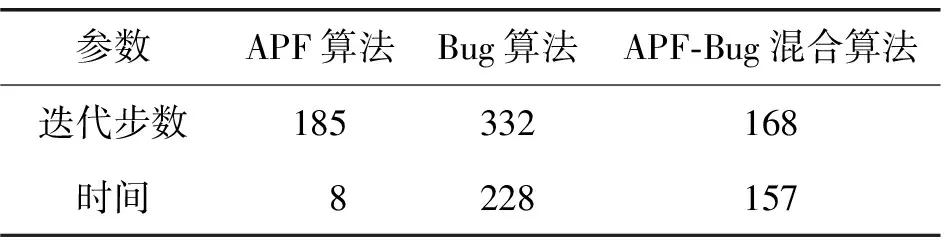
表1 不同算法的仿真结果
3.2 动态障碍环境下的仿真验证
结合超车这一动态场景验证所提算法的有效性和可行性。APF算法的动态避障过程如图5所示。图5中,黑色填充区域是以恒定速度行驶的障碍物车辆,蓝色曲线代表智能车辆所规划的行驶路径。将传统APF算法与APF-Bug混合算法分别在该动态超车场景下进行验证。

(a) 换道过程 (b) 超车过程 (c) 并道过程 (d) 完整超车路径
图6为APF-Bug混合算法的动态避障过程,表2为传统APF算法与APF-Bug混合算法下的车辆位置信息。图5a和图6a为车辆行驶过程中的换道过程,对比发现,APF-Bug混合算法对障碍物的反应力更强,安全性能有明显提升。图5b和图6b为车辆超车过程,经过对比可以发现,APF-Bug混合算法相较于传统APF算法规划路径更加光滑,鲁棒性更强。图5c和图6c为车辆行驶过程中的并道过程,可以发现,APF-Bug混合算法并道时候离动态障碍物较远,可有效保证车辆行驶的安全性。图5d和图6d为车辆的完整超车路径,通过对比可以明显看出:传统APF算法不稳定,所规划的行驶路径距离障碍物较近,安全性没有保障,在实际应用中容易与障碍物发生碰撞;APF-Bug混合算法在动态障碍物场景下所规划的路径更加平滑,且在运动过程中与障碍物的距离较远,与传统APF算法相比,其安全性与稳定性都得到有效的提升。

(a) 换道过程 (b) 超车过程 (c) 并道过程 (d) 完整超车路径

表2 不同算法的车辆位置信息
4 试验验证
本章对自动避障系统的软件及硬件进行设计,搭建智能车试验平台。其中,智能车的软件部分主要以STM32系列单片机为控制核心,利用C代码将APF-Bug算法嵌入到芯片中,应用于超车场景,验证改进算法的有效性。智能车的硬件部分包括超声测距模块、电源系统、运动电机驱动模块等,主要通过产生脉冲宽度调制(pulse width modulation,PWM)脉冲控制智能车的转向和速度。其中,超声测距模块用于测量智能车在超车过程中与障碍车辆之间的距离,运动电机驱动模块用来驱动智能车的电机运转。自动避障系统的硬件组成框架如图7所示。
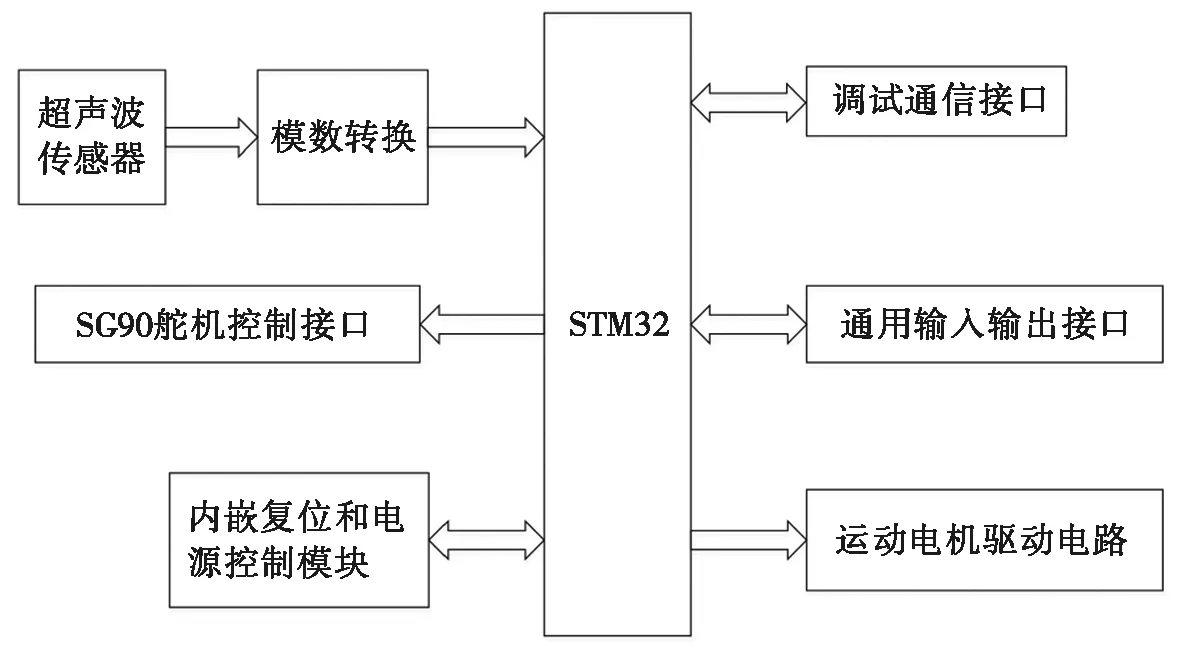
图7 自动避障系统的硬件组成框架
智能车的长度为245 mm,宽度为160 mm,前方障碍物车辆的长度为210 mm,宽度为185 mm,以智能车的尺寸大小为依据,设置车道线的宽度为260 mm,两车初始状态的位置如图8a和图9a所示。智能车辆通过超声波模块检测与前方障碍物车辆的距离,满足超车条件时,调整PWM波,使车辆向左转行驶到超车车道上并沿着车道中心线(白线)前进,两车位置如图8b和图9b所示。当智能车辆超过前方车辆时,两车的状态位置信息如图8c和图9c所示,智能检测与被超车辆之间的安全距离,在安全距离内向右移动,回到原车道线上,两车的位置信息如图8d和图9d所示。在整个试验过程中,模拟智能车处于理想状态以确保车辆在行驶过程中的安全性。

(a) 车辆初始状态 (b) 车辆换道过程 (c) 车辆超车过程 (d) 车辆并道过程
对比图8和图9可以发现:传统APF算法所规划的路径安全性没有保障,所规划的行驶路径不稳定,实际应用时极易超车失败;而APF-Bug混合算法能够按照仿真运行结果完成超车,但是超车过程中,由于车身配重问题使车身偶尔不能完全摆正,少数情况下会出现超车失败的情况,经多次试验验证统计,超车成功率在95%以上。

(a) 车辆初始状态 (b) 车辆换道过程 (c) 车辆超车过程(d) 车辆并道过程
5 结束语
本文针对智能车辆在静态、动态行驶环境下的自动安全避障问题,采用APF算法作为基本框架引入车辆运动学参数以改进APF算法,并应用Bug探索机制,提出了APF-Bug混合算法。经过仿真验证分析,证明所提混合算法可有效避免智能车在避障过程中陷入路径局部极值,同时在较低计算复杂度的前提下提高了路径规划的稳定性和安全性,确保智能车辆在动态行驶环境下安全可靠避障。在下一步研究中,面向更为复杂的动态混合交通流行驶环境,如何设计一种更加安全、平稳、高效的避障与超车路径规划算法将是我们研究的重点。

