粒子群算法改进灰狼算法的机器人路径规划

梁景泉，周子程，刘秀燕

（青岛理工大学信息与控制工程学院，山东青岛 266525）

0 引言

近些年来，元启发式算法在路径规划问题中的应用越来越广泛，代表算法包括遗传算法、蚁群算法和粒子群优化算法（Particle Swarm Optimization，PSO）。国内学者对元启发式算法进行了大量研究，例如王润泽等［1］提出利用蚁群算法进行动态路径规划，但由于该算法自身的局限性，前期搜索过程较慢，后期也有可能陷入局部最优解；缪裕青等［2］提出利用模拟退火算法改进的PSO 优化任务卸载策略，充分利用空闲的车载单元计算能力，但在精度方面仍不够理想；赵睿等［3］提出利用改进遗传算法优化自动导引车集结路径，算法中加入了基于时间仓的调整策略，从而使收敛速度进一步加快，但存在易过早得出最优解的问题。目前国内外还存在很多改进的单一算法，如Tsai 等［4］提出的改进遗传算法、Lee 等［5］提出的改进粒子群算法、Zhang 等［6］提出的改进蚁群算法、王海泉等［7］提出的改进人工蜂群算法、张文辉等［8］提出的改进人工鱼群算法等，均可用于路径规划问题求解，但鲜有研究进行两种方法的联合改进。

灰狼优化算法（Grey Wolf Optimizer，GWO）是由Mirjalili 等［9］提出的元启发式算法，属于群体智能算法，模仿灰狼的捕猎策略和阶层领导。该算法相较于其他群体优化算法有诸多优势，例如更加灵活、更容易实现以及求解过程中不需要计算梯度等。虽然GWO 在众多领域都有着良好表现，但其具有后期收敛速度慢和全局寻优能力不够强的问题［10］。因此，以该算法为基础，构建更加高效可靠的路径规划算法成为很多学者的努力方向。例如，曹建秋等［11］通过A*算法进行头狼初始化以获取较优起点，从而加快算法最优解的出现；王永琦等［12］采用反向学习方法构建初始灰狼种群，以提高初始解的质量，并借助精英反向学习策略探索优秀解的反向解，从而提升算法整体效率；袁光辉［13］通过引入非线性惯性权重以及自适应交叉编译策略对GWO 进行改进，以提高算法的收敛精度和速度。

目前，GWO 算法在路径规划实际应用方面仍有许多不足之处，为提高该算法的全局寻优能力和收敛速度，本文引入PSO 的思想改进GWO 算法，使其具有更加优秀的收敛速度和全局寻优能力。

1 环境建模

机器人全局路径规划问题的描述为：对于一个给定的二维地形，存在着有限个障碍物，算法的任务就是找到一个令机器人能够从起点到终点且安全不触碰障碍物的路径，并保证该路径为全局最短路径［14］。常见的环境建模方法有很多，如点集拓扑法、可视图法和栅格法等，本文选用栅格法，其目标函数可表示为：

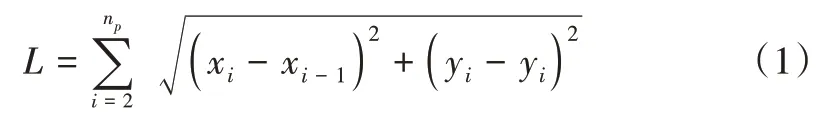
式中，L 为路径长度，np为路径点个数，（xi，yi）为对应路径点的坐标。

使用栅格法对机器人需要通过的环境进行建模后得到m×n 的区域，其中原点为机器人的初始位置，机器人最终要移动到的目标位置用（m，n）表示。如果障碍区域的形状不是规则正方形，那么将其补齐为正方形，建模时认定障碍物大小为整数个全栅格，若部分区域存在少量障碍，但障碍面积不满一个栅格，则将其看作一个栅格计算。

采用式（2）建立的栅格地图示例如图1 所示，有障碍物的栅格为黑色，表示机器人不能通过，不存在障碍物的栅格为白色，表示机器人能够通过。

Fig.1 Raster map model for path planning example图1 路径规划栅格地图模型图例

2 基础算法

2.1 GWO

GWO 是受灰狼的狩猎策略和社会等级启发得到的算法。灰狼分为4 个等级，即阿尔法狼（α）、贝塔狼（β）、德尔塔狼（δ）和欧米茄狼（Ω），见图2。领头或占优势的狼被称为α 狼，数量最少，主要负责为群体作出决策，如打猎时间等，它们并不一定是最强的成员，但却一定拥有最强的管理能力；狼群社会中第二等级的是β 狼，它们在许多活动或决策中协助α 狼，强化α 狼命令的执行，并向α 狼提供反馈；δ 狼服从α 狼和β 狼管理，但它们主宰着Ω 狼；Ω 狼是狼群中最低级的灰狼，它们总是屈从于其他类型的狼［9］。

Fig.2 Hierarchical structure of grey wolf population图2 灰狼群体等级结构

灰狼群体的狩猎策略是其另一个重要特点：狼群会在α 狼的领导下识别猎物位置并将其包围［15］。在灰狼的狩猎策略数学模型中，一般将最优秀的解决方案视为α，第二和第三最佳方案分别命名为β 和δ，其余命名为Ω。以下为灰狼捕猎机制的数学模型：

每次迭代后，新的灰狼组成员都会根据上一代α、β、δ狼（最优秀的三匹狼）更新位置，从而逐渐接近猎物，完成狩猎过程。

2.2 PSO

PSO 是Kennedy 和Eberhart［16］两位学者受到动物社会行为（如鸟类、鱼群的行为）启发提出的用于求解各类复杂优化问题的算法。该算法最初用于研究鸟类的觅食行为，但在实际应用中发现其优化能力强大，尤其在多维空间中表现突出。

该算法设计了一种理想粒子，鸟群中的每一个体都被抽象成这种粒子，每个粒子只具有位置和速度两种属性，每一个体都会单独搜寻最优解，并将其记为自身历史最优位置，而这个粒子的自身历史最优也会与整个群的其他粒子分享，全局最优解即为最优粒子的自身历史最优。粒子的适应度（与目标的距离）决定了其优劣，适应度的计算公式根据问题的不同而不同。

PSO 的初始态是一群随机分布的粒子，这些粒子各自会被初始化一个随机速度，经过不断迭代，最优解会逐渐产生。在迭代过程中，每个粒子都会根据其惯性、自身历史最优位置和全局最优位置进行位置更新，公式如下：

式中，V 表示速度；ω 为用于平衡全局与局部的惯性因子，数值一般为非负；r1、r2为分布在［0，1］范围内的随机变量；c1、c2为学习因子，一般为非负数；Pib表示对应粒子的历史最优位置；Pgb为全局最优位置。

值得一提的是，最初的PSO 很容易陷入局部最小，因此在算法中引入惯性权值ω，其值越高，粒子速度被保留得越好，能够更快搜索整个解的区间，因此具有更强的全局寻优能力，但也会使局部寻优能力更弱，更容易错过最优解，反之亦然。由于引入了ω，PSO 的适用性有了相当程度的提高，能应用于更多实际问题。

3 基于PSO改进的GWO

与大多数算法的改进方法不同，本文进行的改进不会使两种算法一个接一个单独进行计算，而是在运行过程中同时进行迭代进化，最终根据两个不同变量同时参与的结果生成问题的最终解决方案。因此，改进算法具有优化的PSO 局部寻优能力与GWO 全局寻优能力。

首先是GWO 的α 狼、β 狼和δ 狼（3 个最佳方案）迭代中的位置更新公式优化，具体见式（14）-式（16）。由式（10）、式（11）可知，GWO 的全局寻优与局部寻优能力主要由控制因子a 调节，某些情况下，由于搜索过程过于复杂，a无法有效平衡算法局部寻优与全局寻优的侧重。因此作为原方程式的替换，本文通过添加惯性权重ω控制GWO中全局寻优能力与局部寻优能力之间的平衡。

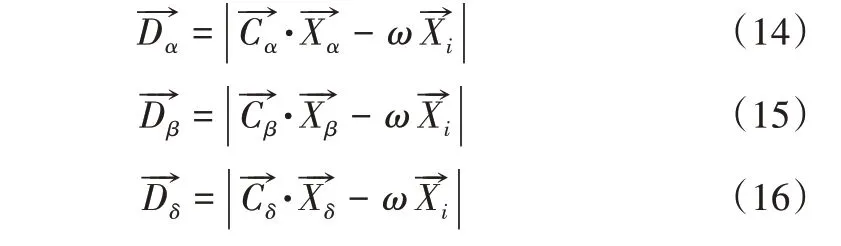
其次是将PSO 中的速度概念引入GWO 的位置和结果更新公式，具体见式（17）与式（18）。GWO 与PSO 不同，其在迭代过程中只考虑了α 狼、β 狼、δ 狼之间的关系与交流，忽略了自身经验的影响。而PSO 是善于利用粒子自身属性与信息的算法，因此在GWO 结果更新公式中融入PSO 的思想，能够得到性能更加优秀的改进算法。

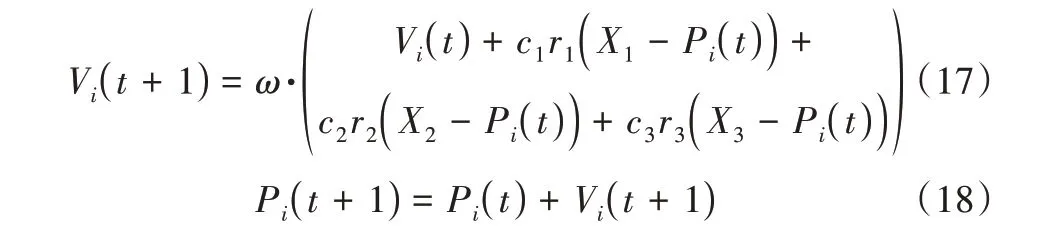
改进算法的具体流程如图3所示。

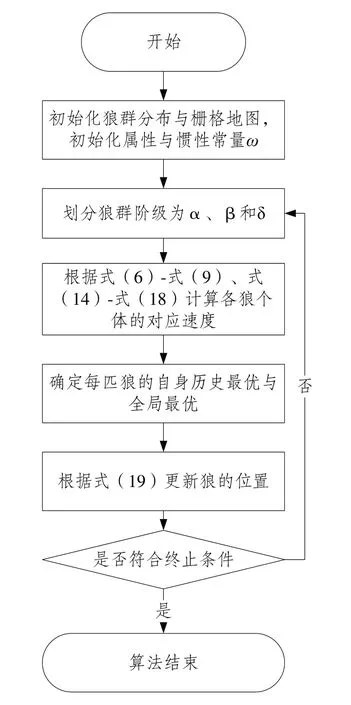
Fig.3 Flow of improved algorithm图3 改进算法流程

4 实验结果与分析

实验相关参数设置如表1 所示。其中，种群数量指计算过程中共有多少匹狼参与搜索过程；最大迭代次数指算法终止条件，当迭代次数达到最大时算法结束并输出最优解；ω指每匹狼的惯性因子，选取经多次实验后得到的较优数值；C1、C2、C3 为定义的3 个学习因子，在本次实验中与r1、r2、r3 相关，r1、r2、r3 均根据研究经验与实际验证取值为0.5。

Table 1 Parameter setting表1 参数设置

PSO 改进的GWO（PSO-GWO）与GWO 在实验样例测试中得到的结果比较如图4 所示。从图中可以看出，PSOGWO 的初始适应度值小于GWO，收敛速度比GWO 也有明显提高，最终得到的最优适应度值亦小于GWO，算法性能明显提升。

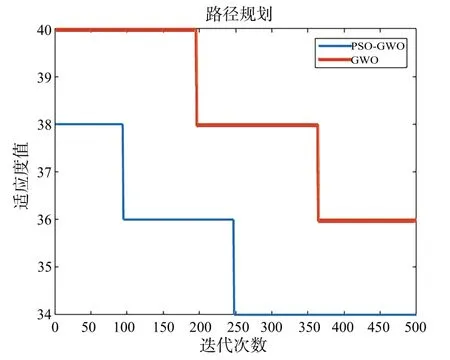
Fig.4 Comparison of results between（PSO-GWO）and GWO in experimental sample test图4 PSO-GWO与GWO在实验样例测试中的结果比较

PSO-GWO 与GWO 得到的路径图比较如图5 所示。可以看出，GWO 并未找到最优路径，存在部分多余路径，而经过改进后，PSO-GWO 能更加高效地对环境中的障碍进行分析，以更高的效率找到优于GWO 规划结果的更短路径。

为验证改进算法的性能，在栅格地图上随机生成障碍物进行5 次仿真测试，分别记录GWO 与PSO-GWO 的适应度与迭代次数。由表2 可知，PSO-GWO 比GWO 的适应度（路径长度）平均减少了4 个单位，迭代次数平均减少56次。综合分析可知，PSO-GWO 的性能更优、适应性更强，在大多数情况下都能获得比GWO 更优的规划路线。

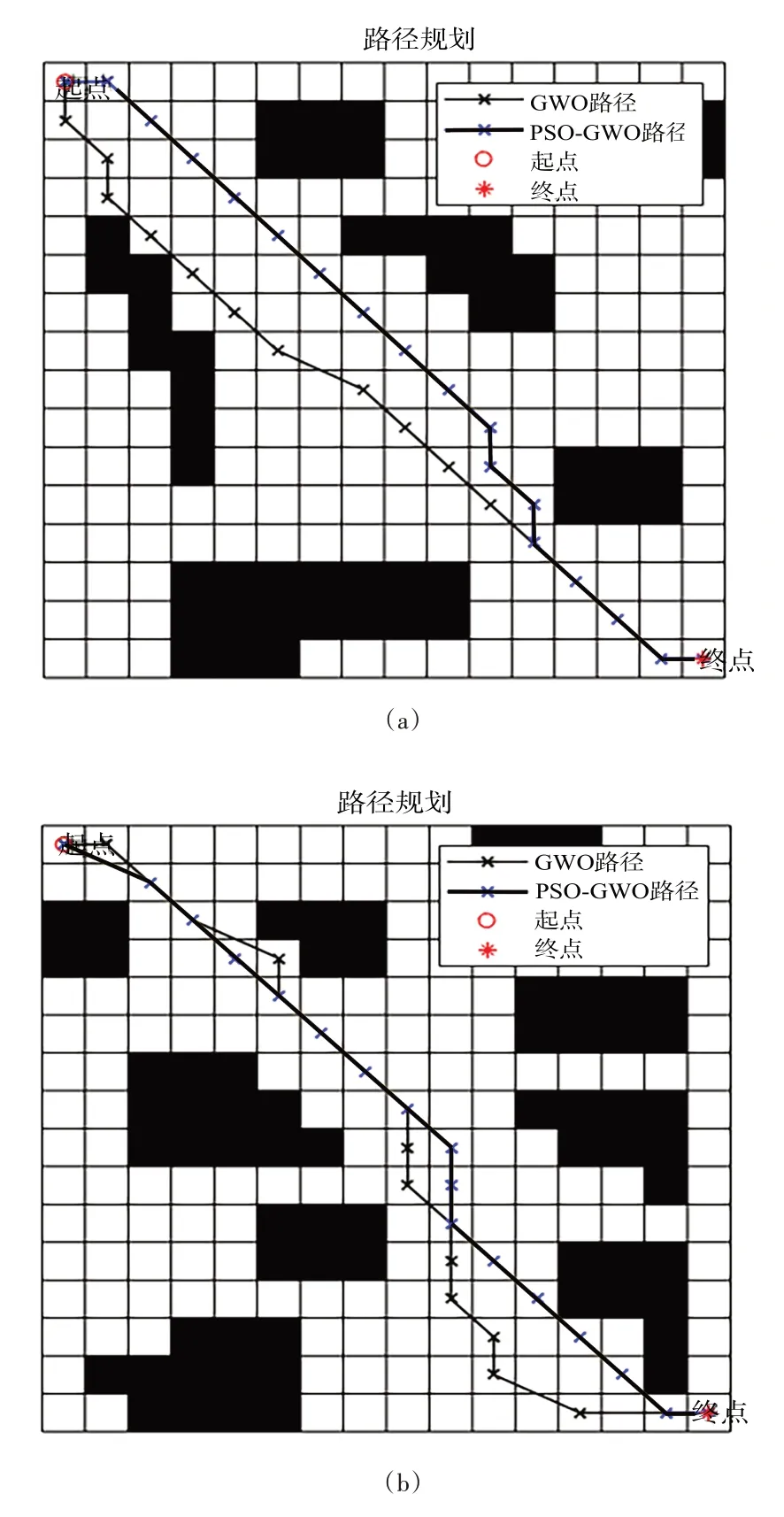
Fig.5 Comparison of optimization paths between PSO-GWO and GWO图5 PSO-GWO与GWO优化路径比较

Table 2 Performance comparison between PSO-GWO and GWO表2 PSO-GWO与GWO性能比较

5 结语

针对机器人路径规划问题，本文提出采用PSO 改进GWO，获得了比GWO 更优秀的性能，例如在大多数情况下能得到更好的初始适应度值，获得适应度最优解和搜索最优解所需的迭代次数更少，说明改进算法具有良好的时间效率和较强的适应性。然而，该算法尚未在复杂多变的实际环境中进行测试，后续会将该算法应用于实际环境中路径规划问题的求解，检验其实际可用性与抗干扰性。