基于遥感数据的不确定性的农业水资源优化配置研究——以漳河灌区为例

赵金淼 佟 玲* 岳 琼 郑 静 黄 鑫 李 鹏

(1. 中国农业大学 中国农业水问题研究中心，北京 100083；2. 湖北省漳河工程管理局，湖北 荆门 448156)

在全球经济快速发展和人口不断增长的背景下，持续增长的用水需求与有限水资源之间的矛盾日益突出。我国是农业大国，农业作为最大的用水主体，面临着前所未有的用水挑战。据我国水资源公报统计，我国2020年农业用水量为3 612.4 亿m3，占总用水量的62.1%，耕地实际灌溉亩均用水量356 m3；而我国人均水资源占有量仅为世界平均水平的1/4，农田灌溉水有效利用系数仅为0.565[1]。农业水资源供需不匹配、利用效率低及时空分布不均等问题严重制约了我国农业可持续发展。合理的用水策略可以节约35%的水和能源[2]。灌区是灌溉农业生产的重要载体[3]，探究灌区供需水空间分布，实行更科学有效的水资源分配与管理[4]，对提高水资源的利用效率、缓解水资源供需矛盾以及保障粮食生产安全具有重要意义。

农业水资源优化配置是结构复杂的大系统优化措施，具有多尺度、多层次、多阶段、多变量和非线性等特点[5]。在开展水资源优化配置，降雨量作为基本参数时，具有很强的时空变异性，增加了建模的难度。遥感技术的利用和地理信息系统的发展使获取更多空间信息成为可能[6-7]，充分利用遥感信息开展更精准的农业水资源空间分布研究是当前热点。

由于水资源配置过程中存在着管理、水文气象和作物价格等诸多不确定性因素，针对农业水资源优化配置系统中的不确定性问题，随机数学规划、区间参数规划和模糊数学规划等不确定性方法已被广泛应用于研究农业水资源优化配置系统中的不确定性[8]。农业水资源优化配置系统中的降雨量、水价和种植面积等系统参数可能更复杂，单一因素的不确定性方法很难量化其特征。例如，水价、惩罚系数等参数具有模糊特征，采用模糊数能够更好的表示其变化范围和中间趋势。然而在大多情况下，很难获得这些参数确定的模糊隶属度函数，而将带有上下边界的区间数引入到模糊隶属度函数中，构成模糊区间隶属度函数能够很好地解决水资源优化配置系统中的不确定性问题。张帆等[9]将这模糊区间隶属度函数的模糊区间集引入到灌溉水分配模型，用来处理水资源优化配置模型中的双重不确定性参数。在实际灌溉中，优化目标和约束条件作为水资源优化配置系统中基础构件，往往需要考虑存在于优化目标和约束条件双侧的模糊区间参数。同时，风险是由水资源优化配置系统的不确定性因素引起的，水资源系统的不确定性因素必然带来水资源优化管理的风险，需要开发反映系统不确定性和风险规避的灌溉水资源优化模型[10]。国内外目前对水资源优化的理论研究已经取得了较多的成果，如潘琦等[3]结合渠系输水模拟和土壤水量平衡模拟构建的渠系优化配水模型，为灌区水资源管理提供指导；赵敏等[11]结合Jensen模型与土壤水平衡模型实现灌区尺度灌溉水资源优化配置；岳琼[12]等构建区间两阶段模糊可信性约束规划模型,实现灌区各用水户间水资源优化配置。已有研究中的水资源优化配置系统中的降雨参数多采用以点带面的形式，忽略降雨量的时空变异性进行水资源优化配置，结合遥感数据进行灌区水资源优化的应用研究较少。位于湖北省的漳河灌区降雨量年内分配不均匀，年际分配也不均匀，丰枯不均匀，当漳河灌区降雨不足时，需要灌溉以满足作物生长的用水需求。因为漳河灌区曾旱情频发，2010年秋至2014年连续5年干旱，且旱情通常伴随着降雨强度小、时空分布不均的特点[13]，导致供需矛盾突出，因此有必要结合遥感降雨数据，针对典型枯水年进行水资源优化。

本研究以漳河灌区作为研究区域，基于灌区遥感降雨量数据，引入模糊可信性约束规划，以同时处理系统不确定性参数和违规风险，构建全模糊区间可信性约束非线性规划模型，得到更精细的优化管理方案，为管理者提供丰富的决策参考，助力农业水资源高效利用与精准管理。研究内容主要包括：(1)探究遥感和雨量站降雨量数据结合方式，获取漳河灌区典型年降雨空间分布情况；(2)引入水分生产函数定量表征各时段作物产量对水分亏缺的响应；(3)引入区间数和模糊区间数分别处理模型中的单一不确定性和双重不确定性；(4)引入模糊可信性约束规划权衡系统效益和约束违反风险；(5)开发相应的算法，求解优化模型，生成高效的农业水资源分配方案。

1 研究区概况与基础数据

1.1 研究区概况

漳河灌区位于我国长江流域,湖北省中部，流域范围介于东经111°～112°，北纬30°～32°，由副坝、一干渠、二干渠、三干渠、四干渠、西干渠和总干渠等7个分灌区组成(图1)，流域面积2 980 km2。漳河灌区内有漳河水库，漳河水库是由观音寺、林家港、王家湾和鸡公尖4座水库通过3段明渠串联而成。其中观音寺水库在最前端，有来水多库容小的特点，鸡公尖水库在最末端，有来水少库容大的特点。水库来水情况较为复杂，从多个支流来水，出水口也不唯一。漳河水库周围公路较多，交通便利，漳河水库服务着漳河灌区260多万亩农田。

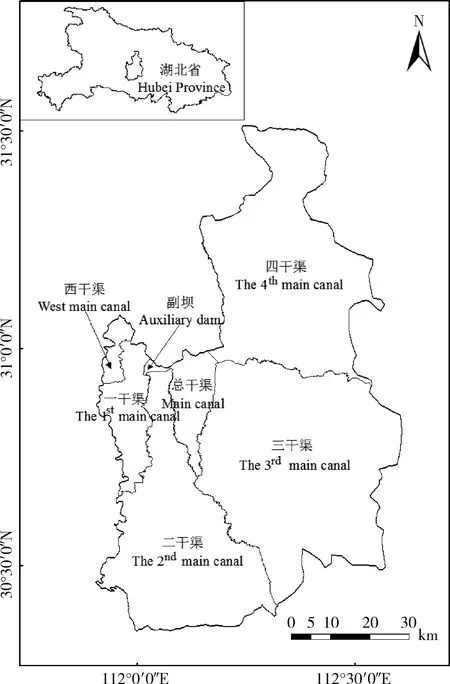
图1 湖北省漳河灌区位置图Fig.1 Location map of Zhanghe irrigation area,Hubei Province

漳河灌区西北偏高东南偏低，海拔高程自-4～461 m，高程空间变异性较大，属于亚热带大陆性气候。年蒸发量700～1 000 mm，月最大150 mm，月最小16.5 mm[12]。漳河水库多年平均年降雨量969.7 mm，降雨量年内分配不均匀，年际分配也不均匀，丰枯不均匀[12]。降雨多集中在4月至9月，约占全年的70至80%。水库径流量还有连续多年丰、枯变化显著的现象。漳河灌区的主要农作物是水稻、冬油菜和冬小麦。因为降雨和地下水完全可以满足冬季油菜或冬小麦用水需求，所以水稻是主要灌溉作物。

2 模型的构建

2.1 空间降雨ULRR模型

2.1.1遥感数据集预处理

MODIS是美国NASA对地观测系统系列遥感卫星平台上的主要传感器，具有36个光谱通道，每1～2 d可以获取一次全球地表数据，其波段范围广，数据更新频率快。使用投影变换、裁剪、重新采样[14]和空间建模来处理2014—2020年5—8月GPM数据，然后在WGS-1984坐标系中删除无效值，以获得空间分辨率为0.1°的漳河灌区空间遥感降雨数据集。

降雨作为农业水资源管理的重要参数，具有很强的时空变异性。为进一步校正降雨数据集的准确性，本研究以2014—2020年5—8月盐池、安栈口、温家巷、车桥、掇刀、周集、张场、三界和四方等雨量站点生成了288个采样序列，并收集采样序列的降雨量和上述时段研究区域内的GPM面数据。采用ArcGIS软件中的多值提取到点工具获取采样序列GPM点值，并对采样序列的降雨量和GPM点值进行变化趋势分析。

2.1.2线性回归

采用一元线性回归(ULR)方法缩小空间数据，具体方程如下:

Y=a0+a1X

(1)

式中：Y为雨量站站点降雨标准化值；X为雨量站站点GPM的标准化值；a0、a1为回归系数。每个网格的回归结果可以通过以下函数得到：

Yj=a0+a1Xj

(2)

式中：Yj为第j个网格的ULR结果值；Xj为第j个网格上GPM的月标准化值。

2.1.3反距离权重

采用GIS软件计算ULR方法所得值与地面气象站观测结果之间的残差,将残差进行反距离权重插值,计算公式如下：

(3)

式中：Rj为第j个网格残差值；Zi为第i个雨量站站点残差值；n为雨量站站数；di为第j个网格到第i个雨量站的距离；p为距离影响因子。

2.1.4降尺度空间降雨数据集结果

各网格的最终降雨情况计算公式如下：

Pj=Yj+Rj

(4)

式中：Pj为第j个网格的降雨量结果；Yj为第j个网格的ULR结果值；Rj为第j个网格的残差值。

2.1.5交叉验证

分别采用GPM数据、一元线性回归方法(ULR)、反距离权重方法(IDW)和线性回归残差方法(ULRR)获取漳河灌区降水量空间分布情况，采用交叉验证方法[15]与ULRR方法进行比较，评估ULRR方法的适用性。使用均方根误差(RMSE)、平均绝对误差(MAE)和平均相对误差(MRE)作为评估不同方法的标准。这些指标的计算公式如下：

(5)

(6)

(7)

式中：Pi为第i个估计结果；Mi为第i个观测结果；n为雨量站站点数。

2.1.6水分敏感指数处理

为了量化灌水量在不同时期对产量的影响，进而量化关键生育期需水权重，需要建立以各生育期供水充足程度与产量比的关系。其中用得比较多且较适合我国水稻生育规律的最普遍的形式有4种[16]，此处采用Jensen模型水分生产函数，模型结构是连乘形式。根据张帆[9,17]研究，Jensen模型各生育阶段的水分敏感指数时间尺度与其他时间尺度可以通过累加原则互相转换，可以将水分敏感指数的时间尺度统一到月尺度。

模型具体表达形式如下：

(8)

式中：j为6、7、8和9月编号；Ya为作物的实际产量，kg/hm2；Ym为最大产量，kg/hm2；ETcj为第j月的实际作物需水量,mm；Wij为第i个网格j月的实际灌水量,mm；Pij为第i个网格j月的有效降雨量，mm；bj为第j月的水分敏感指数。

基于Jensen模型和相关文献[18-19]，Jensen模型各生育阶段的水分敏感指数时间尺度与月尺度可采用下式计算：

(9)

式中：bj为第j月水分敏感指数；dt为第t个生育期包含天数；λt为第t生育期水分敏感指数；dj为j月内月内包含天数；D为生育期内每个月的天数。

2.2 基于遥感数据的不确定性农业水资源优化配置

2.2.1目标函数

为了准确反映不同生育期作物对水分的需求，最大化经济效益，本研究建立基于作物水分生产函数的灌水量分配优化模型。据张祖莲等人的研究[17]，Jensen模型在描述湖北省水稻生长方面被认为优于其他水分生产函数。为了更好地解决不确定的问题，根据漳河灌区的特点，本研究引入了一种基于期望值的(EVB)[18]方法来处理在模型目标和双重约束中,以梯形模糊区间集表示的种植面积和可用供水参数；采用95%置信区间数表示作物价格、作物产量和种植面积等参数；此外，本研究希望反映与违反系统约束相关的复杂性，所以对可供水量参数采用可信性约束。因此，建立模糊区间可信性约束非线性规划模型，解决漳河灌区灌溉用水管理中的灌水量问题：

(10)

式中：F为经济效益，元；i为各个分灌区(i=1,2,…,7)，包含副坝、一干渠、二干渠、三干渠、四干渠、西干渠和总干渠七个分灌区；j为主要生长月份，包含5、6、7和8月；BY表示作物价格，元/kg；Ym为充分灌溉条件下作物最大产量，kg/m2；Ai为i分灌区的种植面积，m2；Wij为i分灌区j月灌水量，是决策变量，mm；Pij为i分灌区j月降雨量，mm；ETcj为j月实际作物需水量，mm；bj为j月水分敏感指数；C为种植成本，元/m2。

2.2.2约束

模型目标受到以下约束：

1)可供水量限制。

(11)

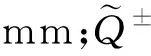
2)作物需水量限制。

(12)

(13)

式中：Wij为i分灌区j月灌水量，是决策变量，mm；Pij为i分灌区j月降雨量，mm；ε为最低需水系数，通过漳河灌区调研数据获得；ETcj为j月实际作物需水量，mm。

3)非负性约束条件。

Wij±≥0, ∀i,∀j

(14)

2.2.3模型求解方法

步骤1：建立模糊区间可信性约束非线性规划模型。

步骤2：将目标函数和约束条件中的模糊数转化为其期望值。例如ξ的期望值被定义为[19]：

(15)

(16)

步骤4:一般来说，为了避免违反约束条件的高风险，显著的可信度水平应大于0.5。基于步骤3，模糊区间可信性约束非线性规划模型可以转换为典型的区间模型，如下：

(17)

约束：

(18)

(19)

(20)

Wij±≥0, ∀i,∀j

(21)

步骤5：通过交互算法将区间模型分解为两个子模型[21-22]。由于目标函数是求最大化的利益，因此应首先求解上界子模型。

步骤6：求解上界子模型，并在不同给定的可信度水平下得到相应的方案。

步骤7：根据步骤6得到的解，求解对应的下界子模型，得到相应的解。

步骤8：结合步骤6和步骤7中的解决方案，在给定的每个可信度水平下生成最终灌水量分配方案。

2.3 基础数据

本研究对1964—2019年降雨量进行频率分析，选择频率为80%的2014年为典型枯水年进行研究。本研究所使用的遥感数据来自于全球降雨测量(Global Precipitation Measurement)数据，2014年4月1日发布，空间分辨率为0.1°，时间分辨率为月。气象数据从中国气象数据服务中心(http:∥data.cma.cn/en)下载。通过调研和文献[13,24]收集2003年到2018年度社会经济资料、作物种植面积、作物产量和水文资料，如表1。通过调研获取2014—2020年间包括盐池、安栈口、温家巷、车桥、掇刀、周集、张场、三界、四方、藤店等雨量站降雨量数据。通过调研获取漳河灌区最大作物产量为11 500 kg/hm2，平均种植费用为7 000元/hm2。

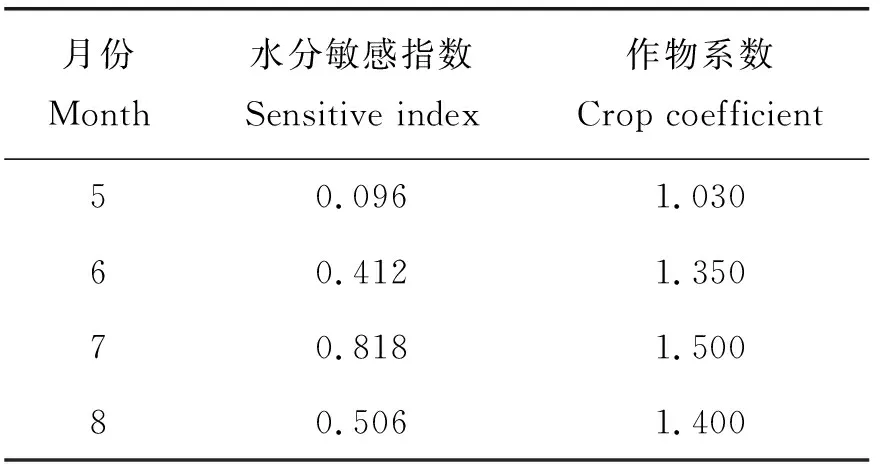
表1 漳河灌区基础参数Table 1 Basic parameters of Zhanghe irrigation area

漳河灌区水稻各个生育期内不同月的实际作物需水量(ETc)采用作物系数法[23]确定。其中，根据灌区团林气象站1988—2018近30年间气象数据，采用Penman-Monteith公式计算得到1988—2018年5—8月参考作物需水量(ET0)[24],如表2。水稻生育期各月的作物系数通过参考文献[13]和[23]和实地调研获取，计算公式如下：

ETC=KC×ET0

(22)

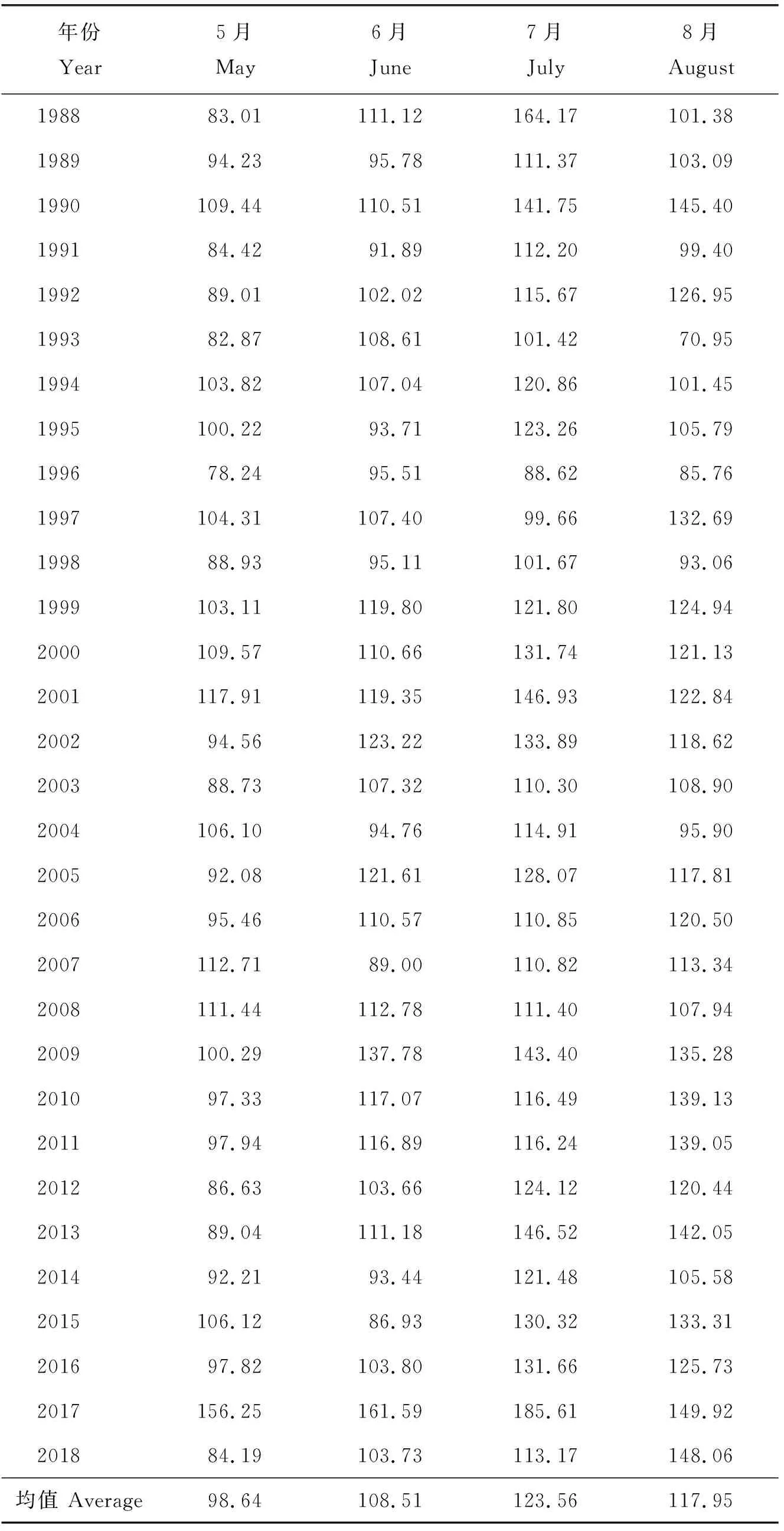
表2 1988—2018年5—8月参考作物需水量(ET0)情况Table 2 Reference crop water requirement (ET0) from May to August, 1988-2018 mm

式中：ETC为实际作物需水量计算值，mm；KC为作物系数；ET0为参考作物需水量，mm。

3 结果与分析

3.1 遥感GPM数据与降雨量的相关性

图2显示随着采样序列的变化，GPM值和雨量站降雨量变化趋势相似，但是GPM值明显高于雨量站站点降雨量，这表明GPM值存在一定的高估问题。通过趋势图可以明显看出，GPM遥感数据与雨量站点降雨数据集有着明显的趋势一致性，所以可以采用线性回归方法分析。

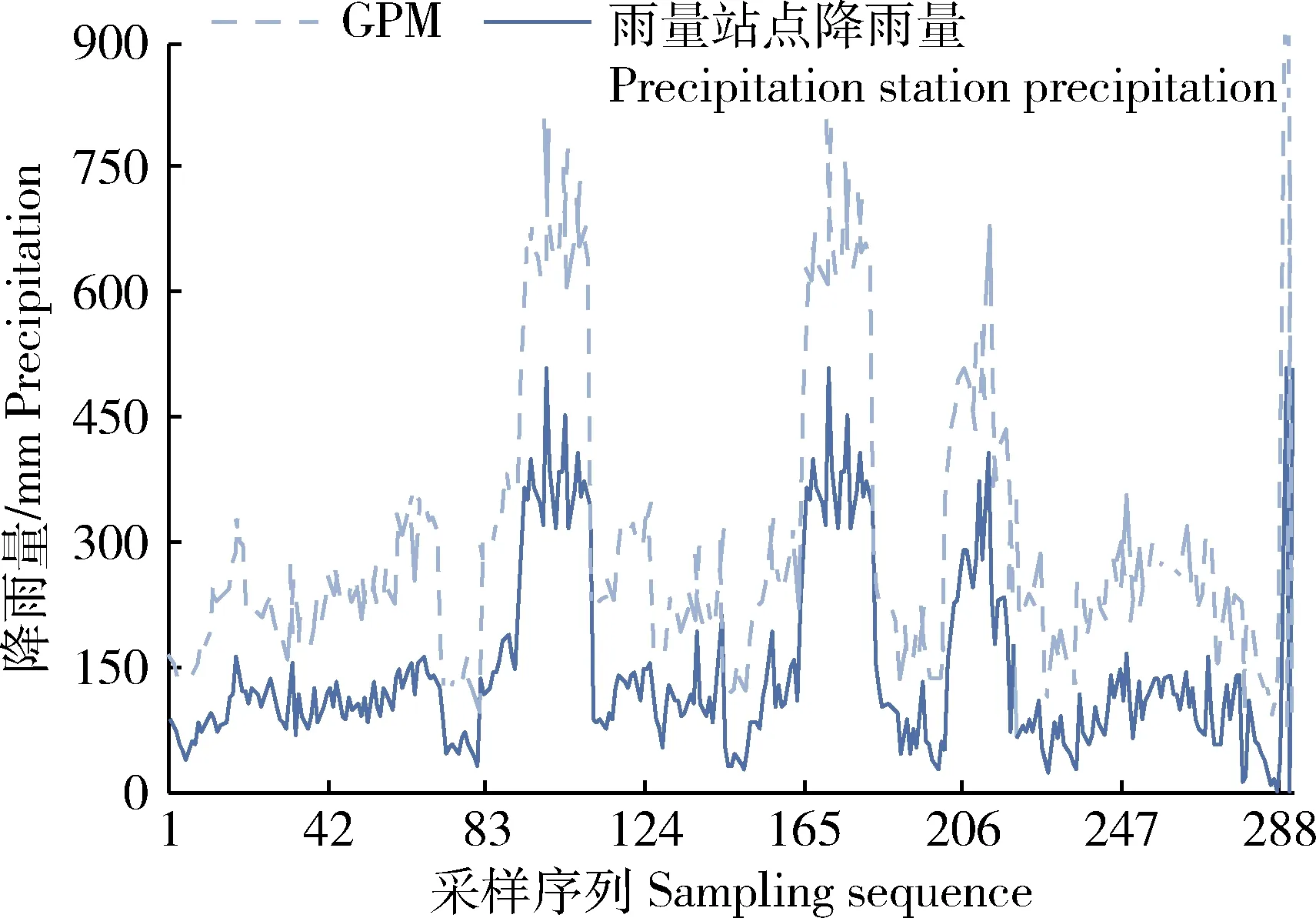
图2 GPM值与雨量站降雨量变化情况Fig.2 Variation of GPM value and precipitation at precipitation station

3.2 空间降雨数据集

通过前面趋势图可以明显看出，GPM遥感数据与雨量站点降雨数据集有着明显的趋势一致性，传统水资源优化配置中使用的降雨量数据集都是基于以点带面的形式，未考虑各个分灌区的空间变异性，为进一步提升降雨数据集的准确性，本研究采用一元线性回归方法，通过2.1.1的方法计算，可以得到回归方程如下：

Yj=0.046+0.714Xj

(23)

式中：Yj是第j个网格的ULR结果值；Xj表示第j个网格上GPM的月标准化值。

利用漳河灌区全流域多个雨量站点2014年5—8月各月的降雨数据，利用公式23，在ArcGIS中进行空间线性回归，得到全流域的各月降雨的空间线性回归结果。通过采用2.1.1的方法，首先将线性回归结果与雨量站降雨数据进行对比，然后对残差采用IDW方法进行插值，最后使用按掩膜提取工具，用漳河灌区各个分灌区边界图提取各个分灌区的降雨结果，得到2014年漳河灌区各个分灌区5—8月降雨的空间分布,见图3。如图所示随着月份的变化，各个灌溉分区的降雨量具有明显的变化，而且即使在同一月，各个分灌区的降雨量也有明显的空间变异性。

由于降雨受地形、气象等多种因素的影响，降雨量在估算过程中存在不确定性。区间参数能较好地描述空间插值过程对降雨量的不确定性。将降雨空间分布结果图中各个分灌区降雨量的最大和最小值>乘以有效降雨系数，从而得到有效降雨量的上下界。图3显示四干渠的降雨量变异性最为显著，降雨量最高最低值差异较大，说明该区域空间变异性较大，而且不同月份降雨量差异性也较大，时间变异性也较为明显。而副坝、一干渠、西干渠降雨量差异性不明显，说明这些灌溉分区的降雨情况相对稳定。

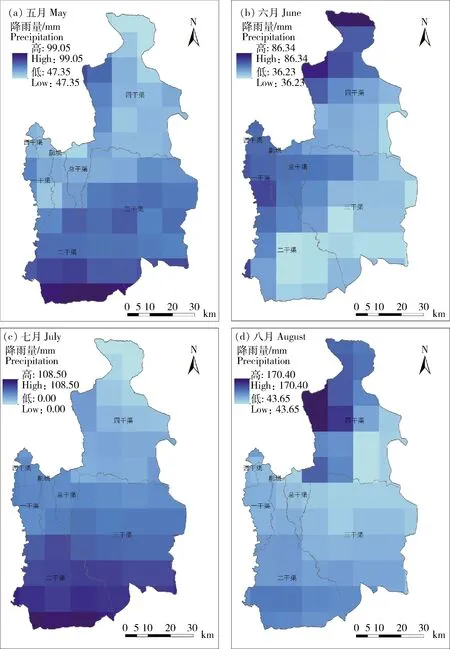
图3 2014年漳河灌区各个分灌区 5—8月降雨的空间分布Fig.3 Spatial distribution of precipitation in each sub-irrigated area of Zhanghe irrigation area from May to August in 2014

随后将交叉验证方法[9]用于与GPM数据，线性回归(ULR)，IDW方法和ULRR进行比较来衡量ULRR方法的适用性。其中，均方根误差(RMSE)，平均绝对误差(MAE)和平均相对误差(MRE)是用于评估不同方法准确性的重要指标。可以计算每个方法的3个指标，RMSE、MAE和MRE，结果见表3。在这些方法中，ULRR方法的性能最好，表明ULRR方法可以提高预测结果的精度。

表3 GPM, ULR, IDW, ULRR方法的平均绝对误差，平均相对误差，均方根误差测算结果Table 3 Test results of mean absolute error, mean relative error, root mean square error by using GPM, ULR, IDW and ULRR methods

3.3 不同可信度水平下最佳灌水量配置

表4为漳河灌区在可信度水平为0.8情况下不同分灌区5、6、7和8月的最优农业灌水量分配。可知：灌溉与降雨可以很好地满足二干渠、四干渠、西干渠各个月的作物用水需求，5月相较于其他阶段需水量满足程度较低，这与5月的作物缺水敏感性较低的预期相一致。5月缺水程度最低的是二干渠和三干渠；6月二干渠和三干渠缺水程度显著增高，这是由于降雨量随着月份的变化，空间变异性较大的原因，分配到不同分灌区和不同月份的灌水量随着降雨量的减少而增加。

表5为可信度水平为1时，各个分灌区5、6、7和8月中最佳农业灌水量分配。由于分灌区之间的不同月份降雨量变异性显著，表5显示各分灌区的最佳灌水量不相同，其中，副坝和四干渠的需水程度最大，一干渠、西干渠、总干渠次之。表5中显示了作物主要生育期中5—8月的最佳分配水量，结果表明，当无法充分满足5、6、7和8月需水量时，供水优先考虑6、7月，其次是8月，这个结果与作物的缺水敏感性、需水量和降雨有关，具体来说，总体5月的降雨可以满足作物需水量，但随着作物的生长，6、7和8月作物需水量显著增加，而且这个时期的作物水分敏感性较大，而6月相对于7月作物需水量较低，容易被满足，所以显示6月满足程度最高，而7月需水量满足程度第二。根据表4和表5进行比对，随着可信度水平的增加，对于6、7和8月的最佳灌水量无显著影响，主要是提高了5月的配水量，这与前面5月缺水敏感性较低的预期一致。

表4和表5比较可以看出，随着可信度水平的上升，8月最佳农业灌水量有一定程度的上升，这与8月敏感指数较大相一致；并且随着可信度的上升，5月最佳农业灌水量也有一定程度上升，这可能是5月需水量满足程度较低，所以可信度水平上升时，5月需水量满足程度上升。随着可信度水平的上升，系统的安全性和可靠性增强，系统的风险降低，这可以为灌区管理者提供参考[11]。

由表4和表5可知，尽管8月的四干渠和总干渠需水量最大，但分配水量较少，这与降雨量直接相关。降雨对灌水量分配影响较大，5月各个分灌区的最佳灌水量从南向西北依次递增，6月最佳灌水量呈现从东南到西北依次递减的趋势。还可以看出，7和8月对缺水更加敏感。这两个关键增长阶段的缺水造成的生产损失很难通过其他增长阶段的更多灌溉来弥补。因此，应优先考虑7和8月的灌水。因此，可提出以下几点建议：1)考虑各个分灌区配水量的空间优先性，5月优先考虑副坝、总干渠、一干渠的配水，6月优先考虑二干渠和三干渠的配水，7月优先考虑四干渠、西干渠、副坝、一干渠的配水，8月优先考虑二干渠、三干渠、一干渠、副坝的配水；2)7月必须满足作物需水量；3)模糊区间可信性约束非线性规划模型得到的最优方案提供更好的选择，保证灌溉供应不足时系统的效益。此外，最优农业灌水量分配结果有助于产生合理的灌水量分配，并减少枯水年降雨时空变异性大造成的缺水量。

表4 可信度水平为0.8时的最佳灌水量上下限Table 4 Upper and lower limits of optimal irrigation amount under the reliability level 0.8 mm

表5 可信度水平为1时的最佳灌水量上下限Table 5 The upper and lower limits of optimal irrigation amount when the reliability level is 1 mm

3.4 净系统效益

通过模糊区间可信性约束非线性规划模型来分配各个分灌区的灌水量，从而获得系统净效益。在不同的可信度水平下，解决方案和相应的经济效益也不同。由于输入参数的不确定性，我们将解作为区间值给出，当可信度水平达到1时，系统效益达到[7.89×1010，2.61×1011]元，当可信度水平达到0.8 时，系统效益达到[7.88×1010，2.60×1011]元，可以发现随着可信度降低，净系统收益也有一定程度的降低。较高的可信度水平对应于模型结果的约束满意度和较高的可信度水平，可信度水平可以被视为优化结果的可靠性的一个指标。灌水量是发展当地农业经济的重要因素，实际上，应该更加注重降水量的时空变异性，从而对灌水量的在时间和空间上进行更好的统筹规划；可信度水平越高，经济效益越高，但对应的灌溉水资源总量也有所提升，灌区管理者应结合实际情况，选择相应可信度水平下的方案，从而提高水资源利用率。

4 结 论

本研究构建了基于遥感数据的不确定性农业水资源优化配置模型，并将其应用于漳河灌区，得到了2种可信度水平下的最佳灌水方案。主要结论如下：1)ULRR方法预测结果的精度最高；2)漳河灌区各个分灌区的降雨量具有明显的时空变异特征；3)在降雨情况和作物需水量情况相同的背景下，可信度水平越高，系统净经济效益越大；4)由于5月的缺水敏感性较低，而且缺水程度普遍较低，灌水量相对较少，在分配水量时，优先考虑7、8月的配水；5)此外，当可信度水平为1时，达到[7.89×1010，2.61×1011]元净经济效益，当可信度水平达到0.8时，系统效益达到[7.88×1010，2.60×1011]元。本研究验证了模型在灌区尺度结合遥感数据进行单一粮食作物水资源优化配置的可行性，将为类似地区解决有限水资源配置问题提供配置思路与模型基础。在实际的区域农业水资源配置中变异性较大的数据还有很多，因此在未来的研究中，可考虑基于本研究模型框架，构建结合多种空间参数的优化配水模型，来指导实际水资源配置。