NEPE推进剂初始模量与平衡模量关系研究①
王小英,钱 勖,薛元利,汪 越,张峰涛
(1.航天化学动力技术重点实验室,襄阳 441003;2.湖北航天化学技术研究所,襄阳 441003;3.陕西电器研究所,西安 710025)
0 引言
固体推进剂在长期贮存中,由于热应力及药柱自重产生的载荷(持久载荷)将伴随发动机装药整个寿命周期,因此发动机对推进剂的持久承载能力提出了较高的要求。固体推进剂的持久承载能力考察主要包括长期定应力、长期定应变作用下推进剂的破坏情形,及在长期载荷作用下模量变化,并将长期载荷下的平衡模量作为固体火箭发动机装药结构完整性分析的重要参数进行分析。
平衡模量的获取方法主要分为定载法(试验周期3个月)和定应变松弛模量主曲线法。定载法是将推进剂试样在一定载荷下存放3个月后的模量作为平衡模量。国内在松弛模量获取方法上研究较多,其测试是基于恒定变应作用、在不同温度下测试模量并绘制成松弛模量主曲线,对主曲线进行拟合得到平衡模量值。可见,平衡模量测试方法均存在试验周期长,实验量大,无法大量测试的问题。而固体推进剂的单向拉伸初始模量测试速度快,可大批量测试。因此,研究推进剂单向拉伸的初始模量与平衡模量的关系,从而根据初始模量值快速预估平衡模量值,具有较强的实用价值。
平衡模量作为发动机设计的重要参数,但该数据无法及时获取,发动机设计人员只能按照一定的比例关系,由推进剂常温初始模量推算出平衡模量,并将常温初始模量作为常规的测试指标要求。但在实际研究过程中发现,部分推进剂的初始模量值明显低于技术指标要求,但发动机工作正常,表明推进剂的力学指标明显偏高。因此,关于初始模量与平衡模量两者的关系需专门开展研究。经调研,目前仅有部分相关文献。国内池旭辉等利用弹性模量一凝胶分数关系模型,预测得到了化学参量表征老化效应的衬层应力松弛模型,但未提出能否应用于固体推进剂。FRANCIS等研究了TP-H1011 推进剂松弛模量与应变率的关系,结论为应变老化仅使短期内的松弛模量降低,但随时间延长,应变老化推进剂松弛模量与零应变老化推进剂模量逐渐重合。以上文献均未直接指出推进剂的初始模量与平衡模量的关系。
本文针对NEPE高能固体推进剂,重点研究了常温初始模量及初始模量主曲线与松弛模量主曲线的关系,为快速获取平衡模量提供一条途径,也为今后固体推进剂模量调节指导方向。
1 试验
1.1 试验材料及方法
试验所用材料为NEPE高能固体推进剂,其固体填充颗粒(HMX、AP和AL)质量分数为74%,粘合剂(PEG/NG/BTTN)及小组分质量分数为26%。
根据QJ 924—1985标准,将NEPE推进剂制成标准哑铃型试样。应力松弛试验参照QJ 2487—1993执行,采用Instron 4502材料试验机测试。单向拉伸主曲线测试参照GJB 770B—2005《火药试验方法》执行。
1.2 基本概念
(1)初始模量:又称弹性模量或杨氏模量。表示材料拉伸曲线起始弹性阶段直线部分的斜率,用来描述材料在外力作用下变形难易程度的指标。在材料拉伸初始阶段,应力与应变成正比例关系,其比例系数即是弹性模量或初始模量。初始模量一般作为材料拉伸结构能力的表征,主要反映材料抵抗应变的能力。对于某些材料例如粘弹性的推进剂在初始弹性范围内应力应变曲线不符合直线关系的,可根据需要取切线弹性模量、一定应变范围内的割线模量等人为定义的方法作为初始模量值。
推进剂初始模量的测试标准有QJ 1812—1989与GJB 770B—2005-方法413.2,两种标准均定义初始模量为应力应变曲线中初始直线段部分的斜率。直线段可以取3%~7%割线部分,也可取5%割线部分或其他明显直线段(图1)。国外直接采用初始线性比例部分(切线)的应力应变之比作为初始模量(图2)。当应力应变曲线初始段接近线性时,几种方法测试结果基本相当;反之,差异较大。
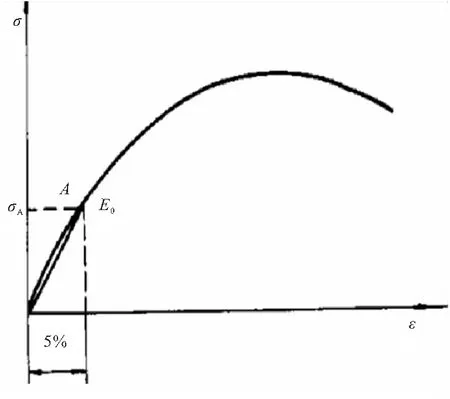
图1 拉伸应力-应变曲线上正割值
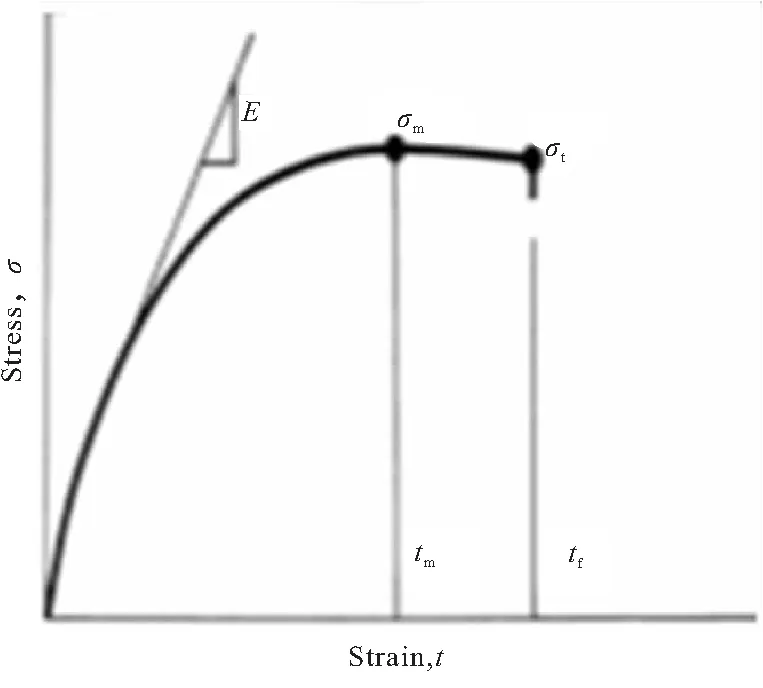
图2 推进剂初始模量
材料试验机Instron 4502中Instron Bluehill数据软件可计算两种标准方法推荐的3%~7%及5%割线模量作为初始模量外,还给出1%~3%割线模量和自动模量作为初始模量值。
具体计算公式为式(1)或式(2):

(1)
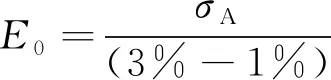
(2)
5%的割线模量值受挂样松紧状态影响较大,取值跨度宽、且受制于应力应变曲线零点,因此实际使用较少。自动模量是指将拉伸曲线中最大抗拉强度之前应力应变曲线按照应变等分为6个区域,对6区域分段拟合所得的线性关系式的最大斜率,其单个计算区域应变范围为/6,取值跨度过宽,自动模量不宜作为NEPE推进剂的初始模量。
由于NEPE推进剂1%~3%阶段较3%~7%更符合初始模量定义,也更接近标准规定的初始直线段,割线取值跨度适中,且受松垂校正影响较小,实际测试中常选该段值作为初始模量。本文以1%~3%时的割线模量作为初始模量。
(2)应力松弛模量:指在线性粘弹性材料的应力与恒定伸长率的比值。国内一般采用QJ 2487—1993规定的方法采用单轴试样开展试验,将单轴试件承受恒定的伸长率下测试应力随时间变化过程,两者比值即是应力松弛模量表示为
()=()
(3)
式中()为时刻的应力;为试验规定的恒定伸长率。
平衡模量是指应力松弛足够长的时间后,应力()不随时间变化时的松弛模量,此时松弛模量基本保持恒定,故称为平衡模量。
实验测试时,首先测定不同温度下的应力松弛模量,绘制成松弛模量主曲线(图3),对主曲线采用普朗尼级数表示为
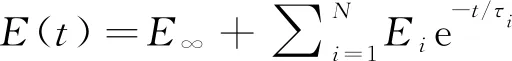
(4)

图3 应力松弛模量主曲线
式中为材料的平衡模量,表示时间为无穷大时的模量,代表可恢复的弹性模量。
国外在测试推进剂应力松弛模量主曲线时,为消除应力集中,常采用末端粘结过的单轴试样或圆柱形样本开展应力松弛试验,具体见图4。本文采取QJ 2487—1993方法执行。应力松弛模量一般作为火箭发动机的缓慢冷却时和恒定温度下贮存时所承受的力学载荷参数输入。
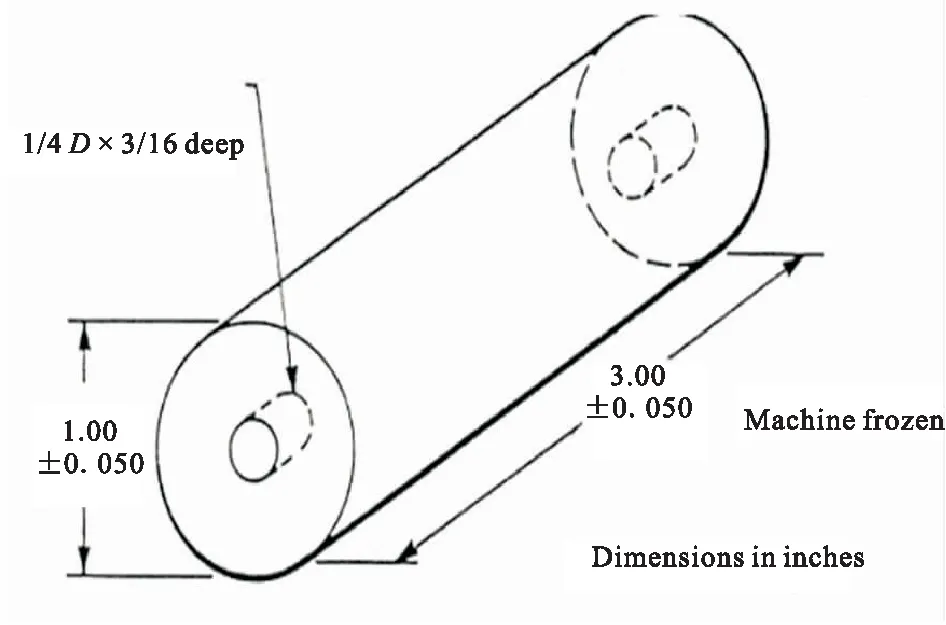
图4 应力松弛圆柱体试验样本
几种不同模量用途及测试难易程度差异性见表1。
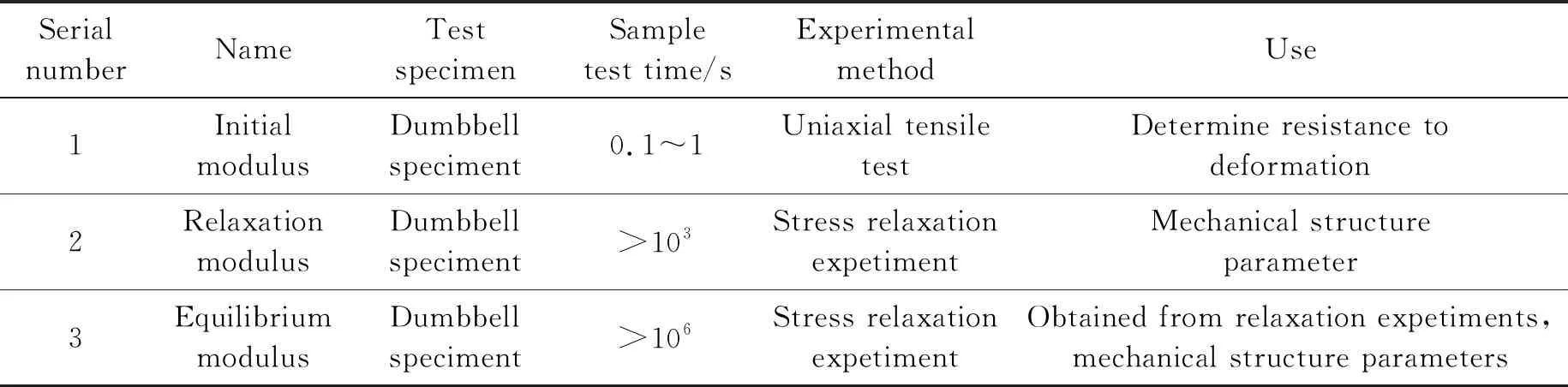
表1 三种模量的主要差异性
因此,研究推进剂单向拉伸的初始模量与平衡模量的关系,从而根据初始模量值快速预估平衡模量值,具有较强的工程应用价值。
2 试验结果与讨论
2.1 NEPE推进剂松弛模量主曲线
参照QJ 2487—1993标准给出了某批次高能推进剂(其常温初始模量==1.60 MPa),该批次推进剂应力松弛模量主曲线测试结果见图5。
NEPE高能固体推进剂属于颗粒填充交联聚合物材料,其松弛特性主要由粘合剂基体决定。根据交联聚合物松弛特性,当处于较低温度时(链段松弛时间>>观测时间),粘合剂基体的链段运动困难,此时处于玻璃态,松弛模量主要为普弹模量。当升至较高温度(<<),链段可自由移动,聚合物处于高弹态,瞬时响应模量随温度升高而变小,随时间进一步延长,松弛模量趋于稳定。
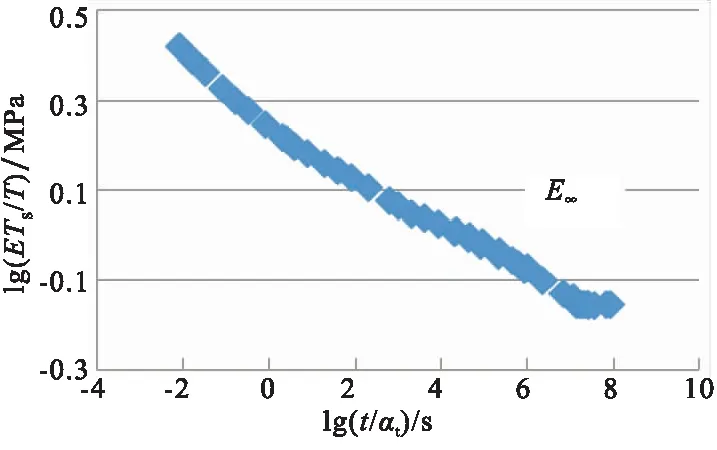
图5 某高能推进剂配方的应力松弛模量主曲线
由图5可知, NEPE推进剂松弛模量主曲线随时间变化规律与交联高聚物基本一致。随时间延长逐步降低,当时间lg()≥6.9 s后,松弛模量变化很小,此时推进剂模量已趋向稳定。基于此,工程中取100 d时(相当于lg()=6.93 s)的松弛模量等效为推进剂平衡模量,或者采用Prony级数拟合松弛模量主曲线计算出平衡模量。为便于计算,本文以100 d时间对应的模量视为平衡模量值。
测试了不同NEPE高能推进剂配方常温25 ℃下初始模量值及平衡模量值,结果见图6。
由图6可见,随NEPE推进剂常温初始模量的增加,推进剂的平衡模量呈现增加趋势,但线性关系较弱,线性相关系数仅有0.70。
固体推进剂的初始模量及松弛模量均是在小变形(5%应变附近)状态下测得的参量。NEPE推进剂一定温度下初始模量表达式为
=(1+)
(5)
式中为粘合剂基体的交联密度;为填料增强系数;为填料密度;为填料比表面积;Ф为填料体积分数。
式(5)表明,一定温度下,固体推进剂的初始弹性模量主要由粘合剂基体交联密度确定,与固体填料颗粒增强作用相关。
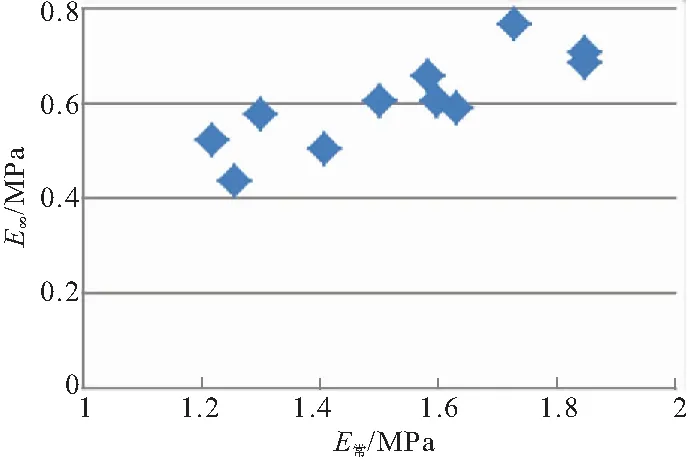
图6 初始模量(25 ℃)与平衡模量的关系
池旭辉在其论文中指出,交联聚合物的平衡模量大小主要由聚合物的交联密度决定。推进剂初始模量和平衡模量都与其交联密度密切相关。
固体推进剂的交联密度包含物理和化学交联密度。在常温初始模量测试时,采用哑铃试样进行拉伸,加载方式是恒定拉伸速率(=100 mm/min),换算成时间尺度为0.1~1 s(样品伸长/拉速),测试时间短,高分子链基本无松弛过程。此时推进剂的初始模量由物理和化学交联密度决定。在应力松弛试验中,松弛模量加载方式是恒定应变,试验测试时间尺度在10~10s之间。由于作用时间长,高分子链缠结在应变过程中逐步释放,物理交联随时间延长逐渐减弱,后期在松弛模量趋于平稳时仅化学交联存在。
以上分析表明,时间尺度差异性导致固体推进剂的初始模量与平衡模量有部分决定因素相同,但也存在一定差异性,直接用常温初始模量预测平衡模量误差较大。
2.2 NEPE推进剂初始模量主曲线与松弛模量主曲线
根据以上分析,常温初始模量与松弛平衡模量主要在测试时间尺度上差异较大。利用时温等效原理,将初始模量也绘制成与时间相关的主曲线(此时拉伸应变速率的量纲转化为s),实现应力松弛加载时间与应变速率的转换与统一,以观察相同时间尺度下初始模量与松弛模量的关系。结果见图7。
由图7可见,在相同时间区域内,初始模量主曲线和松弛模量主曲线基本平行。将初始模量-折合时间双对数主曲线左移1.2个单位,可与松弛模量主曲线重叠。即初始模量加载时间与恒应变折合时间的关系为
lg()=lg(1)-12
(6)
折合时间相差Δlg()=1.2 s。针对不同的固体推进剂,折合时间差值可能不同。
根据图7,表明在相同时域下,可用极慢拉下的初始模量预示平衡模量。为验证以上结论,重现选取了另一组常温初始模量较高的NEPE高能推进剂3配方(常温初始模量为2.43 MPa),同时测试松弛模量主曲线及初始模量主曲线(折合时间左移1.2)进行对比,结果见图8。

图7 NEPE推进剂初始模量主曲线与松弛模量主曲线
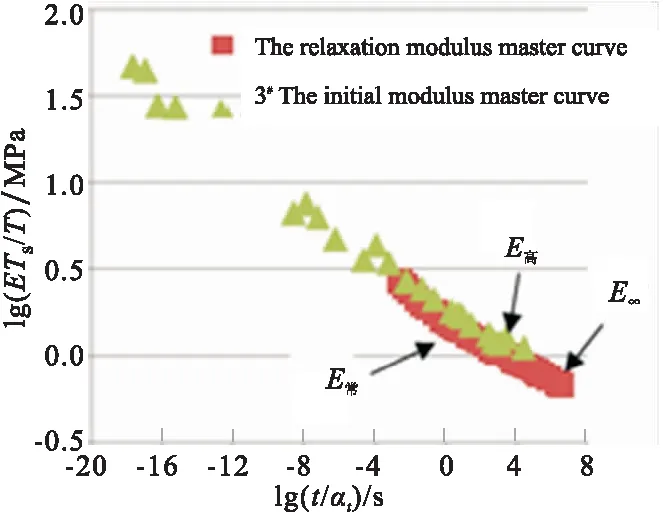
图8 松弛模量主曲线及初始模量主曲线关系
由图8可见,在相同时域区间,初始模量主曲线和松弛模量主曲线基本重合。试验结果与图7结论一致。图8中,NEPE推进剂在高温慢拉下(工程常用70 ℃、2 mm/min拉速测试,折合时间lg()=3.32 s),推进剂的物理交联也逐步减弱,此时初始模量相比常温初始模量(折合时间lg()=-0.155 s)更接近于松弛平衡模量。因此,可建立高温初始模量与平衡模量关系,见图9。
图9中,70 ℃下推进剂的初始模量与平衡模量具有较好的线性关系,线性相关系数=0.90。对比图6和图9,表明利用高温下推进剂的初始模量可更精确的预测其平衡模量。因此,后续推进剂力学性能测试中应重点关注高温下推进剂的初始模量值,也可通过对比高温下推进剂初始模量的差异对配方进行优化调节,以获得满足平衡模量指标要求的推进剂配方。
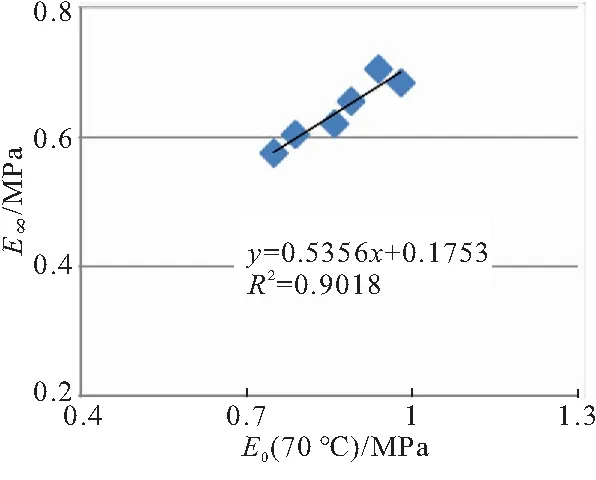
图9 初始模量(70 ℃)与平衡模量关系
3 结论
(1)当加载时间与应变速率统一后,NEPE推进剂的初始模量主曲线几乎与松弛模量主曲线重合,表明不同测试方法下模量具有一致性。
(2)NEPE推进剂在高温70 ℃慢拉下的模量相比常温初始模量更接近于松弛平衡模量,且高温下推进剂的初始模量与平衡模量具有较好的线性关系,可利用高温极慢拉下的初始模量预估平衡模量。

