基于Ansys-Workbench EPKM点火过程流固耦合仿真分析①
刘迎宾,李 卓,江晓瑞
(内蒙古工业大学 理学院,呼和浩特 010051)
0 引言
固体火箭发动机的点火过程具有持续时间短、升压梯度大的特点。点火过程中,药柱内表面容易产生升压不均匀的现象,导致药柱结构完整性发生破坏,这属于发动机内流场与固体推进剂相互作用的流固耦合问题。
关于固体火箭发动机流固耦合问题的研究始于1991年,美国PQM-1固体火箭助推器在地面静态试验时点火阶段发生爆炸,CHANG等通过流固耦合仿真计算,对爆炸原因进行了分析,为其改进提供了可靠依据。近年来,国外一些学者在流固耦合计算模型及数值方法方面做了研究,如JOHNSTON等采用一种特殊的时间迭代技术将流场求解器、结构场求解器进行耦合,用于分析运载火箭的推力振荡现象,TOLA等将内弹道流场与结构场相互耦合分析,对槽形药柱的结构进行优化。国内关于固体火箭发动机点火过程流固耦合的研究起步较晚。2000年,国防科技大学张为华等利用N-S方程,新型的ENO差分格式进行数值计算,定性研究了点火药喷流与主装药形状的相互影响,提出固体火箭发动机装药设计中应该注意的问题。之后,周红梅、曹琪等指出了对固体火箭发动机点火过程流固耦合研究的重要性,并利用MPCCI软件作为流场与结构场数据的交换平台,分别对含有裂纹装药及带有径向翼槽大长径比装药的固体火箭发动机点火过程进行了仿真分析。黄永恒利用流固单向耦合方法对管形及星形装药发动机点火过程中药柱的受力情况及影响因素进行分析。近年来,一些学者通过冷流冲击试验来模拟发动机药柱在点火过程中受高压燃气的冲击作用,利用流固耦合分析方法,对药柱结构场在冲击过程中的变化规律进行研究。
通过对前人工作的学习与总结,发现有关固体火箭发动机点火过程流固耦合的研究成果相对较少,而且由于计算机软硬件的限制,前人大多只能做一些相对简单的计算,却需要大而繁琐的工作。近年来,随着Ansys商用软件的发展,其Workbench可以通过调用其内部的各个模块,进行耦合分析。本文通过Workbench调用Fluent及Mechanical APDL模块分别用于对发动机流场及结构场的计算,并通过调用System Coupling模块对其进行耦合分析,以EPKM型固体火箭发动机为算例,研究了其点火升压阶段燃烧室内流场及结构场的变化规律,为固体火箭发动机的设计及故障诊断提供参考。
1 仿真计算模型
1.1 几何模型
EPKM型固体火箭发动机用于将载荷从近地点轨道推进到地球同步转移轨道,其主装药头部含有12个沿周向均匀分布的翼槽。为了节约计算资源,只对从翼槽的中间对称面,绕发动机轴线旋转15°的区域进行建模,模型尺寸见表1。由于在点火计算过程中,固体推进剂点燃后,需要利用Fluent的源项法,通过UDF(User-defined function)从靠近药柱内表面的一薄层流场区域内加入高温燃气,故在建模过程中,需对该区域进行单独建模,即图1中Source area。采用四面体非结构化网格对模型进行网格划分,如图1所示。

表1 EPKM模型尺寸

图1 EPKM几何模型及其网格划分
1.2 控制方程
燃气流动与传热的连续方程,动量方程,能量方程可用共同的形式表达,使用通用变量,通用微分方程为
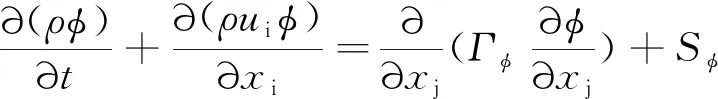
(1)
式中 第一项为瞬变项或时间项;第二项为对流项;第三项为扩散项;为对应于变量的扩散系数;末项为源项。
结构场单元基本平衡代数方程为
[]{}=[]{ü}+{}+{}
(2)
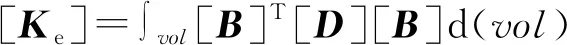
1.3 计算模型
湍流模型选用Spalart-Allmaras单方程模型,其输运方程:
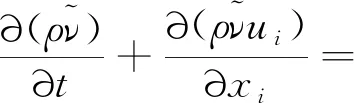
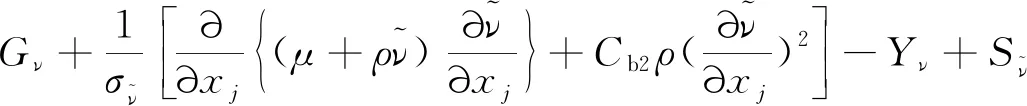
(3)
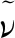
固体推进剂的燃速模型:
=1044×100278
(4)
式中为燃烧室压强。
温度为3300 K的燃气在相应流率下所具有的焓可用下式计算:
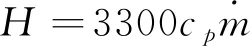
(5)
式中为燃气的比定压热容,J/(kg·K)。
固体推进剂为粘弹性材料,其体积松弛模量用1~9参数的Prony级数给定:
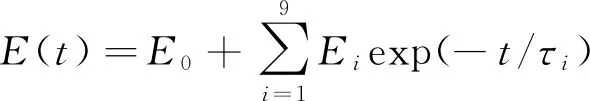
(6)
其中,各参数如表2所示,其瞬时弹性模量(=0)=18.87 MPa,泊松比为0.498,密度1750 kg/m。
EPKM的点火装置为点火发动机,采用HTPB系统配方推进剂药柱,计算中假设点火装置产生的燃气与主装药产生的燃气具有相同物理性质,如表3所示。

表2 Prony级数参数

表3 燃气的物理性质
1.4 流固耦合方法
文中采用的流固耦合方法包括两种,如图2所示。其中,图2(a)表示流固双向耦合,主要通过System coupling对耦合迭代的时间步长及流场与结构场对应面上压力与变形量数据的传递进行控制。图2(b)表示一种简化的流固单向耦合方法,其计算过程是先完成流场部分的计算,再将不同时刻流场对结构场的压力直接传递到结构场进行受力分析,该方法不需要在每个时间步进行数据的双向传递。因此,计算速度相对于第一种会非常快,但只能计算流场流动状态基本不受结构场变形影响的情况,且只能是某些间断时间点处结构场的状态。
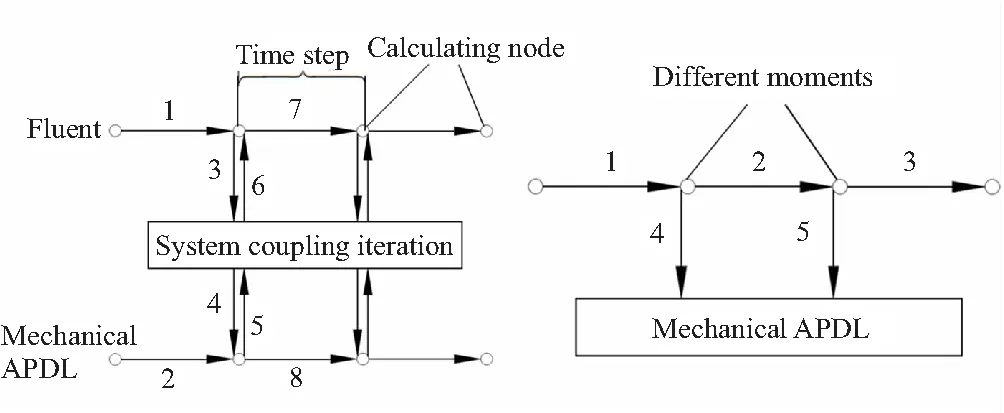
(a)Bidirectional coupling (b)Unidirectional and simplified coupling
1.5 初始和边界条件
仿真计算中流场区域入口位置如图3所示,将其设置为质量流率入口,流率按图示曲线变化,为保证主装药的稳定燃烧,点火发动机在整个点火过程一直处于工作状态。流场区域出口,即喷管出口截面设置为压强出口,大气背压约1000 Pa,温度约1200 K。堵盖打开前,将堵盖处边界设置为Wall,堵盖打开后,将其改为Interface,堵盖的打开压强为2.5 MPa。流场模型的侧面设置为Symmetry对称边界。初始状态,燃烧室内整个流场速度为零,压强和温度为在地面对燃烧室进行密封时的压强和温度,即1 atm和300 K。

图3 点火燃气入口位置及其流量曲线
将药柱内表面与流场外表面都设置为流固耦合面,并在流场中设置移动边界。计算过程中,将流场的压力数据传递到结构场,将结构场产生的变形量数据传递到流场。将药柱的剩余面都设置为光滑面约束。
只有在高温燃气流经药面时,药面才会被加热引燃。因此,用药柱内表面附近流体单元的温度和压强来判断药柱是否被点燃。通过对Fluent进行编程嵌入,计算过程中获取药面附近流体单元的温度和压强并进行判断,当其同时达到一定值时,认为该单元附近药柱被点燃。然后,从该单元处往流场中加入3300 K的高温燃气。流率由燃速决定:
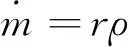
(7)
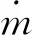
计算过程中忽略侵蚀燃烧对推进剂燃速的影响。由于点火过程所用时间极短,因此忽略药柱燃面的径向位移。不考虑药柱由于固化降温引起的温度载荷,只对点火升压过程中的内压载荷进行计算。
1.6 网格无关性验证
为分别对流场和结构场网格进行无关性验证,先增加流场网格数,计算0.1 ms时发动机头部某点处压强,再增加结构场网格数,计算药柱在该时刻的最大应力,如表4所示。

表4 不同网格数计算结果
随着网格数增加,流场某点压强变化最大约 0.75%,结构场最大应力变化最大约0.26%。网格数的增加对计算结果影响很小。最终采用流场网格数230 392,结构场网格数26 246。
2 仿真结果分析
药柱在初始几个毫秒内,由于点火燃气的冲击作用,会产生相对较大的变形,因此采用图2(a)所示流固双向耦合计算方法对点火过程计算5 ms,药柱最大变形量随时间变化曲线如图4所示。可以发现,其最大变形量不到1 mm,对流场的影响基本可以忽略。因此,为了加快计算速度,假设在整个点火过程中药柱的变形量很小,基本不会对流场产生影响,采用图2(b)所示简化的流固单向耦合方法完成后续的计算,并根据燃烧室压强达到稳定工作压强时药柱的最大变形量大小对假设进行验证。
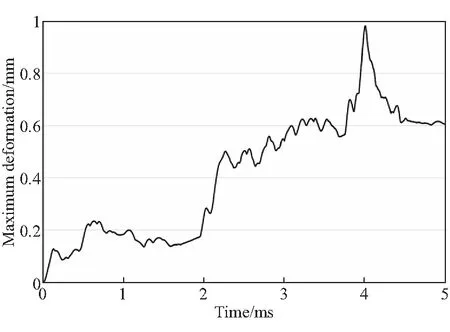
图4 结构场最大变形量随时间变化曲线
2.1 燃烧室内流场分析
主装药点燃前,燃烧室内燃气完全来源于点火发动机。由图5可知,点火燃气由点火发动机喷出后,首先不会直接流过药柱的头部内表面,而是先从燃烧室轴线附近流动到其尾部,经堵盖作用,再回流到头部翼槽区域。在翼槽内的流动情况如图5中=26 ms、=34 ms和=57 ms所示,先流动到翼槽的前缘,然后沿着前缘逐渐向其底部和后缘流动,最后填充满整个翼槽区域,而且发动机燃烧室内初始时刻的冷空气会被点火燃气压缩到翼槽内,使该区域的温度相对较低,药柱的点燃延时相对较长。
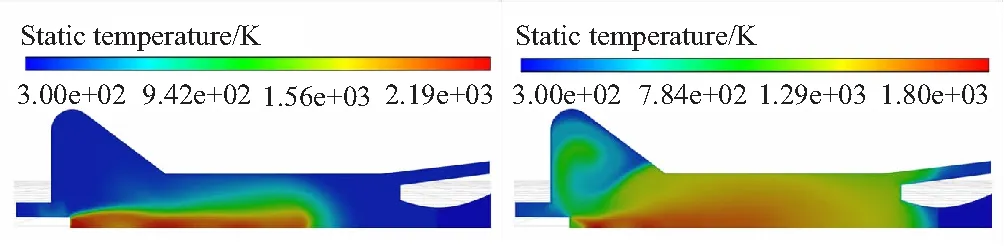
(a)t=10 ms (b)t=26 ms
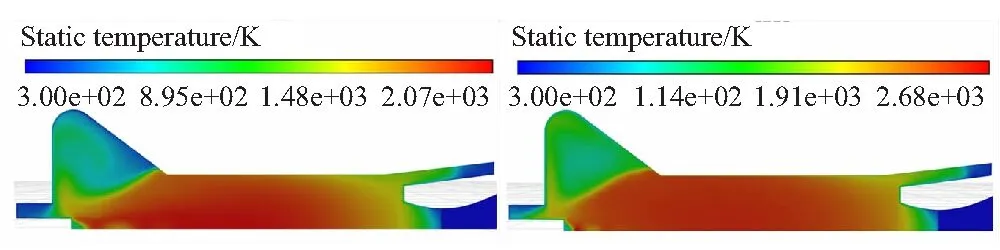
(c)t=34 ms (d)t=57 ms
点火燃气刚喷入燃烧室后会形成复杂的多个涡流,其后它们会逐渐进行融合并变得稳定,见图6。在=12 ms时,管型药柱段内的流场已基本变得稳定,只存在一个相对较大的涡流,在=18 ms时,翼槽内流场也变得稳定,到=22 ms时,整个燃烧室流场基本达到稳定的状态。此时,燃烧室管型药柱段和翼槽内各存在一个相对较大且稳定的涡流,直到堵盖打开,该流动状态基本不会再发生变化。
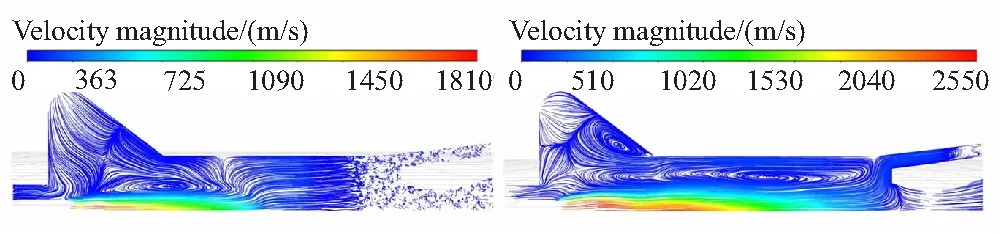
(a)t=2.5 ms (b)t=12ms
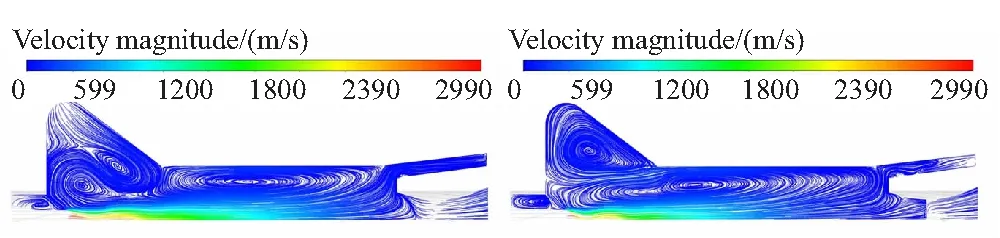
(c)t=18 ms (d)t=22 ms
对比图7中=57 ms和=57.8 ms时刻主装药内表面沿轴向温度分布曲线,显然在=57.8 ms时,在距燃烧室头部约0.6 m处温度突然升高,即在=57.8 ms时,主装药已经被点燃,而且由图8可知,首先被点燃的位置位于翼槽到管型药柱段的过渡区域。

(a)t=57 ms
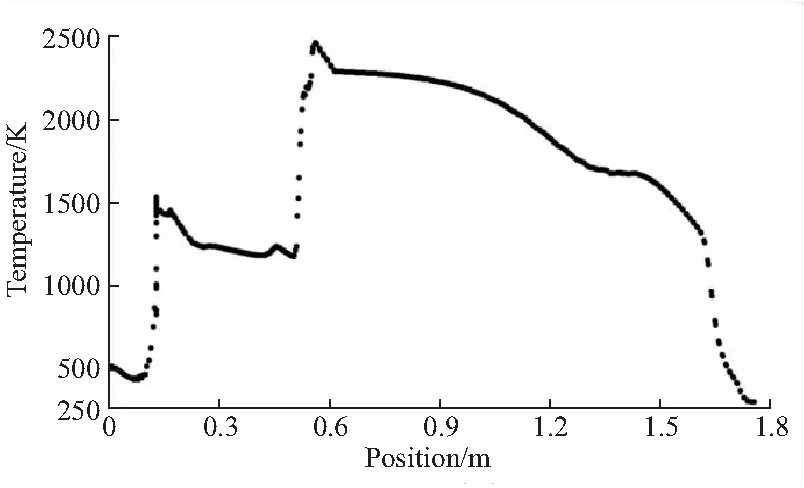
(b)t=57.8 ms
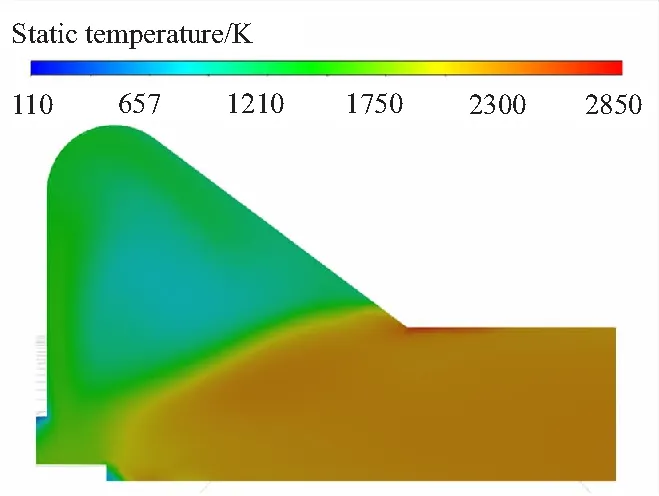
图8 t=57.8 ms时翼槽附近温度云图
主装药点燃后,燃面从首先被点燃处分别向头尾两端扩展,且在管型药柱段的扩展速度远大于向翼槽内的扩展速度,如图9所示。其原因如前所述,翼槽内含有大量压缩的初始时刻燃烧室内冷空气,相对温度较低。燃面在翼槽内的扩展过程为:首先,在翼槽到管型药柱段的过渡区被点燃,燃面以非常慢的速度向翼槽内扩展,大量推进剂燃气会随着从燃烧室尾部回流的点火燃气向翼槽的前缘流动,前缘被点燃;然后,燃面逐渐向翼槽底部和后缘方向扩展。
当燃烧室堵盖面平均压强达到2.5 MPa(约67 ms时),堵盖打开,燃烧室内涡流逐渐消失,如图10所示。最终主装药产生的高温燃气直接流向喷管,由喷管喷出,不再产生涡流,燃烧室内达到新的稳定流动状态。
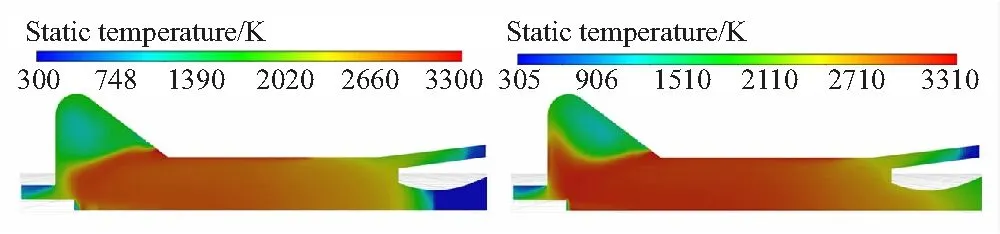
(a)t=64 ms (b)t=68 ms
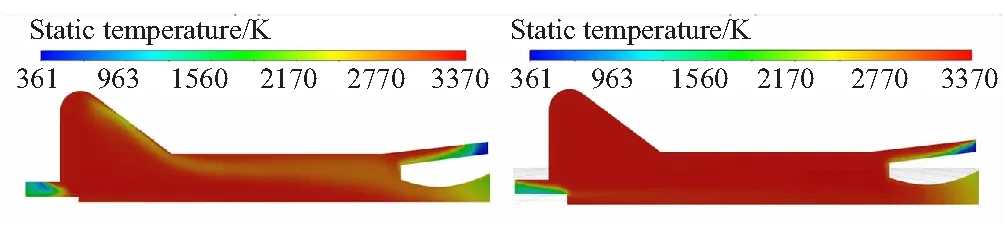
(c)t=90 ms (d)t=117 ms

(a)t=67.5 ms (b)t=69 ms

(c)t=72.5 ms (d)t=80 ms
2.2 药柱结构场分析
点火初期,发动机燃烧室堵盖打开前,由图11中的=13 ms和=64 ms时刻药柱变形量云图可知,药柱尾部的变形大于其头部,原因是由于喷管堵盖的作用,使得燃烧室内流场尾部的压强始终大于其头部,即药柱在尾部受到的压力始终大于其头部,这从图12与图13也可以看出。
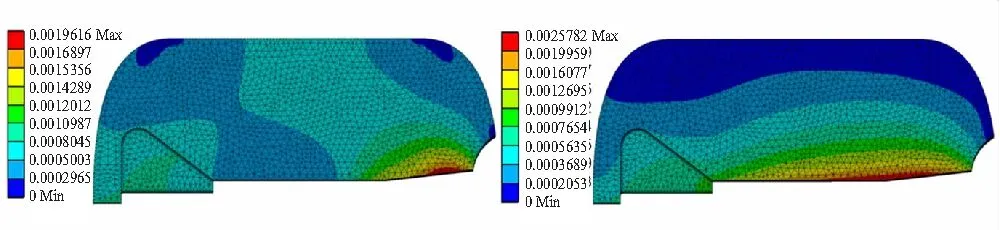
(a)t=13 ms (b)t=64 ms
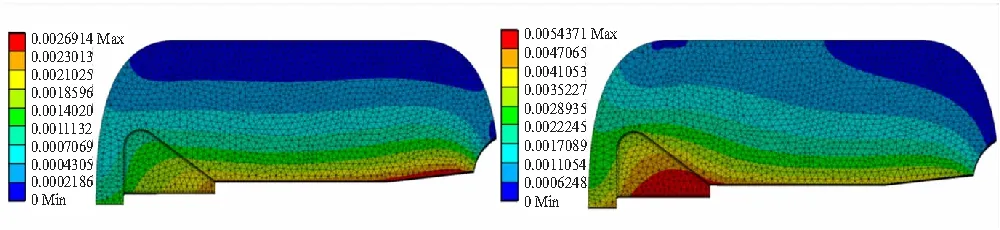
(c)t=69 ms (d)t=136 ms
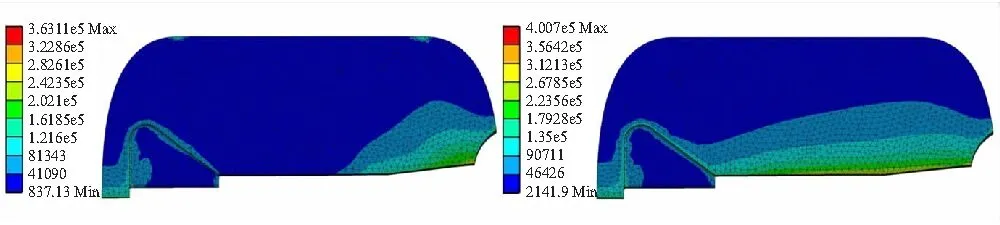
(a)t=13 ms (b)t=64 ms
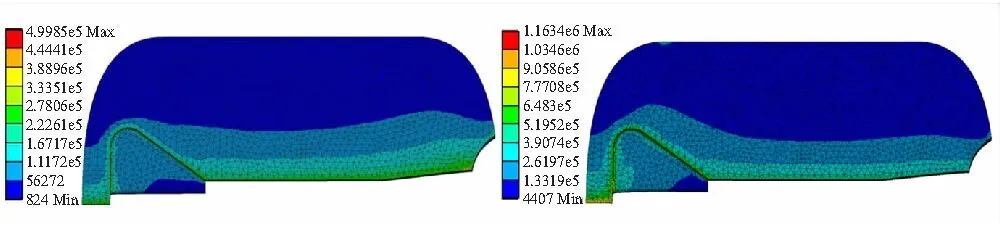
(c)t=69 ms (d)t=136 ms
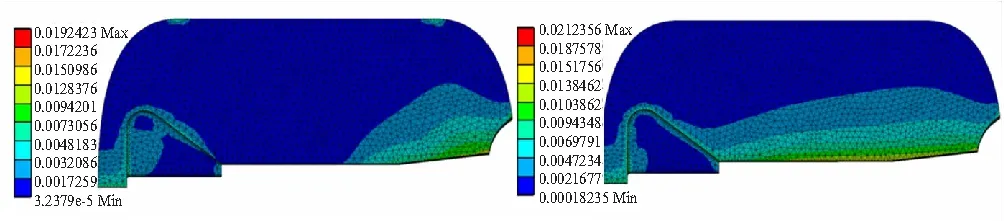
(a)t=13 ms (b)t=64 ms
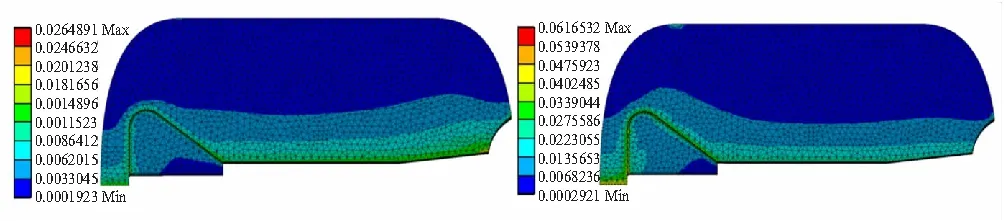
(c)t=69 ms (d)t=136 ms
堵盖打开后,由图11中的=69 ms和=136 ms时刻云图可知,药柱最大变形量发生的位置逐渐从尾部向头部移动,当流场基本达到稳定的流动状态时,即=136 ms时刻所对应的状态,药柱最大变形量约5.4 mm,位置在翼槽的侧面,这也证明了前面关于结构场变形很小,基本不会对流场流动状态产生影响的假设的正确性。堵盖打开后,使得燃烧室堵盖附近压强突然下降,但由于此时燃烧室内整体压强较高,整个药柱内表面压强受堵盖打开影响很小。因此,整个药柱内表面应力分布比较均匀,且沿径向逐渐降低,如图12、图13中=69 ms及=136 ms时刻云图所示。
在=136 ms时,燃烧室内压强基本已达到工作压强,该时刻沿翼槽对称面与药柱内表面交线的应力、应变分布曲线如图14所示,最大应力约1.16 MPa,对应最大应变约6.2%,发生在图中点所对应的位置。对于无缺陷的固体推进剂在内压载荷作用下,其破坏准则一般采用八面体剪切应变准则:
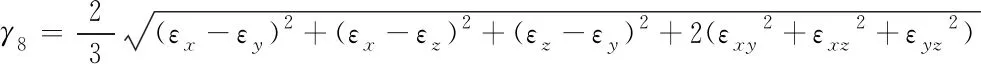
<()
(8)
式中为临界值;为安全系数。
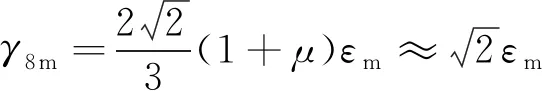

式中为该固体推进剂的泊松比,=0.498;为图13与图14所示的等效应变。
该推进剂单向拉伸最大延伸率≥40%,当安全系数取为5时,等效应变的最大值6.2%<8%,即<(15)。因此,药柱的结构完整性满足要求。
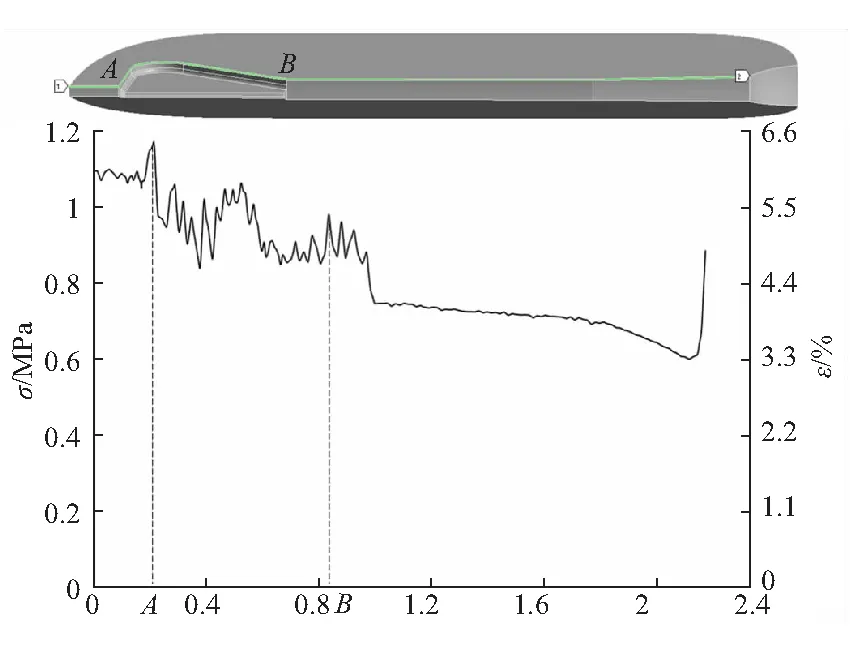
图14 t=136 ms沿图中特征线应力、应变曲线
3 结论
(1)点火燃气喷入燃烧室后,形成的复杂的多个涡流会很快的进行融合,最终在药柱的管型装药段及各个翼槽内各融合为一个稳定的涡流,且在喷管堵盖打开之前,该流动状态会一直保持稳定。因此,在发动机研制中,需要重点考虑点火燃气刚喷入燃烧室的几个毫秒。
(2)翼槽内燃面的扩展方向主要取决于其内部燃气的流动方向,与燃气流动方向一致。
(3)点火过程中,由于喷管堵盖的作用,会使药柱尾部所受应力大于其头部,当喷管堵盖打开后,整个结构场应力沿轴向分布比较均匀,沿径向逐渐降低,且应力及应变的最大值发生在翼槽与管形药柱段的过渡处。因此,在实际发动机药柱设计时,应注意堵盖附近及药面形状过渡处药柱的强度。
由于计算时间及计算机硬件的限制,本文没有对整个点火过程进行流固双向耦合计算,有待于进一步研究。

