基于概率统计的复合材料壳体的可靠性分析①

王 莹，张爱华，李 侃

(中国航天科技集团有限公司四院四十一所，西安 710025)

0 引言

在确保固体火箭发动机可靠性的基础上，降低其结构质量对于提高飞行器性能和降低成本都具有十分重要的意义。为此，设计人员在传统固体火箭发动机设计计算模型和大量工程试验的基础上，从可靠性分析方法上进行了不断的改进和尝试。固体火箭发动机的可靠性是指在给定工作条件下，能使发动机性能保持在允许范围内，不发生发动机失效的能力，通常包含结构可靠性和性能可靠性。航天结构可靠性设计可通过结合航天结构试验数据统计分析、可靠性分配、可靠性预测、可靠性设计和可靠性评估，达到提高航天产品质量、经济效益、设计水平的目的。

美国在发展阿波罗计划期间，为节约成本，对固体助推器的可靠性进行了仿真研究，到20世纪80年代末，该仿真方法已在各种固体火箭发动机上正式使用。可靠性仿真技术的出现使得固体火箭发动机的地面试车次数大大降低。国内也在不断地发展可靠性设计分析方法。1986年，冯连胜采用韦伯分布描述了超高强度钢制成的固体火箭发动机金属壳体的破坏应力分布，并估算了固体火箭发动机壳体的结构可靠性。1988年，王松柏提出固体火箭发动机壳体的强度与温度、时间等因素相关，进而分别采用半随机和全随机过程对固体火箭发动机壳体的动态可靠性设计方法进行了论述。1991年，张国安报道了这一种考虑固体火箭发动机壳体静力破坏和壳体材料断裂韧性要求的壳体厚度可靠性设计方法。结果表明，壳体厚度存在一个最佳范围，并非越大越好。1992年，黄世荣采用正态分布描述壳体的结构参数和力学参数，并引入可靠性安全系数(平均强度与平均载荷之比)对固体火箭发动机壳体结构进行设计。可靠性安全系数法既有可靠性设计的科学性，又具有类似于传统安全系数法的方便性。通过可靠性安全系数设计固体火箭发动机壳体，能够在保证固体火箭发动机结构可靠性的同时又能优化固体火箭发动机的结构质量。1995年，王铮推导了具有随机变量指数的发动机工作压强和燃烧室壳体弹塑性爆破压强的均值、标准偏差的表达式，得到了传统安全系数与可靠性概率的关系。任国周等以某固体发动机壳体强度作为结构可靠性主要因素，依据研制过程中积累的大量试验数据，对评估发动机结构可靠性的总体变异系数法和样本变异系数法进行了探讨，并举例对某产品的结构可靠性进行了计算和评定。1996年，谭三五报道了基于网格理论的复合材料壳体结构可靠性数字仿真方法及程序。该仿真方法结合伪随机数法和试验修正法描述固体火箭发动机复合材料壳体的各项参数在均值附近的波动。此篇报道预示着国内固体火箭发动机数字仿真工作的起步。2002年，徐志高等研究了金属固体火箭发动机壳体的可靠性数字仿真及其程序，并用混同法产生的伪随机数对壳体的可靠性进行了仿真计算。2005年，陈顺祥等利用随机有限元对具有随机因素影响的复合材料结构进行分析及可靠性计算，并在此基础上进行可靠性优化设计的探讨。2006年，沈军进行了CFRP缠绕压力容器在缠绕工艺过程中和内压作用下的可靠性研究，编制了基于MATLAB的Monte Carlo可靠性计算软件，实现了CFRP缠绕压力容器可靠性分析与设计，并通过水压爆破试验进行了验证，最终在大量试验基础上，推导出了CFRP压力容器的可靠性安全系数。2009年，路智敏等从薄膜理论和网格理论推导出的公式出发，结合碳纤维缠绕复合材料压力容器的爆破试验，分析了CFRP固体火箭发动机壳体爆破压强变异系数和其他参量变异系数的关系。同年，路智敏基于无力矩理论及弹性失效设计准则中的第一强度理论，利用可靠性设计中的二阶矩法分别推导出了球形壳体、椭球形封头、蝶形封头及锥形壳体的可靠度表达式。2019年，林峰等在考虑复合材料回转结构中各参数和载荷随机性的基础上，利用有限元软件以某航天用压力容器为算例，建立了该结构的可靠性分析模型，实现了该复合材料回转结构的随机可靠性预测分析和优化设计。罗惠敏等采用JC法(可靠度计算方法)和第四强度理论，推导了压力容器椭球封头和薄壁圆形筒体的可靠度计算公式，并采用ANSYS中蒙特卡洛可靠度计算方法，对上述公式的正确性进行了验证。

为保证可靠性，采用传统的安全系数法设计发动机复合材料壳体时，通常选取较高的安全系数，使得发动机壳体的质量占据发动机消极质量的较大比例。为了在保证壳体使用性的基础上，适当减轻发动机壳体的质量，过去的研究对固体火箭发动机壳体的可靠性设计和可靠性分析进行了理论研究。但针对固体火箭发动机复合材料壳体，未见基于大量试验数据统计的可靠性分析。本文首先对某复合材料发动机壳体的爆破压强和发动机最大工作压强进行了梳理统计。在此基础上，根据固体火箭发动机壳体的可靠性设计方法，得到了纤维缠绕壳体设计的概率安全系数。进一步根据概率安全系数计算了发动机壳体设计的概率安全裕度。本文的结论是基于试验结果统计分析得出的，对固体火箭发动机复合材料壳体结构的可靠性设计具有一定的参考价值。

1 发动机壳体可靠性设计基本理论

假设固体火箭发动机纤维缠绕壳体的性能参数与发动机最大工作压强均服从正态分布，根据可靠性理论可知，壳体结构可靠性概率公式可化为标准正态分布，即壳体结构的可靠性概率为

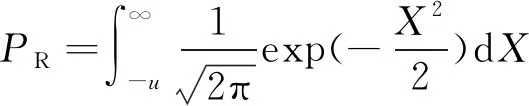
(1)

或者

(2)

其中，为概率系数(即积分限)，可表达为

(3)

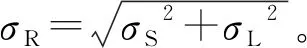
概率安全系数与、的关系式为=/，将其代入式(3)，可得概率安全系数与概率系数的关系式为

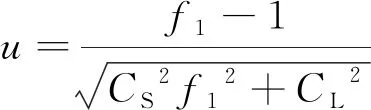
(4)

式中为壳体内压爆破压强的变异系数，=/；为发动机最大工作压强的变异系数，=/。

对式(4)两边取平方后整理，可得(-1)+2+-1=0，继而对该一元二次方程求解可得

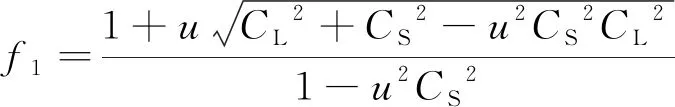
(5)

可靠性概率与概率系数的对应关系可由正态概率积分得到，见表1。可根据壳体设计中的可靠性概率要求，由表1中查出概率系数的值，结合根据试验获取的壳体内压爆破压强的变异系数和发动机最大工作压强的变异系数，并由式(5)计算概率安全系数，进而对壳体结构进行可靠性设计。

2 可靠性分析及设计

2.1 纤维缠绕壳体可靠性分析

为了研究发动机结构设计的可靠性，对某发动机的试车结果和其复合材料壳体内压爆破试验结果的数据进行采样。将统计的壳体内压爆破压强子样取平均值，并将各子样除以平均值，以进行归一化。采用同样的方法处理发动机最大工作压强，可得到图1所示的归一化壳体内压爆破压强和图2所示的归一化发动机最大工作压强。

表1 可靠性概率与概率系数的关系

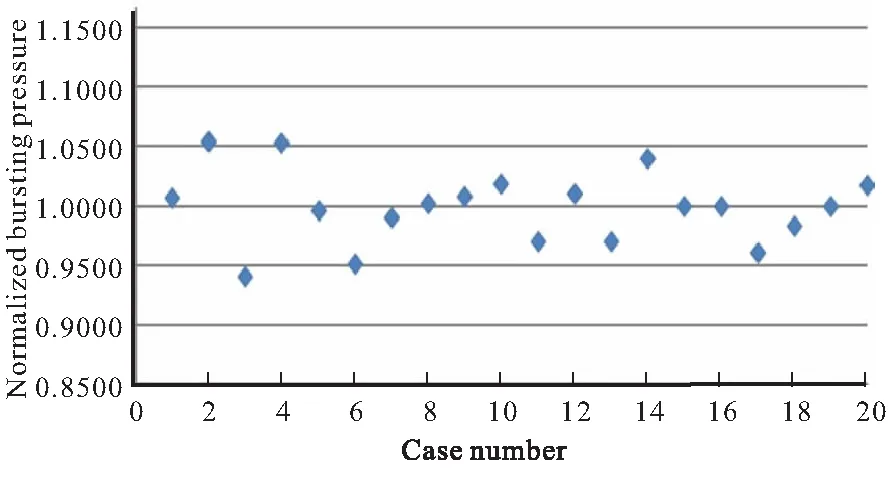
图1 归一化壳体内压爆破压强分布

图2 归一化发动机最大工作压强分布

根据图1和图2中的数据，可得到归一化爆破压强和归一化最大工作压强的均值、标准差、变异系数，如表2所示。

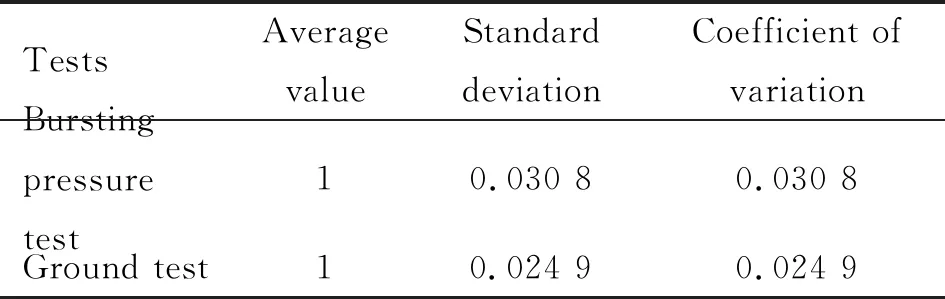
表2 归一化爆破压强、最大工作压强的均值、标准差、变异系数

将表2中的数据代入式(5)中，可得图3所示的壳体概率安全系数与壳体结构可靠性概率关系的柱状图。图3中，实测平均安全系数为实测发动机壳体爆破试验的平均爆破压强与实测发动机试车试验的平均最大工作压强之比，也即传统的安全系数。相对于实测平均安全系数，概率安全系数更小。当壳体结构可靠性概率为0.999～0.999 999 99时，在1.126 1～1.232 9的范围内。可见，根据传统安全系数设计法设计的发动机安全性更高，但依据概率安全系数法设计的发动机，既保证了壳体结构的可靠性，又具有质量更轻、相对更节约成本的特点。

同时，根据概率安全裕度和概率安全系数的定义，可得两者的关系式如下：

=-=(-1)·

(6)

进而可得到图4所示概率安全裕度与可靠性概率的关系图。图4中，实测平均安全裕度为实测发动机壳体爆破试验的平均爆破压强与实测发动机试车试验的平均最大工作压强之差。可见，相对于实测平均安全裕度而言，根据概率安全系数设计的壳体概率安全裕度较低。

2.2 纤维缠绕壳体设计示例

复合材料壳体采用平面缠绕时，理论缠绕角为

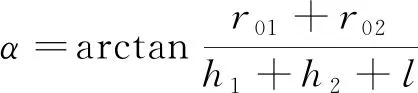
(7)

式中为壳体前开口半径；为壳体后开口半径；为前封头高度；为后封头高度；为筒段长度。

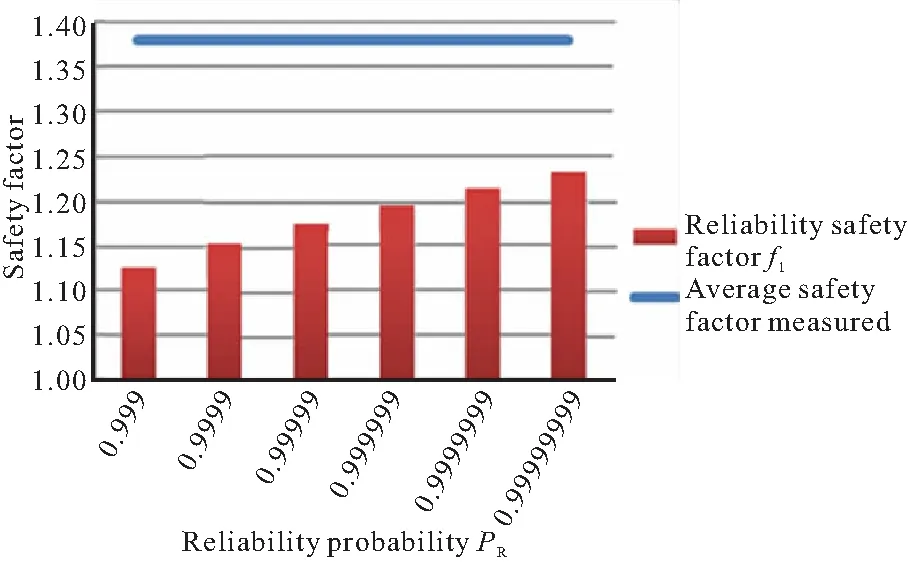
图3 安全系数柱状图

图4 安全裕度柱状图

由网格理论，壳体筒段纵向纤维厚度：

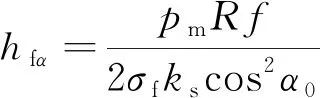
(8)

环向纤维厚度：

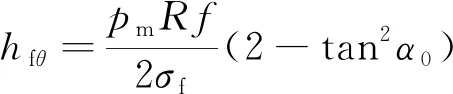
(9)

式中为发动机最大工作压强；为应力平衡系数；为纤维发挥强度。

假设壳体参数：=200 mm；=250 mm；=230 mm；=245 mm；=1000 mm；=9 MPa；=0.65；=2000 MPa；=400 mm。

将壳体参数、、、、代入式(7)，可得到纤维缠绕角为=17°。根据不同的可靠性要求在图3中选取概率安全系数，再将、、、、、代入式(8)和式(9)，可得到壳体筒段纤维缠绕纵向厚度和环向厚度。

通常要求壳体结构可靠性概率在0.999及以上。当取实测平均安全系数为1.377 9时，纤维纵向厚度和环向厚度分别为2.12 mm和2.36 mm。取壳体结构可靠性概率为=0.999时，概率安全系数=1.126 1，概率安全裕度为1.134 9 MPa，相应的纤维纵向厚度和环向厚度为1.73 mm和1.93 mm。

若纤维密度为1.5 g/cm，且不考虑胶含量，那么采用实测平均安全系数时，壳体筒段质量为16.88 kg；当取概率安全系数=1.126 1，壳体筒段质量为13.81 kg。可见，相对于采用实测安全系数的情况，采用概率安全系数时，壳体筒段的质量降低了18.21%。

不同可靠性概率下，壳体筒段质量减轻百分比的计算结果见表3。根据计算结果可知，若采用概率安全系数设计壳体结构，在确保壳体可靠性的同时，能够显著减少发动机的消极质量，在壳体结构可靠性概率为0.999～0.999 999 99的条件下，壳体筒段质量能够降低10.46%以上。

表3 不同可靠性概率下的壳体筒段质量减轻的百分比

3 结论

(1)相对于采用传统安全系数法设计的发动机而言，采用概率安全系数法设计的发动机，其消极质量较低，壳体筒段质量能够减轻10.46%以上；

(2)通过可靠性设计获得壳体结构可靠性概率在0.999～0.999 999 99范围内的概率安全系数为=1.126 1～1.232 9；

(3)壳体采用概率安全系数设计的概率安全裕度较实测安全裕度降低了38.39%以上(可靠性概率为0.999～0.999 999 99)。

采用传统的安全系数法设计，使得发动机的可靠性较高，但同时伴随较多的消极质量。建议根据实际使用、设计、生产具体过程，在充分考虑外载荷、药柱完整性等具体设计需求和影响因素的基础上，可适当地降低发动机壳体的安全系数。