一种改进的煤矿供电线路故障定位算法*

茹瑞鹏，郭志强，田锦绣，张昭亮，刘尚霖

(1.山西潞安矿业集团 慈林山煤业有限公司 李村煤矿，山西 长治 046000；2.辽宁工程技术大学 电气与控制工程学院，辽宁 葫芦岛 125000)

0 引言

煤矿产业是我国国民经济发展的重要支撑力量，煤矿生产的安全工作被国家高度重视。随着科学技术及应用的日益发展，各种安全检测设备和大型机械设备不断被投入使用，使得煤矿供电系统的运行维护更加具有挑战性。其中，多由电缆组成的供电线路是煤矿供电系统中的重要部分，而煤矿井下环境恶劣，导致供电线路易发生短路或断路故障，同时人工方法排查存在困难，且效率低下。随着数字信号技术的快速发展，行波定位法因其原理简单、不易受过渡电阻影响且测距精度有保证，在故障定位中得到广泛应用[1，2]。

由于煤矿供电系统的复杂环境，收集到的故障行波信号中易存在噪声干扰，而准确确定行波到达监测装置的时刻又至关重要。为提高强噪声运行条件下行波法故障定位的准确度，提出一种改进的煤矿供电线路故障定位算法。供电线路故障发生后，通过变分模态分解(Variational Modal Decomposition，VMD)算法与广义S变换(Generalized S Transform，GST)对故障行波进行信息提取。利用Teager能量算子(Teager Energy Operator，TEO)对提取出的信号进行分析，继而获得故障位置。

1 故障行波的变分模态分解方法

1.1 故障行波的相模变换

由于三相输电线路中电压与电流常见的相互耦合现象，导致提取的故障行波在反映故障特征时可能存在偏差。为消除三相耦合现象带来的影响，将三相故障行波解析成三个独立的模分量，即通过相模变换方法消除模分量中三相耦合的不良因素。通过分析相模变换后的α模分量，可以获得更加完整的原始故障信号特征。

1.2 故障信号变分模态分解

为提取输入信号中的有效特征信息，通过构造和求解变分问题，迭代更新模态分量的中心频率和带宽，将行波信号适应性地分解为具有不同的中心频率和有限带宽的模态分量[3，4]。

将问题转化为寻求估计带宽之和最小的函数模型，可以得到处理有约束的变分问题的公式如下：

(1)

其中：f(t)为原始信号；j为复数单位；t为时间；δ(t)为单位脉冲函数；uk(t)为f(t)分解出的模态函数；{uk}={u1,…,uk}为最终的k个模态分量；{ωk}={ω1,…,ωk}为各个模态分量的中心频率。

在求解上述变分问题的过程中，先进行时域到频域的转换，同时经过反复化简和对问题的求解，再在傅里叶逆变换的基础上，进行从频域到时域的转换，继而得到各个模态分量的中心频率和带宽[5]。

1.3 k值的选取

煤矿供电线路发生故障时产生的故障行波中存在许多频率不同的信号及大量噪声，在利用VMD算法对信号进行分解的过程中，需要指定最终获取到的模态分量的个数，即k值。通过实验测试不同k值下的分离效果，选出合适的k值，才能有效分离噪声，同时分解出有足够识别能量的模态量，从而更有效地提取故障分量中的信息特征。

2 故障定位算法

经VMD分解后得到的模态分量在对信号中噪声进行了有效过滤的同时也保留了信号中的有效特征，但仅通过VMD算法无法获取行波到达记录点的时刻，且模态分量中的频率分量仍然比较复杂。

2.1 S变换故障定位算法

为对模态分量进一步精确分解，采用高斯窗宽度与频率倒数成正比关系的S变换，在有效保留原始信号特征的同时，也达到了避免选择窗函数、弥补窗口宽度固定缺陷的目的[6,7]。信号x(t)的S变换如下:

(2)

(3)

其中：τ为时间轴上的平移因子，通过τ调节高斯窗在时间轴t上的位置。观察式(3)高斯窗口函数，可以发现，高斯时间窗宽度与频率成反比。通过对信号进行S变换可以得到保留原始信号有效特征信息的S模矩阵，利用对S模矩阵进行S逆变换可重构原始信号。其逆变换为：

(4)

通过S变换，可以实现将行波信号在频率的尺度上进行精确分解，但由于S变换中的窗函数固定，若应用中信号波动过于剧烈，则可能无法被S变换有效处理，所以需要对S变换更进一步调整以增强其时频分辨率。

2.2 广义S变换故障定位算法

为增强信号中时频分辨率，引入调节因子g(g>0)，根据不同的信号频谱灵活调整高斯窗函数，将信号分解为更具体的频率分量的同时有效保留其变化特征，即广义S变换。

由于S变换中高斯标准差公式σ(f)=1/|f|，则频率确定后，高斯窗形状仅与时间相关。为调节高斯窗的宽度，新定义σ(f)=g/|f|，并将其代入式(2)中，可得GST表达式如下：

(5)

其中：g为高斯窗宽度拉伸因子。随着g的取值不同，所得信号中时频分辨率变化情况如下：

(6)

如此，通过改变g的取值来调整高斯窗形状，以增强GST处理后信号的时频分辨率，提高其调节性、自适应性。

GST在继承S变换优点的同时，通过引入高斯窗幅度拉伸因子g实现对获得的S模矩阵时频分辨率的灵活调节，以革除传统S变换中高斯窗函数固定的弊端[8，9]。GST可以在更广的范围上实现对频率分量的精细调整，使提取频率分量和识别行波波头突变点的操作更加方便有效。

2.3 能量算子改进的故障定位算法

由于提取出的S模矩阵包括众多单一、精细的频率分量，为有效获取调节后的模态分量的瞬时能量变化，引入Teager能量算子对提取出的频率分量进行分析。TEO计算简单，实时性强，在分析信号的瞬态冲击时有较好的时间分辨率，适用于信号的实时检测处理[10]。

若信号为s(t)，TEO可定义为：

Ψ[s(t)]=s′2(t)-s(t)s″(t).

(7)

其中：s′(t)为s(t)的导数；Ψ为能量算子。

对于离散信号s(n)，式(7)可近似表示为如下形式：

Ψ[s(n)]=s2(n)-s(n+1)s(n-1).

(8)

通过TEO对经过VMD-GST调解过的单分量频率信号进行调解，从而得到检测信号的瞬时幅值与瞬时频率，其中瞬时能量谱峰值所对应的时刻即为故障初始行波到达监测点的时刻。

3 改进的供电线路故障定位算法流程

故障定位流程如图1所示。供电线路故障点产生向线路两端传播的行波，并被线路端点的录波装置捕获。通过变分模态分解算法对行波信号进行分解，获得有足够识别能量的模态分量，有效滤除行波中噪声。利用广义S变换，在频率尺度上对行波信号进行精确分解，获得保留有效特征信息的S模矩阵，同时引入调节因子实现对S模矩阵时频分辨率的灵活调节。通过Teager能量算子对S模矩阵中模态分量进行分析，获得瞬时能量谱峰值所对应的时刻。利用在线测量法测出实时波速。将瞬时能量谱峰值所对应的时刻与测得的波速代入双端行波测距公式，获取故障位置。

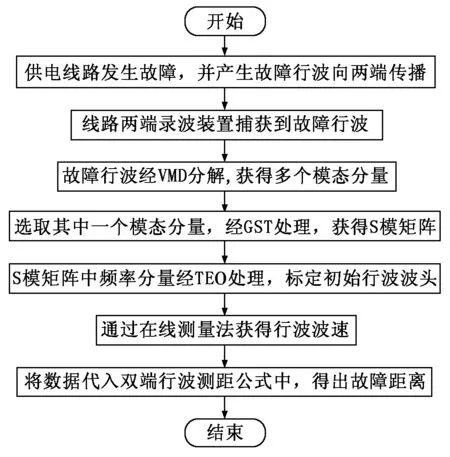
图1 故障定位流程图

4 仿真验证

图2是在PSCAD/ETMDC环境下建立的某煤矿井下供电系统仿真模型。

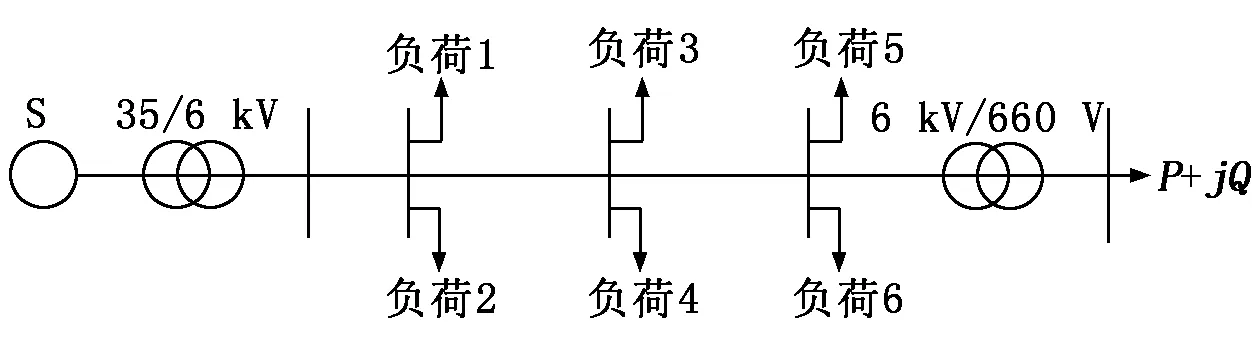
图2 供电系统仿真模型

仿真模型中，供电线路为频率相关模型，总长12.7 km。假设A相单相接地故障发生在距送电侧10 km处。故障发生后，送电侧和负荷侧A相的电流电压波形分别如图3、图4所示。

图3 送电侧A相电流

图4 负荷侧A相电流

对A相电流经相模变换得到的模分量进行k值为3的变分模态分解，结果如图5、图6所示。

图5 送电侧模态分量

图6 负荷侧模态分量

综合各模态分量表现，选取模态分量2为输入信号。利用经Teager能量算子改进的广义S故障定位算法，获得保留有效特征信息的S模矩阵，获取瞬时能量谱，如图7、图8所示。

图7 送电侧瞬时能量谱

图8 负荷侧瞬时能量谱

由图7、图8得，线路两端获取行波的时刻分别为：送电侧t2=5 034，负荷侧t1=5 009，采样频率为1 MHz。通过对波速实际测量，测得行波波速v=2.98×105km/s，代入测距公式d=(L-v(t2-t1))/2之中，得:

(9)

由式(9)计算出的故障点到送电侧的距离dM=10.075 km，与实际值10 km相差0.075 km。因此该改进的故障定位算法应用于单相接地时具有较高准确度。

5 结论

综合考虑了故障行波在线路中传播的实际情况，提出一种改进的行波分析方法，并将该方法应用于煤矿供电线路故障定位中。该方法从故障行波中提取出的信号具有较强的噪声鲁棒性与自适应性。处理后的模态分量的时频分辨率更灵活、范围更广。同时，行波波头抵达线路两端时间点的定位更加可靠、准确。仿真数据表明，该算法在应用于煤矿供电线路中单相接地故障情形时具有较高的精度。