基于改进匈牙利算法对多人人体关键点匹配的研究*

邬春学，贺欣欣

(上海理工大学 光电信息与计算机工程学院，上海 200093)

0 引言

人体姿态估计是计算机视觉任务中重要的一部分，与人体检测、识别、跟踪等相关技术息息相关，其主要研究如何准确快速地定位人体关键点，并确定各个关键点所在的人体目标[1]。目前存在着传统的定位方法与基于深度学习的方法，它们对推动计算机视觉的研究起着重要的作用。

基于深度学习的检测方法又可分为自上而下(Top-down)和自下而上(Bottom-up)的方法。Top-down检测方法的思想是先识别出图像中的所有人体，然后检测每个人的关键点[2]，但随着图像中人数的增加，Top-down方法的计算成本显著增加，此时则需要考虑使用Bottom-up方法保持稳定。Bottom-up检测方法的思想是先计算出一个图像中所有人体的关键点，然后再将这些关键点通过匈牙利算法、信号聚类等方法划分给不同的目标人体[2-4]。本文基于自下而上的2D多人人体姿态估计，对求解关键点匹配算法进行研究。

在复杂和多人的环境下，传统的匈牙利算法面临着关键点遮挡、算法性能等关键问题。本文基于2017年提出的PAFs理论基础以及OpenPose模型，针对关键点联系和匹配模块，提出了一种改进的匈牙利数学模型进行实验。改进的算法采用亲和度向量场与邻接矩阵结合的方式，通过对矩阵内的数值处理求解最佳匹配，即输出正确的人体姿态框架图。

1 相关工作

1.1 人体姿态估计的发展

传统的人体关键点定位方法基于人体姿态模板库，图像特征信息到模板库中姿态的映射通过特定的映射通道实现。在此基础上，针对人体姿态是千变万化的特点，学界提出了图结构模型，此方法突破了模板库的局限性，使得人体姿态估计方法更加灵活。并且继Felzenszwalb等人[5]关于人体姿态估计的变形零件模型(DPM)的开创性工作之后，许多算法被提出以改进DPM体系结构[6]。Yang等[7]提出了一种使用支持向量机建模的混合模板，Johnson等[8]通过使用身体部分检测器的级联提出了更多的鉴别模板，Pishchulin等[9]提出了基于DPM的高阶身体部位依赖性模型，使用Poseletprior和DPM模型[10]捕获身体部位的空间关系。以上所有方法的共同特征之一是它们可以使用手工制作的立体特征(例如边缘、轮廓、HoG的特征和颜色直方结构图)，与学习特征相比，这些特征被证明具有较差的泛化性能和判别能力[11]，因此针对复杂环境下的特征提取，这些方法的性能是不够的。

基于深度学习的方法与传统方法相比较，引入了卷积神经网络(Convolutional Neural Network，CNN)来解决姿态估计问题。Toshev[12]等提出的Deeppose和一系列CNN姿态回归器使得精度显著提高。Wei[13]等提出了卷积姿态机(Convolutional Pose Machine，CPM)——一种多阶段估计方法，来解决神经网络层数太深产生的梯度消失问题。Papandreou[14]等提出了G-RMI方法，使用Faster R-CNN自上而下地进行多人姿态估计。此外还有Mask R-CNN[15]、RMPE[16]和Simple Baselines[17]等方法。主流的自下而上的方法有PAFs[18]、DeepCut[19]以及Associative Embedding[20]。与自上而下不同的是，这些算法先检测出图像中所有的关键点，然后将这些关键点关联和分组于归属的人体，即实现关键点检测和聚类。

2017年，来自CMU感知计算实验室的曹哲等人[18]发表了一篇使用PAFs(Part Affinity Fields)实时预测2D人体姿态的论文，PAFs是对肢体进行标注，表示人体每个肢体的2D向量，同时保持了肢体区域之间的位置信息和方向信息。图1为一个肢体PAFs的示意图。如图所示，若点P在这个肢体上时，则关键点j1、j2连线方向上的为单位向量(模长为1)，否则为零向量。判断条件如式(1)和式(2)所示。

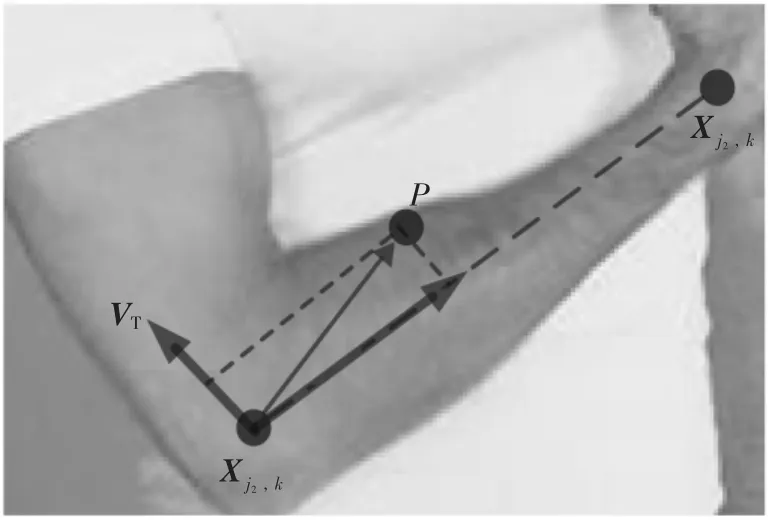
图1 单个肢体PAFs示意图

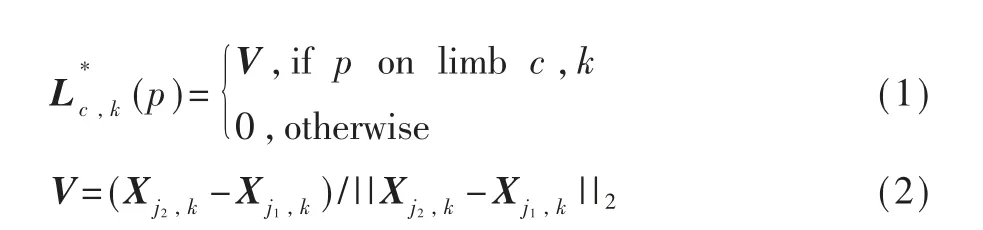
在此理论基础上，美国卡耐基梅隆大学(CMU)基于卷积神经网络和监督学习，并以Caffe为框架开发实现了OpenPose人体姿态识别项目。其中实现的基本原理是输入一幅图像，经过卷积网络得到一组特征图，然后分别使用CNN网络提取置信度(Part Confidence Maps)和亲和度向量场(Part Affinity Fields)，最后基于PAFs把多人关键点匹配转换成图论问题，采用匈牙利组合算法求解一种类似二分图匹配的问题，最终组成一个完整的人体姿态结构。

1.2 基础模型的构建

本文基于OpenPose人体姿态估计模型提取人体的骨骼关节点和肢体，对解决两类不同肢体集合互相连接的匈牙利算法进行了优化，提高了模型在复杂场景下匹配肢体时的性能。OpenPose模型的网络结构如图2所示。

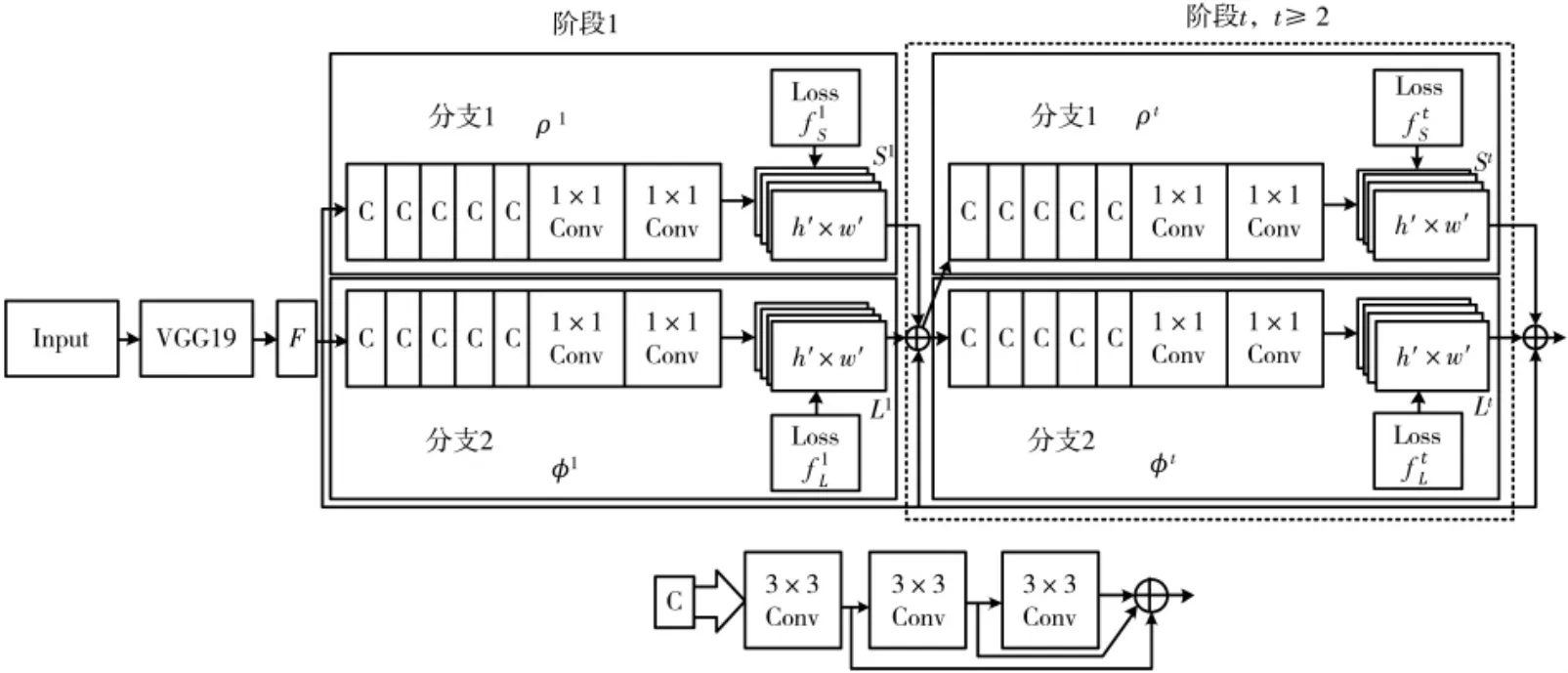
图2 OpenPose网络结构

OpenPose网 络 结 构 中，3个 连 续 的3×3卷 积 核组成了卷积块C的网络，与原始网络中7×7卷积核不同。图像经过网络提取特征，得到一组关节点和肢体的图像特征图F，然后特征图F作为之后卷积神经网络的输入。其中，第一阶段中用于推断的卷积网络分别为ρ1和φ1，分别对图像特征F进行处理，且ρ1、φ1、ρt和φt都 包 含5个 卷 积 块 与2个1×1的卷积。S是置信度网络，用来预测关节热度图，L是亲和度向量场网络，用来预测关节亲和域。

第一阶段的置信度和亲和度向量场如式(3)、式(4)所示：

第二阶段及之后的置信度和亲和度向量场如式(5)、式(6)所示：

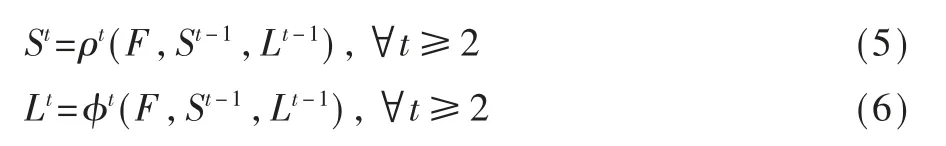
对检测出来的置信度图执行非极大值抑制，获得离散的关键点位置候选集如图3(a)所示。由于图中有多人，对于每种关键点有若干候选，如图3(b)所示，针对全连接图的求解问题是十分复杂的，于是本文将全连接图划分为若干个子集。利用PAF网络的大感知场，成对关联分数隐含地编码了全局上下文，再通过匈牙利算法实现二部图图3(c)到图3(d)的过程，取得最佳匹配。图中表示部件j2集合中的顶点1，同理表示部件j3集合中的顶点2表示j2与j3是否有关联。

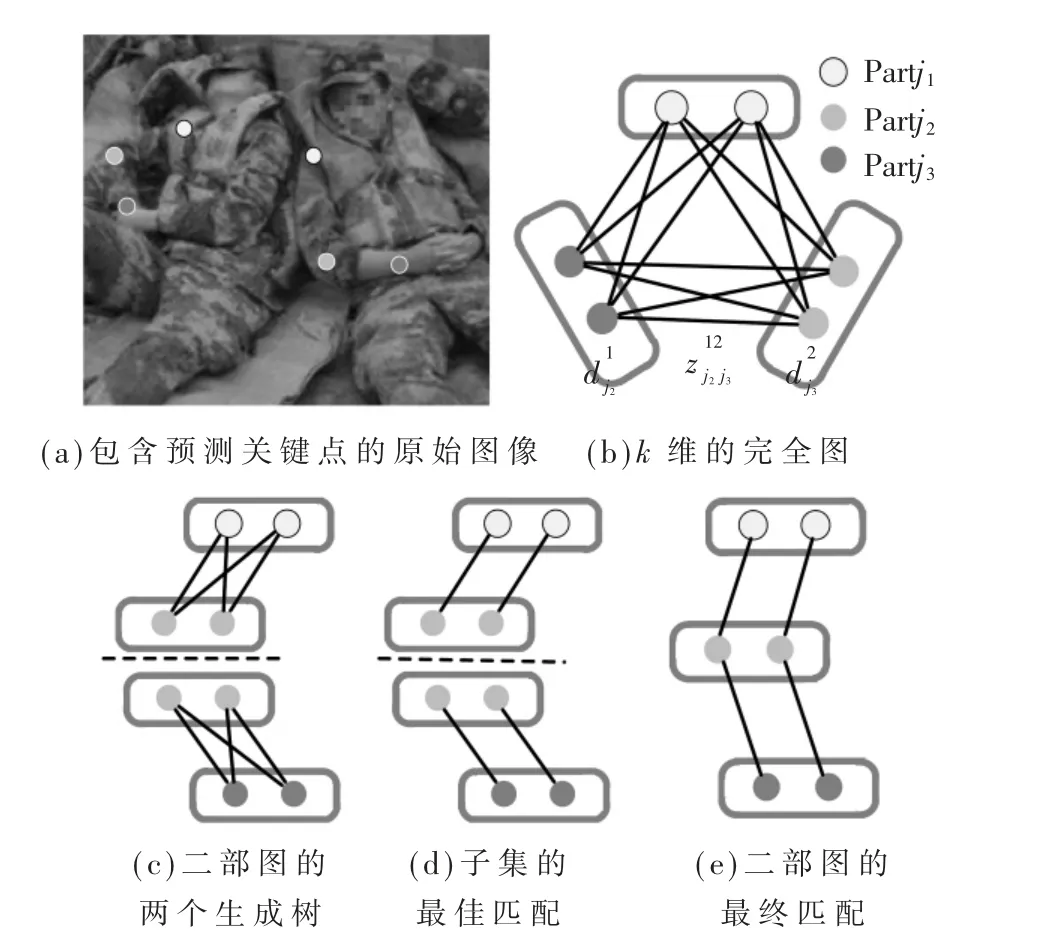
图3 图的匹配

2 改进的匈牙利算法

2.1 经典匈牙利算法

匈牙利算法是由匈牙利数学家Edmonds于1965年提出的，它可以用于求解多种形式的匹配问题。在实际应用中，若在有权二部图中，顶点所连接的边权重不同，要求在顶点匹配的同时考虑总权重最大或者最小的问题，这就是最优匹配问题。建立数学模型如下：设用wij＞0(i，j=1，2，…，n)表示集合A中的顶点i匹配集合B中的顶点j时的权重，定义决策变量：

则问题可以转化为：

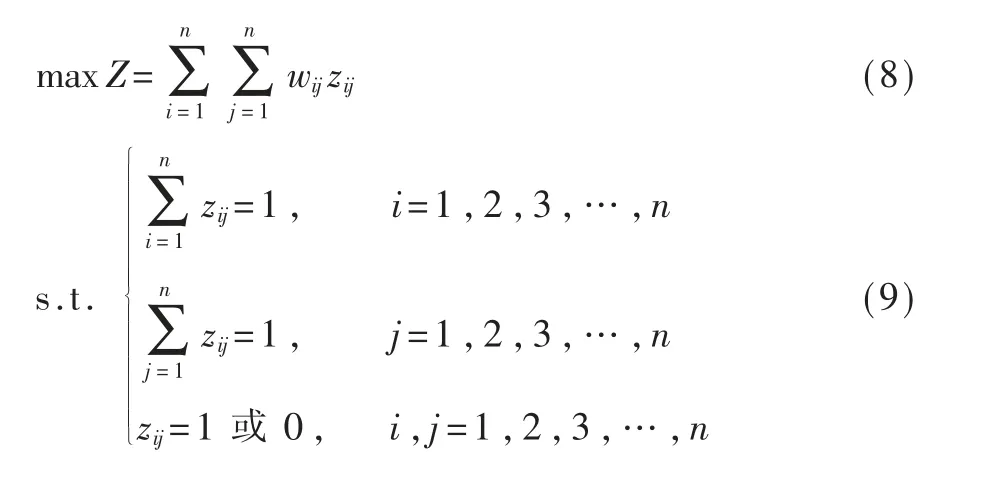
定理1：如果从有权匹配矩阵E(eij)的每一行的元素中分别加上或减去一个常数ui，也可称作该行的位势；从每一列的元素中分别加上或减去一个常数vj，也可称作该列的位势，得到一个新矩阵F(fij)，若其中fij=eij-ui-vj，则二者的最优解等价。

定理2：若矩阵E的元素可分成零和非零两类数字，则覆盖零元素直线的最大数量等于位于不同行、不同列的零元素的最大个数。

由上述定理可总结出匈牙利算法的基本思想是：通过符合定理不断变换的方式，使得矩阵E的行和列尽可能多地生成零元素，直到能从变换后的矩阵中找出n个位于不同行、不同列的零为止，这些零元素对应的zij=1，其余元素对应的zij=0。

2.2 改进的数学模型

在关键点分配中存在一定时间范围内资源数目和匹配任务不等的问题，可能造成两类关键点在进行配对时出现误判或者漏判的情况，因此可以用改进匈牙利算法将不平衡的匹配问题转化成平衡匹配问题。

现有如下二部图匹配问题：共有m个待匹配的二部图，其中每个二部图中的集合各有n个顶点待匹配，考虑到每两个顶点在匹配时，所产生的连接方向上的积分以及整个二部图的权重和不同，建立数学模型如下：

首先计算出两点(dj1，dj2)连线上的线性积分，若的方向与Lc(p)方向一致，则E的值会越大，表明该位置是一个躯干的可能性就非常大。

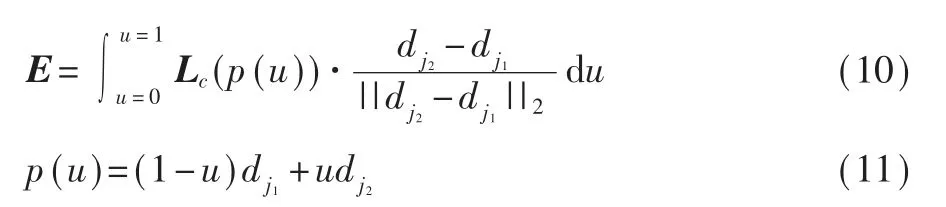
定义决策变量：

则问题可以转化为：

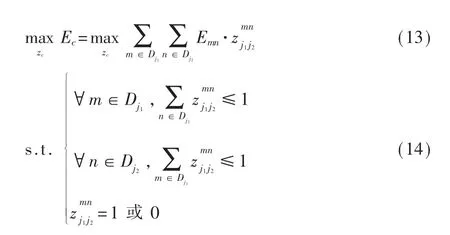
2.3 算法步骤及流程图

由于原匈牙利算法的不足，本文提出改进匈牙利算法结合邻接矩阵求解最大匹配，它的实现步骤如下：

(1)将原始二部图中边的权重取反，构建初始化邻接矩阵。

(2)对邻接矩阵进行变换，每行(列)都减去各行(列)的最小值，此时每行(列)至少都有一个0。

①作最少的直线覆盖住邻接矩阵中所有的0元素，且直线只能是某一行或者某一列上的，不能跨越不同的行或列。若有元素被两条直线覆盖，标记上x*。

②判断是否需要终止循环，判断条件为第一步中作得的直线数是否等于各集合中的顶点数，若相等则终止循环继续步骤(4)，否则继续操作。

③对邻接矩阵中的元素作变换得到更多的0元素。具体步骤为：首先将所有没有被直线覆盖的元素记作Φ，在Φ中找到最小的元素，记作k；然后将Φ中的所有元素都减去k，并将标记上x*的元素都加上k。

(4)输出变换后的邻接矩阵，从只有一个0元素的行或者列开始，将这个0元素标记为0*，这样做的目的是确保本行或列的顶点一定有另一个点做匹配，然后将0*所在的行和列中的其他元素忽略。对于出现多种同一列或同一行的独立零的情况，根据次小值越大对其行或列中的零元素优先匹配。反复选取之后，矩阵中的0*分别处于不同的行且分布在不同的列中，则代表此次最大匹配已完成，0*对应的顶点即为匹配的结果。改进的匈牙利算法的流程图如图4所示。

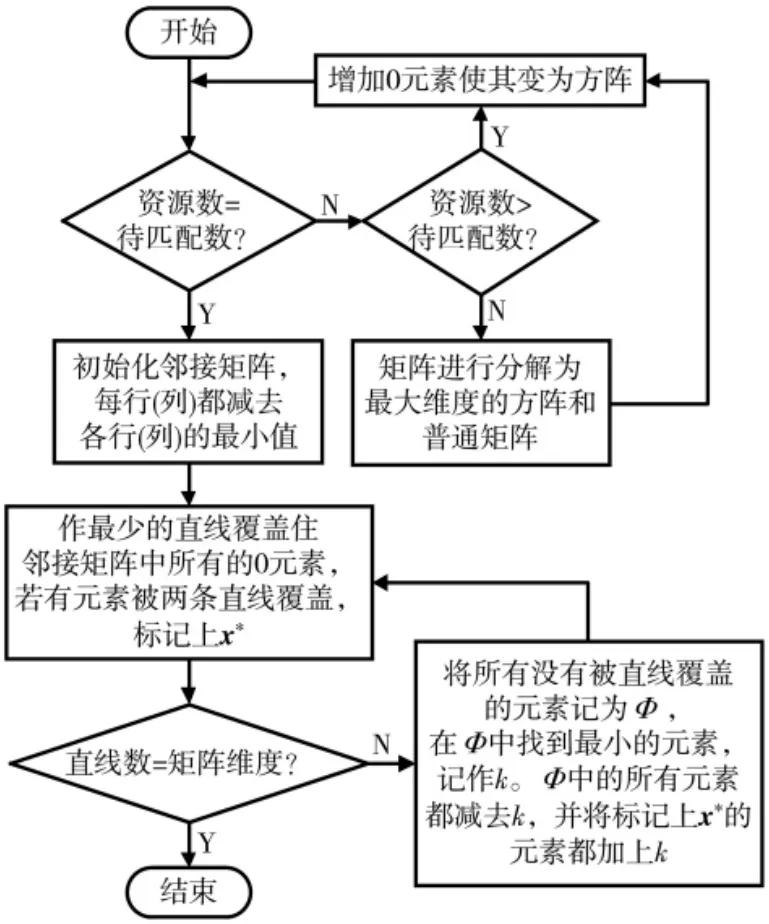
图4 改进的匈牙利算法的流程图

图5和图6给出了算法的两个示例，有助于理解算法的计算过程。

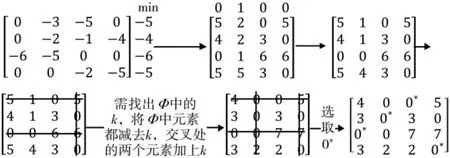
图5 示例1

图6 示例2

3 实验与分析

为了验证改进匈牙利匹配算法的性能以及在人体关键点匹配中求解最佳匹配的可行性，本文实验首先将改进的匈牙利算法与未改进的匈牙利算法在求解m×n阶矩阵最佳匹配时消耗的时间和计算误差进行对比，之后选取100张包含多场景、多人的图像输入原始TensorFlow版本的模型和搭载了改进后匈牙利算法的模型进行处理图像的对比实验。实验采用的操作系统是Windows 10，其他设备信息是Intel®CoreTMi7-8700K CPU@3.70 GHz，64 GB内存以及NVIDIA GeForce 1080Ti显卡，基于Python3.5编程设计语言完成应用模型设计实验。

由于企业公允价值确认在大多数时是一个估计的结果，所以，其在企业实际应用过程中极易被利用成为操纵利润的工具。同时，企业会计准则不是一种技术手段，不同准则会生成不同的企业会计信息。企业公允价值变动被计入到当期损益之中，其对企业的实际经济收益情况造成了改变，比如当企业交易性金融资产公允价值发生变动时，其将会使得企业产生经济利得或造成经济损失，从而改变企业的短期投资，且只确认了资产的减值，并未确认资产的升值收益；而企业衍生金融工具，其不但能够增加企业的资产或负债，同时还能够直接对企业当期损益情况造成影响。

在本次实验中，为评测改进算法的性能，分别测量改进算法和未改进算法在运行过程中占用内存的时间，首先使用代码自动生成k个m×n且均匀分布的随机数矩阵，然后通过对k个矩阵分别进行10次、50次、100次求解，将累计计算的平均运行时间进行比较，可更加直观地看出两种算法在运行时间上的差距。

通过分析表1的数据，能够较为直观地发现相对于经典算法，改进算法能够在较短时间内完成相同的任务量。

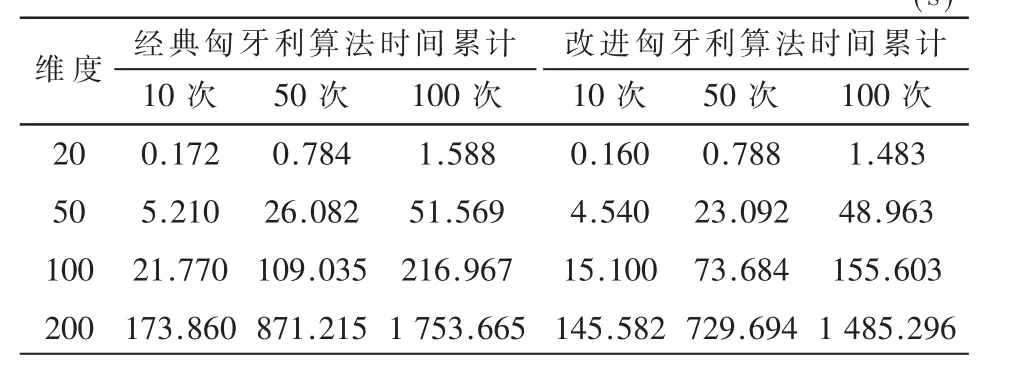
表1 两种算法的平均累计时间 (s)

在对改进匈牙利算法的精确度分析上，把得到的目标函数值与真实值的差以及矩阵维数作为分析的主要指标。下面分别使用两种方法对15维、50维、100维、200维 的 矩 阵 进 行10次、50次、100次的反复计算，得到改进算法误差绝对值累计数据与误差率，如表2所示。

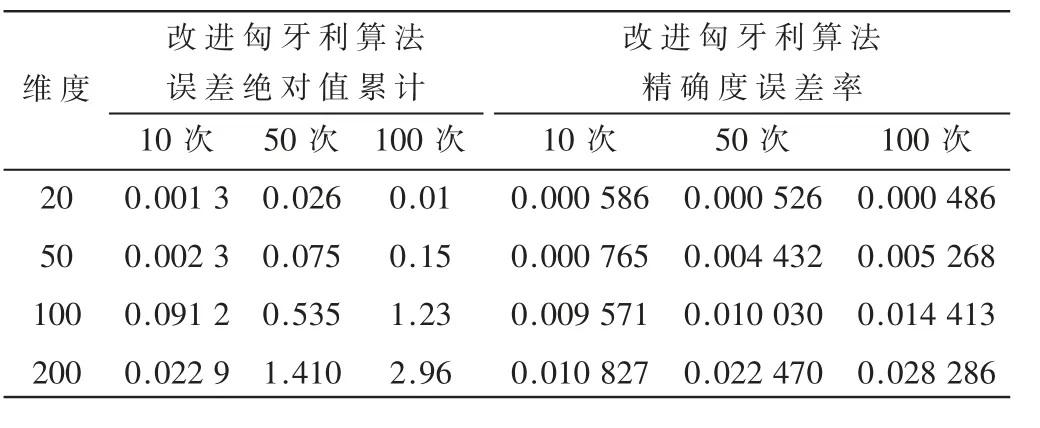
表2 改进算法的精度分析

通过分析表2的数据，能够较为直观地发现：改进后的算法在求解100×100以内矩阵的全局最优值时，存在着微小的误差，同时随着矩阵维数的增加，精确度的误差率有微小的增加波动。

实验最后进行了原始TensorFlow版本的模型和搭载了改进后的匈牙利算法的模型处理图像的对比实验。所选图像包含多人且人物与背景不易区分，在经过模型处理后分别输出结果图，部分结果如图7所示，图8显示了两种模型在运行时CPU的负载情况。

图7 多人图像测试对比结果

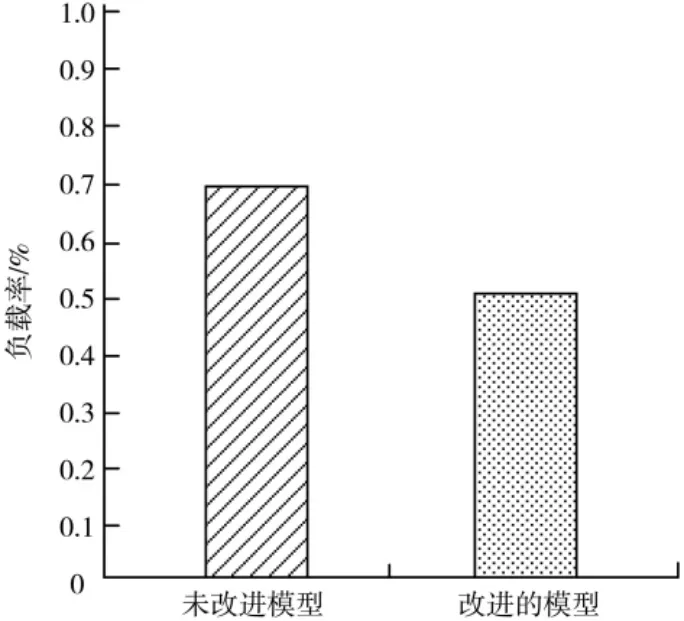
图8 不同模型对计算机的负载率对比

从实验结果可以看出，在处理相同图像的情况下，搭载了改进的匈牙利算法的模型相对于未改进的模型关键点匹配正确率提升了至少40%，尤其是对多人下肢的匹配性能有明显的提升，并且运算速度较之前至少提升5%，且对计算机的负载率降低20%。

4 结论

通过研究在关键点匹配背景下的合理求解最佳匹配问题，提出基于改进匈牙利算法的二部图邻接矩阵求解最佳匹配的方法，同时综合考虑了在不同维度矩阵下两种算法的运行时间、改进算法的精确率，解决了传统匈牙利法在人体关键点匹配中复杂度高、耗时久、网络结构冗余等问题，为待匹配候选点的多对多匹配提出了一种新的思路，实现了关键点的合理、有效分配，提高了模型整体效率。

后续研究将重点关注如何在占用更少的硬件资源和软件资源的基础条件下，加快批量提取各种人体姿态图像特征，以及在检测所得到的人体图像基础上如何进行图像SLAM的研究。