基于改进VIKOR的攻击效果评估算法

宿振宇，卢 凯

(华北计算机系统工程研究所，北京 100083)

0 引言

随着科技的不断发展进步，计算机网络已经广泛应用到了各行各业，大量新型互联网产品和服务应运而生，与此同时，计算机网络的安全问题也随之而来，网络安全威胁日益凸显，有组织、有目的的网络攻击形势愈加明显，为网络安全防护工作带来了更多挑战。研究网络攻击效果评估，对深入研究攻击原理与技术和提高抵御网络攻击能力两方面都具有重要意义。

1 相关研究

网络攻击效果评估一般分为以下几个步骤：首先构建合理的指标体系，其次确定指标的权重，最后计算评估结果。

目前已有国内外学者对网络攻击效果评估这个课题进行了一定研究。在评估指标的建立方面：胡影等人研究了网络攻击效果的提取和分类，定义原子功能作为攻击效果的基本单位,提出了原子功能提取的原则[1]；汪生等人提出了可对多种技术进行攻击效果评估的指标体系，给出了单个使用和联合使用攻击模型进行效果评估的方法[2]。在评估算法的改进方面：张义荣等人提出了网络熵的概念，给出了基于网络信息熵的网络攻击效果定量评估模型[3]；李雄伟等人提出了模糊层次分析法(Fuzzy-AHP)，解决了一致性检验难问题[4]；王会梅等人在评估中引入粗糙集理论，对属性的重要性进行度量，不依赖于先验知识，但该方法对样本数据的要求较高[5]；Jajodia等人考虑评估的关联性，将灰色系统理论应用于网络攻击效果评估中[6]。

在水利工程、供应链绩效评价等领域内还有一种基于数学模型的评估算法——多准则妥协解排序法(VlseKriterijumska Optimizacija I Kompromisno Resenje，VIKOR)，VIKOR方法的基本思想是：基于理想点并利用折衷优化思想对备选方案进行排序[7]。此方法未曾在网络攻击效果评估领域中有所应用，但其采用的多准则决策折衷优化思想也适用于网络攻击效果评估这个课题。

综上所述，目前存在一些可行的算法，但大都基于层次分析法，在此方法中，不考虑各个指标因素之间的相互关系，认为各个指标之间是相互独立的，但在评价网络攻击效果时，各指标总会相互影响。因此本文引入网络分析法(Network Analysis Process，ANP)，使用DEMATEL-ANP方法建立网络结构[8-11]，考虑指标之间的相互关系，将各攻击类型从特征指标和性能指标两个方面建立攻击效果评估体系，并采用VIKOR和灰色关联分析相融合的方法对攻击效果进行评估。

2 网络攻击效果评估模型构建

2.1 评估指标构建

本文从基础指标和攻击的特征指标两个方面来建立指标体系[12-13]，将网络攻击分为以下四大类：流量分析、篡改、恶意程序、拒绝服务。相对应地，将特征指标细化为以下几个原子功能：探测信息、破坏数据、权限控制、拒绝服务。在被攻击机受到一种或多种网络攻击时，只需选取对应的原子功能，即可对攻击效果进行度量。本文构造的网络攻击效果评估指标体系如图1所示。

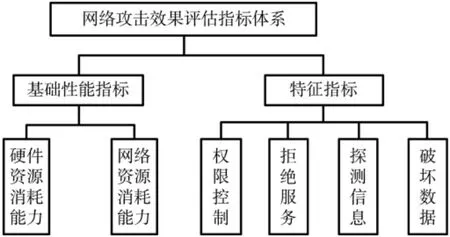
图1 评估指标体系

2.2 评估模型构建

2.2.1 DEMATEL-ANP模型

首先，从采取的模拟攻击实验出发，确定指标所用的原子功能，采用DEMATEL方法思想，将各指标之间的关联度进行量化，将指标i对指标j的影响程度在合适的标度内进行度量得到aij，矩阵主对角线代表指标与自身的关联度，其值均为0，可获得直接影响矩阵O：

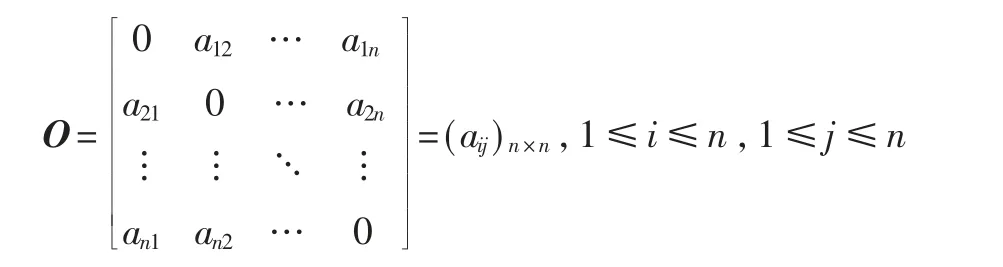
然后，在上述直接影响矩阵O的基础上，通过归一化计算得到规范化直接影响矩阵N：

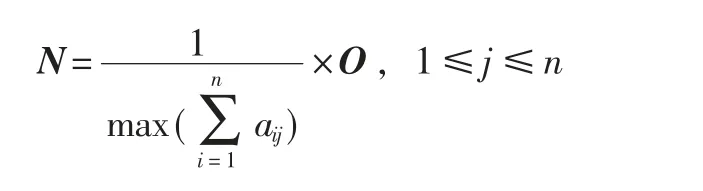
接下来，由上述的规范化直接影响矩阵N，计算得到综合影响矩阵T。规范化直接影响矩阵自乘,表示的是要素之间增加的间接影响，当把所有的间接影响都加起来的时候有如下公式：

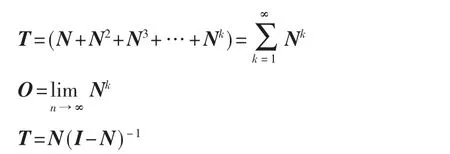
其中，I为单位矩阵。

由上述计算得出的综合影响矩阵T，可以通过下文计算得到各个要素的影响度、被影响度、中心度、原因度。

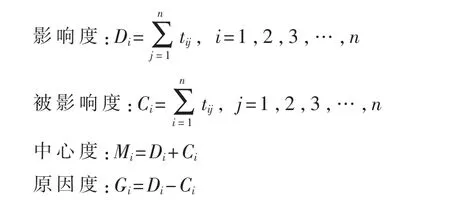
接下来，采用ANP方法的思想，将矩阵T每列进行归一化处理获得加权超矩阵W。

为了能够准确反映各指标间的相互关系，以加权超矩阵为基础，通过稳定性处理，得到最终的稳定超矩阵W′：

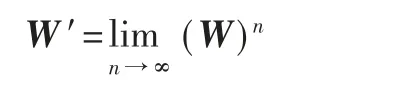
如果上述极限收敛且唯一，那么所得的极限超矩阵W′的所有列向量将是相同的，而此时的列向量就是各指标的权重。

整个计算流程如图2所示。

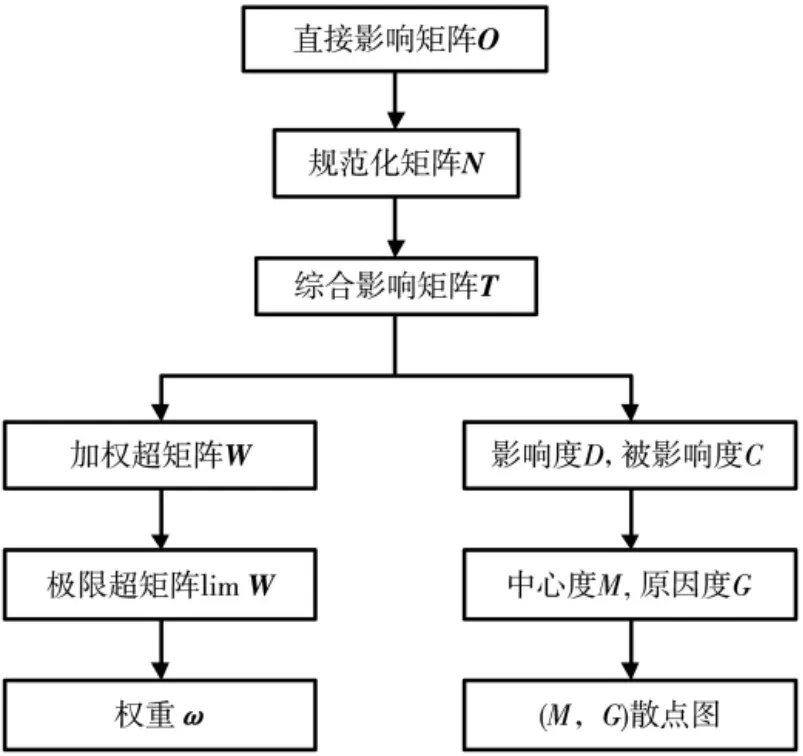
图2 权重计算流程图

2.2.2 VIKOR-灰色关联度模型

首先，对问题进行描述，在仿真平台模拟攻击，根据构建的指标体系进行数据采集，假设采集到m组指标，n次攻击的数据，利用m个指标对n个对象进行评价。fij表示在指标aj下对象Ai的值(i=1，2，…，n；j=1，2，…，m)，决策矩阵为F=[fij]n×m，对指标数据标准化后，得到标准化决策矩阵X=[xij]n×m：

根据得到的决策矩阵X确定正、负理想解，在这里参考VIKOR方法的思想，将正、负理想解用X+、X-来表示，那么就有：

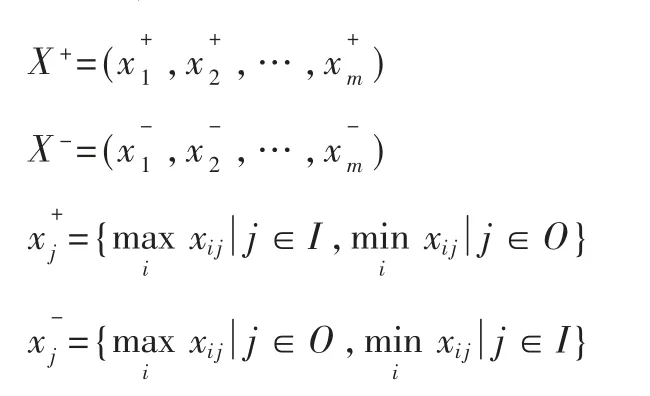
计算基于VIKOR网络攻击效果评估的效益值Si和遗憾值Ri：

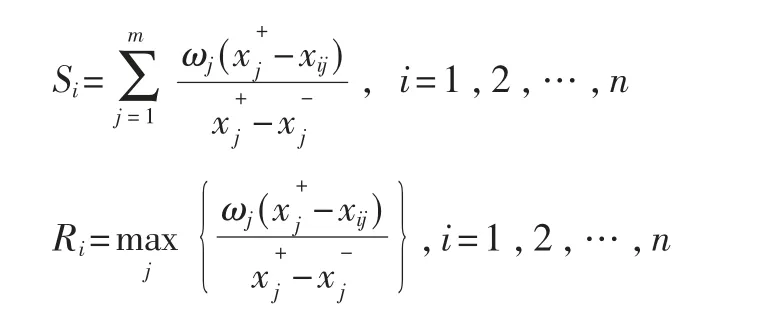
其 中，ωj是aj的 权 重。

Si的值越小，表明Ai的效益越高，也就是攻击效果越好；Ri的值越小，表明Ai的遗憾越小，也就是攻击成本越小。

接下来可以得到最大、最小效益值和遗憾值：

本文采用灰色关联分析的思想，将正理想解作为参考队列，待评估方案作为比较队列，那么在指标aj下对象Ai与正理想解的灰色关联系数为：

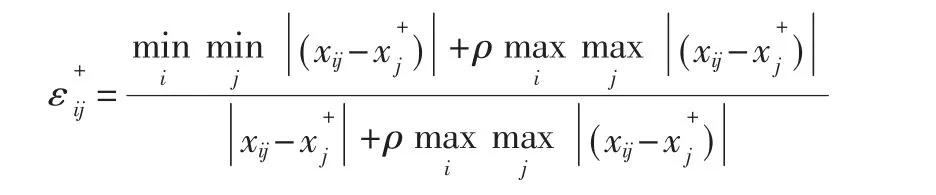
将负理想解作为参考队列，待评估方案作为比较队列，那么在指标aj下对象Ai与负理想解的灰色关联系数为：

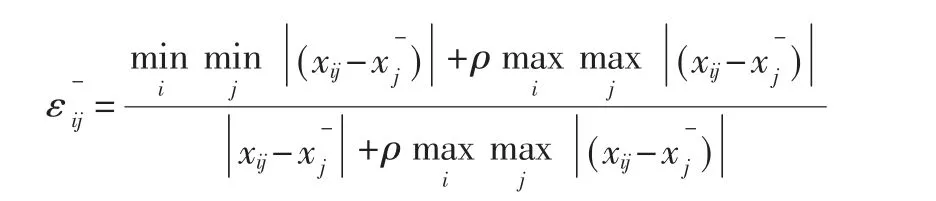
与正理想解的关联度为：

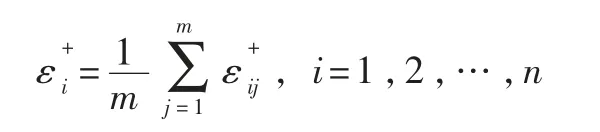
与负理想解的关联度为：

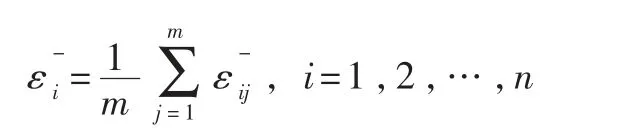
其中，ρ为分辨系数，一般取值为0.5。

接下来，计算基于灰色关联分析的待评估方案效益值si和遗憾值ri：

si、ri最大、最小值的确定：

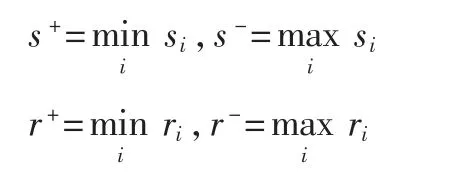
计算基于VIKOR和灰色关联分析的待评估方案综合指标Qi：

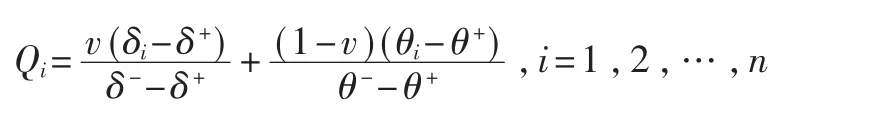
其 中δ+=S+×s+，δ-=S-×s-，θ+=R+×r+，θ-=R-×r-，δi=Si×si，θi=Ri×ri；v为折衷系数，一般取v=0.5，表示从均衡的视角进行描述。

分 别 利 用δi、θi、Qi的 值 对 方 案 进 行 排 序，值 越小排序越靠前。

确定最优折衷方案，设Qi(i=1，2，…，n)中最小值对应的方案为A1，次小值对应的方案为A2，若满足以下两个条件则A1为最优：

(1)Q(A2)-Q(A1)≥DQ，DQ=1/(n-1)；

(2)在δi和θi中至少有一个排序最为靠前。

如果有一个条件不满足，则得到一个折衷解集：

(1)如果满足条件(1)不满足条件(2)，则折衷解集为{A1，A2}。

(2)如果不满足条件(1)满足条件(2)，这时可以在满足不等式：Q(Ai)-Q(A1)＜DQ的i中取一个最大值imax，从而得到折衷解集为{A1，A2，…，Aimax}[14-18]。

3 实证分析与结果

本文以典型的DDoS攻击为例，证明所提出模型的合理性。首先在指标体系中选取合适的原子功能，DDoS攻击的主要影响在资源消耗和服务破坏两方面，因此选择硬件资源消耗能力、网络资源消耗能力、拒绝服务三个原子功能建立对DDoS攻击的指标集，本文将指标集定义为D，D={丢包率，响应时间，响应成功率，网络抖动，网络带宽占用率，内存使用率，CPU使用率}[19]。

3.1 指标权重分配

通过上文提出的DEMATEL-ANP模型，可以得到综合影响矩阵，从而得到各个要素的影响度、被影响度、中心度、原因度，如表1所示。

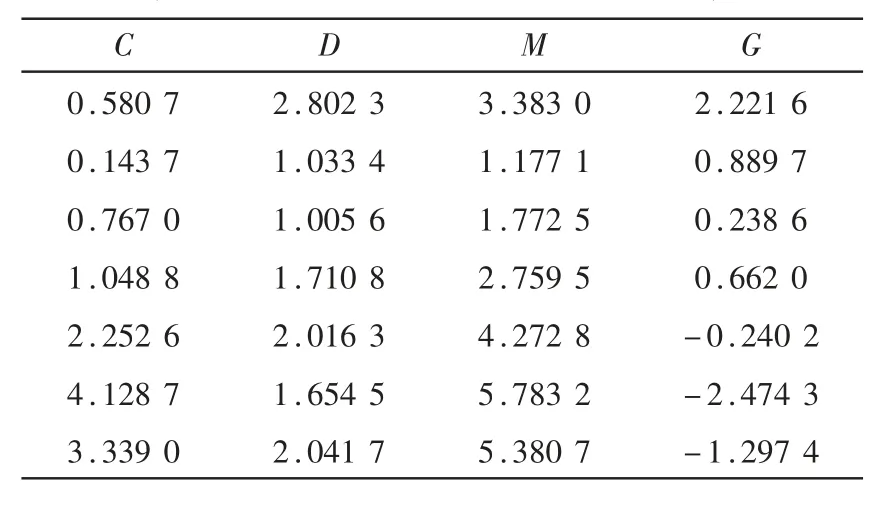
表1 指标元素相关度数据表

通过综合影响矩阵，可以计算得到稳定超矩阵，从而获得各指标的权重值如图3所示。

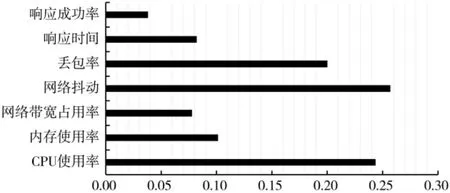
图3 指标权重分配图

3.2 网络攻击效果评估结果

实验采用UDP Flood攻击，设计具体的攻击方案[19-20]：

(1)在攻击机上部署LOIC攻击工具，采用wireshark观察UDP包攻击情况；

(2)在被攻击机上部署iperf和perfmon采集被攻击机指标数据，在虚拟机中安装Tomcat服务器；

(3)实验进行5次攻击，每次攻击持续时间为2 min，分别采集2 min后的攻击数据，启用攻击后持续访问Tomcat，观察其服务状态；

(4)为防止偶然性，进行多次实验，数据取其平均值，攻击强度通过增加攻击线程数量和加快攻击速度实现，实验强度为A1＜A2＜A3＜A4＜A5。

实验过程中获取的指标数据如表2所示。

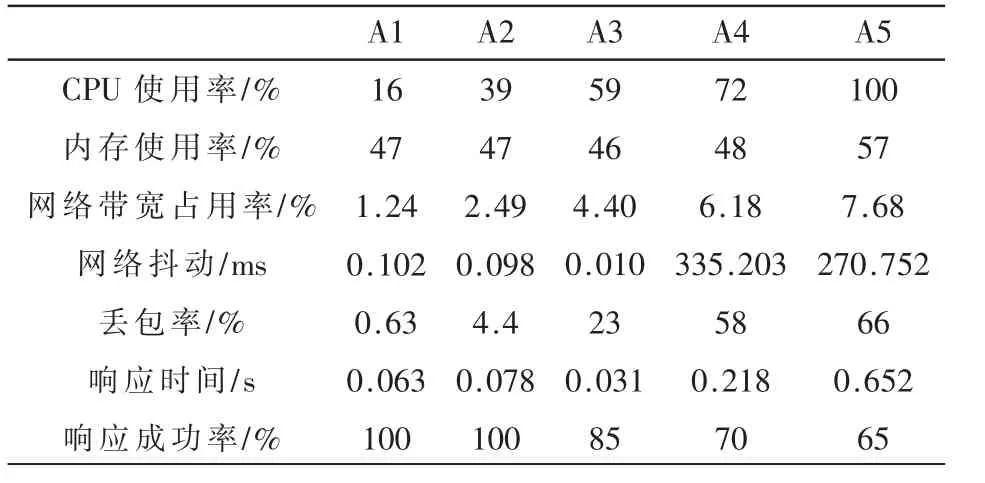
表2 指标数据

根据提出的VIKOR-灰色关联分析法可以得出待评估方案的期望值、妥协值以及基于灰色关联度的期望值和妥协值，如表3所示。

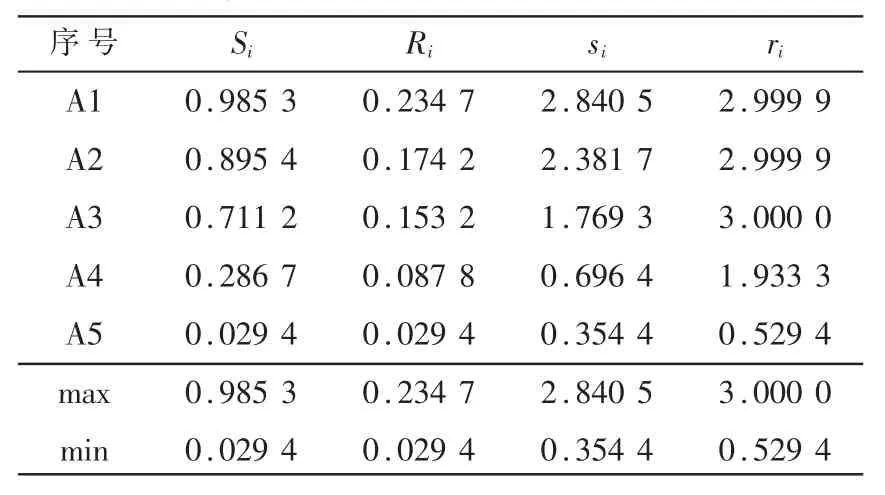
表3 期望值和妥协值

根据VIKOR方法的评价方法，通过期望值和妥协值计算得到综合指标，如表4所示。

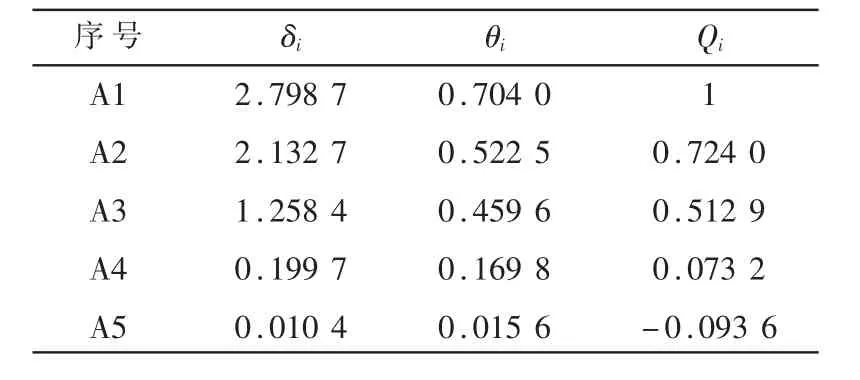
表4 综合指标

由表中数据可以得到5次攻击的效果排序为A1＜A2＜A3＜A4＜A5，与预先设置的实验攻击强度排序相符，由此可以证明本文算法的有效性和合理性。

在实际决策中，专家可能会有不同的主观态度，进而采取不同的折衷系数v，随着v值变化，排序可能会发生变化。本文设v∈[0，1]，步长设为0.1进行敏感度分析，验证评价模型的准确性。通过结果得知，在不同值下，5次攻击的排序不变，因此可以认定此模型对v扰动不敏感，进一步验证了模型的稳定性。

3.3 对比分析

本文使用目前比较流行的TOPSIS算法和灰色关联分析法作为对照，TOPSIS算法是一种被广泛应用的多属性决策方法，通过对待评估方案和正负理想解贴近度的考量来对所有方案进行评估排序，灰色关联分析法通过灰色关联度来考量待评估方案与最优解之间的关联关系，从而对待评估方案的效果进行描述[21-22]。对比本文算法，对5次攻击实验进行评估，分别得到各方法的综合评价结果，如图4所示。

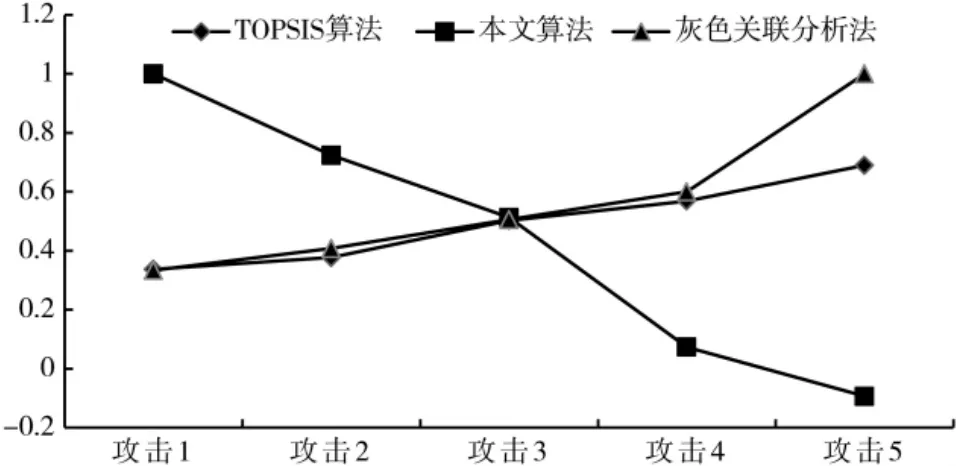
图4 算法对比图

因为本文算法是越小越好型指标，而TOPSIS算法和灰色关联分析法是越大越好型指标，因此折线图趋势不同。通过比较可以发现，本文提出的VIKOR-灰色关联分析评估算法与另外两种算法得出的结果一致，并与预先设置的实验攻击强度排序相符，因此可以证明本文算法的有效性。

与其他两种方法对比，本文所提出方法的优势如下：

(1)与TOPSIS算法对比：TOPSIS算法的核心在于比较待决策方案与理想点的距离。在TOPSIS算法中，不仅要考虑到与正理想解的最近距离，而且要考虑到与负理想解的最长距离，从而确定最优解，以最大限度地提高效益。但TOPSIS中的这些距离只是简单地求和，没有考虑它们的相对重要性，相反，VIKOR算法通过最佳化妥协提出了一个新的方法，决策者会考虑待决策方案与理想解距离的相对重要性，也考虑距离自身的权重，使用正负理想解概念，同时考虑各方案与正理想方案和负理想方案的贴近度。因此本文算法得到的妥协解更接近理想解。

通过对数据的分析可以发现，用TOPSIS算法得出的对各次攻击的评估值之间的相对差异较小，即评估值分布比较密集，而过度精确的排序会导致排序结果出现逆序，所以其得到的最终结果并不一定是最优解。而本文算法得到的评估值之间的相对差异较大，因此，当需要评估的样本数量比较大的时候，本文算法会表现出更大的优势。

(2)与灰色关联分析法对比：与本文所提出的方法相比，灰色关联分析法的主观性过强，且各方案的评估值差距较小。当待评估的攻击数量增加时，不利于评估者做出更加合理的判断。而本文算法对各次攻击的评估值区分度较大，更便于区分各次攻击的效果。

4 结论

本文针对网络攻击效果评估进行研究，提出了基于VIKOR-灰色关联度的网络攻击效果评估方法。该方法使用DEMATEL-ANP方法建立网络结构，考虑指标之间的相互关系，克服了传统的基于层次分析法的评估中不考虑指标间相互关联关系的问题，将各攻击类型从特征指标和性能指标两个方面建立了一套攻击效果评估体系，并将VIKOR和灰色关联分析方法相融合，提出VIKOR-灰色关联分析法对攻击效果进行评估，既弥补了灰色关联度从单一角度评估的问题，又弥补了TOPSIS算法不考虑自身权重、容易产生逆序的问题，并通过实验证明了该方法是有效的。