可伸缩式清仓机构的模态分析

黄金凤，王祎璠，于江涛

(1.华北理工大学 机械工程学院，河北 唐山 063210；2.河北省工业机器人产业技术研究院，河北 唐山 063210)

0 引言

煤仓的仓体部分一般为圆柱体结构，出料口下方多为圆锥形或双曲线形状，大部分煤仓都存在着不同程度的堵仓问题，主要表现为侧壁的粘壁现象以及漏斗椎体部分的结拱现象[1-3]。而人工清仓不仅效率低，而且严重威胁工人安全，为解决煤仓的堵仓问题，很多大型的清仓设备相继问世，但部分大型地面煤仓的直径较大而进煤口较小，导致很多大型的清仓设备无法入仓清理。本文所述的是一种具有伸缩功能的清仓机构，但由于清仓过程中末端执行器与堵塞物碰撞时会使机构本身发生振动，对机构本身结构造成影响，为避免产生共振现象，需要对可伸缩式清仓机构进行模态分析，得出清仓机构本身的固有频率与主振型[4-5]。本文利用ANSYS Workbench对振动系统进行离散化，添加适当的边界条件，最终得出可伸缩式清仓机构的振型与固有频率。

1 可伸缩式清仓机构几何模型的建立

可伸缩式清仓机构由驱动部分与伸缩部分构成，其中驱动部分由支座、移动平台、液压缸和液压杆组成，伸缩部分由4根伸缩臂构成，4根伸缩臂以液压杆为对称轴等间距分布，每根伸缩臂分别由内臂、中臂、外臂以及牵连板构成。其原理为液压杆与支座固接，液压缸与移动平台固接，工作时，液压缸运动带动移动平台进行运动，进而带动伸缩臂进行伸缩运动。相邻的臂之间通过末端的端座进行铰接，相邻的两个端座之间使用滚针轴承与轴相连接，端座两侧固接一对链轮，臂与臂之间的运动关系通过链轮与链条进行约束,支座上焊接有4个吊环螺栓，其上连接若干根钢丝绳，通过钢丝绳来控制清仓机构在煤仓内部的位姿变换。可伸缩式清仓机构完全收缩时直径为1.1 m，完全展开时可达范围为18 m。利用SolidWorks建立的可伸缩式清仓机构三维模型如图1所示。

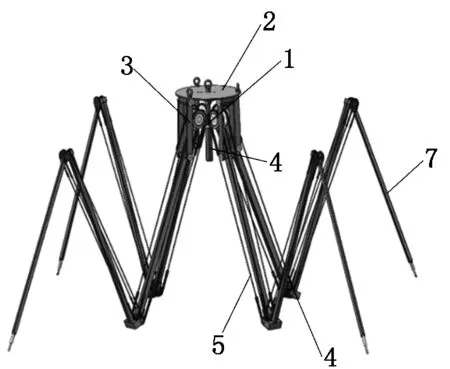
1-移动平台；2-支座；3-牵连板；4-液压缸；5-内臂；6-中臂；7-外臂

2 前处理

由于仅对机构中部分零件进行分析无法得出系统的整体性能，因此如果想得出清仓机构整体的动态特性，需要对其整体进行模态分析。因为可伸缩式清仓机构为1/4对称结构，为了方便分析与求解，取模型1/4的对称部分，并简化对分析结果影响较小的结构，如轴的垫圈、链轮、链条等，将轴和轴承的装配简化为销轴和孔的关系，将简化后的模型导入ANSYS Workbench中。首先根据对称面建立两个新的坐标系，然后根据两个新坐标系的XOY平面分别建立两组对称部分。

首先设置各零件材料属性，销轴的材料采用抗拉强度与屈服强度较高且耐磨性较好的合金钢40Cr，其密度为7 900 kg/m3，弹性模量为206 GPa，泊松比为0.33；除销轴外，其余材料均采用Q235钢，密度为7 800 kg/m3，弹性模量为206 GPa，泊松比为0.28。

对机构整体进行网格划分，设置网格大小为30 mm，为了使分析结果与实际情况更加吻合，对销轴与孔的接触面进行网格控制，设置接触面的网格大小为10 mm，使销轴外表面的节点与孔的内表面基本重合，最后生成的有限元模型如图2所示，其节点数为131 966，单元数为5 8471。

图2 可伸缩式清仓机构的有限元模型

3 加载求解

与结构不同，机构是一个几何可变体系，随原动件的位置不同，机构的具体姿态也不同，当原动件的位置确定后，机构就变成了结构。本文采用有限元法对机构特定位置进行模态分析，习惯上采用粘接的方式连接各个构件，从而代替转动副的作用，但这样虽然方便了建模与分析，但也使系统的刚度有所增加，分析结果与机构的实际情况有所差异。因此在对可伸缩式清仓机构的模态分析中，首先对各个销轴与孔的接触方式进行修改，将默认的绑定接触改为摩擦接触，摩擦因数μ设为0.2。然后再依次对销轴添加约束，约束其径向自由度，保留其切向自由度，以此来模拟销轴处的转动副。在此模态分析中，只考虑重力的影响，不涉及载荷的作用。

因为对清仓机构动态特性影响较大的频率主要集中在低频区，高阶模态对其影响较小，所以本文只在0～100 Hz内提取模态，定义输出可伸缩式清仓机构前6阶固有振型。

4 模态计算与分析

利用ANSYS Workbench对可伸缩式清仓机构进行模态分析，得到的前6阶振型如图3所示，前6阶固有频率如表1所示。

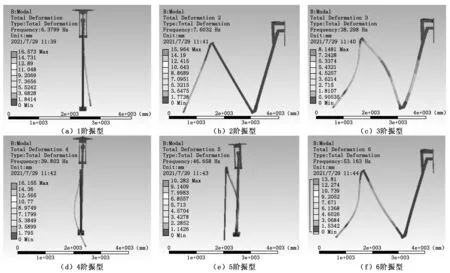
图3 可伸缩式清仓机构前6阶振型

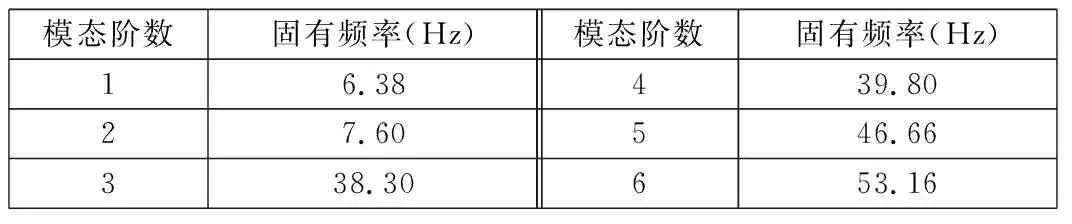
表1 清仓机构前6阶固有频率

由表1可以看出，可伸缩式清仓机构前6阶固有频率逐渐增加，在6.38 Hz～53.16 Hz之间。

由各阶振型可以看出：

(1) 第1阶振型主要集中在外臂上，表现为外臂在Y轴方向上的侧摆，振动的最大位移在外臂末端位置，为16.57 mm。该振动会增大外臂端座与中臂末尾端座之间的压应力，使二者的接触面磨损与变形。

(2) 第2阶振型也集中在外臂上，表现为绕中、外臂连接处销轴的转动，方向沿顺时针方向，振动的最大位移在外臂末端位置，为15.96 mm。该振动会增大链条间的拉力，同时也会增大链条与链轮之间的作用力，影响链轮与链条的耐久性，同时也会对液压系统的稳定性造成影响。

(3) 第3阶振型分别作用在内臂、中臂与外臂上，表现为各个臂在XOZ平面上的扭转，最大位移主要集中在外臂的末端与中臂的中间部分，为8.15 mm，但扭转发生的位置集中在外臂与中臂的中间部分。该振动会影响各臂连接处的销轴，对其耐久性产生影响，同时也会对各个臂本身的结构造成破坏。

(4) 第4阶振型主要作用在外臂上，表现为沿Y轴方向上的扭转，最大位移在外臂末端处,为16.16 mm，但扭转主要集中在外臂的中间部分，最大位移为10.78 mm，该振动会对外臂本身结构造成影响。

(5) 第5阶振型主要作用在中臂上，表现为沿Y轴方向上的扭转，最大位移产生在中臂中间位置处，为10.28 mm，该振动会对中臂本身结构造成破坏。

(6) 第6阶振型与第3阶振型相似，主要集中在外臂与中臂上，表现为在XOZ平面上的扭转，扭转的位置也集中在中臂与外臂的中间部分，但中臂扭转的方向与第3阶相反，外臂中间部分扭转的最大位移为9.20 mm，整体最大位移在外臂末端位置，为13.81 mm，该振动会对内臂与外臂本身的结构造成影响。

5 小结

利用SolidWorks对可伸缩式清仓机构进行了三维建模，并对其模型进行了适当的简化处理，取其1/4对称部分导入ANSYS-Workbench中并做出相应的对称平面，对可伸缩式清仓机构进行约束模态分析，得出其前6阶固有频率与振型。所得结论对可伸缩式清仓机构的结构改进与优化设计提供了理论基础，同时也为其清仓过程的振动频率提供了参考。