数据驱动的故障预测方法研究

李 磊，李晓猛，付一博，焦瑞华

(航空工业西安航空制动科技有限公司，陕西 西安 710048)

随着科学技术的不断发展，航空、航天、通信、电子和化工等多个领域的设备日趋复杂和智能，设备使用环境逐渐苛刻，使用强度不断提高，加重了腐蚀、疲劳等外部作用产生退化的可能性，而设备退化引起的失效问题可能会造成严重的人员损伤和财产损失，近年来设备的安全性保障和智能化管理的需求日趋强烈。为全面监控复杂设备的运行情况以及健康状况，保障高效性与经济行、安全性与可靠性，实现复杂设备的视情维修，故障预测与健康管理(Prognostic and Health Management,PHM)技术应运而生，逐渐成为可靠性领域的热点研究方向[1-3]。PHM技术旨在通过精确预测设备寿命为维修替换、备件订购等管理活动提供科学依据，使得系统在未完全故障阶段就可提前获取系统健康状况，实现系统故障前的主动干预，避免被动非计划性停机，达到降低设备过载荷使用和实现设备智能化管理等目标，故大量的专家与学者[1-4]一致认为故障预测是PHM的基础与核心内容。

1 故障预测技术的内涵

1.1 故障预测的概念

故障预测技术通常采用先进传感器技术，基于机理或数据模型来监测和预测设备的状态。该技术可最大程度地利用传统的故障特征检测技术，并综合先进的算法建模，来获得虚警率几乎为零的精确故障检测和隔离结果[5]。从故障预测技术诞生至今，国内外科研人员给出了各式各样不同的定义，然而其核心大多还是围绕剩余使用寿命(Remaining Useful Life,RUL)展开，具体如表1所示。

表1 故障预测的不同定义

综合各类研究观点，认为故障预测的要点可归纳为故障征兆辨识和剩余寿命预测。

① 故障征兆辨识指设备故障的初始特征被识别出来，与正常运转设备特征参数有差别，但设备此时尚能够满足正常运转。

② 剩余寿命预测是指从发现设备的故障征兆开始到设备最终发生故障截至时的时间，并给出尽可能精确的剩余使用寿命预测。

1.2 故障预测方法分类

现有的故障预测方法有很多种，不同的学者和研究机构对其分类略有不同，具体如表2所示。

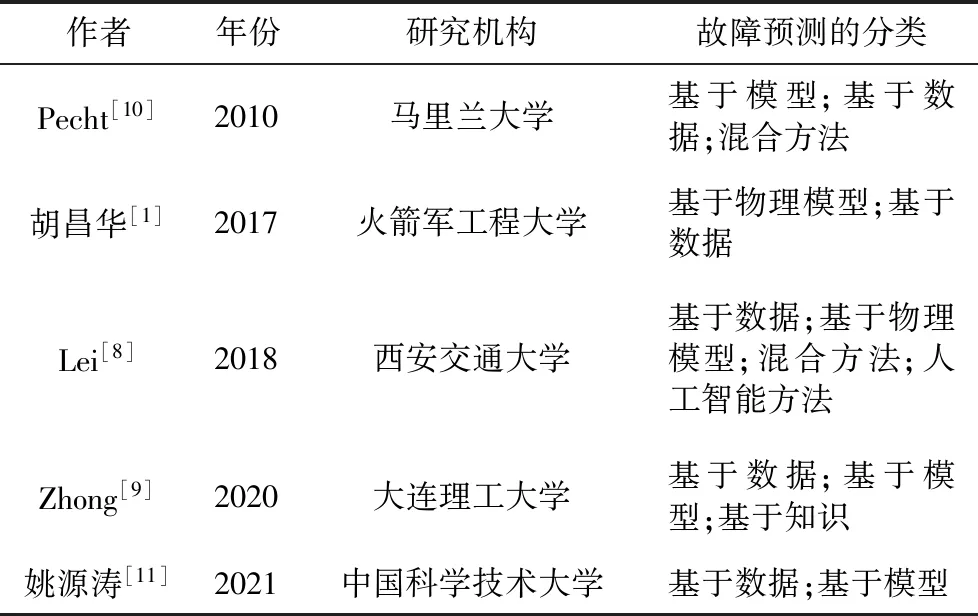
表2 故障预测的分类

结合当前被普遍认同的分类方法，将故障预测方法主要分为基于物理模型的故障预测和基于数据的故障预测。基于物理模型方法的前提是被观测对象的数学模型是已知的，通过建立被观测对象的失效模式和物理特性数学模型，达到识别故障征兆和预测剩余使用寿命的目的。基于数据的故障预测方法以采集到的数据为基础，通过数据分析、处理和提取得到可利用信息，结合历史数据中的输入和输出之间映射关系，完成非线性模型的建立，以期使用现有数据计算未来值，进而实现故障的成功预测。

2 基于数据的故障预测方法

基于模型的故障预测方法虽可以通过研究被观测对象的固有特性和性质，完成对故障的实时预测和精准预测，但是基于模型的故障预测存在建模过程过于复杂的问题，使得其适用范围并不广泛。而基于数据驱动的故障预测方法具备的适用范围广、预测精度高和建模较易等优势使其成为近年来研究的热点与主流，累积了大量的优秀研究成果。因此，下文主要介绍基于数据的几类主流故障预测方法，主要有：时间序列分析方法、可靠性法、随机过程方法和人工智能方法，如图1所示。

图1 基于数据驱动的故障预测方法分类

2.1 时间序列分析方法

该方法将预测对象的历史数据按照时间进行排列，并建立数据随时间变化的数学模型，继而外推至未来进行预测；或将历史数据拟合一条曲线，预测对象随时间变化的趋势，估计出某时刻的预测值。介绍两种故障预测领域常用的时间序列分析方法：灰色模型方法和自回归滑动平均(Auto-Regressive and Moving Average，ARMA)方法。

2.1.1 灰色模型方法

灰色系统模型通常被表示为GM(n,m)，其中n为微分方程的阶数，m为微分方程的变量数。研究人员大多聚焦在计算效率较高的1阶、1个变量的微分方程模型GM(1,1)[12-13]。Yang等[14]建立了一个基于相似信息融合的灰色模型，使用历史样本进行相似性匹配，应用灰色模型预测未来退化轨迹，获取飞机发动机的剩余使用寿命。杜文然等[15]以动车组百万公里故障数据为基础，建立基于灰色GM(1,1)的故障率预测模型，使用等维信息灰色GM(1,1)模型进行数据更新和精度检验，实现对故障的精准预测。灰色模型特点是少数据建模，普遍精度高，误差小[16]。但GM(1,1)模型的预测要求时间序列近似呈指数规律变化，且其只考虑到单个特征量的变化趋势，在实际应用中具有局限性。

2.1.2 自回归滑动平均方法

ARMA方法将数据视为随机序列，结合相邻数据之间的数学关系建立模型，进而拟合时间序列[17]，传统ARMA方法对平稳数据的预测效果良好，适用于短期预测，唐睿[18]使用历史时间序列完成对ARMA模型的建立，得到轴承性能退化的预测曲线，拟合度可以达到96%。徐达等[19]建立ARMA和BP神经网络组合预测模型，以某型装甲装备故障率数据为研究对象，故障率预测结果良好。但是AMRA方法实际运行数据一般较难满足平稳条件，通常需对数据给出平稳性假设或进行合理变换[20]。

2.2 基于可靠性方法

基于可靠性的故障预测方法是从历史数据的统计特性为出发点，使用近似相同的设备历史故障数据来拟合设备的寿命分布曲线，进而获取对应概率密度函数，求得设备平均剩余寿命。所得到的预测结果中含有置信度，能够很好地表征预测结果的准确度。该方法适合用于批次多、数量大的设备[21]。最典型的方法就是比例风险(Proportional Hazards,PH)模型。PH模型中设备的失效率由基准失效率函数和协变量函数组成，在预测结果的同时体现了同类设备的共性属性和个体差异。蒋文博等[22]运用PH模型结合寿命和协变量的关系，获取累计风险函数，利用机器学习算法结合寿命数据和故障时间序列建模，所得到的寿命预测结果良好。但是PH模型需要大量的高可靠历史数据才能完成对模型参数的推算，另外还需要失效率和协变量的差异成比例，使得其在寿命预测领域的应用并不具备广泛适用性[23]。

2.3 基于随机过程方法

该方法旨在通过建立随机过程模型以获取退化过程的曲线，进而得到剩余寿命概率分布函数。主要包括的方法有基于Wiener过程的方法、基于马尔可夫链的方法、基于Gamma 过程的方法和基于逆高斯过程的方法。

2.3.1 基于Wiener过程的方法

Wiener过程又称为带线性漂移的布朗运动，由于其在非单调性能退化方面的良好表现，常被用于非单调退化过程的建模[24-25]，目前已被广泛应用于设备可靠性分析和寿命预测领域。赵帅[26]使用Wiener随机过程分别对设备单调和非单调退化过程进行驱动，引入PH模型到退化过程中并对设备故障预测进行建模，通过转移矩阵的方法完成对模型的解算和设备健康参数的求解，实现对设备故障的准确预测。董青等[27]基于自适应Wiener过程，提出了一种考虑随机冲击影响的非线性退化设备剩余寿命预测方法。利用正态分布描述随机冲击对设备退化量的影响，建立融合随机冲击影响的自适应Wiener过程退化模型，并应用期望最大化方法实现模型参数估计，通过数值仿真、惯性导航系统陀螺仪实例，验证了方法的有效性和实用性。但Wiener存在过程参数的辨识需要大量的历史数据和不适用于非线性退化建模的缺陷。

2.3.2 基于马尔可夫链的方法

该方法在故障预测领域，首先需假设退化过程{X(t),t≥0}在有限的状态空间E={0,1,2,…,M}上进行演化迭代，被观测对象首次达到失效状态点“M”的时间为设备的使用寿命。这种方法具备似然函数计算效率高和简单直观的优点，但当被观测对象退化过程难以获取时，隐马尔可夫模型(Hidden Markov Model，HMM)得到了广泛的应用，其结构示意图如图2所示。

图2 HMM的结构示意图

HMM 模型是由两个随机过程生成，一个随机过程用于描述可观测状态的转移，另一个用于状态与观测值之间的映射关系。转移过程通常是随机的，其状态对应的观测也为随机，所以只能通过其一随机过程估计状态的存在和其特性。另外，HMM模型在故障预测应用中还将被观测对象的健康状况划分为“健康”、“亚健康”、“失效”等便于理解的描述方式。杨奕飞等[28]研究了基于隐马尔科夫模型的故障模式识别方法,利用该模型将微弱变化的信号特征转换为变化较大的对数似然概率对故障模式实现有效识别。周智利[29]提出一种基于HMM模型的转辙机故障及剩余寿命预测方法，通过实验获取到的被观测设备的故障预测结果较为良好。由于该方法的无记忆性，造成寿命预测结果仅依赖当前设备的健康状态而不能充分利用设备运行过程的历史数据。另外，该方法无法得到概率密度函数，进而无法对故障预测结果进行评估。其近似离散化的处理连续退化过程的方法也会存在误差。

2.3.3 基于Gamma 过程的方法

基于 Gamma 过程的故障预测方法需要假设设备的退化模型的增量服从Gamma 分布，在预先设定好失效阈值的前提下求取失效阈值的时间就可以得到剩余寿命[30]。Gamma 随机过程为一种单调递增的跳跃过程，可用于设备随机退化过程为严格单调的情况。高首[31]建立了基于 Gamma过程的模型描述产品的退化过程，针对激光器和锂离子电池退化模型，创新地应用了粒子滤波算法对EM 算法中不易估计的参数值进行求解，并最终得到了相应的剩余寿命概率密度函数。李建华[32]建立了一种基于二元伽马过程的退化模型，利用分步极大似然估计法在线更新模型参数并对设备的剩余寿命进行预测，预测精度良好。但受限于实际退化过程的无序波动性，现实退化场景往往并不严格遵循Gamma随机过程的单调特性。另外，Gamma分布数学形式较为复杂，存在难以对模型的参数进行实时估计和更新的问题。

2.3.4 基于逆高斯过程的方法

与Gamma过程相似，逆高斯过程是一种具有单调性的随机过程。其在实际应用中能够较为方便地融入其他物理模型，在设备的可靠性评估工作中具有较为广泛的应用前景[33-34]。王艺斐等[35]采用二元过程建立管道剩余强度性能退化量模型，基于管道剩余强度的边缘概率密度函数，采用期望值最大化算法估计模型参数，完成管道寿命预测。吴振宇[36]基于逆高斯过程提出一种考虑个体差异和测量不确定性的加速退化模型，通过遗传算法和蒙特卡洛积分的方法对模型参数进行求解，实现了设备的寿命预测。目前关于逆高斯过程在寿命预测中的研究相对较少，且逆高斯过程适用于退化过程单调的应用场景，在复杂退化过程的应用研究较为缺乏。

2.4 基于人工智能的方法

基于人工智能的方法首先选取若干历史数据作为训练样本，再使用训练算法对其训练后进行故障预测。该方法避免了传统方法较为复杂的数学模型建立和专家经验获取。但需要被观测对象从起始使用到最终故障时的完整历史数据，否则会降低预测结果的可信度。另外，由于这类方法属于黑盒模型，这也意味着预测结果往往缺乏足够的可解释性。目前常用的人工智能方法有：人工神经网络(Artificial Neural Network,ANN)、支持向量机(Support Vector Machine,SVM)和深度学习等方法。

2.4.1 基于ANN的方法

常见ANN有BP网络、SOM网络、RBF网络等。故障预测中最常用的BP神经网络是一种单向传播的多层前向网络，其结构如图3所示。

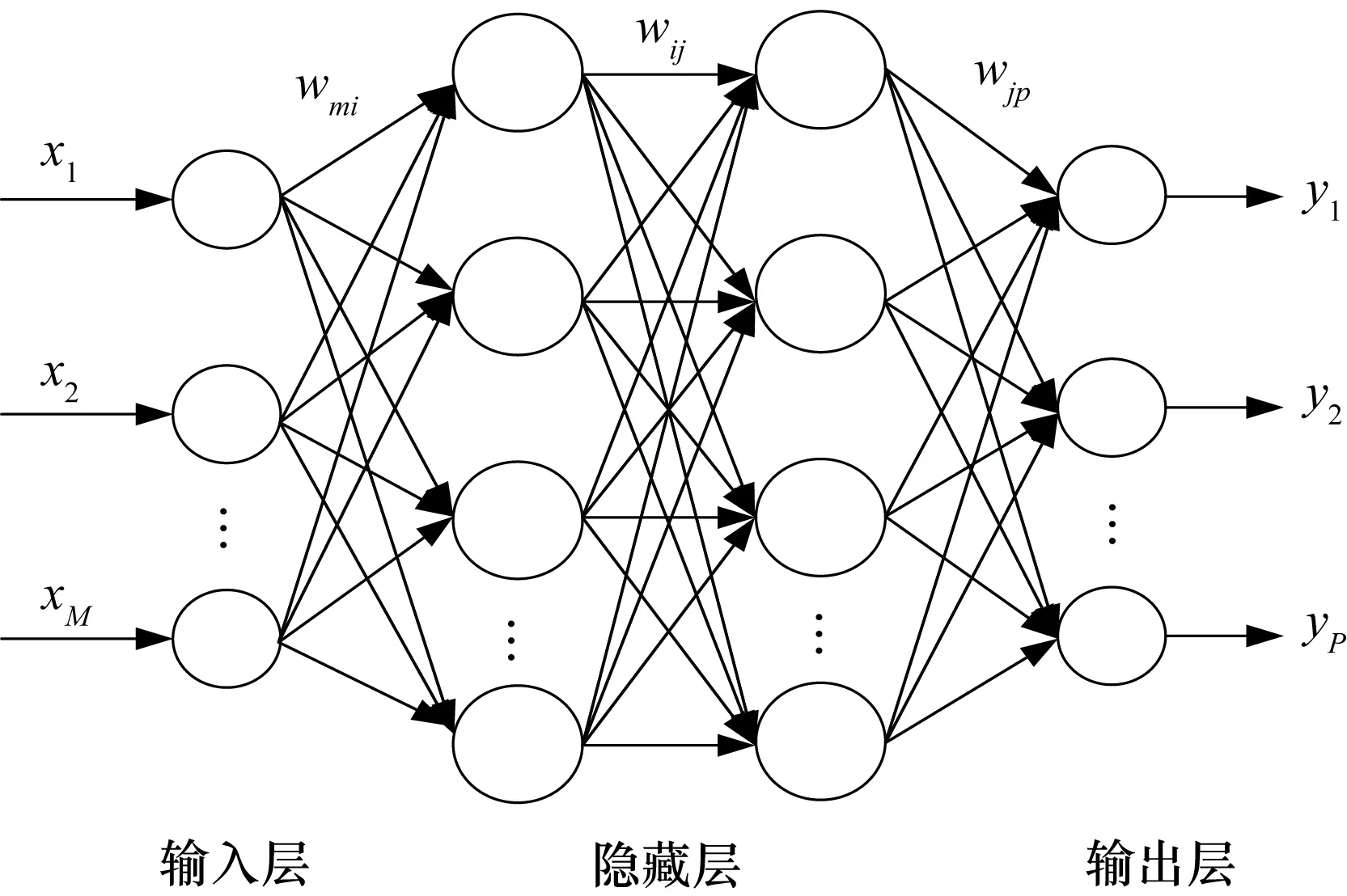
图3 BP神经网络结构

输入信号从输入节点依次穿过各隐藏层节点，然后传到输出节点，节点传递函数一般为sigmoid型函数。BP神经网络从输入节点到输出节点存在某一映射g的最佳逼近，通过多次反复拟合训练，最终得以近似复杂函数。隐藏层个数的选取根据经验公式或者采取试算的方法，输出层只选取一个，即预测的寿命值。神经网络能较好地反映出设备状态信号与性能退化趋势之间的关系，适合非线性复杂系统的故障预测。苏续军等[37]对利用无人机系统故障数据集预测无人机故障时的相关问题进行分析,给出BP神经网络的建模思路和计算方法，使用特征变量显著性筛选技术识别故障影响因素,有效地应用至无人机故障预测中。赵辉[38]在对齿轮箱的轴承温度进行预测时，使用了BP神经网络算法，所得实验结果良好，平均误差能够控制在5%以内。但ANN方法同时也存在诸多问题，如网络训练时间长、易陷入局部最优点、隐含层数与节点选取困难和需要大量数据为依据等。

2.4.2 基于SVM的方法

基于SVM的故障预测方法是基于统计学习理论的结构风险最小化原则的方法。SVM方法的原理旨在求解能够正确划分训练数据集并且几何间隔最大的分离超平面。如图4所示，wx+b=0即为分离超平面，找到最大间隔超平面对数据进行分类。

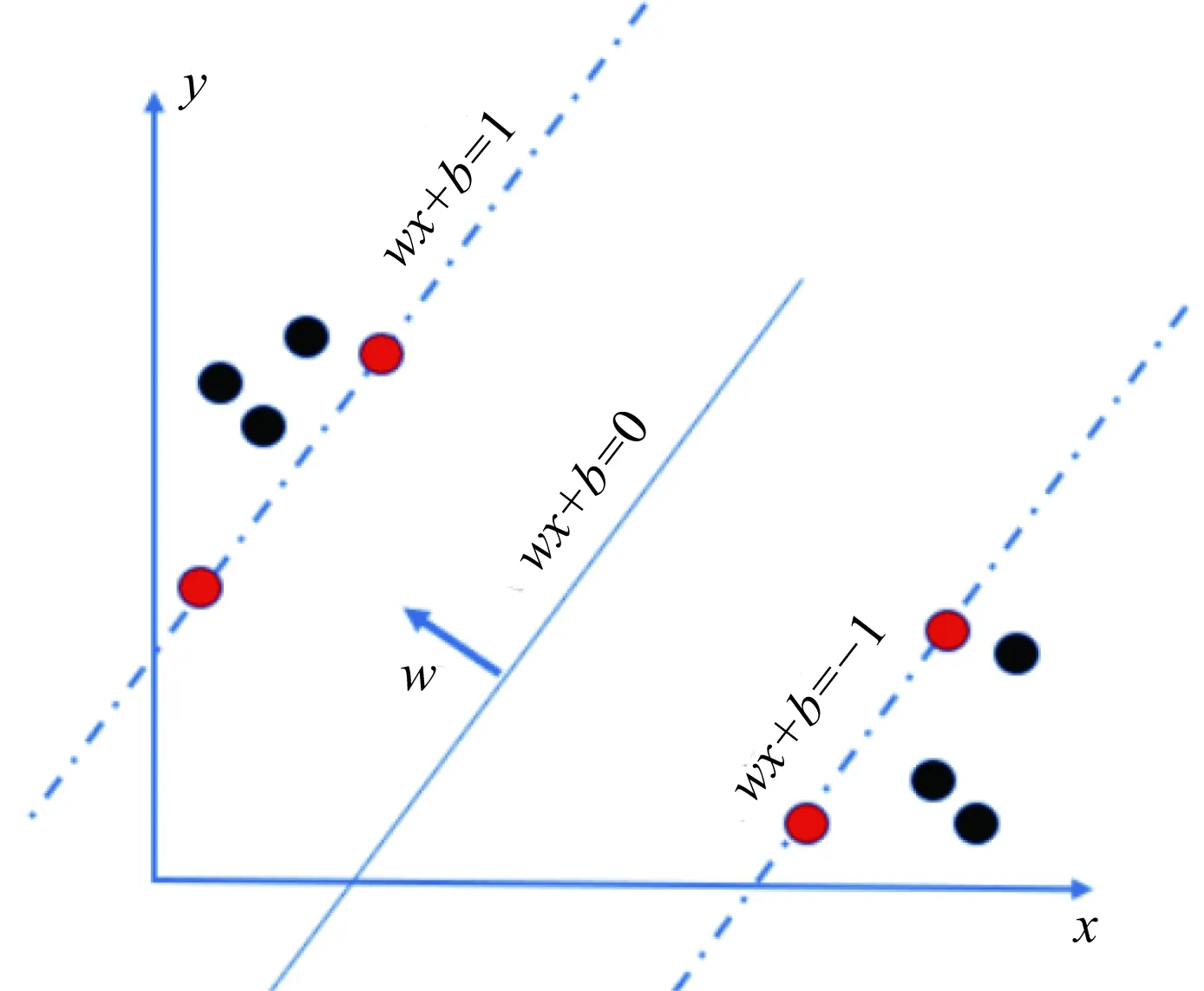
图4 SVM原理图

同传统人工智能方法不同，SVM方法可以用于历史故障数据较少的情况，因此，基于SVM的故障预测方法近年得到越来越多业界学者关注。目前已有多个不同类型的SVM方法应用在设备故障预测中，如One-Class SVM 、Least Square-SVM and Multi-Class SVM等方法。王伊婧心等[39]利用经验模态分解理论与最小二乘支持向量机构建了一种新的预测模型，对非平稳时间序列进行EMD分解，通过改进高斯核函数提高其泛化能力，并利用改进的LS-SVM对各分量进行训练及预测，通过对波音飞机的经典故障率预测算例,验证方法的有效性和优越性。另外，支持向量回归方法是SVM在故障预测中的应用形式，Benkedjouh等[40]使用该方法建立磨损特征和磨损程度之间的非线性关系，并应用于磨损机器的剩余寿命预测中。SVM也存在诸多局限性，其最主要的问题在于不能够提供概率预测，进而增加了预测结果获取的不确定性。

2.4.3 基于深度学习的方法

深度学习旨在通过模拟大脑的学习过程，结合海量的训练数据，对更高阶的本质特征进行信息提取，并逐层进化特征传递，实现信息的认知计算。深度学习通过建立深层次模型克服了传统方法模型学习能力及泛化性能不足的问题，被广泛应用于设备的剩余寿命预测，其主要的网络模型有卷积神经网络(Convolutional Neural Network，CNN)、长短期记忆网络(Long Short-Term Memory，LSTM)和深度置信网络(Deep Belief Network，DBN)。

CNN是典型的深度前馈人工神经网络,受到生物学感受机制的启发，一般由卷积层、池化层和全连接层等组成，其主要优势有：① 共享权值，可很大程度地降低参数数量；② 局部连接，可以有效提升计算速度，减少参数数量；③ 下采用，可减少样本总数，使得模型在具有鲁棒性的同时减少参数数量[41]。这些优势使得CNN可以最大程度地进行事物的特征提取，使其具备强大的认知和计算能力,为此学者们开始将其引入到故障预测领域,取得了不错的效果。Alqasem等[42]使用CNN方法用于软件故障预测研究，通过使用NASA的4个常用数据集(即PC1、KC1、KC2和CM1)进行试验，CNN的准确率和检出率分别达到标准值：PC1 97.7%、73.9%，KC1 100%、100%，KC2 99.3%、99.2%，CM1 97.3%、82.3%。王文庆等[43]利用CNN自动提取传感器数据的局部抽象特征，采用具有长短期记忆能力的GRU来记忆序列的前后关系，提高RUL的预测精度，使用CNN进行自动滤波，显著提升了预测值的稳定性和准确度。

LSTM网络的优势在于可以应用于较长时间序列的预测，具有较长时间的记忆功能，同时LSTM可以有效地解决训练过程中出现的梯度爆炸和梯度消失问题[44]。LTSM的这些优势能够有效地挖掘数据的内在结构信息和关联性,使得故障预测建模精度得以提高。何群等[45]利用相关输入变量之间重要关联信息,对历史监测数据进行训练学习,建立齿轮箱油温监测LSTM模型,对预测残差进行评估计算设定相应的检测阈值,通过模型残差分析和阈值比较实现齿轮箱故障状态的检测和预测，结果表明，该方法表现出更好的预测性能,能够较早预测故障的发生。Liu等[46]将LSTM模型与统计过程分析相结合，使用NASA和FEMTO-ST研究所发布的轴承数据集进行实验，预测航空发动机轴承多阶段性能退化的故障，结果表明该方法具有更高的预测精度。

DBN方法依托于无监督深度学习模型，使用受限玻尔兹曼机(Restricted Boltzmann Machin，RBM)对原始数据的特征进行自动化提取。DBN模型的特征提取能力较强，能够克服被观测设备内部器件的机理和数据差异，使用从内部各器件所得到的数据可直接进行预测数学模型的建立。代杰杰等[47]使用国家电网公司收集的实际变压器数据，采用DBN建立变压器运行模型，并融合LSTM预测变压器油中未来特征气体浓度和变压器状态。结果表明，该方法具有较高的预测精度，能够分析潜在故障。梁天辰[48]基于历史数据和实时数据对多个DBN模型进行迁移训练，有效解决历史域和目标域数据分布差异带来的预测偏差。

3 结束语

介绍了故障预测技术的相关理论概念和内涵，对当前设备广泛应用的基于数据驱动的故障预测技术进行了调研和分析，重点介绍了数据驱动方法中的时间序列分析法、可靠性法、随机过程方法和人工智能方法，详细论述了各类方法的优点和不足，并给出各类方法在国内外的最新研究进展。虽然现有研究成果在故障预测领域已取得一些阶段性的成果，但还存在许多问题，有待进一步深入研究和解决。

① 层级信息互耦合的复杂系统精准故障预测。实际被观测对象往往由多个互关联和互耦合的子部件或者子系统组成。但目前大多研究成果主要集中在单一层级部件的故障预测上，如Peng[49]和Li[50]等都是针对航空发动机系统层级的研究，缺乏对融合多层级互耦合信息的部件进行故障预测研究。因此，需研究建立子部件级、子系统级和总体系统级的多层次一体化监控预测体系，融合各层级互耦合信息，进而完成对复杂系统的系统级精准故障预测。

② 动态运行环境下的复杂系统精确故障预测。在实际工程应用过程中，被测对象所处环境通常是动态变化而非一成不变，退化过程也会因所处复杂环境的动态变化而发生改变。因此，在进行复杂系统故障预测时必须考虑现场复杂环境的变化。而部分涉及动态运行环境分析的研究，普遍缺乏对故障模型的普适性，如王振伟等[51]对半球谐振陀螺的故障模式进行在线动态检测，存在缓发性故障检测能力不足等问题。所以，在退化建模过程中，需研究新的方法模拟环境动态变化全过程并将其引入到构建的退化模型之中，使得退化建模更加接近实际现场退化过程，进而提高故障预测的精度。

③ 子部件动态变换下的复杂系统级精确故障预测。实际系统的运行往往伴随子部件的维护和更换的情况，这种情况会导致故障预测模型变换，预测结果也会从非健康状态突变至亚健康状态或健康状态。因此，开展考虑子部件变换情况下复杂系统故障预测的研究工作势在必行。虽然已有诸多学者试图解决这种问题，如郑建飞等[52]提出的不完全维护影响的退化建模和RUL预测方法，但在状态残余量的估计准确性和非新维护的RUL预测的准确性上存在诸多不足。需要研究基于设备的随机退化模型与子部件动态变换模型来构建新的综合退化模型，使用新的估计模型参数方法。

④ 深度网络模型在线状态情况下的复杂系统精确故障预测。现有深度网络模型研究成果大多使用离线过程分析，如Ellefsen等[53]通过对深度网络模型的建立，研究了半监督模式下的深度学习方法在离线故障预测方面的应用。另外，多数深度网络模型存在训练时间较长，模型可解释性较差，模型参数缺乏统一选取标准等问题。因此，需研究确定模型参数的选取标准，并在此基础上，研究设计具备模型可解释功能的短训练深度网络模型。

⑤ 基于不完美数据的复杂系统故障预测。基于数据驱动的故障预测方法本质上是将试验获取数据与预测模型相结合的方法，而在实际工程应用过程中，由于设备运行环境的复杂多变和设备本身的客观不确定性，所获取的试验数据很可能存在数据量少、噪声干扰、数据抖动、数据缺失等问题，这些不完美数据会对预测结果带来影响。最新研究成果显示已有学者提出一些解决方案，但大多都是针对单一特定数据问题，如张晟斐等[54]提出针对缺失数据下的剩余寿命预测方法和张旺等[55]提出针对数据噪声干扰下的剩余寿命预测方法。因此，需要通过研究探索扩展数据或者数据融合等新方法保证数据质量，进而提升不完美数据状况下的故障预测精度。