弱C轴择优AlN薄膜晶体测温技术研究

董 玲，李 杨，吕静雯，蒋洪川，张万里

(1.电子科技大学 电子薄膜与集成器件国家重点实验室，四川 成都 611731；2.西北工业大学 动力与能源学院，陕西 西安 710129)

为了提高航空发动机推重比，其压缩机压缩比、转速及涡轮前温度都相应提高，因此转子承受着更大的热负荷。涡轮叶片承受的热负荷是叶片烧蚀、断裂的重要因素之一，准确测量涡轮叶片的表面温度并掌握其温度分布规律是分析涡轮叶片烧蚀断裂等故障诊断的重要依据。

航空发动机涡轮叶片表面温度测量方法主要有：热电偶测温[1-2]、辐照晶体测温[3-5]、示温漆测温[6-7]、红外辐射测温[8-9]等。薄膜热电偶技术具有薄膜化、集成化、不干扰流场等优势，但还存在测试引线难、附着力不高、稳定性较低等问题。辐照晶体测温是一种非在线测温技术，其无需引线、测温精度高，可进行高密度阵列式布点，测试改装易实现，但工艺复杂、成本高昂。示温漆测温技术具有无需引线、不会破坏被测件结构、不破坏流场、附着力高等优势，但其测试精度低。红外辐射测温技术对于高速旋转物体、运动物体的测温具有绝对优势，但被测试件的发射率变化会给测试结果带来较大误差，并且探头的安装位置、冷却方式也极大地限制了红外测温技术的应用。就上述几种测温方式而言，辐照晶体测温尤其适用于缘板、榫头等结构复杂位置的温度测量。根据本课题组前期对SiC辐照晶体测温技术的研究可知，晶体测温工艺复杂，成本高昂。基于晶体测温技术，本文提出薄膜晶体测温技术，以实现降低测温操作难度、降低测温成本的目的。

AlN 薄膜材料具有耐高温、导热性良好、热膨胀系数小、耐热冲击、绝缘等优良性能，使得它在航空航天领域具有潜在的应用价值。闫帅[10]研究发现，AlN 薄膜 (002)晶面衍射峰峰位随退火温度的升高和退火时间的累积而线性增大，因此，可以利用AlN 薄膜的晶格参数与退火温度的关系进行温度测量。相较于 SiC 晶体测温技术，AlN薄膜晶体测温同样是一种非在线测温技术，但其不需要昂贵的高剂量中子辐照技术，不需要成品率低的切片工艺，也不需要在涡轮叶片表面开孔填埋的复杂工艺，只需采用薄膜技术在涡轮叶片表面沉积弱 C 轴择优的 AlN 陶瓷薄膜，因此，其易实现叶片表面温度的多点测量。本文系统地研究了退火对弱 C 轴择优 AlN 薄膜缺陷的修复情况，并利用退火温度、退火时间和 (002)晶面衍射峰 2θ值的相关数据建立温度判读算法，再采用 MATLAB 编写温度判读软件，实现了温度的可视化判读。

1 实验

采用 JPG560 磁控溅射系统在 Al2O3陶瓷片上沉积弱 C 轴择优 AlN 薄膜，溅射使用靶材为 250 mm×100 mm×10 mm 的矩形铝靶(纯度大于99.99%)，工作气体为高纯 Ar 与高纯N2(纯度大于99.99%)。溅射之前，首先用丙酮、乙醇和去离子水分别对 Al2O3陶瓷片超声清洗10 min，并用氮气枪吹干备用；然后，将基板加热至300 ℃；向溅射腔通入纯氩气，预溅射5 min；接着将工作气体换为纯氮气，调节工作气压为0.8 Pa，溅射功率为2000 W，进行 AlN 薄膜的沉积，溅射时间为1.5 h，薄膜厚度大约为2.5 μm。

对沉积的 AlN 薄膜样品进行真空退火处理，管式炉真空度大约为0.6 Pa，退火温度分别为400 ℃、500 ℃、600 ℃、700 ℃、800 ℃、900 ℃、1000 ℃，退火时间为40 min，重复退火两次。采用 Ultima Ⅳ X射线衍射仪(CuKα,40 kV,40 mA)表征薄膜的晶体结构，测试角度为30°～50°，步长为0.02°，扫描速率为6°/min。利用 MATLAB 软件线性拟合2θ、退火温度和退火时间，建立温度判读算法，并基于温度判读算法编写温度判读软件。

2 结果与讨论

2.1 AlN薄膜的结构分析

AlN 薄膜的 X 射线衍射图如图1所示，在衍射角30°～50°范围内，只出现了 (002)衍射峰，表明 AlN 薄膜为 C 轴择优生长。图2为 AlN 薄膜的摇摆曲线，该摇摆曲线的半峰宽较宽，表明薄膜为弱C 轴择优取向。弱 C 轴择优取向相较于高度择优取向的 AlN 薄膜，其内部具有更多缺陷[11]。采用 Jade 数据处理软件识别出薄膜 (002)衍射角 2θ值为35.994°，由六方纤锌矿结构的 AlN 标准卡片PDF#25-1133可知 (002)衍射峰的标准峰位为36.04°。由此可见，该工艺条件下制备的 AlN 薄膜 (002)衍射峰发生了严重的左移，根据布拉格方程[12]2dsinθ=kλ可以推出薄膜的晶格间距d增大，表明该工艺条件下制备的薄膜晶格膨胀较为严重。引起薄膜出现较大晶格膨胀的原因可能与工作气体相关。由于采用了纯氮气作为工作气体，氮气被电离成N5+和N3-，N5+所带电荷数较多，因此经电场加速之后具有较大的动能，进而导致溅射产额较大，并且溅射出的粒子能量较高，最终导致薄膜晶格膨胀较为严重。本文采用退火的方式来降低薄膜晶格膨胀，并研究了退火温度、退火时间与薄膜晶格结构变化的关系。

图1 AlN薄膜的X射线衍射图

图2 AlN薄膜的摇摆曲线

图 3为 AlN 薄膜退火之后的X射线衍射图，由图3可知，AlN 薄膜经过退火处理之后，其 (002)衍射峰发生了明显的右移。表1为两次退火之后，AlN薄膜 (002)晶面衍射峰的 2θ值，由表1可以看出薄膜的 2θ值随退火温度的升高而近似线性增大，并且随着退火时间的累积也逐渐增大。但退火温度达到1000 ℃，第二次退火40 min后，薄膜的 2θ值反而减小。可以推测在不同的温度环境下，薄膜中的缺陷在不断的湮灭与产生，当退火温度达到1000 ℃时，薄膜中缺陷的产生速度大于缺陷湮灭的速度，因此薄膜的 2θ值反而降低。基于 AlN 薄膜 (002)晶面衍射峰的 2θ值与退火温度和退火时间的线性关系，可以建立温度判读算法，为热端部件表面的温度测量提供依据。

图3 AlN薄膜退火之后的X射线衍射图

表1 不同退火温度及不同退火时间条件下的2θ值

由XRD分析结果可知，退火可以逐步修复弱C轴择优取向AlN薄膜的晶格缺陷，从而使晶格膨胀减弱。而晶格缺陷的变化又可以用衍射角2θ的变化来表示，因此依据测量薄膜晶格参数2θ值即可反演出薄膜经历的最高温度。

2.2 温度判读算法的建立

将退火温度、退火时间和对应的 2θ值输入 MATLAB 软件生成矩阵数列，再利用 MATLAB 的Curve Fitting功能模块对矩阵数列进行线性拟合得到温度判读算法公式，如式(1)所示。同时采用文献[11]中报道的温度判读算法公式(2)对矩阵数列进行拟合，并对两种温度判读算法进行比较，根据线性相关系数、方差和标准差的差距，优选出较好的温度判读算法。

2θ=A+B×t+C×T

(1)

2θ=a+b×t+c×log10T

(2)

式中:2θ为 AlN 薄膜 (002)晶面衍射角;t为退火时间;T为退火温度;A、B、C为常数；a、b、c也为常数。

主要应用数值拟合计算常数A、B、C和常数a、b、c。首先将多组退火样品的测试数据(包括退火时间、退火温度和对应的2θ值)分别赋予X,Y,Z矩阵形式，如式(3)～式(5)所示。

X=[t1,t2,t2，…，tn]

(3)

Y=[T1,T2,T3，…，Tn]

(4)

Z=[2θ1,2θ2,2θ3，…，2θn]

(5)

然后进入 MATLAB 的Curve Fitting Tool 进行拟合条件的设置。设置项主要为拟合方式的选择，式(1)是采用多项式(polynomial)拟合方式，而式(2)是采用自定义方程拟合得到的。拟合过程相当于求三元一次方程组(X,Y,Z)的解，最后得到所需的3个常数变量。式(1)中常数A、B、C的拟合结果分别为35.97、2.583×10-4、6.543×10-5，而式(2)中常数a、b、c的拟合结果分别为35.76、2.583×10-4、0.09151。

不同的温度判读算法拟合结果如图4所示，包括拟合出的曲面图以及对应的残差图。

两种温度判读算法的线性相关系数平方(R2)，标准差(RMSE)和残差平方和(SSE)如表2所示。其中线性相关系数越接近1表明变量之间的相关性越强，RMSE越小则预测值与真实值之间的偏差越小，SSE越小表明每个样本各观测值越收敛。对比之下，可以优选式(1)作为温度判读算法。

表2 两种温度判读算法的R2、RMSE和SSE

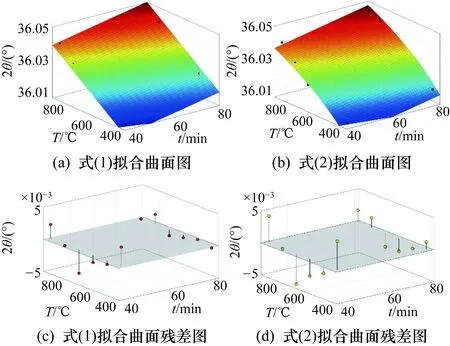
图4 不同的温度判读算法拟合结果

2.3 温度判读软件的建立

在 MATLAB的命令窗口输入guide调出图形用户设计界面，添加axse、text、edit、pushbutton等对象。针对单个对象，选中查看回调选项，在其 callback 回调函数下编写相应的指令代码。完成代码编写之后，运行该温度判读程序可以出现如图5所示的温度判读界面，输入常数A、B、C的值，点击 2θ标定曲线按钮即可得到 2θ标定曲线图。针对温度判读样品而言，只需输入退火时间与晶格参数 2θ即可判读样品经历的最高温度T。

图5 温度判读界面图

将退火时间(40 min,80 min)和样品的 2θ值输入温度判读软件，可以得到判读温度，如表3所示。由温度判读误差可以看出，除个别温度点判读误差较大以外，温度判读误差基本可以控制在7%以内，并且高温段的温度判读误差更低。

表3 温度判读数据及误差

上述对弱C轴择优取向AlN薄膜的研究尚处于实验阶段。在实际工程应用中，测温晶体随涡轮叶片等高温部件一起经历高温再冷却至室温，可以得到涡轮叶片转速与时间的历程曲线图，并可以测得薄膜的衍射角2θ。要计算薄膜晶体经历的最高温度还需要引入一个关键的变量，即等效时间teqv。等效时间被定义为实际多个温度段导致薄膜晶体发生晶格变化所需的时间等效为最高温度下产生相同晶格变化所需的时间。由于实验阶段采用了快速升降温的方式，因此，退火时间即可以被认为是等效时间。以本课题组前期进行的 SiC 晶体测温技术为例[13]，实际工程中，要计算等效时间，首先需要将涡轮叶片转速-时间历程曲线图进行归一化处理，再将其等效处理为温度-时间历程曲线图，如图6所示。

图6 温度-时间历程曲线

再采用迭代计算的方法可以得出等效时间，同时也可以计算出最高温度，图7为等效时间迭代计算图。首先，假设当温度达到最高温度时，晶体才发生晶格变化，则可以得到最高温度下的等效时间teqv100，将测量的2θ值和等效时间teqv100代入算法公式，可以计算出一个最高温度T100。但实际上，当温度达到某一临界值时，晶格就已经开始变化。又假设这个临界温度是T100×90%，因此可以将该温度和2θ值代入算法公式进行迭代，得到新的等效时间teqv90。此时引入时间等价系数K=teqv90/teqv100，那么就可以进一步求出更接近真实值的等效时间t1，再将等效时间t1与2θ值代入算法公式可以得到最高温度T1。通过对临近两次计算出的最高温度进行判别，设置判读误差，如果两次判读结果在误差范围内，则输出最高温度与等效时间。

图7 等效时间迭代计算图

等效时间的迭代过程即为温度的判读过程，利用该判读技术可以实现温度的可视化判读。本研究后续将对 AlN 薄膜晶体测温技术作进一步研究，努力做到工程应用，它对我国航空航天高温部件表面温度的准确测量具有十分重大的意义。

3 结束语

采用中频反应磁控溅射法制备了具有弱 C 轴择优取向的 AlN 薄膜。对 AlN 薄膜进行了真空退火处理，薄膜的 2θ值随退火温度的升高和退火时间的累积而线性增大，利用 MATLAB 软件对 AlN 薄膜的晶格参数 2θ与退火温度和退火时间进行线性拟合得到温度判读算法公式。借助 MATLAB 的 GUI 模块实现可视化温度判读，在400～1000 ℃范围内，温度判读误差可以控制在7%以内。薄膜晶体测温技术将大力推动晶体测温技术发展，大幅降低晶体测温技术的难度和成本，对航空发动机特殊位置的温度测量具有重要意义。