Constraining Brans-Dicke Cosmology with the CSST Galaxy Clustering Spectroscopic Survey

Anda Chen ,Yan Gong ,Fengquan Wu ,Yougang Wang ,and Xuelei Chen2,,5

1 Key Laboratory of Space Astronomy and Technology,National Astronomical Observatories,Chinese Academy of Sciences,Beijing 100101,China gongyan@bao.ac.cn

2 School of Astronomy and Space Sciences,University of Chinese Academy of Sciences,Beijing 100049,China

3 Science Center for China Space Station Telescope,National Astronomical Observatories,Chinese Academy of Sciences,Beijing 100101,China

4 Key Laboratory of Computational Astrophysics,National Astronomical Observatories,Chinese Academy of Sciences,Beijing 100101,China

5 Center for High Energy Physics,Peking University,Beijing 100871,China

Abstract The Brans–Dicke (BD) theory is the simplest Scalar-Tensor theory of gravity,which can be considered as a candidate of modified Einstein’s theory of general relativity.In this work,we forecast the constraints on BD theory in the CSST galaxy clustering spectroscopic survey with a magnitude limit～23 AB mag for point-source 5σ detection.We generate mock data based on the zCOSMOS catalog and consider the observational and instrumental effects of the CSST spectroscopic survey.We predict galaxy power spectra in the BD theory from z=0 to 1.5,and the galaxy bias and other systematical parameters are also included.The Markov Chain Monte Carlo technique is employed to find the best-fits and probability distributions of the cosmological and systematical parameters.A BD parameter ζ is introduced,which satisfiesWe find that the CSST spectroscopic galaxy clustering survey can give |ζ|＜10-2,or equivalently under the assumption ζ=0.These constraints are almost at the same order of magnitude compared to the joint constraints using the current cosmic microwave background,baryon acoustic oscillations and Type Ia supernova data,indicating that the CSST galaxy clustering spectroscopic survey would be powerful for constraining the BD theory and other modified gravity theories.

Key words:cosmology– cosmological models– cosmological parameters from large-scale structure

1.Introduction

The cosmic acceleration,which is discovered in 1998(Riess et al.1998;Perlmutter et al.1999),is a great mystery of modern cosmology.To explain this phenomenon,different kinds of dark energy (DE) models have been considered,including the cosmological constant (CC) in the standard Λ CDM model.The mechanism of cosmic acceleration cannot be explained in the gravitational theory frame including only general relativity(GR)without DE,and that can also be seen as the incompleteness of GR.Thus,another alternative physical explanation is modified gravity (MD),i.e.,the modification of Einstein’s GR theory.Generally,the main difference between MD and DE is whether a theory violates the strong equivalence principle (SEP) or not.In other words,a DE model must obey the SEP,and an MD model does not comply with it (for more details,see,e.g.,Joyce et al.2016).The Jordan–Fierz–Brans–Dicke theory(Brans&Dicke 1961;Dicke 1962,for a historical perspective,see Brans(2014),hereafter we call it Brans–Dicke(BD) theory for simplicity) is a typical example of a modified scenario to GR.The BD theory is based on Mach’s Principle,and it is the simplest case of the scalar-tensor theory of gravity and a natural alternative to GR.

For decades,the astrophysical and astronomical observations have supplied various constraints on the BD parameter ω.According to solar system data obtained from the Cassini-Huygens mission,the estimation of ω is given as ω ＞40,000 at the 2σ (95.5%) confidence level (CL) (Bertotti et al.2003;Will 2006;Perivolaropoulos 2010).For modifying the evolution of our universe,some cosmological methods can also be used to test the BD theory.There are several different cosmological approaches,such as cosmic microwave background(CMB),galaxy clustering and Type Ia supernovae(SNe Ia).By using the combined CMB data and cosmic large-scale structure (LSS) measurements,including Wilkinson Microwave Anisotropy Probe(WMAP)five-year data,the Arcminute Cosmology Bolometer Array Receiver (ACBAR) 2007 data,the Cosmic Background Imager (CBI) polarization data,the Balloon Observations Of Millimetric Extragalactic Radiation and Geophysics (BOOMERanG) 2003 flight data and the luminous red galaxy (LRG) survey of the Sloan Digital Sky Survey (SDSS) Data Release 4 (DR4),Wu &Chen (2010)found ω ＞97.8 or ω ＜-120.0 at 2σ CL.By using CMB data from WMAP,ACBAR,VSA,CBI and galaxy power spectrum data from 2dF Galaxy Redshift Survey,Acquaviva et al.(2005)obtained ω ＞120.0 at 2σ CL.Based on the CMB temperature data from the Planck satellite and the nine-year polarization data from WMAP,and baryon acoustic oscillations (BAO)distance ratio data from SDSS,Li et al.(2013) excluded the region of ω value in -407.0 ＜ω ＜175.87.Besides,using the combined data sets of CMB,BAO and SN Ia,Li et al.(2015)excluded the region of -9999.50 ＜ω ＜232.06.

Since the LSS formation and evolution are tightly related to the properties of gravity,the BD theory and other MD theories can be constrained by LSS related observations,such as BAO(see e.g.,Eisenstein 2005),weak gravitational lensing (WL;e.g.,Kaiser 1992,1998 and redshift-space distortion (RSD;Jackson 1972;Kaiser 1987).Some ongoing and planned telescopes are devoted to perform relevant measurements,e.g.,SDSS (Fukugita et al.1996;York et al.2000),the Large Synoptic Survey Telescope (LSST,Ivezic et al.2008;Abell et al.2009) and Euclid Space Telescope (Laureijs et al.2011).The China Space Station Telescope(CSST)(Zhan 2011,2018;Cao et al.2018;Gong et al.2019) is also this kind of project.The CSST,which is planned to launch around 2024,is a 2 m space telescope and in the same orbit with the China Manned Space Station.The telescope can carry out both photometric imaging and slitless-grating spectroscopic surveys simultaneously.The survey will cover a 17,500 deg2sky area with a field of view (FOV) of 1.1 deg2in about 10 yr.It has a wavelength coverage from near-ultraviolet to near-infrared with seven photometric and three spectroscopic bands.Compared to other next generation surveys,the CSST has some advantages,e.g.,large FOV,wide wavelength coverage,high image quality and so on.It is expected to observe more than one hundred million galaxies from z=0 to 2 in its spectroscopic survey,which can precisely measure the evolution of the LSS and provide strong constraints on the MD theories.In this study,we will generate mock data of the CSST spectroscopic galaxy survey,and explore its capability in constraining the BD theory.

2.Basics of the BD Theory

In the BD theory,the coupling of gravity and matter is still preserved,thus the weak equivalence principle (WEP) is still unviolated,and all non-gravitational constants are unchanged.The action of BD theory in the usual frame is given by

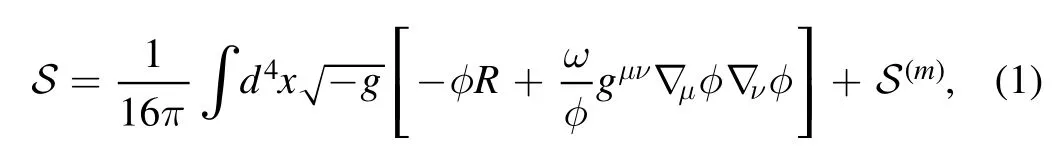
where the second term on the right-hand side is the action of ordinary matter fields,which is given bythe scalar field ϕ is the BD field and ω here is a dimensionless parameter.The results of Cavendish type experiments require that

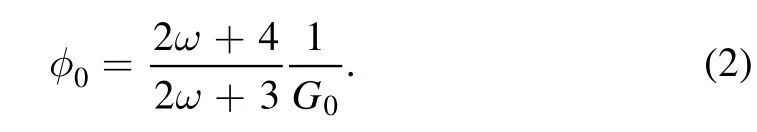
Here ϕ0and G0are the present values of BD field and the Newtonian gravitational constant respectively.For convenience,we can then define a dimensionless field

where G is the Newtonian gravitational constant,which is variable in the BD theory,and φ0=G0ϕ0.Thus,G is related to a scalar field,and the value of the field is determined by all matter in the universe.In other words,the Mach principle is satisfied.

In the limits of

BD theory can be reduced to GR.To ensure the continuity of its resulting range,we introduce a new BD parameter(Wu et al.2010)

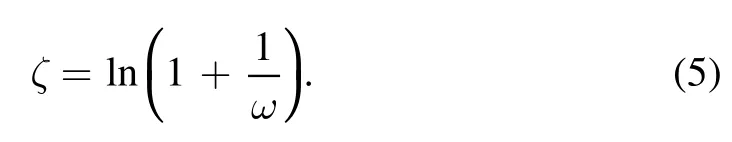
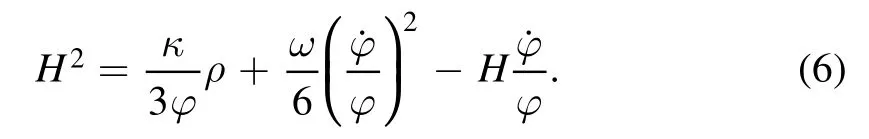
On the other hand,the calculation of the LSS evolution is much more complicated as shown in Wu et al.(2010),and we will discuss more details in the next section.In our BD cosmological model,for simplicity,we assume a flat universe with the CC as DE,which is supported by most of the current cosmological observations.

3.Mock Data and Model Constraints

If the BD theory is considered as the alternative of GR,the LSS evolution history and the interaction between galaxies will be different,and galaxy clustering is expected to be present in different patterns.In this section,we will discuss the utility of the galaxy clustering power spectrum measured by the CSST spectroscopic survey as an approach to constrain the BD cosmological model.

3.1.Mock Data of the CSST Galaxy Clustering Survey

The CSST will perform a spectroscopic survey using slitless gratings with spectral resolution R200,which contains three bands,i.e.,GU,GV and GI from 255 to 1000 nm.For any point sources,their AB magnitude 5σ limit is around 21 per resolution element or～23 for a band.We adopt the mock catalog result of the CSST spectroscopic survey from Gong et al.(2019),which is derived from the zCOSMOS catalog(Lilly et al.2007,2009).zCOSMOS is a redshift survey which performs the observations in the COSMOS(Capak et al.2007;Ilbert et al.2009) field using the VIMOS spectrograph on the Very Large Telescope.zCOSMOS has a similar survey depth as the CSST spectroscopic survey,and its magnitude limit is IAB⋍22.5 and it covers the whole 1.7 deg2COSMOS field.Totally about 16,600 high-quality sources with reliable spectroscopic redshifts are selected,which correspond to a galaxy surface density～2.7 arcmin-2.The mock galaxy redshift distribution in the CSST spectroscopic survey is displayed in Figure 1.We can find that the distribution has a peak at z=0.3–0.4,and it can extend to z～2.As we discuss later,due to statistical requirements,we only use the sources at z ≤1.5 when analyzing galaxy clustering.

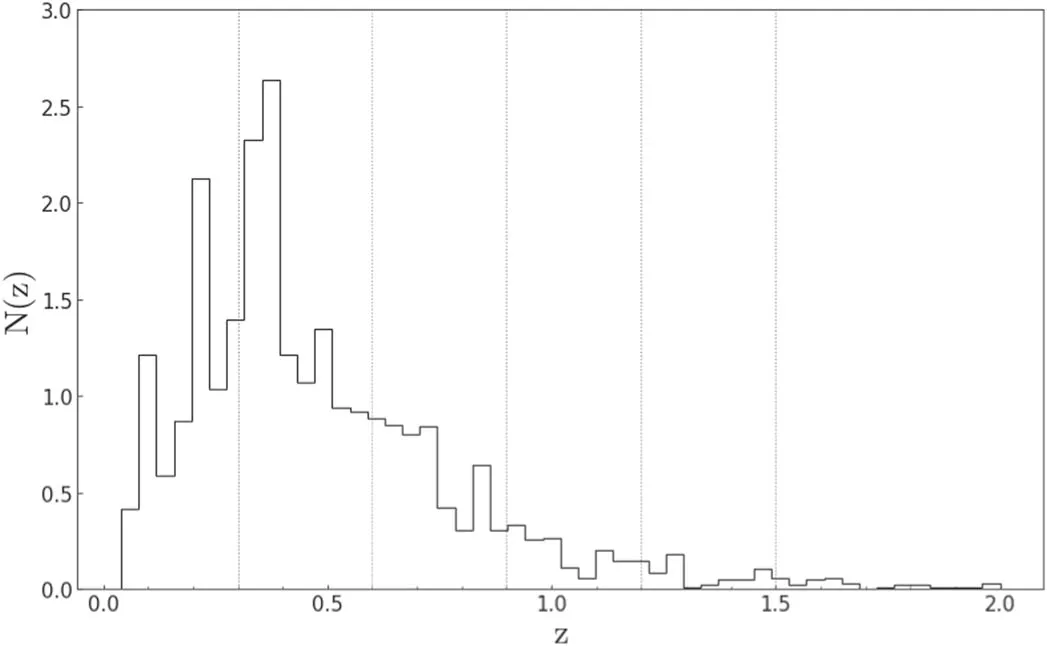
Figure 1.The mock galaxy redshift distribution of the CSST spectroscopic survey.The zCOSMOS catalog is adopted to derive the mock CSST spectroscopic galaxy catalog.The peak of the distribution is approximately at z=0.3–0.4,and the distribution can extend to about z=2.The vertical lines signify the boundaries of redshift bins.

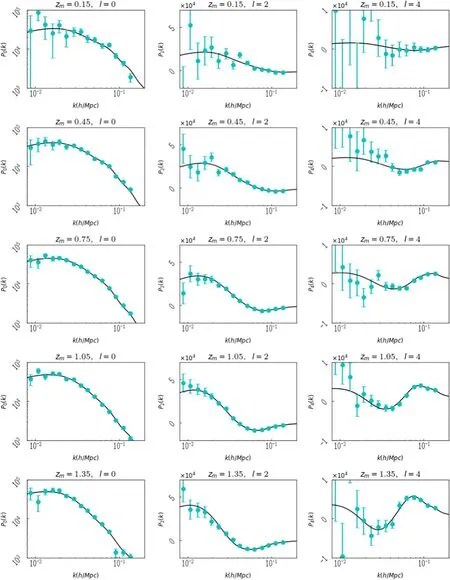
Figure 2.Galaxy mock multipole angular power spectra in the five spec-z bins.The three columns from left to right are P0g,P2g and P4g,respectively.The five rows show the five spec-z bins (zm denotes the central value of every bin).To mimic the statistical effect in the real measurements,the data points have been randomly shifted based on Gaussian distributions with the 1σ values as the data errors.

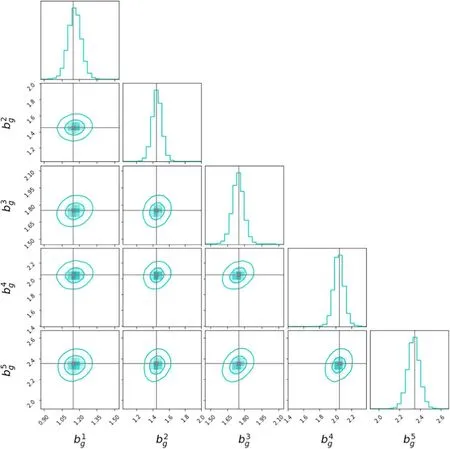
Figure 4.The 2D contour maps(68%and 95%CL)and 1D histograms of the posterior probability distributions of the galaxy bias in the five spec-z bins.The fiducial values of the parameters are also shown in gray lines.

The CSST spectroscopic survey measures the galaxy clustering in redshift space,and we will discuss the measurements of galaxy correlation function or power spectrum considering the effects of RSD.The redshift-space galaxy power spectrum can be expanded in Legendre polynomials(Taylor &Hamilton 1996)

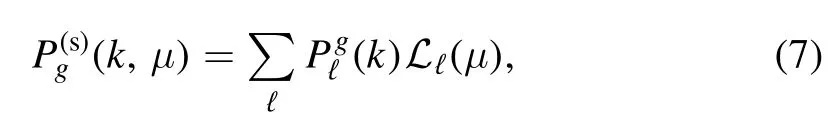
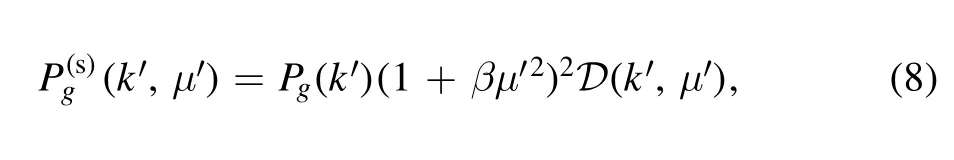
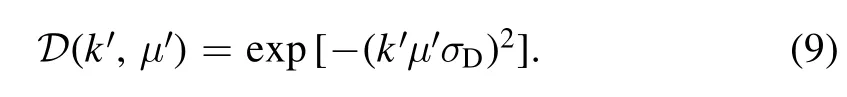
In consideration of the Alcock–Paczynski (AP) effect(Alcock&Paczynski 1979),one can write the galaxy multipole angular power spectra as

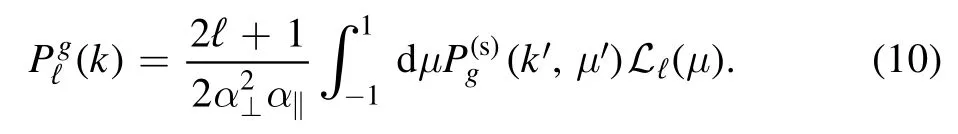
The scaling factors in the radial and transverse directions are given by

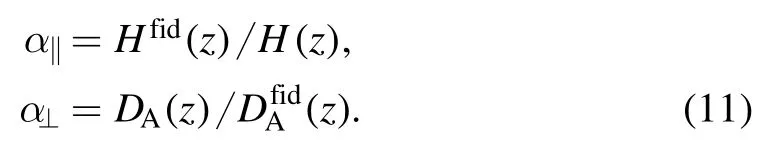
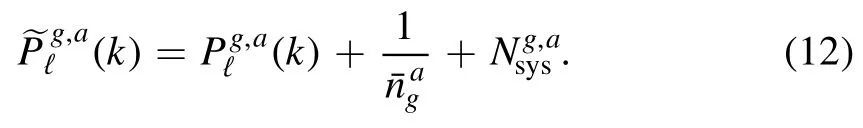
The superscript a denotes different spectroscopic redshift bins.To analyze the redshift evolution effect and obtain more information,we divide the redshift range covered by the CSST spectroscopic survey into five bins from z=0 to 1.5 as displayed in Figure 1.is the galaxy number density in a redshift bin.Considering that not all galaxies’redshifts in the CSST slitless spectroscopic survey can be measured well,an effective redshift-dependent fraction factoris included here.For simplicity,we assume

and we conservatively assumethat only half of galaxies at z=0 can have well-measured redshift with spec-z accuracy～0.002.From the mock CSST spectroscopic catalog which is mentioned earlier,we obtain that(Mpc/h)-3for the five spec-z bins.The systematic term is included for the instrumental effects of the CSST slitless gratings,and we set it as a constantwhich can be seen as an average value for all of the spectroscopic redshift bins and scales.After that,we can estimate the error by

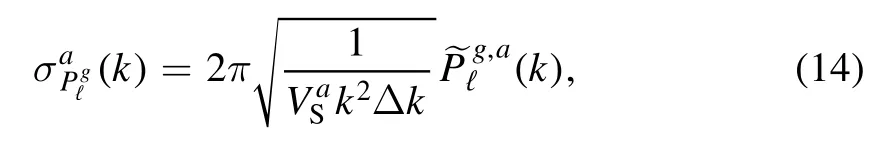
3.2.Fitting Method

After obtaining the mock data of galaxy clustering measurements in the CSST spectroscopic survey,we will constrain the parameters in the model by using these data.We consider 11 free parameters in the model,including one BD parameter ζ,five cosmological parameters,i.e.,Ωch2,Ωbh2,H0,Asand ns,and five galaxy bias parameters in the five spec-z bins.Ωbh2and Ωch2are the fraction of the total energy density of the universe contributed by baryonic matter and cold dark matter,respectively.H0is the Hubble constant,Asis the amplitude of primordial superhorizon power spectrum and nsis the scalar spectral index.After the fitting process,the derived parameters ΩΛandcan be obtained.Here ΩΛis the DE density,andis the ratio of the time derivative of Newtonian gravitational constant and the constant itself.The velocity dispersion parameters are not considered as free parameters here,since the velocity dispersion mainly impacts the non-linear regime that cannot significantly affect our results.Note that the resulting mock data of galaxy mock power spectra in the CSST spectroscopic survey are derived under the assumption of ζ=0,namely the case of GR.

The χ2statistical method is applied to fit our mock data,and the χ2is defined as

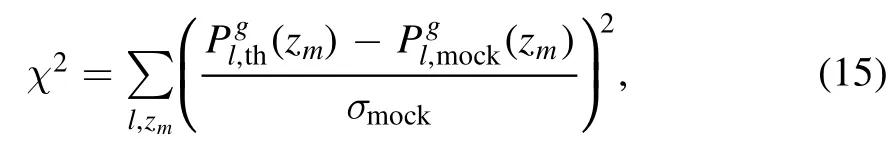
whereis the theoretical galaxy multipole angular power spectrum predicted from BD theory,is also the galaxy clustering power spectrum but from the mock data and σmockis the error.The summation is for all spec-z bins and different ls.Then the likelihood function can be estimated by,

The prospective constraint on the BD model can be derived by applying the Markov Chain Monte Carlo (MCMC)method.In our analysis,the MCMC is implemented by the publicly available code emcee (Foreman-Mackey et al.2013),which is based on the Goodman &Weares affine-invariant ensemble sampler for MCMC.The fiducial values of input parameters and the range of flat priors are shown in Table 1.

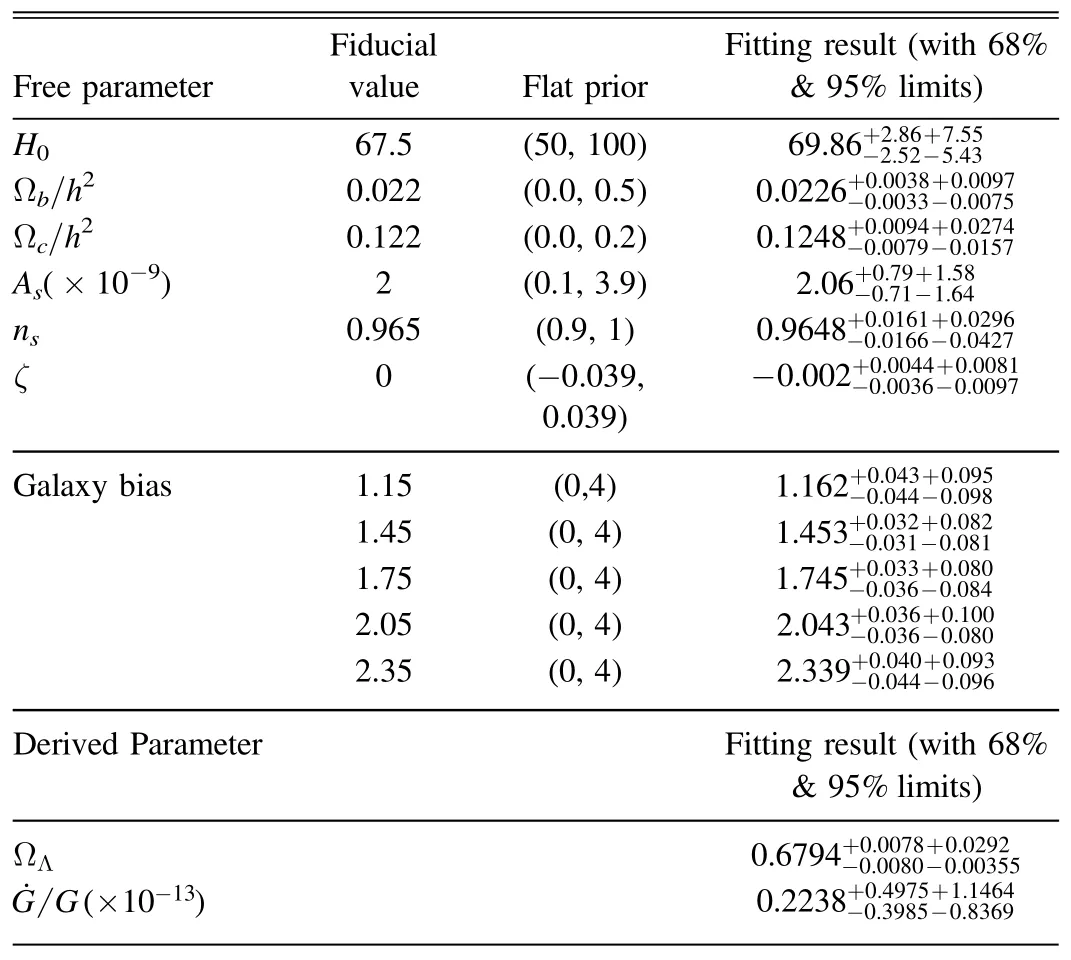
Table 1 The Fiducial values,Flat Priors,and Fitting Results of the Free and Derived Parameters in our Model

4.Results

After the MCMC fitting process,we have the constraint results of the free parameters in our BD model.The best-fits and 1σ and 2σ errors of the free and derived parameters are listed in Table 1.The 2D projected contour maps and 1D histograms of the posterior probability distributions of our BD cosmological parameters and galaxy bias are depicted in Figures 3 and 4,respectively.

We can find that the BD parameter ζ has been constrained as

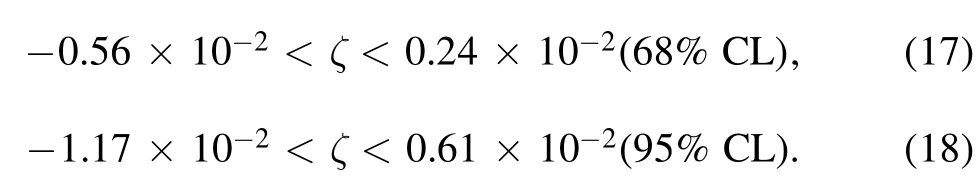
or the results can be converted to ω as

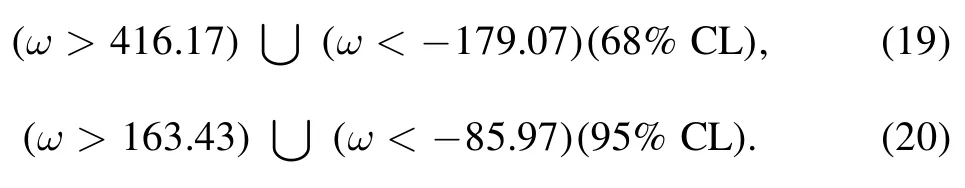
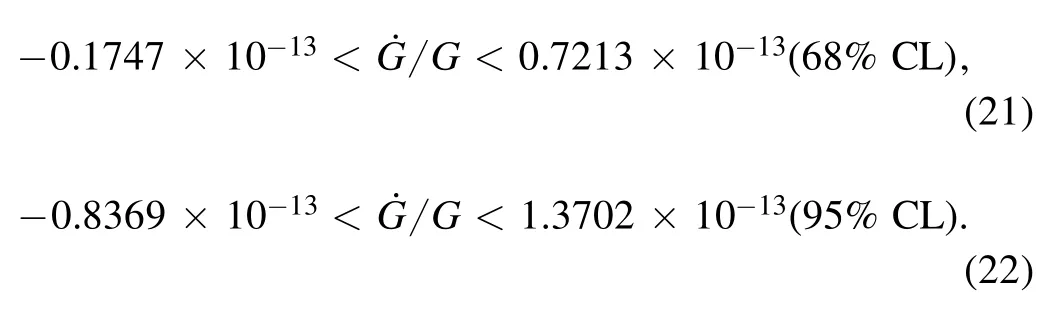
Compared to previous results,e.g.,the joint constraints by using CMB+BAO+SN Ia data(Li et al.2015),our constraints on ζ,ω orare at the same order of magnitude and comparable to the previous ones.Note that here we only consider the galaxy clustering measurement in the CSST spectroscopic survey,and the results can be further improved by including other CSST observations,such as weak and strong gravitational lensing,2D angular galaxy clustering,galaxy clusters,and so on.

Moreover,the constraints on the other cosmological parameters are also strong,especially for Ωch2,Ωbh2and H0,which are basically consistent with previous results in a Λ CDM universe with GR assumed (Gong et al.2019).In addition to the cosmological parameters,we also simultaneously constrain the galaxy bias parameters in different spec-z bins as displayed in Figure 4.We can find that the CSST spectroscopic galaxy clustering measurement can provide effective constraints on galaxy bias with an uncertainty around±0.1 (68% CL),which is also in good agreement with the results reported in Gong et al.(2019).The best-fits of galaxy biases also can be correctly derived.

5.Summary and Conclusion

In this paper,we test the ability of the CSST galaxy clustering spectroscopic survey in constraining the cosmology in the BD framework.We generate a mock catalog based on the zCOSMOS survey considering CSST instrumental and observational effects.The galaxy clustering multipole power spectra in different spec-z bins are calculated based on a modified CAMB code considering BD theory and RSD effect.The parameter ζ or ω of BD theory and other cosmological parameters are considered in the model.The galaxy bias parameters in different spec-z bins are also included and simultaneously constrained in the fitting process.The MCMC has been performed for fitting all eleven free parameters,and the contour maps and 1D probability distribution functions of the parameters are obtained.Finally,we get the constraint intervals of ζ,ω andWe find that the CSST spectroscopic galaxy survey can put strong constraints on the BD theory withwhich are at the same orders of magnitude compared to the constraints using current joint data sets of cosmological observations.The results can be further improved by including other CSST measurements,which indicate that the CSST can provide powerful surveys to constrain the BD theory and other MD theories.

Acknowledgments

A.D.C.and Y.G.acknowledge the support of MOST-2018YFE0120800,2020SKA0110402,NSFC-11822305,NSFC-11773031,NSFC-11633004,and CAS Interdisciplinary Innovation Team.F.Q.W.acknowledges the Chinese Academy of Sciences(CAS) instrument grant ZDKYYQ20200008,and the CAS Strategic Priority Research Program XDA15020200.Y.G.W.acknowledges National Natural Science Foundation of China(NSFC,Grant Nos.11773034 and 11633004),the Chinese Academy of Sciences (CAS) Strategic Priority Research Program XDA15020200 and the CAS Interdisciplinary Innovation Team(JCTD-2019-05).X.L.C.acknowledges the support of NSFC(Grant Nos.11473044 and 11973047),and the Chinese Academy of Science grants QYZDJ-SSW-SLH017 and XDB 23040100.