Constraining the Parameterized Neutron Star Equation of State with Astronomical Observations

Jaikhomba Singha,S.Mullai Vaneshwar,and Ankit Kumar

1 Department of Physics,Indian Institute of Technology Roorkee,Roorkee 247667,India;mjaikhomba@gmail.com

2 Department of Physics,National Institute of Technology Calicut,Kozhikode 673601,India

Abstract We utilize the phenomenologically parameterized piecewise polytropic equations of state to study various neutron star properties.We investigate the compliance of these equations of state with several astronomical observations.We also demonstrate that the theoretical estimates of the fractional moment of inertia cannot explain all the pulsar glitches observed.We model the crust as a solid spheroidal shell to calculate the fractional moment of inertia of fast-spinning neutron stars.We also show that the braking index obtained in a simple magnetic dipole radiation model with a varying moment of inertia deviates significantly from the observed data.Future developments in both theory and observations may allow us to use the fractional moment of inertia and braking index as observational constraints for neutron star equation of state.

Key words:stars:neutron– (stars:) pulsars:general– stars:rotation

1.Introduction

Neutron stars(NSs)are extremely dense objects formed as a result of violent supernova explosions of massive stars at the end of their lifetimes.Their extreme properties,such as strong magnetic fields,stable rotations,intense gravity,etc.,make them ideal laboratories to test various theories of physics under extreme conditions (Baym &Pethick 1979;Stairs 2003;Lattimer &Prakash 2004;Pizzochero 2016;Bandyopadhyay 2017).The observational manifestation of an NS is a pulsar.The internal structure and composition of NSs are governed by the equation of state (EOS) of neutron-rich matter (Lattimer &Prakash 2001).Despite extensive research,the composition of NS matter is not precisely known.While the primary constituents are neutrons and protons,the possible existence of hyperons and kaon condensates is still being debated.It is understood that the observation of most massive NSs could reveal some information about the presence of such exotic matter.A detailed study of EOS over a wide range of densities is crucial in understanding the properties of NSs.NSs are also continuously losing their rotational energy due to the emission of several highly energetic particles.This loss is reflected in the spin evolution of pulsars.The study of the spin evolution of pulsars helps in understanding the interior and the exterior of NSs (Urpin &Konenkov 1997;Staff et al.2012;Barsukov et al.2013).

In this work,we utilize the piecewise polytropic EOSs to study the various important properties of NSs.Several pieces of the relativistic polytropes are ensured to be thermodynamically continuous while mimicking various phase transitions at high densities.We further put various constraints on these EOSs obtained from observations.We show that the fractional moment of inertia (FMI) obtained from theory cannot explain all the observed glitches.We also investigate how FMI varies with rotational frequency.Finally,we demonstrate the deviation of the observed braking indices from their theoretical estimates.

The paper has been organized in the following manner.In Section 2,we briefly describe the structure of non-rotating and rotating NSs and the ways to estimate several NS properties like mass,radius,tidal deformability,FMI and braking index.In Section 3,we present the results obtained for the various EOSs used in the paper and discuss their implications.The several observational measurements used as constraints in this work have been listed in this section.Finally,in Section 4,we end the paper by presenting the conclusions of this work.

2.Formalism

The equilibrium configurations of NSs are usually calculated in two steps.The EOS of high-density matter is estimated at first,which is thereafter utilized for NS structure calculations in accordance with the principles of general relativity.In this work,we have constructed a few well-known EOSs based on the piecewise polytropic formalism (in Read et al.2009;Lackey 2021) for mimicking various phase transitions at high densities.

2.1.Structure of Non-rotating NSs

The structures of static and spherical NSs are governed by the following Tolman–Oppenheimer–Volkov(TOV)equations(Oppenheimer &Volkoff 1939;Tolman 1939):

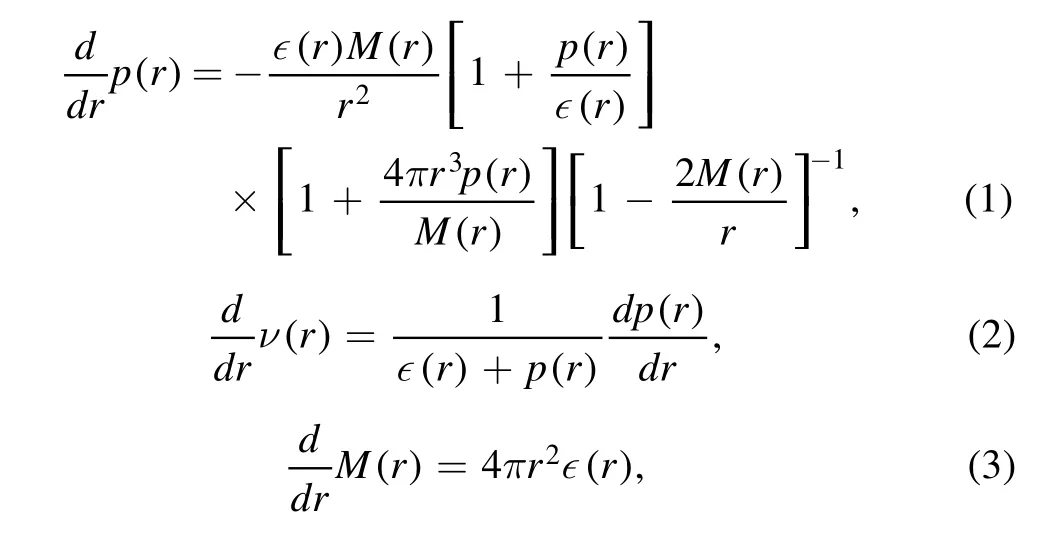
where M(r) is the enclosed mass of the NS within a radius r,and ν(r) is the metric potential.

2.2.Fractional Moment of Inertia of Slowly Rotating NSs

Assuming the NS to be rotating slowly,the moment of inertia (MOI) can be calculated within Hartle-Thorne’s approximation (Hartle 1967;Hartle &Thorne 1968).Under this condition,the metric takes the following form

where ω(r)is the frame dragging frequency.The NSs assume a nearly-spherical shape,and the MOI can be obtained as

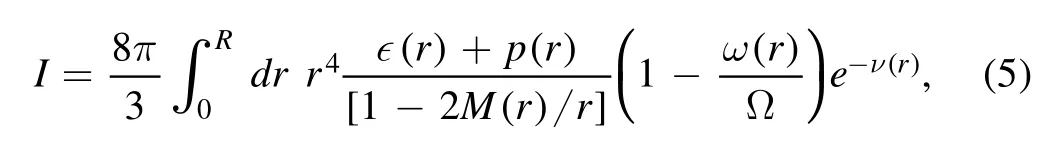
where Ω is the spin frequency of the NS.The crustal MOI has the same form

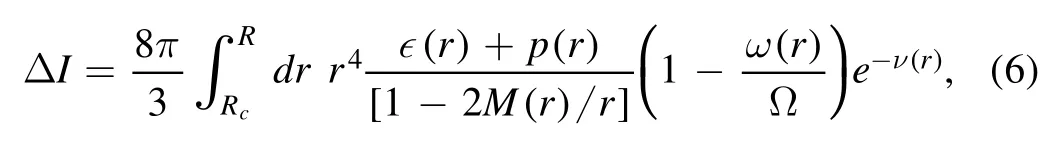
where Rcis the core-crust transition radius.The FMI is now defined as the ratio ΔI/I.

2.3.Tidal Deformability

An NS experiences a tidal gravitational field in the presence of a companion.The tidal deformability parameter is defined as(Hinderer et al.2010)

where Qijis the induced quadrupole moment,due to the tidal fieldεij.The tidal deformability can be expressed in terms of the Love number k2and the NS radius R as

The Love number k2is given by

where C=M/R is the compactness parameter,and yRsatisfies

The dimensionless tidal deformability can be defined as

2.4.Pulsar Braking Index

NSs emit electromagnetic energy via magnetic dipole radiation (MDR).This comes at the expense of the rotational kinetic energy,and hence the NSs are spinning down constantly with time.The pulsar braking index is related to the spin frequency as

In terms of spin period (P) and its derivatives,

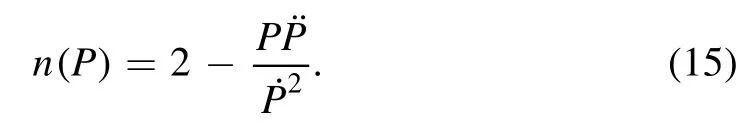
If we consider the MOI to be frequency independent,n=3(Kaspi et al.1994).However,the MOI varies with spin frequency,and hence it also varies with time (Glendenning et al.1997).Assuming the MOI to be frequency dependent we have (Hamil et al.2015)

2.5.Fractional Moment of Inertia of Fast Spinning NSs

For the special case of fast spinning NSs we calculate the equilibrium NS configurations in an axially symmetricspacetime.In this case the infinitesimal line element is given by

where N,A,B and Nϕare the metric functions dependent on r and θ.The numerical computations for solving the Einstein field equations are performed with suitable adaptation of LORENE libraries3https://lorene.obspm.fr/(Gourgoulhon 2011).The NS assumes a spheroidal shape,and the MOI for a rotation frequency Ω is given by

R(θ) is the NS radius in the θ direction and U is defined as

The baryon density profile is θ dependent,and so must be the core-crust transition radius Rc.We can therefore write the crustal MOI as

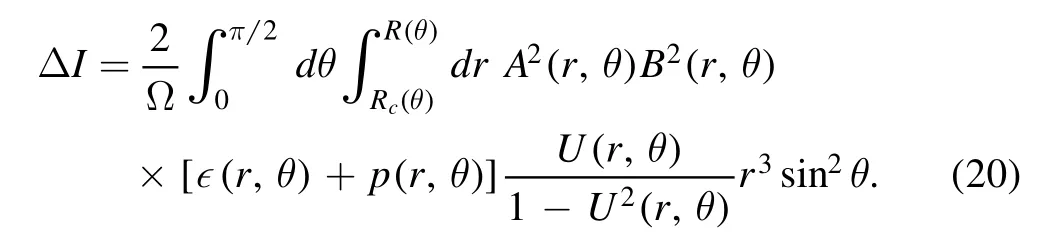
ΔI/I is defined as the FMI.

3.Results and Discussions

The NS interior is broadly divided into two major regions,i.e.,the crust and the core.The crust is primarily composed of nucleons,and is well understood because of its near-nuclear density.The core is highly compressed to many times the nuclear density,and despite extensive research,its composition and interactions are not precisely known.It is expected that the high-density matter in the NS core may show multiple phase transitions due to the sequential onset of exotic particles.

Following the seminal approach of Read et al.(2009);Lackey (2021),we have utilized the low density SLy EOS for the crust (Douchin &Haensel 2001),and the core is modeled with a variety of piecewise polytropes to emulate the expected phase transitions at high densities.This includes the ALF4(Alford et al.2005),AP3 (Akmal et al.1998),BBB2 (Baldo et al.1997),GNH3(Glendenning 1985),WFF3(Wiringa et al.1988) and SLy (Douchin &Haensel 2001) EOSs.ALF4 is a hybrid EOS with mixed Akmal-Pandharipande-Ravenhall(APR) nuclear matter and color-flavor locked quark matter EOS,AP3,and WFF3 are based on the variational method,BBB2 is a non-relativistic EOS and SLy is a potential-method EOS,with all of them modeling the npeμ matter.On the other hand,GNH3 is based on relativistic mean field theory,and takes into account the contribution of hyperons as well.The polytropic parameters of all the EOSs used in this work are taken from Read et al.(2009) and Lackey (2021).

There have been several efforts to constrain the NS EOS with astronomical observations and simulations.While the most common constraint is the measurement of the mass (see C0–C3 in Table 1),there has been good progress on the much awaited simultaneous estimation of the radius (see C4-C7 in Table 1).These serve as stringent limits on the allowed mass–radius configurations of stationary NSs.Figure 1 shows the mass–radius curves for various EOSs with the shaded regions depicting the various mass–radius constraints.WFF3 does not satisfy any,ALF4,BB2,SLy and GNH3 satisfy only some,and AP3 satisfies most of the mass–radius constraints.The inclusion of hyperons in GNH3 makes it a soft EOS,and this shows up in the comparatively large radii of the allowed configurations.The mass and radius obtained for the various EOSs match the results given in Read et al.(2009)and Lackey(2021).Any valid EOS must explain the existence of the most massive NS PSR J0348+0432,and hence C0 is a necessary constraint to comply with.It can be seen that the maximum allowed mass with ALF4,BBB2 and WFF3 is not high enough to satisfy the C0 constraint,hence we no longer include these EOSs in further discussions.

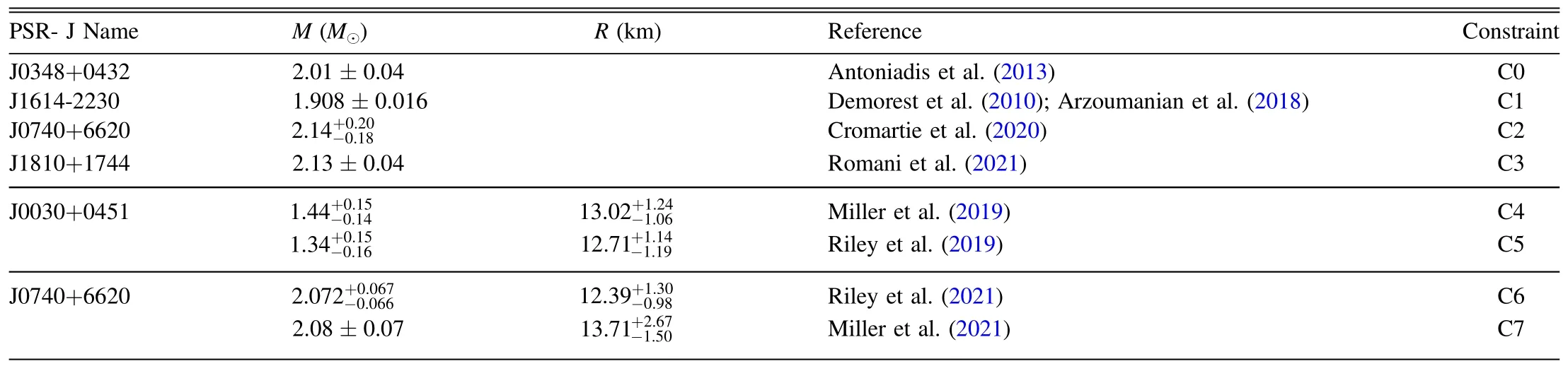
Table 1 NS Mass and Radius Constraints from Various Astronomical Observations

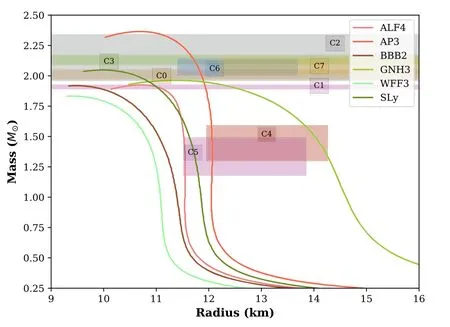
Figure 1.The mass–radius relations for the ALF4,AP3,BBB2,GNH3,WFF3 and SLy EOSs.The shaded regions depict the imposed mass–radius constraints from astronomical observations (see Table 1).

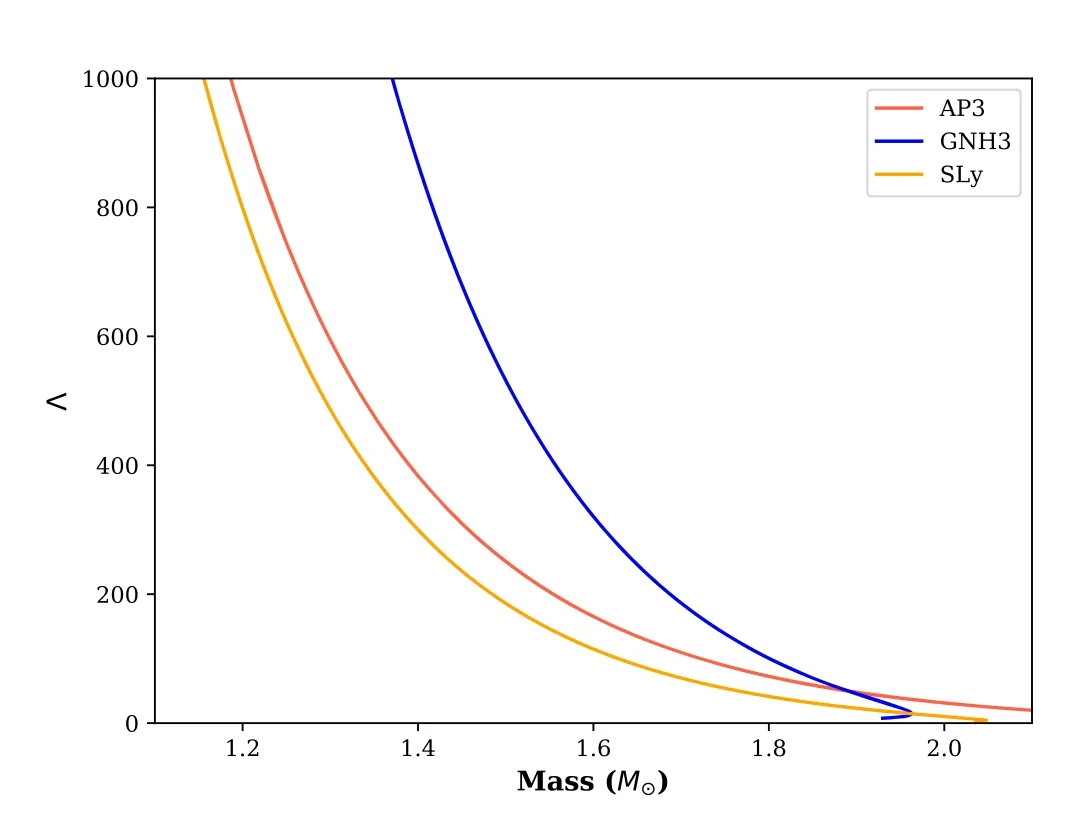
Figure 2.The dimensionless tidal deformability,Λ,as a function of NS mass for several EOSs.

LIGO-Virgo’s paradigmatic observation of the merger of two NSs (GW170817) quantified the response of NS matter toward a strong tidal gravitational field.It has been shown by Kumar et al.(2017),De et al.(2018),Ferreira &Providência(2021),Tan et al.(2021),Burgio et al.(2021)and many others that the determination of tidal deformability has been crucial in constraining the high-density EOS.The tidal deformability constraints utilized in this work are tabulated in Table 2.InFigure 2,we plot Λ as a function of the NS mass.GNH3 satisfies none,and AP3 and Sly satisfy all of the three deformability constraints.As expected from previous discussions,the NSs described by the soft GNH3 EOS will have smaller compactness,and hence a larger Λ.The compliance of all the EOSs with the imposed constraints is summarized in Table 3.It can be seen that AP3 satisfies the maximum number of constraints.It explains the existence of the massive pulsar PSR J0348+0432(Antoniadis et al.2013).

Figure 3.The FMI as a function of NS masses (left) and radii (right) for several piecewise polytropic EOSs resembling the realistic EOSs:AP3,GNH3 and SLy.

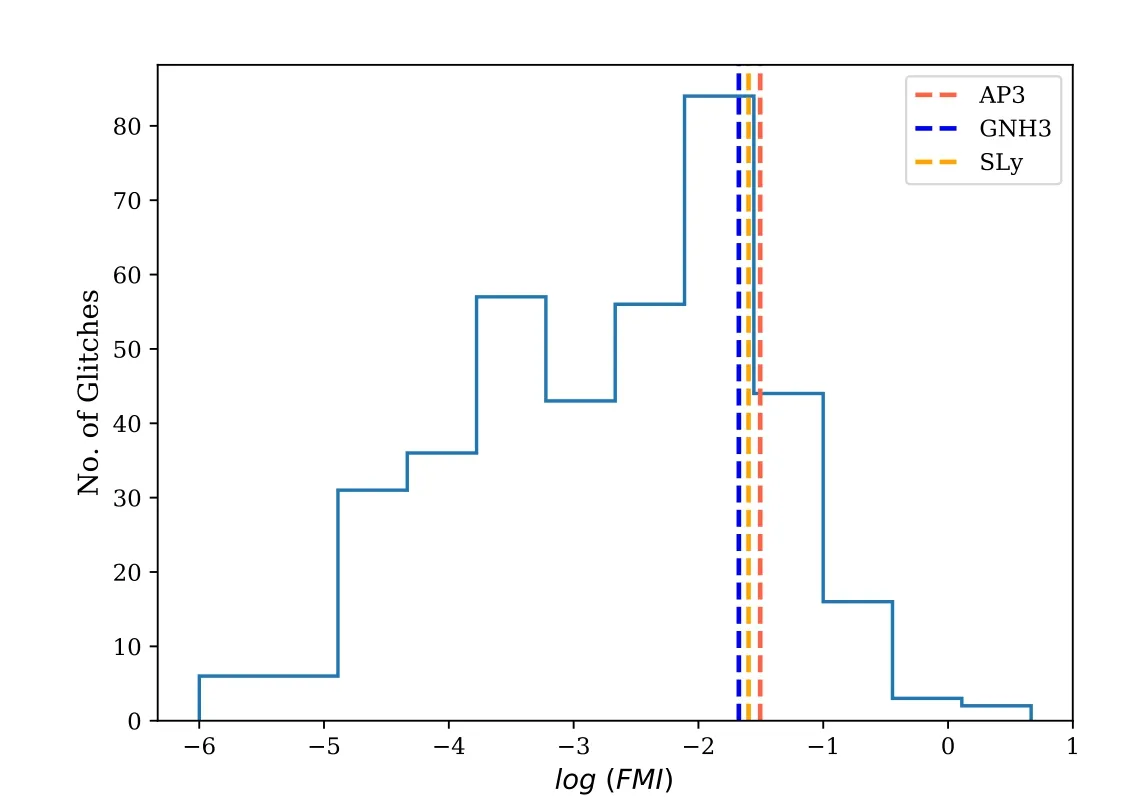
Figure 4.Distribution of the FMI obtained from different glitch observations cataloged by the Jodrell Bank Observatory.The dashed lines signify the FMI obtained for the various EOSs for a canonical NS.

Table 2 Gravitational Wave Constraints on the Dimensionless Tidal Deformability Λ

Table 3 Compliance of various EOSs with the Imposed Mass (C1–C3),Mass–Radius(C4–C7) and Tidal Deformability Constraints (C8–C10)

We now discuss some other properties of NSs viz.,FMI and braking index.There are times when an NS suddenly spins up.Such an event is called a pulsar glitch (Radhakrishnan &Manchester 1969),and their observations help in various ways to probe the interiors of NSs (Link et al.1992;Gügercinoğlu 2017;Haskell 2017).Presently,the most favorable model to explain the occurrence of a pulsar glitch is based on pinning of superfluid vortices in the NS crust(Haskell&Melatos 2015).It is believed that glitches occur due to the transfer of angular momentum from the interior to the outer crust.The ratio of the MOI of the crust and the core,i.e.,FMI,can be estimated from observations of pulsar glitches (Basu et al.2018)

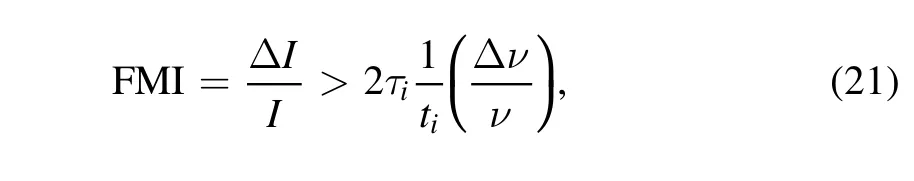
where τiis the characteristic age of the pulsar,tiis the time preceding the last glitch and Δν/ν is the fractional rise in the spin frequency.As mentioned in Sections 2.2 and 2.5,FMI can also be estimated for a given EOS for both slowly rotating and fast rotating NSs.

Figure 3 displays the FMI as a function of the NS mass and radius in the slow rotation limit.The crust-core transition density for every EOS ranges from 6.659×1013to 2.014×1014g cc−1.It is seen that FMI is the lowest for GNH3.Since FMI can bededuced from observations,it can be utilized to constrain the NS as well.However,the FMI estimated for a particular EOS cannot explain all the glitches observed.Many studies suggest that in order to explain some of the glitches,the participation of superfluidity in the core along with crustal superfluid must be invoked (Andersson et al.2012;Basu et al.2018).Although there has been some progress in theorizing superfluidity inside NS cores(Andersson&Comer 2001;Takatsuka et al.2006),we do not explore this in the present work.Figure 4 shows the distribution of FMIs of 384 glitches from the Jodrell Bank pulsar glitch catalog.4https://www.jb.man.ac.uk/～pulsar/glitches/gTable.htmlSince FMI cannot be estimated for the first glitch,we exclude the first glitch of every multiple glitching pulsar and also the pulsars with only one glitch.Assuming a canonical NS,for a fraction of glitches ¯f,the observed FMI is larger than what is estimated under the slow rotation approximation (see the dotted lines in Figure 4).The values off¯obtained for the various EOSs are summarized in Table 4.It can again be seen that AP3 explains the most number of glitches,while GNH3 explains the least.For these glitches,it is expected that there is a contribution of superfluidity in the NS cores.It is important to point out that we have excluded the effect of entrainment.Presently,the FMI does not put very strong constraints on the EOS.Future advancements in theoretical studies along with better observational facilities may allow us to use FMI as a constraint for the NS EOS.

Table 4 The Fraction of Glitches Which Cannot be Explained with the Estimated FMI from the EOSs for a Canonical NS

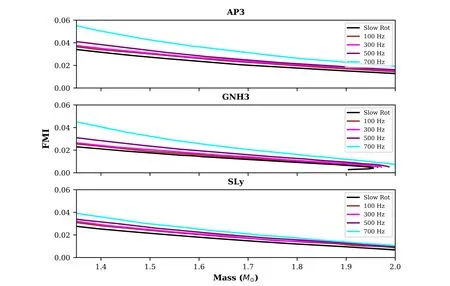
Figure 5.The FMI as a function of NS mass for different rotation frequencies.M⊙is the solar mass and the frequencies are mentioned in the legends.The calculations for the slowly rotating case are performed with in the Hartle–Thorne approximation(as discussed in Section 2.2).The results for the fast rotating cases are calculated exactly with a suitable adaptation of LORENE libraries (see Section 2.5).

Table 5 The Braking Index Values Obtained from Several Pulsar Observations

In a first,we explore the variation of FMI at very high rotation rates.Figure 5 plots the FMI as a function of NS masses at different frequencies.The FMI does not vary with the frequency in the slow rotation approximation.We demonstrate a monotonic increment in the FMI with an increase in the spin frequency.We have limited our calculations up to 700 Hz,which is close to the spin frequency of the fastest spinning radio pulsar observed at 716 Hz (Hessels et al.2006).At this frequency,Sly shows the least deviation.The centrifugal force on a spinning object is proportional to its distance from the rotation axis.The crust is the outermost region,and hence with an increase in spin frequency,ΔI changes relatively faster than I.This leads to an overall increment of the ratio ΔI/I.

Figure 6.The braking index as a function of NS rotation frequency for the various EOSs.

Another quantity that we have explored is the pulsar braking index.NSs are constantly radiating electromagnetic energy via MDR.This comes at the expense of the rotational kinetic energy,and hence the NSs are continuously slowing down.The braking index quantifies the rate of decrease of spin frequency.Considering the MOI to be frequency dependent,the braking index is given by Equation(16).The braking indexes of several pulsars have been estimated with the help of long baseline timing programs and other astronomical observations,and some of them are summarized in Table 5.It is evident that for many of these young pulsars,the braking index is much lower than 3.The braking index obtained for a 1.4 M⊙NS as a function of rotational frequency is displayed in Figure 6.The braking index varies very slowly and deviates a lot from the observations.Thus,an MDR model with a varying MOI may not be sufficient to explain the observed pulsar braking indices.It is shown by Lyne et al.(2013),Tauris &Konar (2001),Johnston &Karastergiou (2017) and many others that the braking index depends on various factors like the temporal evolution of the magnetic field strength and the inclination angle between the magnetic and rotational axes.Although the braking indices of young pulsars are expected to be less than three,several estimations demonstrate that it can be greater than three as well (Archibald et al.2016;Parthasarathy et al.2020).Even decades after the discovery of pulsars,the braking index is still not understood very well.The measurements of braking index presently do not provide strong constraints for the NS EOS.Future advancements in pulsar emission theory and its relation with the NS EOS will help in utilizing such observations in constraining the NS EOS.

4.Conclusions

In order to understand the interior structure of NSs,it is necessary that we constrain the EOS with the maximum possible number of constraints from nuclear experiments and astronomical observations.In this work,we utilized several piecewise polytropic EOSs to check their compliance with astronomical observations.We demonstrated that a significant fraction of glitches cannot be explained with the FMI obtained for any of the EOSs.We modeled the NS crust as a solid spheroidal shell to calculate the FMI at high frequencies.We showed that the FMI increases monotonically with an increase in the rotation rate.Furthermore,we investigated the variation of braking index in the MDR model,and showed that it cannot explain the observed data.The FMI and the braking index cannot be used to constrain the NS EOS but,with advancements in observational facilities,it may be possible in the near future.

Acknowledgments

This work is partly supported by the SPARK program of IIT Roorkee (India).J.S.acknowledges various discussions with V.B.Thapa.We thank P.Arumugam for his comments during the preparation of this manuscript.The authors especially thank the anonymous referee for their constructive comments which have improved the presentation of this article.

ORCID iDs