基于霍夫变换的旋转长基线干涉仪雷达信号分选算法

李江浩 ，季华益 ，罗佳奕，周 钧 ，余仲阳 ，李煊鹏

（1.中国航天科工集团8511 研究所，江苏 南京 210007；2.东南大学仪器科学与工程学院，江苏 南京 211189）

0 引言

信号分选是将时域上相互重叠的多部雷达脉冲序列重新划分为多个独立脉冲序列的过程，作为雷达信号侦察数据处理的基础和关键技术，历来受到国内外广泛关注。基于脉冲描述字（PDW）的信号分选方案通常分为预分选和主分选2 层。预分选阶段利用常规雷达脉冲载频（RF）、脉宽（PW）、到达角（AOA）等参数短时间内保持不变的特性，对相关参数进行聚类实现初步分选，采用的聚类方法包括基于密度的DBSCAN 聚类方法、基于统计的网格聚类方法和基于机器学习的支持向量机聚类方法。主分选阶段利用脉冲TOA 参数估计辐射源脉冲重复间隔（PRI）实现分选，主要方法包括动态关联法、脉冲时差直方图法、PRI 变换法和平面变换法。随着电子技术的发展，雷达辐射源数量急剧增多，脉间调制方式日益复杂，使基于固定参数的分选方法受到很大挑战。

旋转长基线干涉仪（RLBI）通过自身基线旋转测量各个方向上辐射源信号的相位差，累积一段时间内相位差数据以估计来波方向。与传统固定基线阵列干涉仪相比，旋转基线干涉仪只需要双阵元即可完成测向，系统复杂性和通道一致性要求低。为提高定位精度，旋转干涉仪基线长度通常远大于信号波长，导致脉冲相位差测量存在模糊，无法直接估计来波方向，在预分选阶段无法利用AOA 参数，准确性严重下降。文献[8]提出了一种基于多次模糊测相结果的多假设非线性最小二乘测向算法，能够利用3 次脉冲相位信息完成测向，但是多目标情况下必须首先进行信号分选。文献[9]针对阵列旋转干涉仪测向提出了一种基于多重信号分类算法估计目标角度和利用角度曲线霍夫变换进行解模糊的多目标测向方法，但仅能应用于目标数量小于阵列数量的情况，无法用于一般干涉仪测向。文献[10]提出了一种基于机械扫描天线工作时脉冲幅度呈抛物线变化规律的脉冲序列提取方法，但是无法应用于电扫描天线。

针对以上问题，本文提出了一种将多分辨率网格聚类和霍夫变换相结合的信号分选方法：首先对脉冲频率进行聚类，区分不同频率辐射源，降低信号交叠程度；再将脉冲映射到时间-相位图像中，可见同一脉冲序列的相位参数短时间内呈分段线性变化，利用霍夫变换提取图像中的线性特征，检测不同来波方向的信号；最后利用相位周期延拓，合并同一脉冲序列对应的多条时间-相位线段，完成信号分选。仿真实验证明了方法的有效性。与传统方法相比，本方法在能够在分选阶段区分不同方位的脉冲序列，在一定程度上减小了辐射源PRI 调制方式变化对分选造成的影响，具有更高的可靠性。

1 旋转干涉仪测向模型

旋转干涉仪测向模型如图1 所示。定义干涉仪参考阵元位置为原点，基线旋转平面为平面，建立空间直角坐标系。干涉仪基线长度为，绕原点逆时针旋转，角速度为。辐射源位于点，定义辐射源方向矢量在平面上的投影与轴正方向的夹角为方位角，与基线旋转平面的夹角为俯仰角。随着基线旋转，辐射源信号相位差因入射方向变化而周期性变化。

图1 旋转干涉仪测向模型

假设= 0 时刻基线的旋转角为，则基线方向向量的表达式为：

在远场条件下，辐射源电磁波可以认为是平面波，则来波方向上的单位矢量可以表示为：

雷达脉冲信号持续时间通常远小于基线旋转周期，在信号持续时间内，可以认为基线的位置是固定的。根据固定基线干涉仪远场测向模型，可以得到两阵元接收信号的相位差Δ为：

定义=cos/，=-，可以将相位差表达式改写为：

由式(4)可知，目标信号的相位差呈余弦规律变化，如图2 所示。其中幅度由基线长度、波长和俯仰角共同决定，初相由方位角决定。

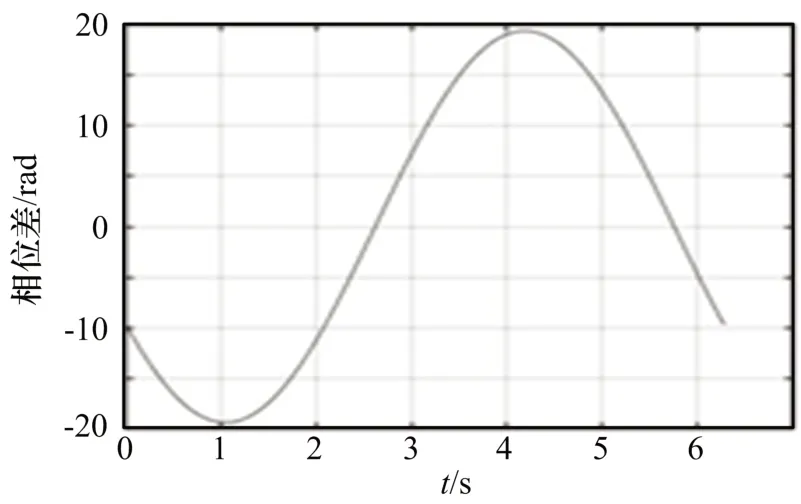
图2 辐射源信号相位差

当大于1 时，阵元间相位差超过2π，导致相位差测量出现模糊，此时相位差测量值表达式为为：

为提高旋转干涉仪测向精度，通常有≫，导致相位曲线的幅值远大于1，使部分区间内辐射源相位曲线由余弦曲线退化为直线。此时辐射源脉冲信号相位差测量结果如图3 所示。

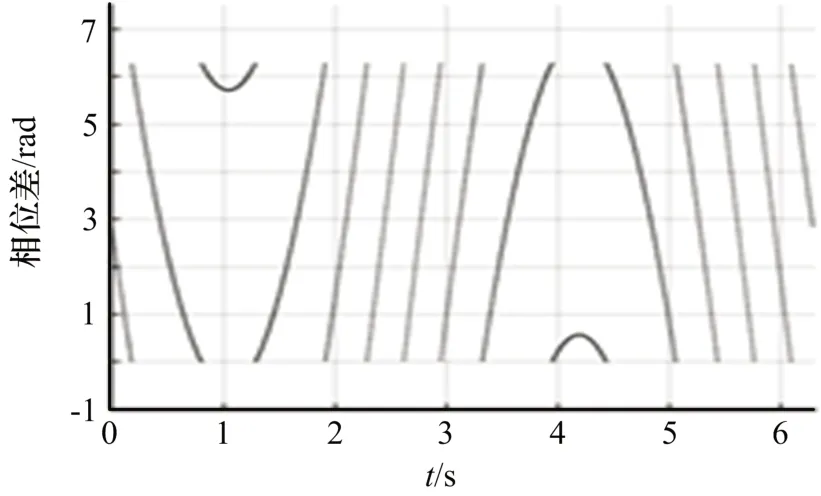
图3 辐射源信号相位差测量结果

在多目标情况下，不同位置、频率的辐射源脉冲序列相位变化特征不同，其特征如图4 所示。在图4（a）中，多目标脉冲序列的真实相位差呈现为多条正弦曲线，其幅度和初相参数分别对应了信号频率、俯仰角和方位角。在图4（b）中，由于相位模糊的影响，相位差在干涉仪测量结果在部分区间仍然保持明显的正弦曲线变化特征，在大多数区间内退化为多条相交的直线。通过检测属于同一脉冲序列的相位变化曲线，可以分选多目标情况下不同位置、频率辐射源信号。

图4 多目标信号相位差

2 基于频率和相位的信号分选算法原理

根据以上分析，本文采用频率预分选、时间-相位主分选和脉冲提取的3 层分选方案。下面对每一层的分选作详细说明，算法流程如图5 所示。

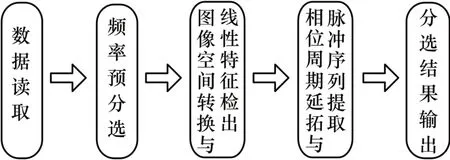
图5 基于频率和相位的辐射源信号分选流程

2.1 频率预分选

雷达脉冲信号在频率上的分布特性受到辐射源数量、辐射源工作频率、接收机测频精度等多种因素影响，不同时刻、频段下信号频率的分布特性存在差异，采用固定参数的聚类方法难以满足所有情形。因此本文采用基于自适应阈值的多分辨率网格空间聚类算法。

网格空间聚类算法首先将频率区间分割为多个互不重叠的子区间，计算各个区间内脉冲的数量，根据统计结果计算自适应阈值，将子区间分为有效区间和噪声区间。基于网格统计的结果，将相邻的有效区间聚为一类，对载频跨度较大的聚类做进一步分割和聚类，得到最终的聚类结果。聚类算法步骤如下：

输入：脉冲频率，首次统计时的区间长度，需要进一步聚类的区间长度，最多迭代分割次数。

输出：区间分割结果。

Step1：根据接收机工作频带将脉冲频率数据归一化，方法为=（-）/（-），其中、分别为脉冲频率最大值和最小值。

Step2：均匀划分待聚类频率区间，长度为, 首次划分时=。

Step3：统计每个频率区间内的脉冲密度。

Step4：计算自适应阈值，将网格标记为高峰区间和低谷区间。

Step5：合并连续高峰区间。

Step6：如果区间长度大于l，重复Step2—Step5，直到迭代分割次数达到。

本方法使用一维最大类间方差法计算出类间区分度最大的阈值。最大类间方差将统计区间划分为高峰频段和低谷频段，并统计高峰频段和低谷频段脉冲数量之间的方差。高峰频段和低谷频段的类间方差越大，说明高峰频段和低谷频段之间的脉冲数量差异越大。当类间方差达到最大时，频段划分效果最好，此时选取的阈值为最佳阈值。

类间方差的定义为：

式中，为类间方差，为所有区间脉冲数量均值，和分别为高峰区间和低谷区间的脉冲数量均值，和分别为高峰区间和低谷区间数量占总区间数量之比。

本文采用搜索法计算最大类间方差，步骤如下：

Step1：统计当前待划分频段内频率区间脉冲数最大值和最小值，将=[,]，作为候选阈值集合。

Step2：遍历所有候选阈值，将频率区间划分为高峰区间和低谷区间，计算每个阈值对应的类间方差。

Step3：获取Step2 中类间方差最大时对应的候选阈值，将其作为最佳阈值，得到区间划分结果。

2.2 图像空间转换与线性特征检出

图像空间转换是将脉冲流转换为到达时间-相位(TOA-PH)二维图像的过程，脉冲TOA-PH 图像如图6 所示。针对频率预分选过程输出的某个有效频段，首先将TOA-PH 空间离散化为均匀且不重叠的网格，统计每个TOA-PH 网格内脉冲的数量,获得二维统计直方图，进行归一化操作，得到如图6（a）所示TOA-PH 灰度图像。灰度较高说明该时间段内脉冲密度较大，存在辐射源信号的可能性大。经过图像转换，将时间域中信号相位随基线旋转的变化特征转换为图像空间中时间-相位直线几何特征。

为提高分选准确率，采用中值滤波对灰度图像进行降噪处理。在灰度图像中，各个脉冲信号的时间密度不同，使得灰度图像中部分信号的直线特征不明显，因此采用最大类间方差法对图像进行二值化处理。通过二值化处理，将网格分成有效（存在信号）和无效（不存在信号）2 部分，去除部分噪声点，提高直线特征检测准确率。滤波后TOA-PH 图像如图6（b）所示。

图6 脉冲TOA-PH 图像

现有的直线检测方法主要有基于梯度信息的直线检测算法和基于霍夫变换的直线检测算法。基于梯度信息的直线检测方法主要是对局部区域内梯度方向一致的像素点进行合并，达到检测直线的目的。此方法具有参数自适应性，并且检测精度高。但在TOA-PH 图像中，多个辐射源脉冲序列的相位特征直线存在交叉和重叠，使用梯度检测容易得到错误的检测结果，且由于图像背景单一，梯度信息较难有效利用。因此本文采用基于霍夫变换的直线检测算法。

霍夫变换检测是一种全局的拟合算法，主要通过拟合给定曲线的参数方程完成曲线检测。霍夫变换将给定曲线方差的未定参数组成的空间称为霍夫空间，运用2 个坐标空间之间的变换，将在一个空间中具有相同形状的曲线或直线映射到另一个坐标空间的一个点上形成峰值，从而把检测任意形状的问题转化为霍夫空间内统计峰值问题。

在二维TOA-PH 平面中，每个脉冲PDW对应一个点(x, y)，2 个脉冲 PDW和 PDW可以在 TOA-PH平面中确定一条直线，称为相位直线。得到相位直线如图7 所示，其方程的表达式为：

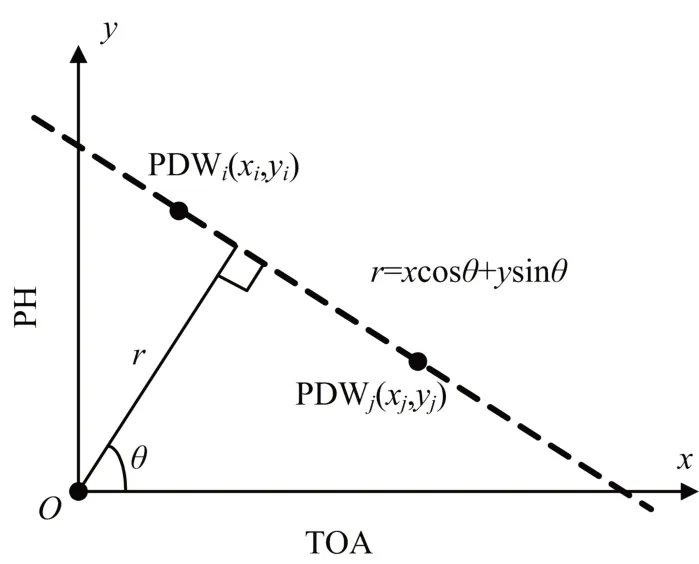
图7 TOA-PH 平面内相位直线

式中，为直线离原点的距离，为直线到原点的垂线的方向角。

根据以上推导，可以相同方式将TOA-PH 平面内的单个点在霍夫平面内映射为一条正弦曲线。多个位于同一条直线上的点满足相同的直线参数方程，在霍夫平面内体现为其对应的霍夫曲线相交于一点，直线霍夫变换示意图如图8 所示。同一交点经过的曲线越多，说明该交点对应相位直线上的点越多，存在直线特征的概率越大。选择可能存在直线的参数网格，将有效参数网格对应的直线参数重新映射到TOA-PH 平面内，得到原平面中可能存在的直线。计算该直线上数据点的距离，将相邻的数据点连接成线段，得到原平面中的线段检测结果。

图8 直线霍夫变换示意图

2.3 相位周期延拓与脉冲序列提取

图 9 为周期延拓前后 TOA-PH 图像。图 9（a）显示了某个频段内霍夫直线检测结果。由于相位模糊的影响，单个辐射源脉冲相位曲线被分割为多条模糊点迹，为提取该辐射源所有脉冲，需将属于同一脉冲序列的模糊点迹合并。考虑相邻模糊点迹在相位跳变点处对应的TOA 相同且斜率相似，对相位进行周期延拓，即将当前时段内所有脉冲相位由[0, 2π)延展到[0, 4π)，延拓后图像如图 9（b）所示。每个 TOA-PH数据点经延拓都会在[2π, 4π)区域相同位置处出现一个副本，同一辐射源对应的模糊点迹和另一条模糊点迹的副本近似呈一条直线，可由此判断其是否属于同一个辐射源。

图9 周期延拓前后TOA-PH 图像

从图9（b）可看出，由于脉冲TOA 和相位参数存在随机误差，脉冲序列相位点迹存在一定宽度和断裂，导致同一条点迹在检测结果中分成多条细碎线段。为提取同一辐射源的线段，需要对细碎线段进行聚类。同一簇的线段的方向相近，但起点和终点位置存在较大差异。为消除起点和终点位置差异的影响，将线段两端延长，截取PH=π 和PH=3π 之间的部分，截取后的霍夫线段如图10 所示。同一点迹上的霍夫线段截取后上下端点集中于同一位置；同时不同点迹上的霍夫线段上下端点仍然位于不同位置。进而使用二维DBSCAN 算法对端点位置进行聚类，合并同一点迹上的多条霍夫线段。图11 展示了从霍夫线段到辐射源的2 层聚类流程。

图10 截取后的霍夫线段

图11 霍夫线段聚类处理流程

在延拓后的TOA-PH 图像中，每一条霍夫线段都会在原图像区域和延拓区域内各出现一次。经过聚类后，位于原图像区域的霍夫线段与前一条相位直线上的霍夫线段聚为一类，同时位于延拓区域的霍夫线段与后一条相位直线上的霍夫线段聚为一类。因此，通过检测2 条霍夫直线是否包含同一条霍夫线段，可以合并为同一个辐射源。

本文采用最近邻法提取同一辐射源脉冲序列：首先计算脉冲和已提取的相位霍夫线段之间的距离，判断脉冲是否与TOA-PH 空间中的某条霍夫线段相关联，然后根据霍夫线段与辐射源间的对应关系得到辐射源脉冲序列。具体步骤如下：

输入：脉冲距离门限。

输出：辐射源脉冲序列。

Step1：在TOA-PH 空间中对PDW 数据点和检测得到的霍夫线段归一化。

Step2：根据霍夫线段的起点和终点，重新计算其表达式=cos+sin。

Step3：计算每个脉冲到各个霍夫线段的距离，并统计最小值。若小于，将脉冲标记为与其最近的霍夫线段序号，否则脉冲不属于任一霍夫线段，标记为0。

Step4：将所有脉冲标记后，根据霍夫线段聚类结果合并同一辐射源所属霍夫线段对应的脉冲，得到提取结果。

3 仿真分析

为验证算法有效性，建立旋转干涉仪模型并进行分选仿真实验。设置旋转干涉仪基线长度为2 m，旋转速度为0.5 rad/s，初始相位为0°。接收机工作频率为3 000 MHz，带宽为100 MHz。辐射源参数如表1所示，假设脉冲频率、相位等参数测量无系统误差，且随机误差服从高斯分布，脉冲相位测量均方误差为10°，载频测量均方误差为0.5 MHz。

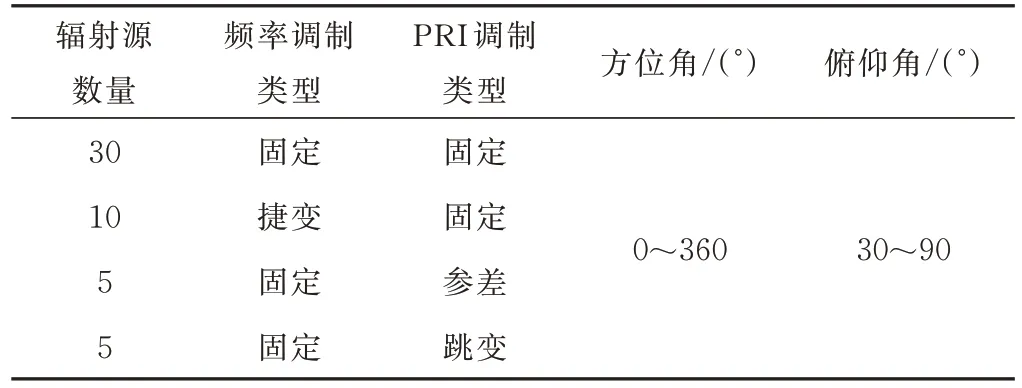
表1 仿真辐射源参数

3.1 频率预分选

设置首次划分区间长度= 1 MHz，最大迭代分割次数为2，需要再次分割的连续区间长度为5 MHz。首次分割后，频率直方图如图12 所示。

图12 脉冲频率分布直方图

经过网格聚类，接收机工作频段被分割为21 个有效区间，结果如图13、图14 所示。图中有效区间起始值用红色直线表示，终止值用黑色直线表示。

图13 初次聚类结果

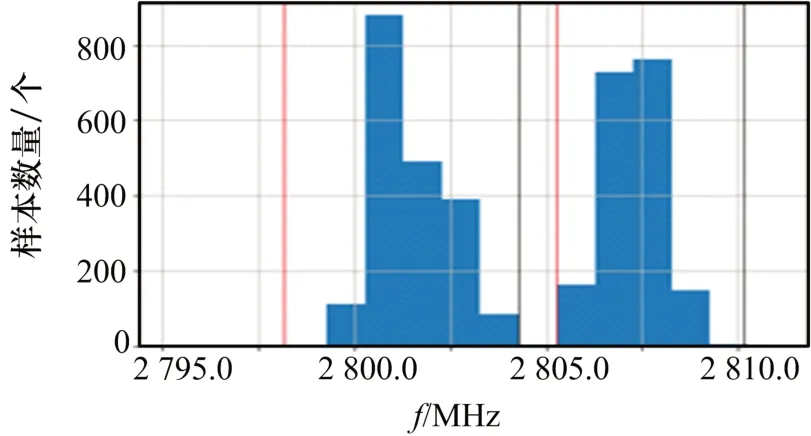
图14 某个连续区间二次聚类结果

根据聚类结果，频率预分选步骤能够区分不同频率的辐射源脉冲，从而降低了TOA-PH 空间的脉冲密度，提高了相位直线检测结果的准确性。

3.2 相位直线检测

选取有效频段，统计频段内的脉冲在TOA-PH 平面内的分布，得到如图15 所示的TOA-PH 灰度图像。使用中值滤波和OTSU 大津算法进行降噪和二值化处理，利用霍夫变换检测TOA-PH 空间中的相位直线。

图15 TOA-PH 灰度图像

图15—17 展示了某个有效频段内脉冲相位直线提取结果，该频段内存在3 个辐射源。比较图15 和图16，可见滤波后的二值化图像中相位直线特征更加明显。图17 用不同颜色的直线标记不同辐射源的脉冲序列，可见3 个辐射源均被检出。其中绿色线段对应的辐射源相位斜率差距大，使不同的相位直线未能合并为同一个辐射源。

图16 TOA-PH 二值图像

图17 霍夫线段检测结果

脉冲分选结果如表2 所示。根据分选结果，可见算法对频率固定辐射源分选效果较好，分选准确率可达90%以上，脉冲提取准确率高于85%，且分选性能基本不受PRI 调制类型影响。算法对频率捷变辐射源分选准确率和脉冲提取准确率较差，原因是捷变频辐射源脉冲序列散布在不同的频率聚类中，每个频段内脉冲数量相对较少，难以检出时间-相位直线特征。

表2 脉冲序列分选结果

4 结束语

针对旋转干涉仪雷达脉冲信号分选中的难点，对雷达脉冲序列信号相位随时间变化的规律进行了分析，提出了一种基于霍夫变换的脉冲方位分选方法。仿真实验表明，该方法能够实现对不同频率、方位辐射源信号的分选，且分选效果受PRI 调制方式影响小，鲁棒性较好。同时，该方法也存在一定问题，如对捷变频辐射源适应性较差、霍夫变换运算量大等，有待进一步研究和完善。