基于遗传算法的干扰态势下三维雷达网优化布站方法

周宇泰，徐 岳，李 宇，蒋国韬

（上海机电工程研究所，上海 201109）

0 引言

雷达组网布站在现代电子对抗中可以显著提高网内雷达的探测概率和生存能力，在面对日益加深的全方位全天时空天打击威胁时，扮演着至关重要的作用。然而该问题是典型的高维度非线性目标函数求解问题，一般的数学解析法或传统优化方法无法求解，需借助智能优化算法进行分析和求解。例如，郑贵文等通过模拟鸟群觅食行为而建立了一种基于粒子群算法的群体协作的雷达网优化部署方法，实现了可行解空间中雷达位置的寻优；连鲁军等提出了基于混合蛙跳算法的雷达组网优化部署方案，该方法模拟了自然界中青蛙按照族群分类进行思想传递寻找食物的过程，从而实现了全局寻优；蔡婧等还提出了基于文化遗传算法的雷达组网优化部署方法，该方法通过群体经验和行为知识获取存储等机制，指导了种群空间进化过程。除此之外，还有模拟退火算法、蚁群算法等其他机制求解复杂优化问题的算法，为解决雷达组网布站这一复杂问题提供了新的思路和手段。

然而，上述雷达布站过程都可以被认为是无干扰情况下的静态的二维布站方法。具体来讲，上述布站方法将雷达威力建模成理想的二维平面圆形。然而在现代电子对抗场景下，这种简单近似将使得雷达网在面对天顶攻击、超低空突防等专门针对时显得力不从心。同时，现代电子对抗中干扰机的使用也使得雷达威力形状被压缩、变形，进一步削弱了上述方法的实用性、可靠性。与此同时，在如今复杂对抗环境中，合理利用、正确理解对抗形势并迅速做出相应调整和部署成为了把握主动权的关键所在。

为弥补传统雷达布站方法在现代电子对抗场景下的劣势，本文提出了一种基于遗传算法的干扰态势下三维雷达网优化布站方法。该方法建立了干扰态势下对应空间雷达威力范围的模型，并基于该模型和遗传算法，着眼于统筹兼顾、合理分配、突出重点的雷达资源布站，实现了对要地区域的三维立体探测防护。

1 干扰态势下雷达组网优化部署原理

1.1 干扰态势下雷达威力三维建模

雷达通过接收目标对电磁波的反射（回波）实现对目标的探测，在三维空间内雷达能够有效探测到目标的最远边界所形成的闭合区域被称之为雷达的威力范围。在不考虑高度、地形等外部条件影响的理想情况下，雷达威力范围可以表示为

式中：为雷达发射的峰值功率；为雷达天线的发射增益；为雷达所使用的波长；为雷达散射截面积；为脉冲积累数；S为雷达接收机最小可检测信号功率。

当雷达未受到干扰时，S主要取决于雷达自身的噪声。当雷达受到干扰时，雷达通过天线主瓣指向目标，同时干扰机通过天线主瓣指向雷达。此时，干扰机的干扰能量从雷达天线的副瓣、背瓣进入雷达和目标回波信号同时进入雷达，从而对雷达威力实现压制。考虑到干扰信号需要对大于目标回波信号一定倍数才能形成干扰，则设干扰机进入雷达接收机的等效最小干扰信号功率为

式中：为干扰机的发射功率；为干扰机天线主瓣增益；为雷达接收机带宽；为干扰机发射带宽；为干扰机的干扰信号对雷达天线的极化损失；为雷达到干扰机的距离；为压制系数，即干扰机能够干扰雷达所需的最小干信比；()为雷达天线对干扰信号的接收增益修正系数，该系数是干扰信号入射角度的函数，与具体的雷达天线特性有关，其计算式为

式中：为雷达天线水平半功率波束宽度；为第一修正系数，对于高增益、波束较窄的天线，的取值范围为0.07至0.10，对于低增益、波束较宽的天线，的取值范围为0.04至0.06；为第二修正系数，即采用旁瓣对消技术时对于增益的修正，取值范围为0.01至0.10。

当存在多架干扰机时，雷达收到的干扰信号是所有干扰信号的叠加，即当存在多架干扰机时，收到的总等效干扰信号功率为

此时可以得到雷达的最大探测距离表示为

空间上的探测距离是雷达二维威力范围与垂直面天线方向图的函数。为了能够真实地反映垂直面上干扰机与雷达主瓣间的夹角对雷达探测威力的影响，雷达在三维空间中的探测威力可以表示为

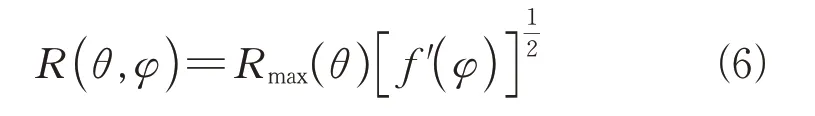
式中：为水平面上干扰机到雷达的连线同雷达主瓣中心线之间的夹角；()为雷达天线在垂直方向上的归一化方向函数，可以近似为

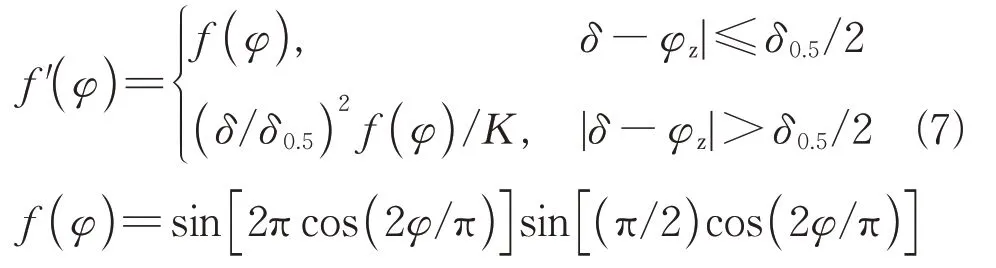
式中：为干扰机在雷达极坐标系下的俯仰角；为雷达天线的垂直波束宽度；为雷达天线在俯仰角上的波束指向；为增益修正系数。

上述分析指出，在遭遇干扰时雷达威力将发生显著变化。若雷达受到干扰时依旧按照未受到干扰时的理想情况进行布站，则将出现探测盲区，极易给非合作目标的侵扰留出可乘之机。此时如果能够在布站时得到干扰方向等信息，则可以有的放矢，建立雷达威力动态模型，从而更好地进行防护。

1.2 优化部署的目标函数

组网雷达优化部署的目的是充分发挥多雷达优势，提高雷达网的整体探测性能，因此本文重点从3个方面对雷达组网部署进行优化：考虑雷达网不同区域的覆盖侧重程度、要地的覆盖能力以及要地的覆盖重叠性。

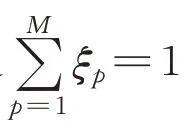
雷达网对于要地的覆盖能力可使用空间覆盖系数来表征雷达组网覆盖区域体积与责任区域体积之比。

式（6）指出，在雷达和干扰机参数确定的情况下，两者之间的距离、方位将影响雷达威力的形状和大小。因此，当雷达在不同的坐标位置进行部署时，雷达的威力范围将在三维空间内发生动态的变化，从而影响对于要地的覆盖结果。

当雷达网中的雷达布置在不同的坐标位置时，用S表征第部雷达威力在第个子区域三维范围内的覆盖体积。因此，空间覆盖系数可以表示为

为了提高对非合作目标的探测概率，可以使多部雷达的威力范围在要地区域形成覆盖。通常情况下，应有尽可能多的雷达覆盖要地区域，保障覆盖区域内雷达有一定的冗余度。实际情况中，两部雷达同时覆盖某一区域较为合理，更多雷达同时覆盖将造成雷达资源的浪费。

因此，使用来表示空间重叠覆盖系数以表征雷达网的覆盖重叠性，其定义为在要地区域内两部雷达重叠覆盖区域体积与三部雷达重叠覆盖区域体积的差占要地区域的比例。空间重叠覆盖系数表达式为

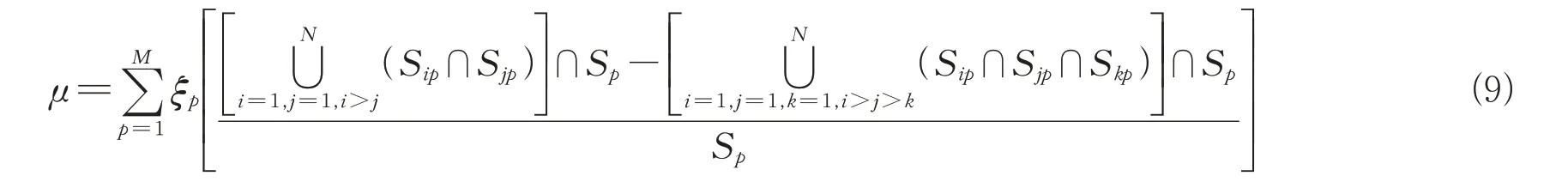
式中：S、S、S分别为第、、部雷达在第个子空间的探测体积；S∩S∩S为第、、部雷达在第个子空间的探测重叠体积。

在上述考量之下，优化部署的目标函数可以表述为+。由此，该雷达布站问题可对应地转换为如下数学优化模型：

即求一组含有个雷达坐标(，)，(，)，…，(x，y)的解，使得空间覆盖系数与空间重叠覆盖系数之和为最大值。

2 基于遗传算法的干扰态势下雷达网优化布站方法

遗传算法是受达尔文进化论的启发而形成的自适应搜索优化算法。该算法采用概率化的优化搜索方法，突破了传统优化算法中对于目标函数可导性、连续性等诸多方面的限制，具体过程如下。

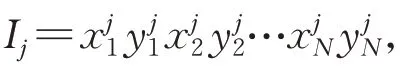
在初始种群生成阶段，确定初始群体规模后，可随机产生初始种群的个体。根据先验知识可知，在雷达进行布站时，应将雷达部署在要地区域附近，且雷达越靠近核心区，对于核心区的覆盖效果越好。因此可以以核心区中心为中心，依二维高斯分布产生随机的初始种群。

选择算子可以根据适者生存的原则选择下一代个体。在选择时，首先对种群内所有个体进行适应度评价，然后对个体进行选择。适应度较高的个体参与繁殖的次数更多，适应度较低的个体参与繁殖的次数更少，从而能够产生更加适应环境的后代。从优化问题求解的角度看，即能够产生适应度更高的后代，从而接近最优解或次优解。具体实行阶段，由式（10）可知个体的适应度函数为+。本文采用适应度比例方法进行选择：随机选择一个个体作为参与繁殖，被选中的概率与个体的适应度成正比。对于个体I，其适应度函数为ρ+μ，则个体I被选择的概率(I)可以表示为

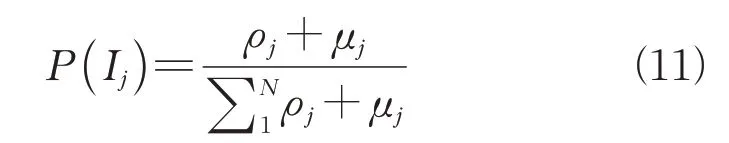
该方法使得在新种群中个体数目与原群体个体总数相同。

图1 交叉算子示意图Fig.1 Schematic diagram of crossover operator

变异算子是使算法跳出局部最优解并在全局范围内寻找最优解的一种保证。在给定变异率的情况下，随机产生一定数量的变异点。变异后的基因为产生的随机整数与变异点基因的求和。

算法终止条件可以根据需要进行设定，算法终止后最优个体即认为是一个最优解或准最优解。算法终止通常包含两种策略：一是在经过某次迭代之后，种群中最优个体的适应度+已经满足了覆盖率的需求，即可认为满足终止条件；二是迭代次数超过所规定的次数时，即可认为满足终止条件，此时最优个体即认为是一个最优解或准最优解。实际操作过程中选择其一即可。

算法总体输入输出框图如图2 所示，在输入所有待部署雷达参数、干扰机参数以及要地参数后，再经算法优化，可输出最优或次优雷达部署的坐标，以及在该情况下对于要地的覆盖结果，同时可以生成干扰态势下的雷达威力图以直观了解对抗态势。图3为优化部署算法流程。

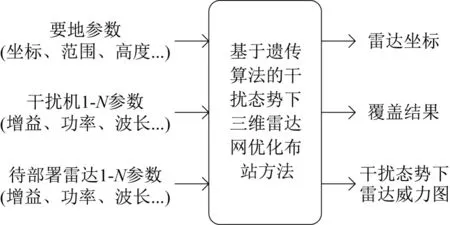
图2 算法总体输入输出框图Fig.2 Block diagram of the algorithm input and output

图3 优化部署算法流程Fig.3 Flowchart for optimal deployment algorithm

3 算例仿真与验证

首先验证所建立的干扰态势下雷达威力三维模型的正确性，对式（6）给出的雷达威力变化进行仿真。

图4（a）～（d）展示了某一干扰机逐渐接近雷达的过程中依照式（6）计算得到的雷达威力示意图的变化仿真结果，图中雷达威力由无干扰情况下雷达威力最远距离进行归一化。

从图4（a）中可以看出，在无干扰或干扰机距离很远的情况下，由于在水平方向上雷达的最大探测距离相同，雷达的威力范围呈现出顶部存在凹陷的规则椭球型；而在垂直方向上，由于天线的垂直方向图函数在俯仰角接近90°时会急剧减小，雷达的最大探测距离也随着天线垂直方向图的变化而变化，在顶部呈现出凹陷，即雷达的顶空盲区。从图4（b）中可以看出，在干扰机干扰方向上，雷达威力在干扰机逐渐接近的过程中出现一条裂缝，且伴随着干扰机的进一步接近，裂缝逐渐扩大，呈现出图4（c）所示的雷达威力形状。由于干扰机的更进一步接近，最终雷达威力范围进一步缩小，但雷达威力图形状不再发生变化。这是由于雷达旁瓣、背瓣等接受了干扰信号，从而使得雷达威力在未朝向干扰机的方向上也发生了减弱。上述雷达威力的变化过程与实际经验相符，验证了所建立模型的正确性。

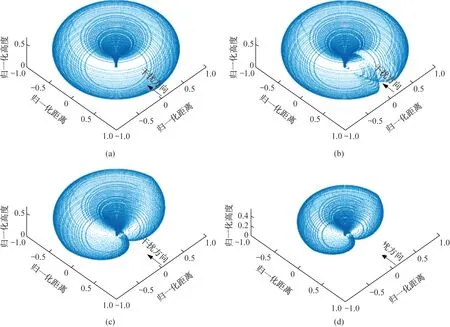
图4 归一化雷达威力示意图Fig.4 Diagram of normalized radar power coverage

从上述干扰机对雷达干扰的过程中可以看出，雷达威力范围会随干扰情况动态变化，这就使得在干扰来袭方向未知的情况下，原有的雷达布站方法很难做到对要地区域的准确覆盖，从而使得非合作目标在对要地区域进行侵扰时不能对其进行有效探测。如果此时考虑干扰情况下雷达威力的变化并据此动态布站，即可实现利用多部雷达相互协作、互为补充，从而充实探测空间范围的目的。

在验证所建立模型的正确性后，通过以下算例验证所提出的布站方法的有效性。想定如下待布站雷达场景作为优化布站方法的输入。干扰机参数为：坐标（500 km，750 km）、高度10 km处存在干扰机1架，对坐标（500 km，500 km）附近的雷达实行远距离支援干扰。要地参数为：在坐标（500 km，500 km）处划定高25 km、半径30 km的核心区，同时在核心区外围坐标（500 km，500 km）处划定高25 km、半径80 km的警戒区。同时，在干扰方向上存在非合作目标进入核心区的可能，因此，在干扰方向±15°范围内划定一级警戒区，在±30°范围内划定二级警戒区。整体场景如图5所示。

图5 想定雷达布站场景示意图Fig.5 Diagram of radar deployment scenario

基于上述遗传算法设计流程，在上述想定干扰场景下进行4 部雷达的布站，在空间中三维坐标搜索精度都设定为1 km。每部雷达的参数如下：=10W，=40 dB，=0.056 m，=16，=3 m，=1.6×10Hz，=5，=2，=5，=10，=290 K；并假设某型号干扰机参数如下：=10W，=30 dB，=2×10Hz，=0.5，=5，=5。由以上参数结合式（6）即可得到1部雷达在某一对应坐标下的威力范围。本算例中，遗传算法中的一个个体拥有4 部雷达，则根据上述过程即可得到4 部雷达的威力。在此基础上，利用式（8）和式（9）即可计算雷达在要地的空间覆盖系数及空间重叠覆盖系数，进而得到该个体对应的适应度函数+。本算例中，核心区、责任区、一级警戒区、二级警戒区的权重系数分别为空间覆盖系数=[0.18，0.09，0.18，0.09]，以及对于核心区、一级警戒区的空间重叠覆盖系数=[0.36，0.09]。遗传算法的迭代参数被设置为：种群规模为100个，最大迭代次数为200。

通过上述信息，结合雷达威力模型和遗传算法对4 部雷达进行布站，可以得到最终的雷达布站结果如图6（a）所示，图6（b）为雷达布站结果的俯视图。

上述布站结果实现了干扰情况下对核心区、责任区、一级警戒区、二级警戒区的85.27%、99.91%、83.70%和98.00%的单次空间覆盖率，对核心区、一级警戒区92.25%、26.52%的两次空间覆盖率；同时，显示了雷达受干扰时的三维探测威力，且能够根据干扰信息参数动态变化，构建了更加直观的雷达对抗仿真场景。图6（c）展示了使用相同参数时传统二维平面布站算法给出的优化结果在接受干扰时的雷达威力覆盖范围，该结果对核心区、责任区、一级警戒区、二级警戒区的单次空间覆盖率分别为74.57%、40.36%、89.55%和87.81%，对核心区、一级警戒区的两次空间覆盖率分别为48.52%、5.34%。对比传统的二维平面布站算法，本文所提出的算法显著提升了雷达威力在空间中的覆盖率，对核心区、责任区、一级警戒区、二级警戒区的单次空间覆盖率分别提升了10.70%、59.55%、－5.85%和10.19%，对核心区、一级警戒区的两次空间覆盖率分别提升了43.73%和21.18%。

图6 雷达布站结果示意图Fig.6 Result of radar deployment

从上述仿真结果中可以看出，本文所建立的干扰态势下动态变化的雷达威力模型更加真实地反映了干扰对于雷达威力的影响，且能够实现雷达对于要地区域统筹兼顾、重点突出的立体防护。

4 结束语

雷达布站时需要构建全方位、立体化、多层级防护网络的基础，然而传统雷达布站的静态二维布站方法已不再满足现代电子对抗的需要。本文提出了一种基于遗传算法的干扰态势下三维雷达网优化布站方法，实现了干扰态势下三维立体空间内的雷达布站，能够对要地区域实现统筹兼顾、合理分配、重点突出的探测效果，并能够将布站结果进行三维立体展示，从而更直观地显现了当前电子对抗态势。然而本方法还存在一定不足，评价因子的数量和维度需要进一步细化分析，例如对雷达间干扰、雷达威力衔接等评价因素的研究都能对雷达优化部署目标函数的全面性起到提升作用。