空中目标分布式ISAR成像仿真技术研究

陈春红，顾村锋，胡 俊，杨建超，吴 文

（1.南京理工大学电子工程与光电技术学院，江苏南京 210094；2.上海机电工程研究所，上海 201109）

0 引言

随着航空航天技术的快速发展，空中目标的探测、识别以及监视在未来空中攻防对抗中起着至关重要的作用。空中运动目标特性与作战方式的快速发展，特别是空中目标的多样性、变化性与动态性，对雷达的性能提出了新的挑战。分布式逆合成孔径雷达（inverse synthetic aperture radar，ISAR）成像雷达就是为了满足空中非合作特种军用目标探测新需求、弥补单一地面雷达探测能力不足、发挥多雷达体系优势、提升空中目标预警探测的能力、提高成像分辨率和可靠性、降低新型空中目标威胁的新型预警探测装备和方法。

传统ISAR 利用单个传感器对目标进行观测，目标图像通常在一个较小的角度范围内获取。然而，对于大多数目标，雷达观测角度的变化可能导致目标散射点雷达散射面积（radar cross section，RCS）的剧烈波动。因此，单站ISAR 的成像结果往往具有很强的角度依赖性，从而给目标识别带来了很大的困难。通过融合不同空间位置的传感器数据，分布式雷达系统具有解决上述问题的潜力，从而可以提供更完备的目标图像信息来进行目标识别。此外，对于一些特殊的情况，例如目标沿雷达视线运动，目标与雷达间的相对转动很小，单站ISAR 的成像分辨率就会很低，但分布式ISAR 可利用各站观测角度的差异获取成像所需转角。因此，研究分布式ISAR 成像技术具有非常重要的理论意义和应用价值。

分布式ISAR 成像技术的实现基础是对目标散射特性进行研究，主要有3 种途径：第一种是外场试验，但是对于空中目标而言，存在成本高、周期长、易受环境影响、样本量不足等问题；第二种是暗室测量，存在大目标测试困难、某些场景难以实现、周期长的问题；第三种是采用电磁仿真技术，这种方法成本低、周期短、可重复性强。借助商用电磁仿真软件，规避了复杂目标的散射点提取，可得到任意形状、任意姿态的目标特性，精度足够满足工程实践需求。

本文针对空中目标构建分布式ISAR 成像仿真系统，可以对各种空中目标进行大量、快速、低成本的成像技术验证。分布式ISAR 成像仿真不仅为分布式ISAR 系统设计提供有力的参考依据，还可以用于检验各种成像算法。目前已有一些关于ISAR 成像仿真的相关文献，但是对于分布式ISAR 成像仿真技术的研究还未见报道。因此，本文着重研究分布式ISAR成像仿真系统的关键技术及系统实现。

1 目标回波信号模拟

ISAR 成像仿真主要是在雷达成像的环境下，电磁模拟目标雷达回波数据，最后采用适当的成像算法得到目标的ISAR 像。电磁模拟雷达目标回波是雷达成像仿真的关键。

通常，ISAR 是指静止雷达对运动目标成像。现实中，雷达和目标之间的相对运动一般包含转动和平动。转动时，目标上的散射点沿纵向的位移使得回波产生多普勒频移，是成像的有用信息。而平动时，目标上各散射点回波的多普勒频率完全相同，无法用于成像，因此需要通过运动补偿去除。也就是说，理想情况下，通过运动补偿，可将任意运动转换为旋转运动，把ISAR 成像简化为转台成像。因此在仿真系统中，可假设目标为理想转动目标，且满足远场条件。由于运动是相对的，可看作雷达绕着目标转动。

ISAR 距离向高分辨率主要依靠发射足够宽带宽的信号实现，成像雷达主要有3 种类型的宽带发射信号：宽带LFM 信号、频率步进信号、载频跳变的窄带LFM 信号。本文模拟雷达回波时发射信号采用频率步进信号，设雷达发射信号载频为，带宽为，频点数为，则每个频点对应的频率为

式（1）的一系列频率所对应的信号称为雷达一组频率步进脉冲序列（即一次扫频）。

ISAR 方位向分辨率主要取决于成像角。假设目标固定，雷达绕着目标转动一个小角度，设雷达入射角为，雷达成像角为Δ，角度方向总采样次，则每个采样角所对应的角度值为

本文假设雷达在旋转过程中是步进的，即每旋转角度θ停顿一下，发射一组式（1）中的频率步进信号，计算得到一组目标回波，所有采样角对应的目标回波组合起来，即可构造出理想散射点目标的回波矩阵。采用CST 仿真软件可以快速准确地得出模型的远场散射特性，满足ISAR像仿真需要。

2 多角度ISAR信号融合方法

图1给出了多站ISAR成像示意图。

图1 多站ISAR成像示意图Fig.1 Schematic diagram of multi-station ISAR imaging

假设部雷达同时对目标进行ISAR 成像，且雷达间已完成空时频同步。忽略常数项的影响，完成平动补偿后，雷达1的基带回波信号可表示为

从而可以将雷达的回波信号表示为

由式（6）可以看到，雷达的回波信号可以映射至雷达1的空间谱域中，且雷达数据与雷达1数据的空间谱支撑区域不同，两个支撑区域相隔角度（如图2所示）。通常，将空间谱插值为均匀数据后，通过傅里叶逆变换即可将空间谱转换为目标图像。空间谱支撑区域越大，对应的空间分辨率越高，图像质量也就越高。

图2 多站ISAR回波信号空间谱Fig.2 Spatial spectrum of multi-station ISAR echo signal

对于单部雷达而言，其空间谱宽度受限于雷达的信号带宽和观测角度。若将两部或两部以上具有不同空间谱的雷达的回波信号拼接起来，再进行图像反演，即可增大回波信号在空间谱域上的支撑区域，进而可在不增加积累时间的前提下提高图像质量。同时，目标在较短的成像积累时间内可满足平稳运动的假设条件，从而大幅降低目标复杂运动对信号处理算法的影响。部雷达的回波信号进行融合成像的表达式为

式中：S为雷达的回波信号的空间谱支撑区域。

多角度融合ISAR成像算法流程如图3所示。首先，对回波数据进行距离压缩和距离向快速傅里叶变换（fast Fourier transform，FFT）处理后，快时间内的回波数据变换到距离频率域；接着，将各雷达站各脉冲的回波数据按照其相对目标的空间观测角度进行数据重拍；然后，将重拍后的二维回波数据映射至K-K波数平面，即可得到目标的二维空间谱，对目标谱进行距离向和方位向两次插值处理后可得到均匀的空间谱数据；最后对插值后的均匀二维空间谱进行两维快速傅里叶逆变换（inverse fast Fourier transform，IFFT）处理，得到融合后的目标ISAR图像。

图3 多角度ISAR融合成像步骤Fig.3 Multi-angle ISAR fusion imaging steps

3 分布式ISAR仿真系统

分布式ISAR 仿真系统主要由目标建模、目标回波模拟和成像融合3 部分组成，其工作流程如图4 所示。首先在CST 仿真软件中对几类典型目标建模；再根据雷达参数设置入射平面波模拟雷达发射信号，可仿真得到目标模型的散射系数；然后结合目标运动参数和背景参数，模拟目标回波信号；最后采用多角度ISAR融合成像算法得到目标ISAR图像。

图4 分布式ISAR成像仿真系统工作流程Fig.4 Workflow of distributed ISAR imaging simulation system

利用该仿真系统进行仿真时，需要对仿真约束条件进行探讨。

由雷达信号的基本理论可知，经脉冲压缩处理后，雷达的纵向分辨率为

式中：为电磁波传播速度；为雷达发射信号带宽。

由于雷达实际能达到的多普勒频率由相干积累时间决定，因此，雷达的理论横向分辨率为

式中：Δ=，为雷达成像积累角。

当目标转角变化较小时，一维距离像对雷达工作频率和目标运动扰动不敏感。但当目标转角的变化较大时，不同转角的一维距离像变化较大。对飞机之类的大目标，当飞行目标相对于雷达的转角变化较大时，各散射中心的相对距离也将产生变化，即产生距离抖动。

假设雷达距离分辨率为ΔR，则对翼展为的飞机，当目标方位姿态角变化量Δ＜ΔR/时，不会产生距离抖动；即使当目标转角的变化小到不足以产生距离抖动，散射中心相对距离变化也会产生相干斑（距离像的起伏），为避免这种起伏，要求目标方位姿态角变化Δ＜/（4）。另外，目标上相对目标运动的部位也会造成一维距离像的起伏。因此要求目标方位姿态角步进

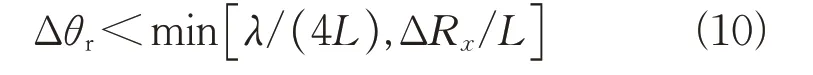
在一个扫频周期内，第个发射脉冲信号可写为

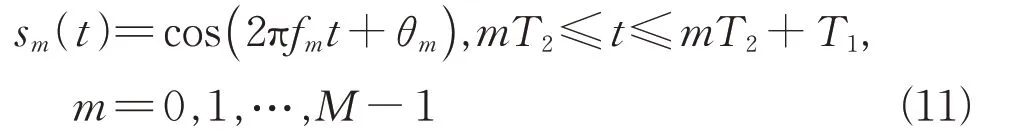
式中：θ为第个脉冲的初始相位；为每个脉冲持续时间；为脉冲周期，一般≥，两者相等时为频率步进信号。对目标采用多散射中心模型建模，则目标的后向散射回波为

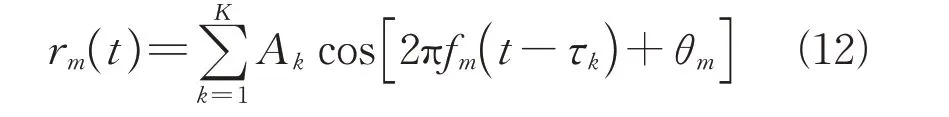
式中：s为第个回波分量的幅度。将式（13）离散化，有

式中：Δ为频率间隔。

式（14）表示一个多分量谐波模型，根据奈奎斯特采样定理，有不等式

即

4 隐身轰炸机成像仿真

以某隐身轰炸机为例，对其进行成像仿真。设定模拟目标回波的约束条件：距离分辨率和方位分辨率都要求不大于0.5 m，雷达工作在X波段低端，由式（8）和式（9），可计算出带宽≥300 MHz，转角Δ≥2°，因此可取带宽=400 MHz，转角Δ=2.3°。

对于某隐身轰炸机，其臂展（最大尺寸）约为60 m，根据式（16），可得频率间隔Δ≤1.25 MHz，可在400 MHz 范围内取512 个点；根据式（10），可得转角间隔Δ＜0.008 5°，因此可在2.3°转角范围内取271 个点，为了模拟多角度融合效果，仿真角度范围取10°。

在CST 仿真软件中，建立某隐身轰炸机模型，设置激励，可计算得到目标模型的ISAR 回波数据。

4.1 回波及RCS仿真

某隐身轰炸机模型如图5所示。

图5 某隐身轰炸机模型Fig.5 A stealth bomber model

图6给出了某隐身轰炸机模型的回波信号仿真结果。从图6中可知，该隐身轰炸机的回波非常小，比较明显的散射点很少，具有很好的隐身效果，不利于雷达的探测和成像。

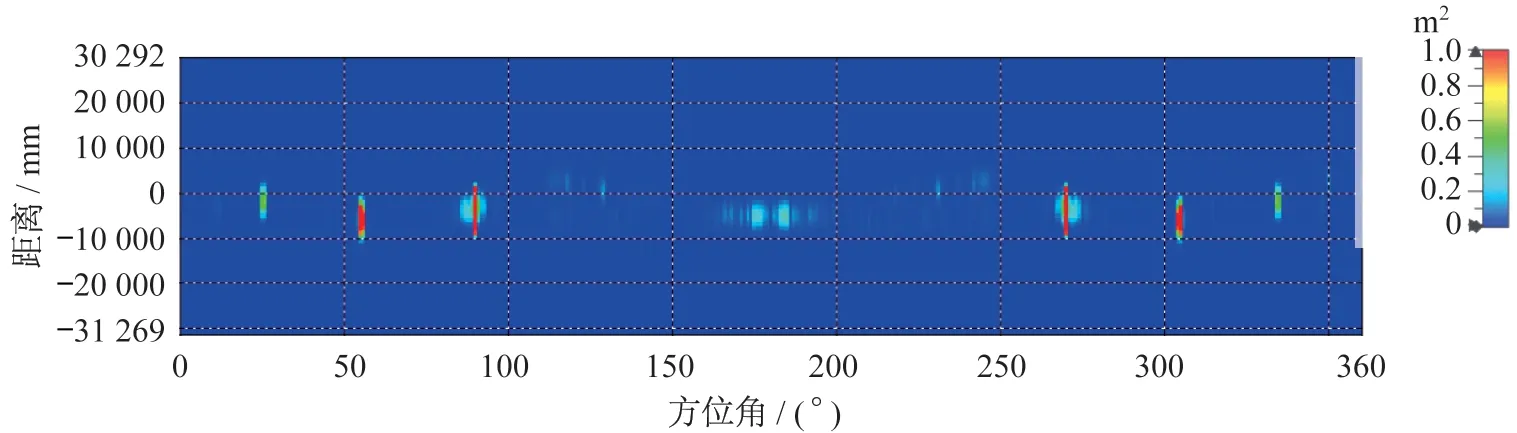
图6 θ=90°，φ=（0°～360°，步进1°）回波信号Fig.6 Echo signal at θ=90°，φ=（0°～360°，step 1°）

图7 为不同角度和不同极化条件下的单站RCS仿真结果。由图7 可知，水平极化时机头处的RCS 相对稍大，有一峰值点；俯仰方向入射角较大时，RCS将显著增大。此外，由于采用三角机翼，机翼处RCS较强；另一方面，由于采用了机身和机翼的融合结构，利用机翼将机身尽可能遮挡，故飞机侧向的RCS 得到了显著的缩减。

图7 单站远场RCS仿真结果Fig.7 Simulation results of single station far-field RCS

图8为双站RCS仿真结果（双站角度为180°）。由图8 可知，此时，RCS 的主瓣具有较大的值，并且主瓣集中于机尾方向，可见该隐身轰炸机将入射波散射到接近180°方向。此外，从图8 中还可以看出：在55°方向还有一个较窄的峰值，主要由三角机翼产生；小仰角入射时的回波峰值（约50 dB）显著强于大仰角入射时的回波峰值（约40 dB）。

图8 双站远场RCS仿真结果Fig.8 Simulation results of bistatic far-field RCS

图9 为不同俯仰角入射时的射线跟踪仿真结果。由图9 可知，当入射波对准机头或机尾（=0/180°），且接收与发射反向时，可能会有射线，其他情况几乎无射线。这进一步说明了该隐身轰炸机几乎将入射波散射到180°方向，造成接近于透明的效果。

并且，由图9可知，强散射点的分布与仰角有很大的关系。虽然入射波从机头处入射，但是当小仰角照射时，散射点不仅位置与该隐身轰炸机的轮廓线无关，且个数少、强度小；但是仰角增大时，虽然散射点位置还是与轮廓线无关，但是其个数明显增加，且强度也增加。

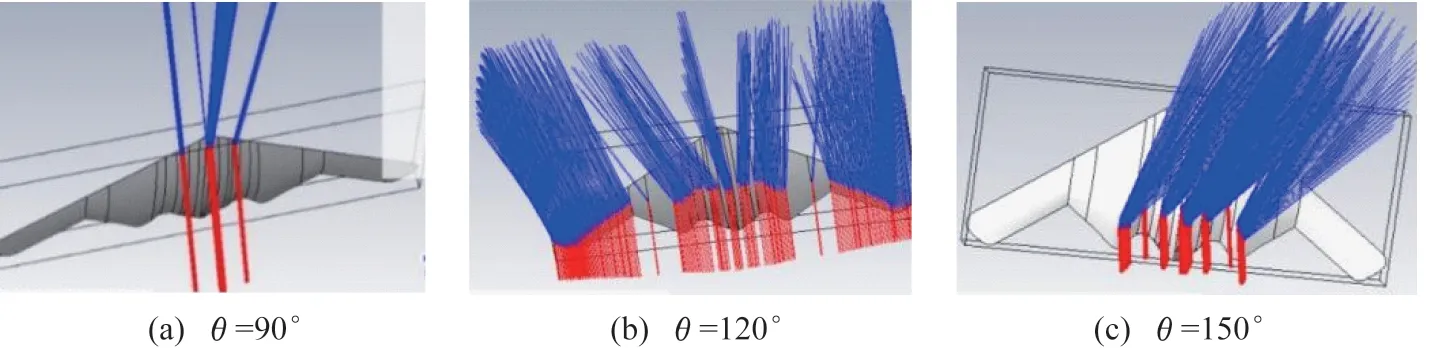
图9 双站射线跟踪Fig.9 Bistatic ray tracing

4.2 成像仿真

根据前面的分析可知，ISAR 成像算法有效的前提条件是：目标上的散射中心位置相对目标不发生变化，用CST 软件计算散射系数时，只要满足仿真约束条件，目标的散射中心发生变化对成像的影响很小。

下面利用CST 软件仿真单站回波信号对该隐身轰炸机的模型进行成像。

采用4 部雷达从空间不同角度对目标进行观测，雷达发射信号中心频率X波段低端，带宽400 MHz，布站间距2 km，目标距雷达50 km，每部雷达对目标的观测角度的差异约为2.3°，脉冲积累数为340。

图10（a）～（d）给出了各个角度的联合仿真ISAR像，由于该隐身轰炸机具有良好的隐身效果，明显的散射点非常少，仅机鼻和机翼尾部稍明显，在某些角度甚至只有5 个明显散射点，此时并不能得到轰炸机完整的轮廓信息。图10（e）给出了融合信号的成像结果，图10（f）为根据融合图像得到的轮廓图，可见多角度融合后可以得到目标的精细特征，虽然散射点不多，但是轮廓已经比较完整，与该目标的外形相当一致。

图10 某隐身轰炸机多站ISAR像Fig.10 Multi-station ISAR images of a stealth bomber

5 结束语

本文利用CST 仿真软件得到典型空中目标的复散射系数，与多角度ISAR 信号融合算法结合，构成分布式ISAR 成像仿真系统。并对某空中目标进行仿真，仿真结果表明，可得到任意角度的高精度ISAR 图像。分布式ISAR 成像仿真系统的实现，不仅解决了空中目标成像算法验证困难的问题，而且为空中非合作目标像数据库的建立提供了途径，为目标识别奠定基础。