基于均值漂移聚类的开关柜局部放电异常检测

黎阳羊，胡金磊，赖俊驹，王伟，杨帆

（1.广东电网有限责任公司清远供电局，广东 清远 511500；2.上海电力大学电气工程学院，上海 200090）

随着我国电网的不断发展，电力系统对电力设备的运行可靠性要求也越来越高，对电力设备的状态检测、评价与运维有着更高的要求[1-3]。目前，开关柜的评价方法主要有两种，一种是基于模糊综合、D-S论据（dempster-shafer evidential theory）等状态评价方法[4-6]，适用于开关柜停电检修时对开关柜进行全面细致的评估，包括了从目测柜体状态、表记状态、内部部件测试等方面提取特征量，在实际检修中停电检修的周期较长；另一种是通过聚类算法等机器学习算法在开关柜常规的带电检修中，对开关柜的局部放电程度进行评估[7-8]。该方法主要适用于开关柜的带电检修，实际检修中带电检修的周期远小于停电检修周期。目前现有文献普遍未对开关柜局部放电的检测机理进行全面的分析和研究，缺乏从检测机理入手构建开关柜的局部放电多维特征量。

开关柜的带电检测方法包括暂态对地电压（transient earth voltages，TEV）检测法和超声检测法，TEV的检测原理是检测放电点从柜体金属表面的断开处或者缝隙处随机散射的电磁信号，超声检测是检测局部放电活动中的声波辐射信号[9]。IEEE的指导准则中指出由于型号不一致、结构复杂、背景噪声以及不同检测传感器厂商的量化信号方式不同等原因，缺乏对开关柜绝缘状态进行全面的数据信息挖掘分析，单一的柜体检测难以对评估开关柜的局部放电的大小、劣化程度做出合理量化[10]。本文提出了一种全面的开关柜局部放电程度的状态评估技术。根据日常巡检中柜体前、后面的上、中、下6个检测点的TEV以及超声数据[11]，结合机理分析，引入检测数据的离散度、平均距离百分比、集中度以及最大波动率等指标量化开关柜的局部放电程度。

此外，本文对日常对各地区的各开闭所、环网柜以及分支箱的数据进行调研，局部放电异常的样本数据多为小规模离群异常数据。如文献[7]中某变电站绝缘状态异常的开关柜仅占总数的6.82%。文中所提出的基于距离的均值聚类算法，当异常点偏移正常样本较大且比例较少，其鲁棒性较差。而均值漂移聚类是基于滑动窗口的算法，其目的找到绝缘状态特征量所处的密集区域，不受异常点的影响。由于每次滑动的窗口随着样本点的变化，其偏移量对均值偏移向量的贡献也不同。因此，本文通过高斯核函数自动量化均值漂移方向与大小，并基于文献[12-13]对绝缘状态进行划分。同时为了自动判别聚类算法所划分的簇是否为异常点，本文给定簇标签隶属度函数判断该簇是否为异常点[14]。

综上，本文依据柜体和环境参数及局部放电检测数据的离散度、平均距离百分比、集中度以及最大波动率4个指标全面量化开关柜绝缘劣化状态，同时建立多维特征库。采用基于高斯核函数的自动寻参均值漂移聚类算法对绝缘状态进行划分，并给定簇标签隶属度函数自动判断该簇是否为异常点，由此实现开关柜的异常检测。

1 开关柜局部放电的波动性与局部放电异常检测流程

参考国家电网公司的Q/GDW645—2011标准《配网设备状态评价导则》，从柜体TEV和超声局部放电检测评估开关柜的局部放电程度。局部放电的检测机理如图1所示，假设D为放电源，即当D处产生局部放电时，会产生散射电磁波信号的现象，TEV主要检测其从开关柜缝隙发出的电磁波，而开关柜的柜体是密闭的金属外壳，电磁信号无法穿透，因此测量局部放电异常的随机性比较高。结合如表1所示的日常各地区的各开闭所、环网柜以及分支箱的带电检测样本报告统计中典型的带电检测局放异常数据（通常以对数单位“dB”来表示放电强度）。异常数据具有较强的波动性——主要体现在整体偏高或局部偏高。对于超声信号，同样存在漫散射问题。

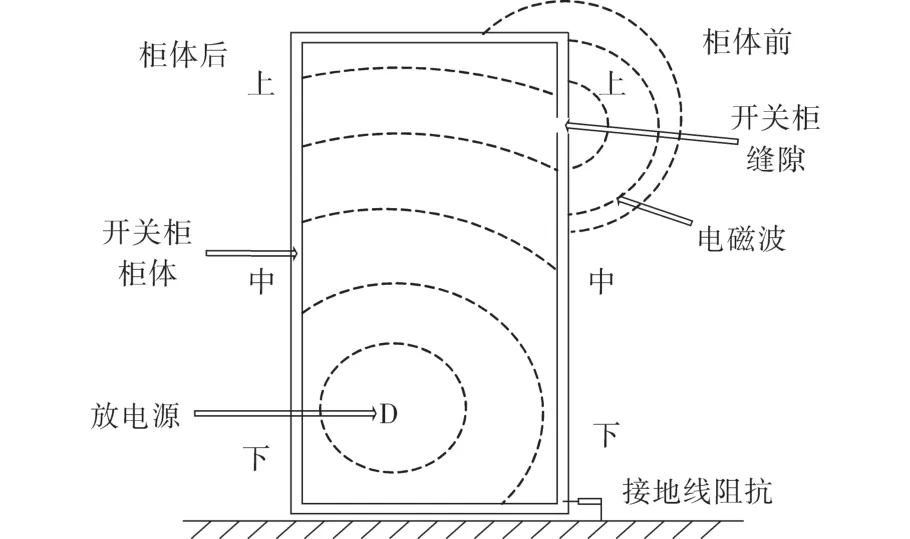
图1 局部放电的检测技术机理Fig.1 Detection of partial discharge mechanism

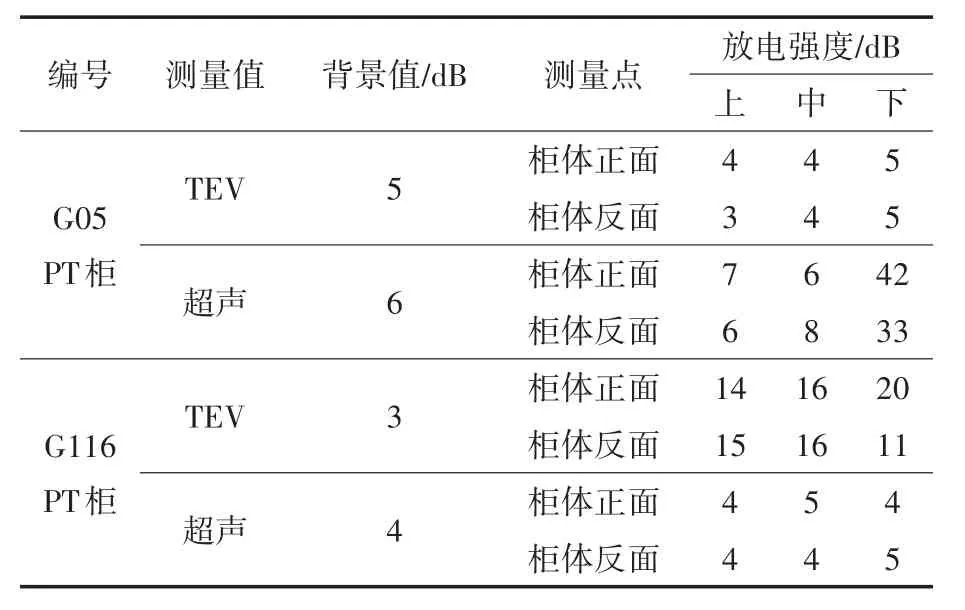
表1 典型的带电检测局放异常数据Tab.1 Classical online detection abnormal data

本文提出检测柜体前、后面的上、中、下共计6个检测点的离散度、集中度以及最大波动率量化开关柜的局部放电异常的情况。其中，通过离散度能反映开关柜绝缘状态数据的离散情况；平均距离百分比反映数据的偏移情况；集中度反映样本所处的中间水平；最大波动率反映样本数据的离差情况。

对多维度的开关柜特征量进行绝缘状态异常检测时，开关柜的原始绝缘状态样本数据劣化程度极少，通过全面的波动性量化将提高均值漂移聚类对异常点识别的鲁棒性。在均值漂移聚类算法中，首先可以确定处于密度大的样本点所处的类别，即聚类的簇，再对异常点进行逐步搜索。开关柜绝缘状态数据集的形状是未知的，而均值漂移聚类可以对任意形状的数据集进行聚类。K均值聚类算法对小规模的异常样本点识别能力较弱。

如图2所示，均值漂移聚类算法选取初始中心点与半径为R的滑动窗口朝向密度大的聚类点进行漂移聚类，每次窗口滑动的方向和大小为向量Mh，初始点加Mh得出下一中心点，对其进行迭代计算，直至滑动窗口的偏移量收敛。该算法对沿密度最大的方向自动搜索，不需要人为设定算法的聚类个数。此外，均值漂移聚类结果没有偏倚，由于是遍历整个样本点并进行以半径为R的圆形自动搜索，初始聚类中心的位置对聚类结果的影响较小。相对的，K均值聚类算法对初始值非常敏感。

图2 均值漂移聚类示意图Fig.2 Diagram of mean-shift cluster

2 基于波动性指标的开关柜局放多维特征量数据库

2.1 开关柜绝缘状态波动性指标

2.1.1 减少开关柜背景值干扰

开关柜的带电检测数据包括6个检测点的TEV、超声的幅值检测量以及TEV和超声的背景值。首先计算TEV以及超声的幅值偏差量：

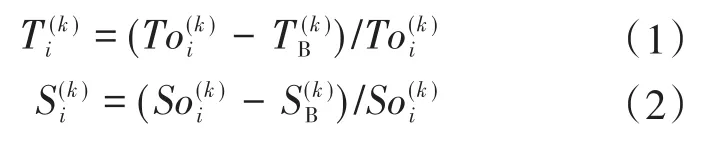
2.1.2 偏差量的惩罚函数

为了克服数据中含有负数或者零所带来的数据爆炸的问题——最大波动率不能为零，本文对偏差量引入惩罚项，使得整体的数据全部大于零，计算公式如下：

2.1.3 离散度

离散度能够反映开关柜局部放电检测数据的波动情况，分别对6个检测点的TEV和超声检测偏差量求离散程度。TEV的离散度如下式所示：

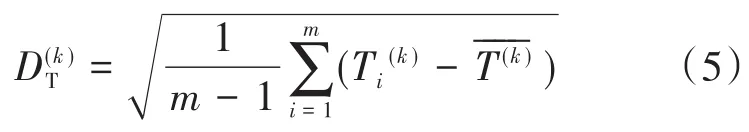
式中：m为数据点的数量为TEV幅值偏差量；为该台开关柜所有检测点数据偏差量的均值；为开关柜TEV检测数据偏差量的离散度。

同理，超声的离散度计算式如下式：

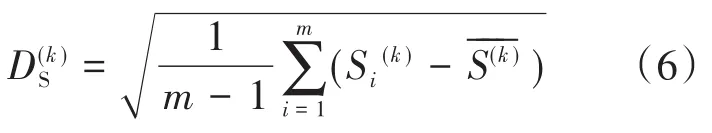
2.1.4 平均距离百分比

平均距离百分比为该台开关柜所有检测数据距离中心点的距离与均值之比，通过平均距离百分比揭示开关柜绝缘检测数据整体变动的程度，如下式所示：

2.1.5 集中度

集中度可以反映样本中数据的集中情况，通过6个测量的中数与众数之和的均值反映样本的整体情况。众数主要是对重复出现的数据进行记录；中数则与数据的排列位置有关，中数不受极大或极小值影响，通过观察中数可以找出开关柜的整体局部放电偏高的情况，当集中度越高时，局部放电状态越严重。其计算公式如下式：

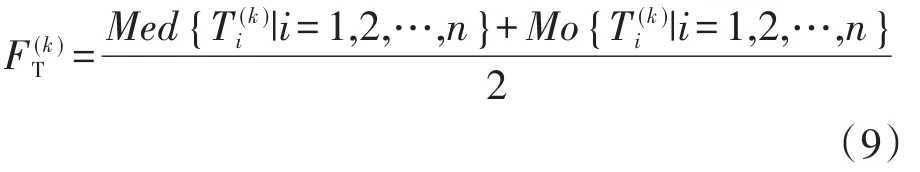
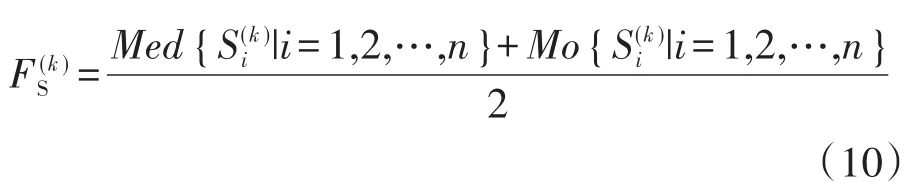
2.1.6 最大波动率

最大波动率能够量化开关柜局放程度的最大波动情况，区分数据的离差程度，反映数据区间跨度，如下式所示：

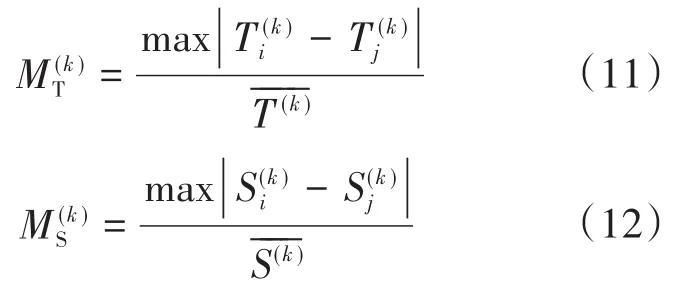
2.2 多维特征数据库

依据式（5）～式（12）的各台开关柜特征量的计算结果，开关柜的多维特征数据库可建立为

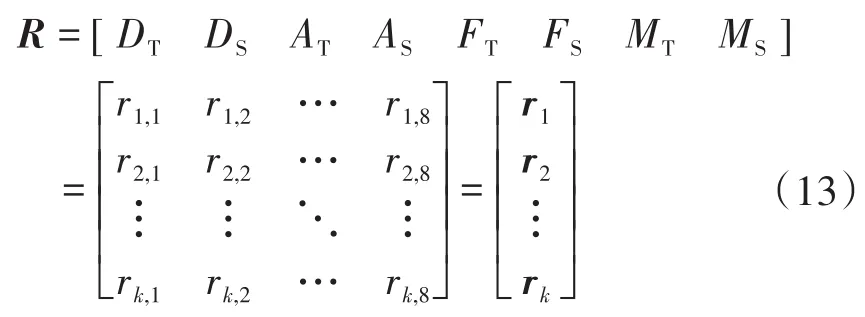
式中：R为开关柜的多维特征数据库；ri（i=1，2，…，k）为各台开关柜的特征量，例如rk,8代表第k个开关柜的第8个特征。

对所处理的特征数据进行z-score标准化，消除数据数量级之间的差异。

3 基于均值漂移聚类的绝缘状态异常检测法

均值漂移聚类是基于滑动窗口的算法，其目的是找到绝缘状态特征量所处的密集区域。它的目标是定位每类的中心点，通过将中心点的候选点更新为滑动窗口内点的均值来完成。然后消除近似重复，形成最终的中心点集及其相应的组。

对于给定的d维度空间Rd中的样本点ri（i=1，2，…，k），半径为Sh的高维球区域，其mean-shift向量的基本形式为

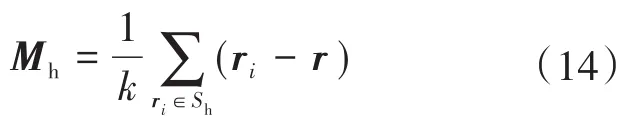
其中，r为任意选取的初始算法样本中心点，则在第t个中心点的漂移为

遍历高维球区域内所有的向量，求出meanshift向量，此时该向量称为均值漂移向量。因此，对于mean-shift均值漂移算法，通过算出当前点的漂移均值并进行迭代计算，并以漂移均值为新的起始点，直到其收敛为止。

在mean-shift算法中引入核函数使得随着样本与被偏移点的距离不同，其偏移量对均值偏移向量的贡献也不同。因此引入高斯核函数量化偏移度，点r的核密度函数估计为

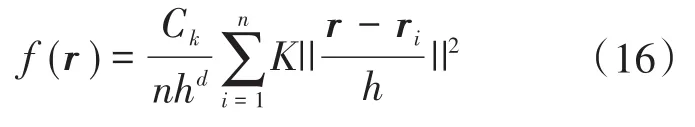
式中：Ck为常量；K为核函数；h为核宽。

对式（16）求导，寻找局部密度极大点：

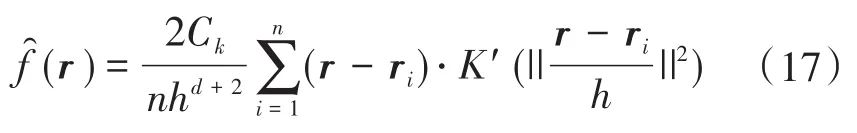
令g(r)=-K′(r)，式（17）可以表示为

其中

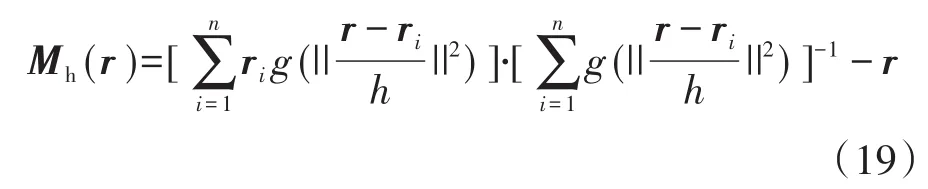
式（19）为基于高斯核函数的均值漂移向量。

在采用均值漂移聚类算法时，其聚类后的结果呈现出绝缘状态劣化程度差的时候样本点极少，个别情况下，单一的样本点是一个独立的簇。而处于平稳运行下的开关柜数据极多。

依据开关柜绝缘状态标签从优秀到异常会急剧减少的特性，本文采用如图3所示的簇标签隶属度函数，隶属度函数为等间隔函数，并依据等间隔制定从优秀到异常5个标签集。通过隶属度函数，找出样本点所在簇的标签。簇内样本点密度定义为

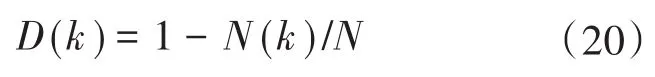
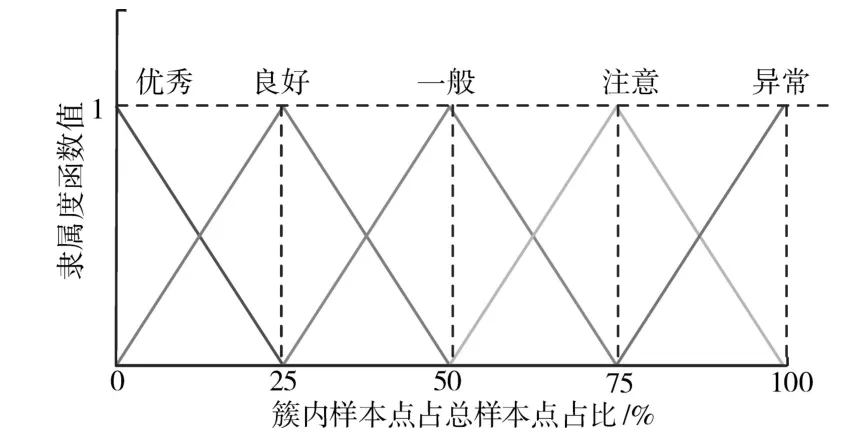
图3 簇标签隶属度Fig.3 Membership function of cluster label

式中：D（k）为第k个簇的样本密度；N（k）为第k个簇的样本点个数；N为总样本点个数。

综上，本文流程图如图4所示。

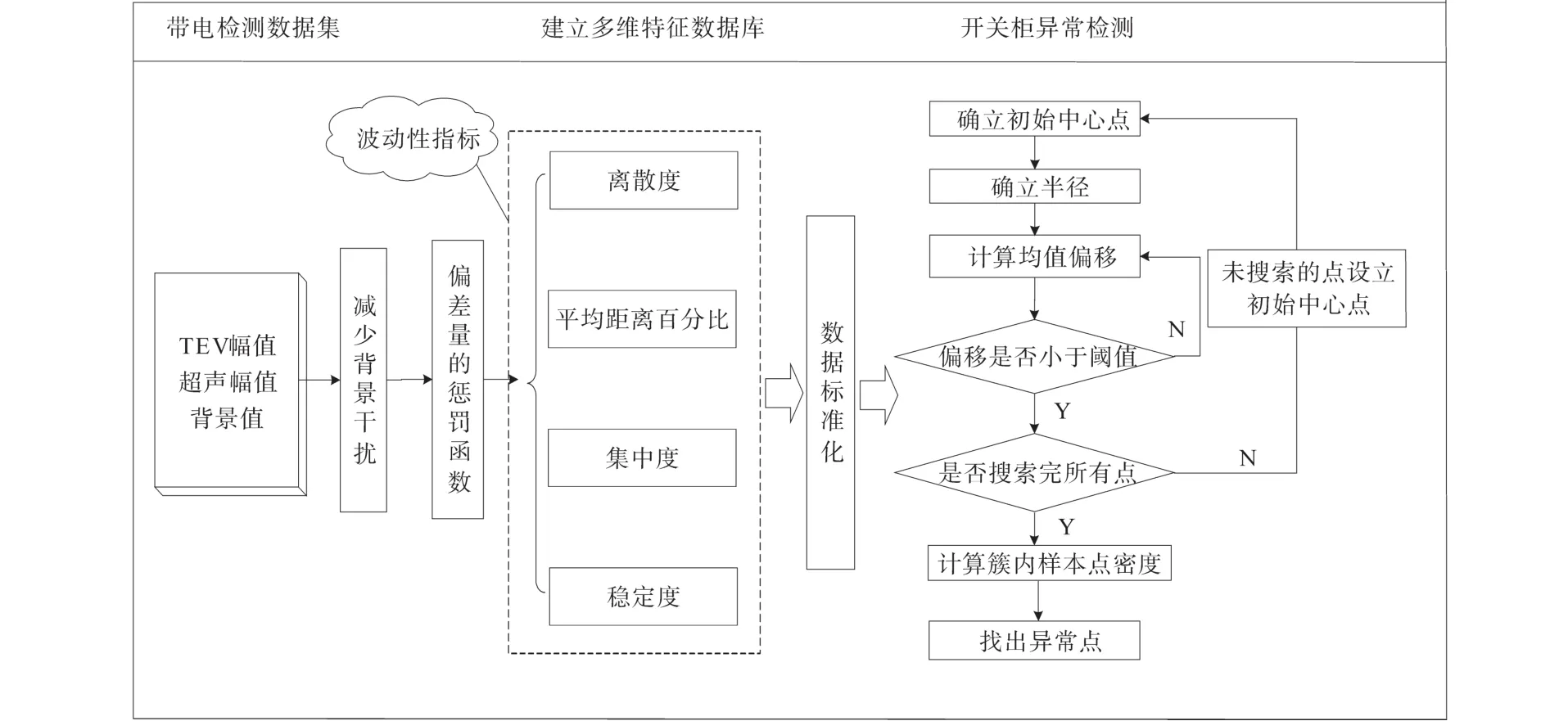
图4 开关柜绝缘状态异常检测流程图Fig.4 Switchgear insulation condition anomaly identification flow char

4 案例分析

选用某地变电站现场设备检测报告共计299组10 kV高压开关柜带电检测实测数据作为数据集，对上述算例采用实例分析。带电检测数据包括开关柜前、后面的上、中、下6个检测点的TEV和超声检测数据、背景噪声数据。案例分析主要包括了两方面：

1）本文基于所提出的波动性与均值漂移聚类，把未经过波动性处理与均值漂移聚类相对比，分别与专家根据《配网设备状态评价导则》对开关柜局部放电的评估结果对比，计算局部放电异常检测的准确率；

2）波动性处理后的K均值聚类算法与均值漂移聚类算法相对比，与专家根据《配网设备状态评价导则》对开关柜局部放电的评估结果对比，计算局部放电异常检测的准确率。

4.1 绝缘状态异常检测结果

应用局部放电多维特征量的构建方法，建立如式（13）的开关柜绝缘状态多维样本特征数据库R，并对数据库进行标准化预处理。通过均值漂移聚类算法，对开关柜的绝缘状态进行均值漂移聚类划分，聚类中心点如表2所示，各簇之间中心点划分明确。

表2 基于均值漂移聚类算法的开关柜绝缘状态聚类中心点Tab.2 The switchgear insulation condition cluster centers with mean-shift clustering algorithm

根据图2所示的簇标签隶属度函数计算所得的各类别标签如表3所示。

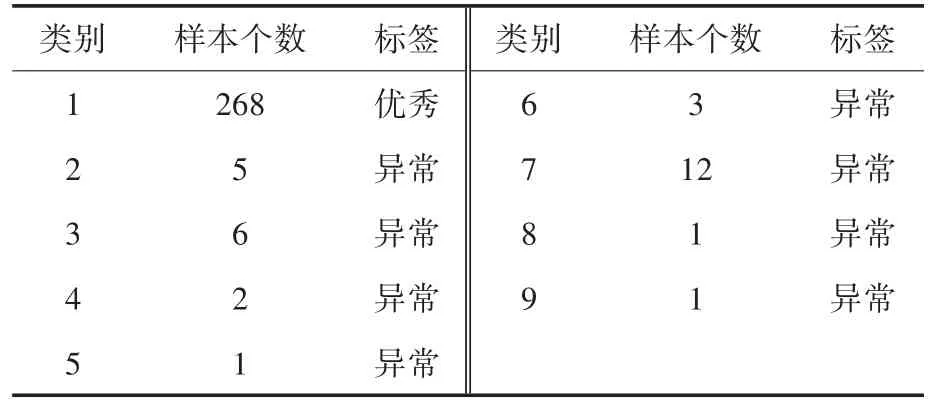
表3 均值漂移聚类算法簇内样本点个数Tab.3 The number of sample points under different clusters with mean-shift cluster

类别1的标签个数占样本总数的绝大多数，通过簇标签隶属度函数可得：所处于该簇的开关柜的绝缘状态等级为优秀，该簇下的开关柜未有明显的局部放电现象，可按照正常检测周期进行带电检测。而类别2～类别9中，绝缘状态的样本点的个数较少，存在着绝缘状态劣化的现象，建议运维人员加强关注缩短带电检测周期。

因此，基于表2以及漂移聚类的结果，其绝缘状态异常检测结果如图5所示。

图5 基于均值漂移聚类的开关柜局部放电异常检测结果Fig.5 Switchgear insulation condition anomaly identification results with mean-shift cluster

4.2 与其他方法比较的绝缘状态异常检测结果

分别对未经过波动性处理与经过波动性处理的开关柜带电检测数据进行绝缘状态异常检测。未经波动性处理的绝缘状态异常检测准确率为92.64%，处理后的准确率提升到了97.99%，可见波动性指标能更全面地量化开关柜的局部放电情况，切实有效地提升开关柜绝缘状态异常检测的准确率。

采用基于欧式距离的K均值聚类对绝缘状态进行异常检测，其不同K值下的准确率如表4所示，当K=8，此时准确率最高。但由于部分特征量离群度大，且K均值聚类对异常点的鲁棒性较差，导致其准确率与均值漂移聚类有一定的差距。其聚类中心点如表5所示。基于K均值聚类算法的样本中心点划分不够明确，对异常值较敏感，导致如类别1与类别3聚类中心点的划分不明确，出现中心点偏移的情况。且K由于需要人为提前指定使得判定是否为异常点较为困难。

表4 K均值聚类在不同簇下的状态评价准确率Tab.4 State evaluation accuracy of K-means clustering under different clusters

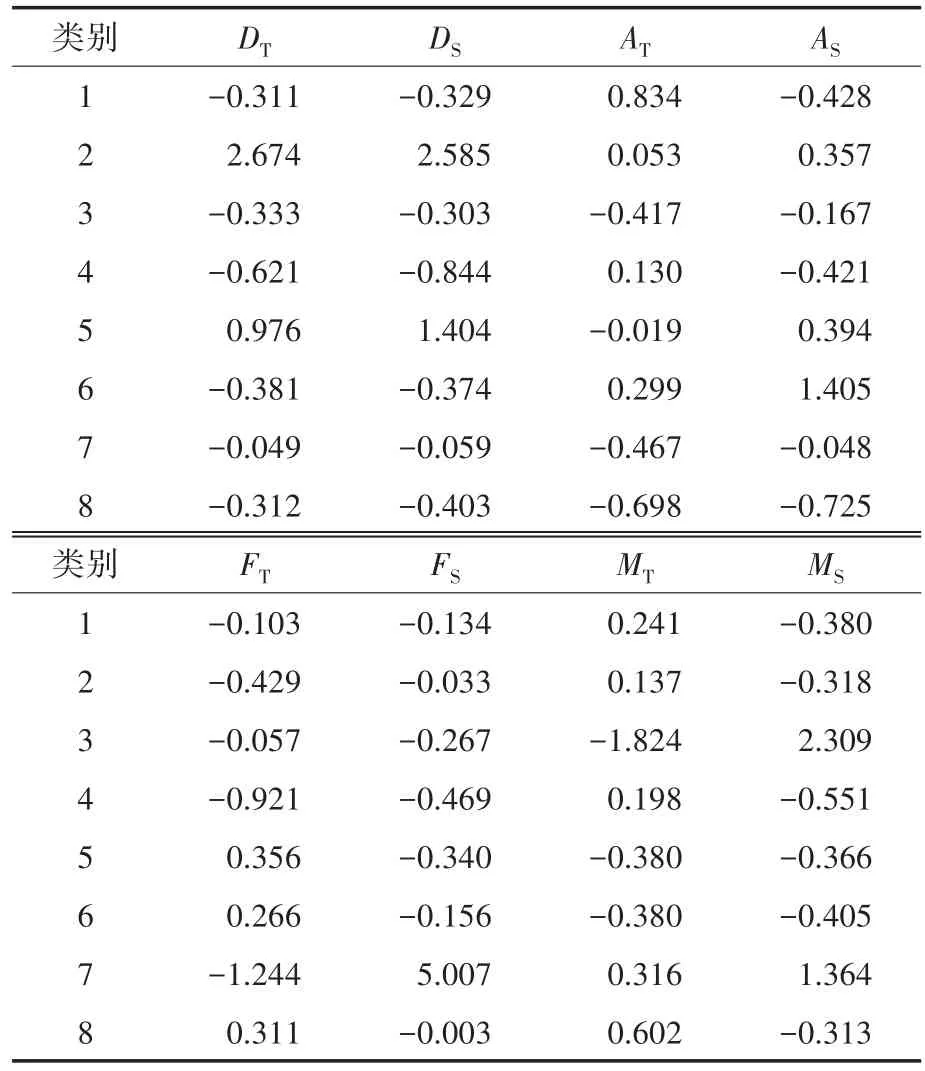
表5 基于K均值聚类算法的绝缘状态聚类中心点Tab.5 The switchgear insulation condition cluster centers with K-means clustering algorithm

综上所述，通过波动性处理，能够全面地反映开关柜绝缘状态。此外开关柜的绝缘状态异常点离群度较大，通过均值漂移聚类能避免异常点过大所导致的聚类中心点偏移的情况。

5 结论

1）本文所提的波动性指标能够反映对开关柜整体放电的突变程度。研究结果表明，通过波动性处理后的绝缘状态特征量能有效提升开关柜绝缘状态异常检测的准确率。

2）通过基于高斯核函数的自动寻参均值漂移聚类算法对绝缘状态进行划分，并给定簇标签隶属度函数自动判断该簇是否为异常点，能有效实现开关柜的异常检测。仿真案例表明所提方法对异常点有较好的鲁棒性，提高开关柜绝缘状态异常检测的准确率。