电力电子虚拟调相机

刘涛，蔡旭，孙国歧，魏晓宾，曹云峰，张玲艳

（上海交通大学风力发电研究中心，上海 200240）

随着新能源和电力电子技术的发展，电网中具有旋转惯量的机械装置逐步被低惯量的电力电子装置替代，使得系统的惯量逐年降低[1]。

在无功补偿方面的应用，传统方法是使用调相机等机械结构，但其体积较大，灵活度不高。随着电力电子技术的发展，静止无功补偿器（SVG）逐渐替代了传统的调相机。随着SVG技术的成熟[2]，装置投运逐年增加，容量和电压等级越来越大。

SVG最大的优点是响应快，可以实现动态补偿[3]，然而相比于传统的调相机，几乎没有惯性，当系统出现扰动或者电能供需不平衡时，无法像调相机那样，利用储存在转子的动能来阻尼电网频率的波动。

SVG的技术已相对成熟，目前针对SVG的研究主要集中在无功补偿能力提升[4-6]、主电路系统的稳定性[7-8]以及电网故障穿越[9-11]方面，这些研究均未考虑到SVG相对于传统调相机缺少惯量的缺陷。如何使SVG具备惯量响应能力，支撑高比例新能源电力系统的稳定运行具有现实意义。

本文提出一种电力电子虚拟调相机的概念设计，给出了控制策略和设计方法，可模拟调相机的功能，依据上级指令提供无功功率，或者针对电网电压进行无功补偿，维持电压稳定。当系统频率波动时，虚拟惯量响应阻尼电网频率波动。基于PSCAD/EMTDC构建了83 kW的虚拟调相机仿真系统，仿真分析结果表明，与SVG相比，电力电子虚拟调相机不仅可提供无功补偿，还具有惯量响应阻尼电网频率波动的能力。

1 虚拟调相机的拓扑结构

为了在短时间内提供高倍率有功电流，该系统中的储能模块选择超级电容器。由于超级电容器的电压随着有功功率的吸收或者发出会大幅度变化，需要在储能模块和直流侧电容间设计接口模块，保证系统的正常运行；同时，需要设计不同的主电路拓扑以满足系统电压等级以及容量的需求。

1.1 超级电容器的接口

在大功率应用场合下，由于受到磁性材料的限制，隔离性DC/DC双向变换技术难以采用，设计Buck/Boost变换器作为超级电容器接口，如图1a所示。

隔离式DC/DC是在非隔离式的基础上，加上高频变压器实现隔离。隔离型半桥双向变流器如图1b所示，可实现解耦，但对支撑电压要求较高，适合中等容量要求。

图1 双向变流器拓扑Fig.1 Bidirectional converter topology

1.2 主电路拓扑

普通的三相两电平是低压配电网中最常用的拓扑结构，如图2a所示，设计的三相两电平结构连接超级电容器模块，适用于电压等级较小的系统。

然而，在高压系统中，普通的三相两电平结构无法适用。如图2b所示，级联多电平系统直挂高压电网，无需工频变压器，从而相比传统拓扑结构具有更高的效率。

由于电力电子调相机提供暂态的惯量支撑，容量配置相比于传统的级联链式储能较小，设计如图2c的拓扑结构，将三相桥串联在级联拓扑中，以满足小容量、高电压的系统需求。

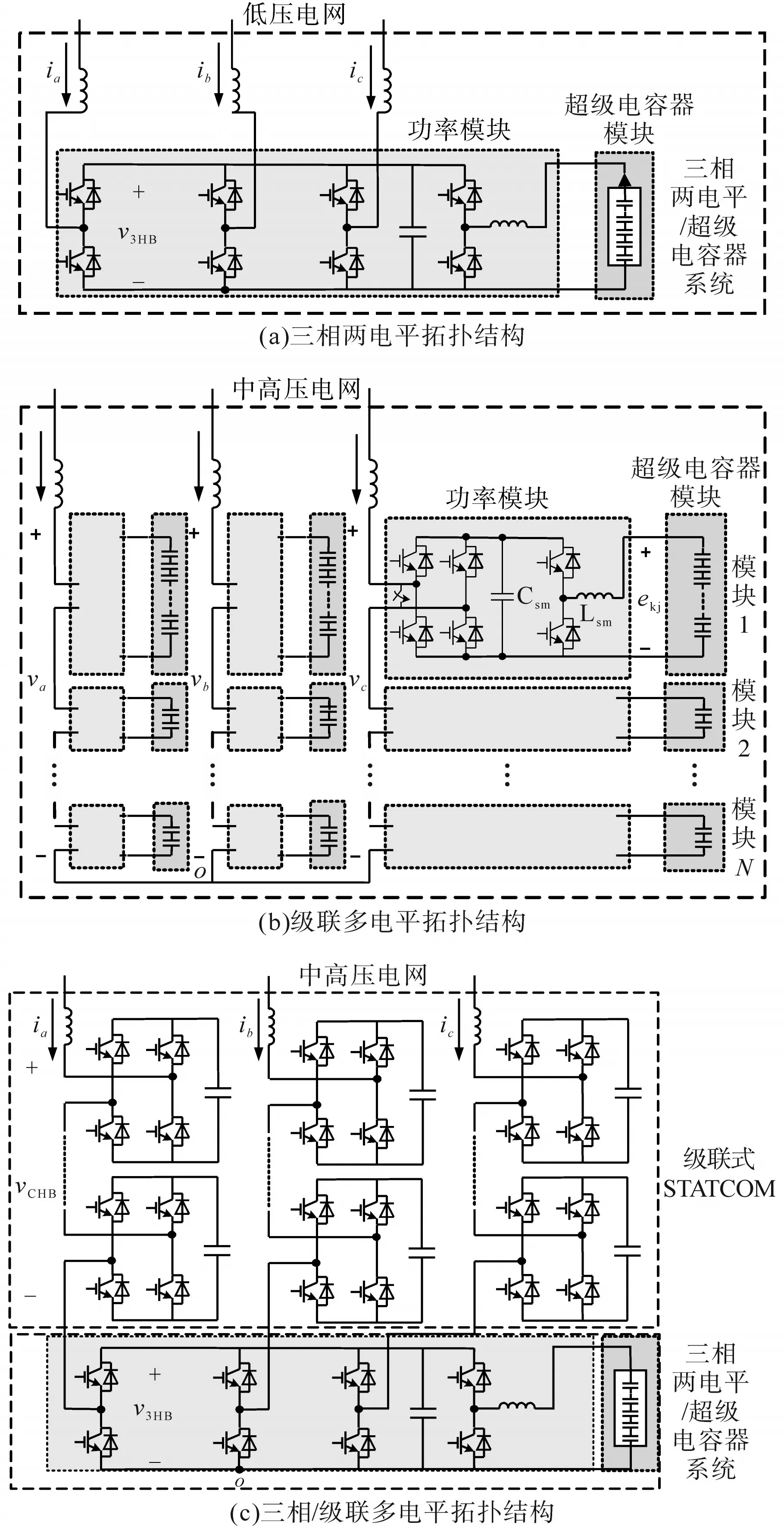
图2 主电路拓扑Fig.2 Main circuit topology

2 虚拟调相机的储能环节

2.1 储能配置

为了优化储能配置，提高储能配置的经济性，减小成本，需要进行合理的储能计算。首先分析传统调相机的能量模型以模拟传统调相机的惯量响应。

针对传统调相机，假设极对数为1，转动惯量为J，转子机械角速度Ω等于转子电角速度ωr，则调相机转动的动能Wk为

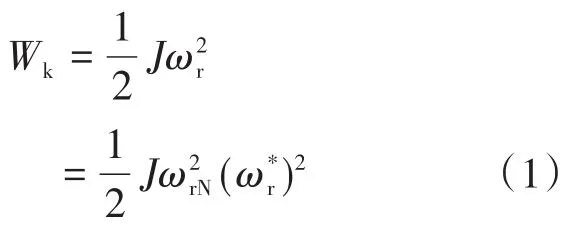
式中：ωrN为转子额定转速为转速的标幺值。

定义转子惯性时间常数为Tj、转子额定转矩为Tm、额定功率为PN，由于Tj的物理意义为转子从停顿状态加速到额定状态所经过的时间，则调相机转动的额定动能WkN为

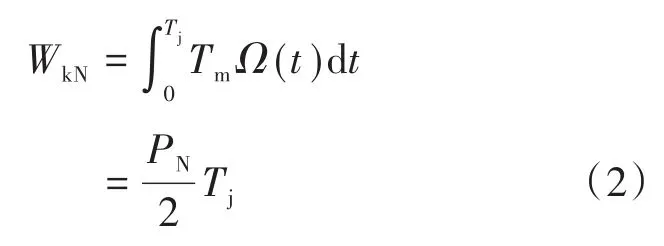
由于转速变化的限制，提供的能量仅仅是总机械动能的一部分。假设频率波动最大的标幺值为δ，联立式（1）和式（2），则调相机提供的动能ΔW为

为了保证系统的稳定，提供一定的能量裕度，假设裕度为λ（λ＞1），最终的储能配置的能量为ESC，联立式（2）和式（3），得：

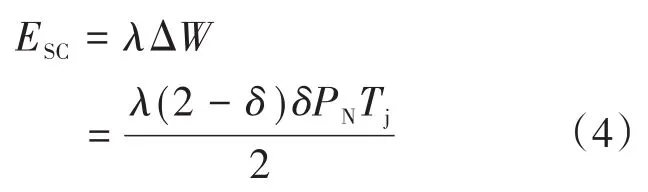
2.2 参数设计

超级电容器的电压会受到系统电压和拓扑结构的限制，其大小需要在一个合理的范围波动。当超级电容器电压过小时，会影响变换器的效率；电压过大时，会影响电容器本身介质的稳定性。假设最大电压的标幺值为μmax，最小电压的标幺值为μmin，额定电压为UN，电容为C，则超级电容器可用的能量ESC为

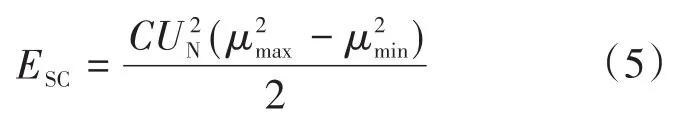
联立式（4）和式（5），得：

由于超级电容器是由多个电容单体串并联而成，假设一个单体的额定电压为usc，电容为Csc，且有m个串联、n个并联而成，则可以计算出超级电容器的串、并联参数如下：

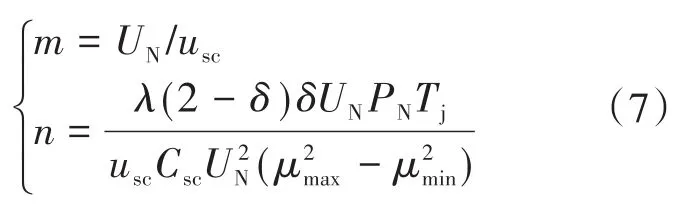
3 虚拟调相机的控制策略

电力电子调相机的控制策略主要由两部分组成，包括DC/DC双向变流器控制和DC/AC变流器控制。其中，DC/DC双向变流器采用图1a拓扑结构，DC/AC变流器采用图2b进行分析。

3.1 DC/DC双向变流器控制

当电力电子调相机系统吸收有功或发出有功时，为了控制DC/AC变流器直流侧电压稳定，设计电压外环电流内环的控制方案。图3为DC/DC变流器控制策略，其中，eref，esm分别为DC/AC直流侧指令电压和反馈电压，iL为超级电容侧反馈电流。

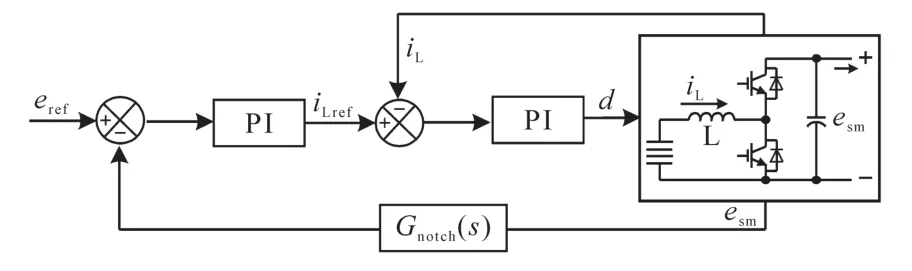
图3 DC/DC变流器控制策略Fig.3 Control strategy of DC/DC converter

3.2 DC/AC变流器控制

3.2.1 惯量响应控制

在传统的SVG控制策略中，有功功率环控制目标为直流侧的电压稳定，由于传统的SVG运行过程中存在损耗，需要吸收有功功率维持SVG系统的正常运行。类比于传统的链式SVG，H桥直流侧电压受双向DC/DC控制，给定的指令电压uref为超级电容器的电压，但是采取传统的控制策略无法控制链式SVG的惯量响应。因此，设计DC/AC双向变流器控制策略，如图4所示。

图4 有功功率环控制策略Fig.4 Control strategy of active power loop

图4中，uref为电压给定，vsk，isk分别为并网点PCC的三相电压和三相电流。

由于传统的控制策略无法响应系统的频率变化，在传统的无功功率环的基础上，改进有功功率环，构造网侧连接点PCC的频率和超级电容器电压指令的线性映射关系，则有：

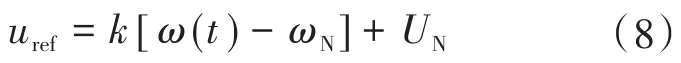
式中：k为映射系数；ω为电网实际角频率；ωN为额定角频率；UN为超级电容器额定电压。

假设超级电容器输出的有功功率为Pac，输出的功率和两侧的电压幅值的变化率相关，则有：

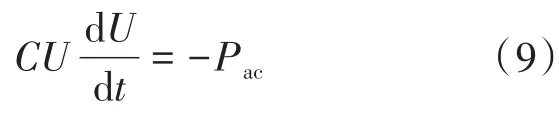
式中：U为超级电容器电压。

假设传统调相机输出的有功功率为Pe，由于调相机转子输入的功率为0，输出的功率仅仅和转动惯量和转速相关，则有：

式中：ωr为调相机转子转速。

因此超级电容的功率特性和传统调相机非常相似，如图5所示。

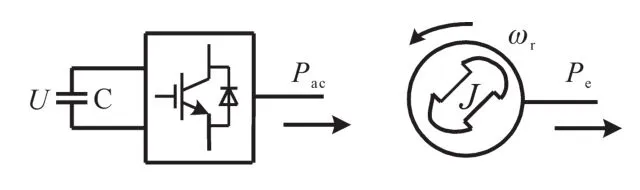
图5 超级电容类比调相机转子功率特性Fig.5 Comparison of rotor power characteristics between super capacitor and condenser

联立式（8）和式（9），可得随着网侧频率变化的网侧有功功率输出Pac为

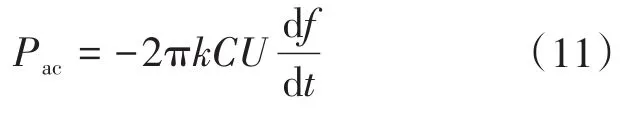
通过资料查证，国家电网公司对于惯量支撑也有一定的要求[12-13]，有功功率输出Pe为

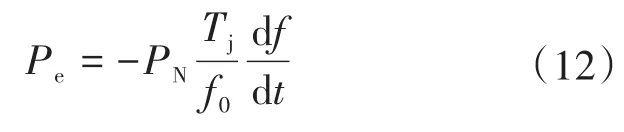
式中：f0为电网额定频率；f为电网实际频率。

通过对比推导的有功功率输出和国家电网公司对于惯量支撑的功率要求，具有一致性，理论上可通过对超级电容的电压控制间接进行惯量控制。

如式（8）所示，当网侧系统稳态运行时，ω保持额定频率不变，超级电容器的电压指令也保持在额定电压；当网侧系统出现扰动或者电能供需不平衡时，频率的波动通过式（8）线性映射到超级电容器电压。若记ω/ωN=ω*，U/UN=U*，则有：

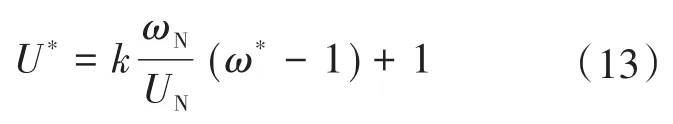
电压和频率存在线性映射关系，如图6所示。可以分析出，调整k的大小，可以改变频率和电压的映射关系，其中，k越大，映射到超级电容器的电压也就越大。

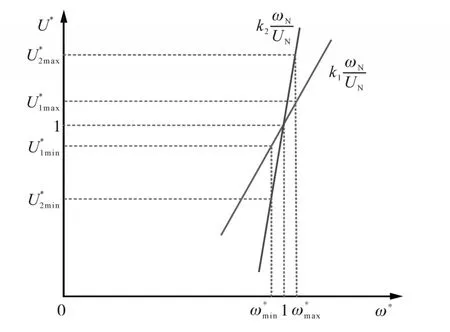
图6 电压和频率的映射函数Fig.6 Mapping function of voltage and frequency

3.2.2 无功功率控制

根据无功功率的需求范围，可以将无功控制分为系统级和装置级无功控制。其中，系统级无功控制是针对整个电力系统的无功需求，根据系统的无功指令，直接进行无功控制；装置级无功控制是针对网侧节点的无功需求，根据网侧电压的稳定，间接进行无功控制。

1）系统级无功控制。系统级无功控制目标为电力系统的无功功率指令，根据系统的需求进行调节。DC/AC变流器系统级无功控制策略如图7所示。

图7 系统级无功功率环控制策略Fig.7 Control strategy of system level reactive power loop

根据瞬时无功理论，得：

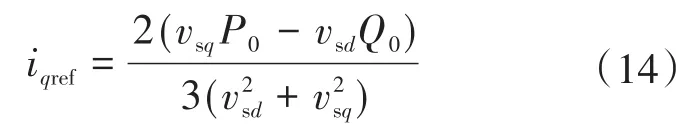
式中：P0为系统有功指令给定；Q0为系统无功指令给定。

由于稳态时仅仅做无功补偿，有功功率远小于无功功率，同时网侧电压q轴分量远小于d轴分量，因此式（14）可简化为

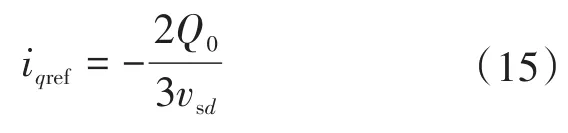
2）装置级无功控制。DC/AC变流器装置级无功功率环控制策略如图8所示。由于控制目标为网侧电压，通过一个电压外环即可实时跟踪网侧电压。

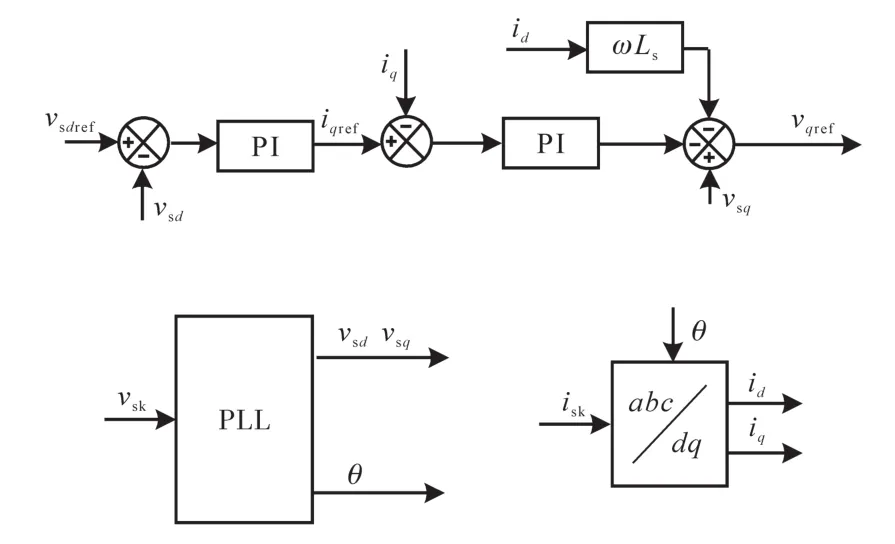
图8 装置级无功功率环控制策略Fig.8 Control strategy of device level reactive power loop

3.3 边界分析

电力电子调相机在网侧波动时，输出的功率受外界扰动和内部控制参数影响。由于超级电容器通过双向DC/DC变流器接入直流侧，而双向变流器的电压变比不能过大或过小，这限制了超级电容器的电压变化范围。

为了解决这个问题，在频率-电压的映射函数后，加入一个电压限幅，即将超级电容器的电压限制在一个范围内。当系统频率波动较大时，电力电子调相机为了自我保护，将电压限幅在恒定值，保证了电力电子调相机长时间稳定运行。

在装置级层面，限幅保证了DC/DC模块的效率和稳定性；在系统级层面，限幅保证了储能单元的配置不受系统功率扰动的影响。

4 调相机的对比分析

传统调相机和电力电子调相机的储能装置分别为转子和超级电容器。从能量利用率和惯量两个角度，具体分析电力电子调相机相比于传统调相机的优势。

4.1 能量利用率

由于能量越大，储能元件的体积以及损耗也就越大，因此，提高能量利用率，减小不必要能量的投入也是十分重要的。定义能量利用率：

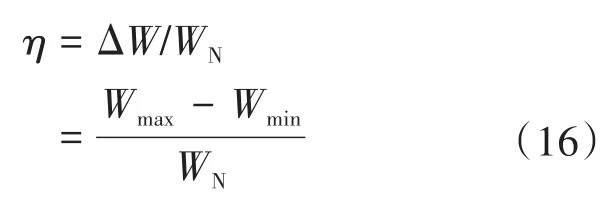
式中：Wmax为系统存储最大能量；Wmin为系统存储最小能量；WN为额定运行下系统存储能量。

记频率变化最大值和最小值分别为ωmax和ωmin，超级电容的电压最大值和最小值分别为Umax和Umin，有：

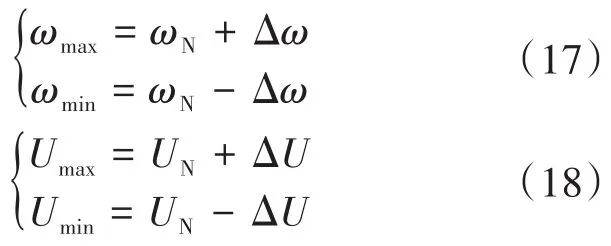
根据式（16）、式（17），则传统调相机能量利用率ηk为

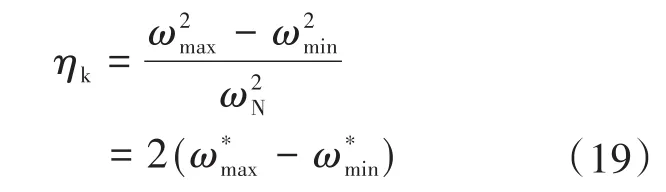
根据式（8）、式（16）、式（18），则电力电子调相机能量利用率ηc为

通过式（19）、式（20）可以分析出，当kωN/UN＞1时，电力电子调相机的能量利用率大于传统调相机，同时k越大，能量利用率也就越大。

4.2 惯量

对于传统的同步机，当转速发生变化时，其转子动能也发生变化，吸收或释放能量，对外表现为电磁功率的增减。记同步机电磁功率为Pek(t)，即

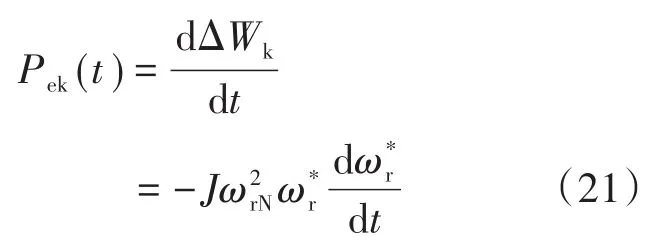
式中：ΔWk为同步机电磁能量的增减。

同理，记电力电子调相机电磁功率为Pec(t)，即

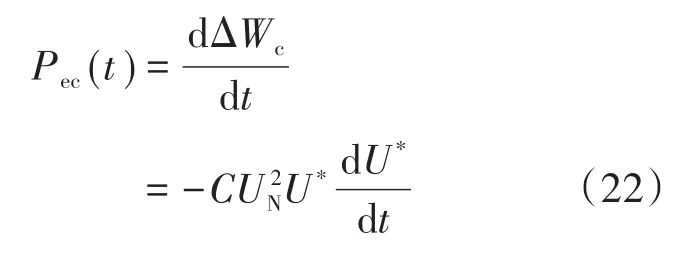
式中：ΔWc为超级电容能量的增减；U*为电压的标幺值。

为了达到传统调相机的惯量响应，当链式SVG的电磁功率等于同步机电磁功率时，即Pec(t)=Pec(t)，联立式（21）、式（22），得：

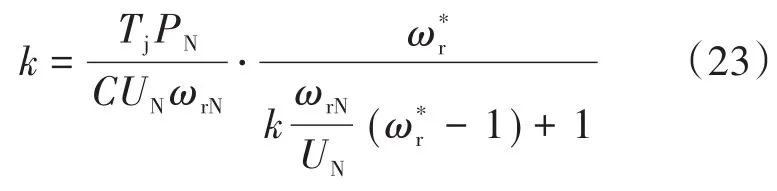
通过式（24）推导结果可以分析，针对制造好的同步机机械结构，时间惯量常数为Tj，可以通过设计电力电子调相机的动态参数k，实现类似的惯量响应功能；其次，相比于传统的同步机结构，由于链式SVG的映射参数k可以动态调整，将根据场景需求，更自由地应用于各种场景。

5 仿真研究

为验证本文理论分析的正确性，在PSCAD/EMTDC构建电力电子调相机、发电机、负载、扰动的系统仿真模型，其中电力电子调相机主电路拓扑采用链式拓扑，如图9所示。仿真环境配置参数如下：发电机容量166.6 kV·A，虚拟调相机容量83.3 kV·A，负荷83.3 kW，扰动41.6 kW，额定相电压481 V，电感2.67 mH，超级电容器电容0.416 F，额定电压600 V，直流侧电容4.2 V，电压800 V。

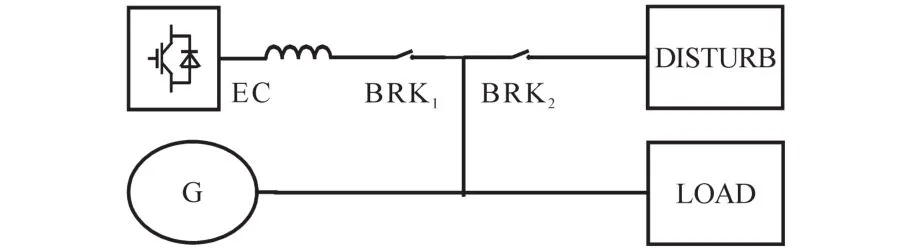
图9 电力电子调相机的仿真模型Fig.9 Simulation model of power electronic condenser

图9中，G为发电机模型，EC为电力电子调相机模型，LOAD为负载，DISTURB为扰动。BRK1在1 s时闭合，接入电力电子调相机；BRK2在3 s时闭合，接入负载扰动。

5.1 电力电子调相机功能验证

如图9所示，在1 s时接入电力电子调相机，可以迅速提供给定无功功率；在3 s时接入扰动负载，电力电子调相机可输出有功功率，减小频率波动。同时，无功功率在整个过程中几乎保持恒定值。

本节主要验证虚拟调相机的功能。如图10所示，在1～3 s时间内，虚拟调相机提供无功功率，同时吸收少量有功维持电容电压稳定；在3～4 s时间内，无功功率保持不变，同时由于负载的扰动，有功功率随着系统频率变化而变化，且在4 s后到达最大值；随着频率的回升，4 s后输出的有功功率逐渐降低，且在8 s后逐渐趋向稳定。

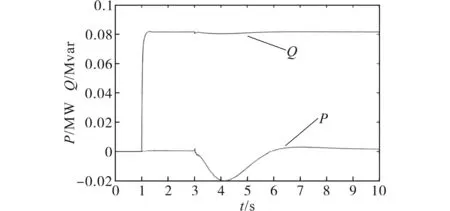
图10 k=0.005 9时的有功功率和无功功率Fig.10 The active power and reactive power when k=0.005 9

如图11所示，超级电容器电压和网侧频率是具有相同趋势的波动波形，当k=0.005 9时，频率在5 s时达到最低点0.96，通过式（10）可以计算出电压最低点为0.83，与仿真的波形一致。

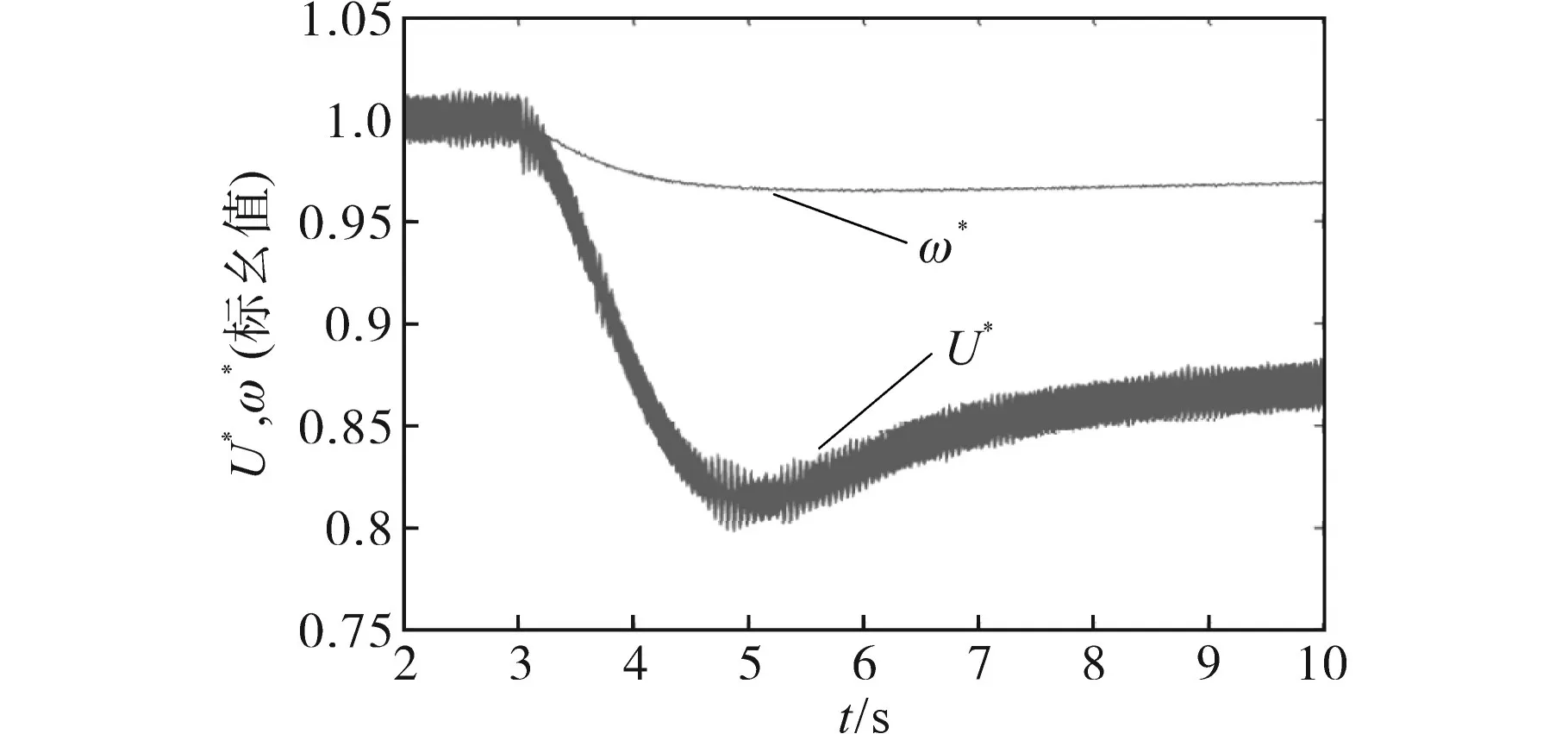
图11 k=0.005 9时的超级电容器电压和网侧频率对比图Fig.11 Comparison diagram of super capacitor voltage and grid side frequency when k=0.005 9

5.2 边界条件

为了验证电压限幅的效果，增大动态参数k=0.017 7，同时将电压限幅在额定值的±0.3（标幺值），采用图9所示仿真模型进行仿真。

本节主要验证了超级电容器电压保护策略，由于k越大，虚拟惯性时间常数也就越大，所需要的能量也就越大，而超级电容本身提供的能量有限。为了解决该冲突，电压幅值限幅，可以间接控制能量输出。k=0.017 7时的有功功率和无功功率如图12所示，在整个过程中，无功功率仅仅在3 s有略微波动；有功功率在3 s开始跟随频率变化而变化，且在6 s后随幅值控制策略而降为0，超级电容电压也已经稳定，虚拟调相机将仅仅提供无功功率。

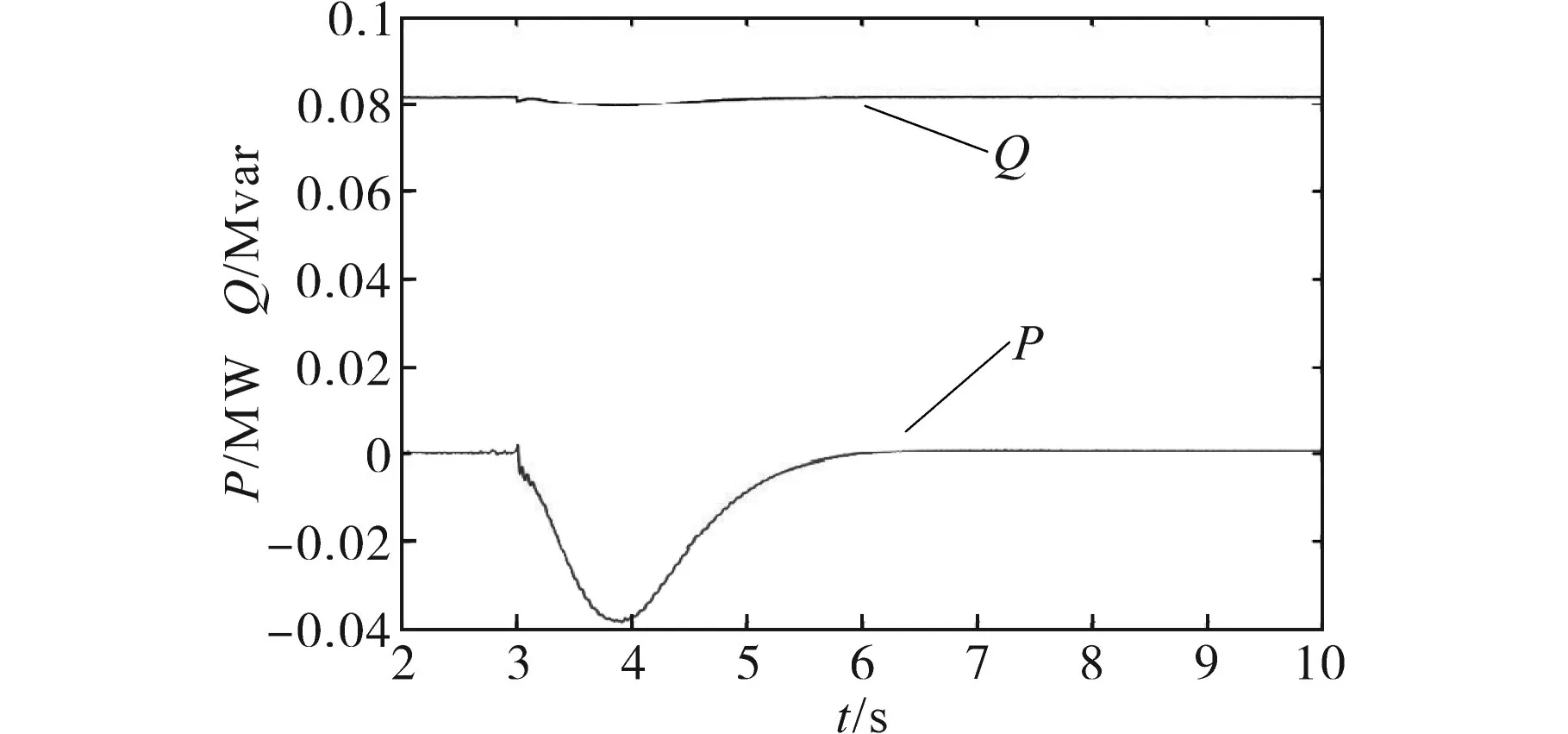
图12 k=0.017 7时的有功功率和无功功率Fig.12 The active power and reactive power when k=0.017 7

如图13所示，由于增大动态参数k=0.017 7，根据频率-电压的映射关系，给定电压将会超过最小的电压幅值，电压将会被限制在0.7（标幺值）。即6 s之后，即使频率存在波动，电力电子调相机为了自我保护，已经停止放出有功功率，并且吸收一定的有功功率维持电压的恒定。

图13 k=0.017 7时的超级电容器电压和网侧频率对比Fig.13 Comparison diagram of super capacitor voltage and grid side frequency when k=0.017 7

5.3 对比分析

为了对比电力电子调相机和传统调相机的功能，将图9中的电力电子调相机替换成传统调相机模型，如图14所示。

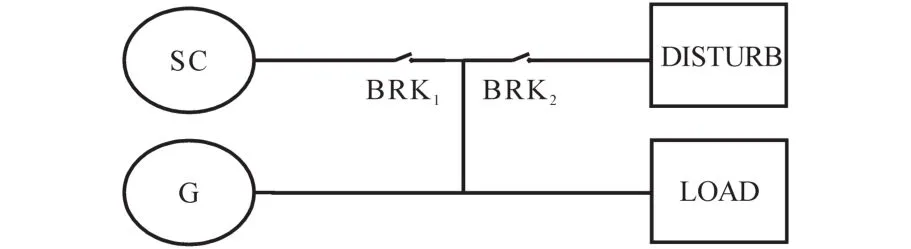
图14 传统调相机的仿真模型Fig.14 Simulation model of traditional condenser

采用频率电压的控制策略，见图9。选择k为0，0.002 9，0.005 9，0.011 8分别进行仿真，同时，将电力电子调相机换成传统调相机，根据式（24）设置k对应的Tj并分别进行仿真，共得到8条频率响应曲线。其中，k为0，0.002 9，0.005 9，0.011 8分别对应Tj为0，1.99，3.98，7.96。本节主要验证了电力电子调相机和传统调相机的对比关系，频率响应对比图如图15所示，当k为0，0.002 9，0.005 9时，3 s后，频率响应在下降的过程中，两者可以较好拟合，在5 s之后频率逐渐回升，两者略微有差异。当k=0.011 8时，3 s后，频率响应在下降和回升的过程中，两者均有略微差异。可以分析出，当k比较小时，电力电子调相机可以较好拟合传统调相机的惯量响应，k越大，拟合度越差，但是仍可以反映调相机变化的趋势。

图15 传统调相机和电力电子调相机的频率响应Fig.15 Frequency response of traditional and power electronic condenser

6 结论

针对传统SVG的低惯量问题，提出了具有动态无功补偿和动态惯量响应能力的电力电子虚拟调相机。通过对电力电子虚拟调相机的拓扑结构、储能环节、控制策略的设计以及和传统调相机的对比分析，得到的具体结论如下：

1）该电力电子虚拟调相机，可以提供系统级或装置级的无功需求，同时可以虚拟惯量响应阻尼电网频率波动。

2）针对不同容量大小、电压等级的电网环境，设计合适的拓扑结构；针对需求的额定容量和惯量相应时间，配置相应大小的超级电容容量，以减小成本，提高效益，同时，设计超级电容单元串并联参数，为虚拟调相机具体投入提供参考。

3）电力电子虚拟调相机的概念设计对于高比例新能源电力系统的稳定运行具有现实意义。