基于混合GA算法求解车间调度问题
王 粟,陈新彦,曾 亮
(湖北工业大学 电气与电子工程学院,湖北 武汉 430068)
0 引 言
在如今数字化车间普及的时代,工作车间调度问题(job shop scheduling problem)更为优化的解决,对先进制造技术的进一步发展十分关键[1]。
使用优化算法来解决车间调度问题,难免会出现收敛速度与局部最优之间的矛盾,为了尽可能减小带来的影响,已经有很多不同改进的优化算法被应用在解决JSP上[4]。魏胜利等[5]使用了改进的生物地理学优化算法处理车间调度问题;叶彦斐等[6]在基于传统遗传算法的基础上,将种群灾变机制加入到算法的遗传环节中以预防种群早熟收敛,寻优能力明显提高;曹坤煜等[7]以最小化最大完工时间为目标建立了生产调度模型,并在此模型的基础上设计了一种收敛速度和求解稳定性均较优的免疫遗传算法。尽管上述方法取得了一定的效果,但是探索新的方法求解JSP仍在不断进行。
本文针对JSP提出了一种混合GA算法,主要从变异策略和种群生成两方面进行了改进。一方面,对遗传算法中的变异算子的改进,根据种群的平均适应度值来决定是否进行变异操作,使变异朝着确定的方向进行,加快了收敛速度;另一方面,当变异趋势的确定后,将会造成种群的多样性下降、收敛速度过快的问题,这些问题就使得出现局部最优解的可能性上升,于是本文借鉴SA算法的重升温策略,使用PSO算法中的个体极值来代替GA算法的特定代数的种群,帮助在寻优迭代过程中跳出局部最优,增强了全局搜索能力。借鉴SA算法的改进思想,使得PSO算法更好优化GA算法,最终使该算法能更加快速、高效找出JSP的最优解。
1 车间数学模型
1.1 符号定义
本章节使用的所有数学符号及其代表的含义见表1。

表1 数学符号
1.2 模型建立
优化目标选择车间调度问题中最常使用的最小化最大完工时间[8],有如下表达式
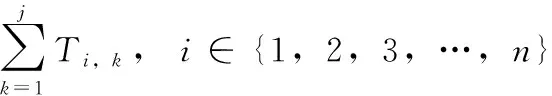
(1)
目标函数
f=min{Cmax}
(2)
约束条件:
(1)由于工件本身加工上的工艺约束,对每个工件来说,必须在前一道工序加工完成后才能加工后一道工序
Si,j>Si,j-1
(3)
(2)对于任意一台机器,如果正在对某个工件的某道工序加工,其它工件不得在此时间段使用该机器,保证一台机器只能加工一个工件
∀Mk⊂M,x、y∈{1,2,3,…,m},x≠y, ∃Mx,η,θ,My,α,β
(4)
2 GA算法和PSO算法简介
对遗传算法来说,其特有的遗传操作,使得种群的多样性丰富,增强了全局搜索的能力,减少了陷入局部最优解的风险[9]。但较强的全局搜索能力意味着需要较大的迭代次数,才能在寻优迭代的过程找到最优解。这就说明了遗传算法相对于其它优化算法来说,收敛速度较慢,要较长的时间才可以使种群进化到包含近似最优解的状态,最终在全局最优解位置收敛[10]。
而对粒子群算法,其核心要素就是用来更新粒子在解空间位置的速度-位移公式,具体如下
vij(t+1)=w·vij(t)+c1r1[pij(t)-xij(t)]+c2r2[pgj(t)-xij(t)]
(5)
xij(t+1)=xij(t)+vij(t+1)
(6)
其中,c1、c2为加速因子,c1体现了粒子对自身历史位置记忆能力的强弱,反映了粒子向历史个体极值趋近的快慢;c2体现了粒子对整个种群最优位置信息汲取能力的大小,反映了粒子向历史全局极值趋近的快慢[11]。可以看出c1代表着粒子对自身“认知”能力的好坏,而c2代表着粒子间有效信息共享能力的优劣。r1、r2代表[0,1]范围内的均匀随机数。pij(t) 代表第i个粒子迄今为止搜索到的最优位置,pgj(t) 代表整个粒子群迄今为止搜索到的最优位置。对于具有保证粒子运动惯性的控制参数w,反映了粒子对前一代速度的保持能力的大小[12]。vij(t)、vij(t+1) 分别代表粒子当前的速度和迭代一次后的速度,而xij(t)、xij(t+1) 分别代表粒子当前的位置和迭代一次后的位置。从公式中可以很明显的看出,这些关键的控制因子并没有随搜索过程的变化而变化。对于不同的迭代次数,即不同的“外界环境”,也就需要不同大小的控制因子,才能更好发挥控制因子的效果,从而使得算法能够准确高效地寻找出问题的最优解。
3 混合GA算法
本文中提出的混合GA算法,结合了GA算法和PSO算法,根据第2节分析这两种经典优化算法的优劣。首先详细阐述了混合GA算法的思想,说明了如何借鉴SA算法中的重升温策略,使PSO算法更好补偿GA算法的缺陷,接着针对它们在处理车间调度问题的不足之处,改进了GA算法中的变异策略,并在PSO算法中引入了自适应控制因子和排列操作,然后描述混合GA算法的步骤总流程并画出该算法的流程图,最后通过仿真验证了混合GA算法思想的可行性。
3.1 混合GA算法的思想
改进变异策略的遗传算法依据平均适应度值来判断是否进行变异操作,提高了收敛速度,有效解决变异的随机性的问题。但对于某些特殊的初始种群,改进变异策略的遗传算法大概率会得出局部最优解。分析改进变异策略的遗传算法未产生更优解的原因有两点:一是可能由于收敛速度过快;二是在整个进化过程中,个体包含最优解的特征少,很难产生最优解。对于收敛过快的情况,借鉴模拟退火算法中的重升温策略,由于收敛过快造成陷入局部极小值停滞不前时,可以通过将粒子群算法产生的个体最优位置代替遗传算法中迭代特定次数种群的位置,从而跳出局部最优解,调整搜索进程。之所以采用个体最优位置,因为个体最优解包含全局最优解的大多数特征,这正好弥补了最优解特征少的缺陷,在寻优迭代过程中,通过粒子间的协同合作与知识共享,对最优解的寻找起到一定的辅助作用。
3.2 变异策略
遗传算法的变异操作虽然保证了种群的多样性,但变异并没有一个确定的方向,随机性较强。在改进的变异操作中,舍弃了传统意义上决定变异比列的变异概率,在一定程度上违背了自然规律,但这样对于具体的问题,能够尽早收敛,提高效率[13]。伪代码如下:
Input:
第r条染色体的适应度值为Sr;第g代经过选择和交叉操作种群的平均适应度值为avgfitnessg;
Procedure:
IfSr>avgfitnessgthen
将该染色体执行变异操作;
End
Output: 经过变异操作的染色体;
判断是否变异不再由随机数与变异概率的大小关系来决定,而是根据种群的平均适应度值来决定。对进行了选择和交叉操作的种群求其适应度的平均值,然后对大于该平均值的进行变异操作,小于该平均值的不进行变异操作。
3.3 种群生成策略
本文使用PSO算法产生的个体极值种群代替GA算法特定代数的种群,为了使PSO算法在处理车间调度这一具体问题能发挥良好效果,引入了改进的自适应控制因子和排列操作。
3.3.1 自适应学习因子和惯性权重因子
粒子群算法的控制因子在整个迭代过程中,始终保持不变。但随着迭代次数的增加,种群所处的解空间的环境在不断发生着变化,所以为了使控制因子更好控制寻优过程向着好的方向进行[14],本文对学习因子和惯性权重因子进行了改进,公式如下
(7)
(8)
其中,c1max、c2max为c1、c2的最大值,c1min、c2min为c1、c2的最小值,i表示当前迭代次数,maxgen1表示最大迭代次数。可以从上式看出,在算法开始时,赋给c1、c2较小值,接近cmin, 使粒子对自身先前速度的记忆能力较弱,在一定程度上保证粒子在偏离原先的寻优轨迹上进行搜索,进而在未知的解空间中展开寻优探测,体现了全局搜索;而在算法执行后期,迭代次数i接近maxgen1,c1、c2有较大值,接近cmax, 则粒子对上一次迭代时具有的速度维持能力较强,使得粒子在近似原先的搜索范围进行更为深入的探索,根据原有的寻优轨迹在附近范围来搜索更好的解,体现了局部搜索。
另外,对惯性权重因子w也进行了动态调整,表达式如下
(9)
其中,wmax、wmin代表惯性权重因子的最大值和惯性权重因子的最小值, max(pbest)、 min(pbest) 分别代表个体极值的最大值和最小值,pbest(j) 代表当前粒子的个体极值,k为当前迭代次数[15]。上式反映出,对于个体极值较小的粒子,赋给的惯性权重因子较大,维持粒子历史速度的能力较强,便于粒子在原有的搜索轨迹上进行更细致的搜索;对于个体极值较大的粒子,赋给的惯性权重因子较小,维持粒子历史速度的能力较弱,便于粒子在偏离原有的搜索轨迹上进行“开发”。而最后的部分e-k是随着迭代次数的增加而减小,使得在算法开始时,具有较强的“探索”能力,而在算法的后期,具有较强的“开发”能力。
3.3.2 排列操作
对于车间调度这种采用实数编码的问题,引入了一种新的进化操作——排列操作。排列操作的方法是:随机截取染色体的一部分,包含x个基因位,对这x个基因位随机排列,共有x!种情况,再随机从中选取一种来替代之前的染色体片段。与变异操作和交叉操作所起到的作用相似,排列操作的作用也是增加种群的多样性,但不同的是排列操作能够产生更加多种的情况,特别是采用实数编码的染色体,操作简单且效果明显。排列操作如图1所示,从图中可以看出随机选择了5个连续的基因位,所以共有5!=120种可能的替换情况,此图中是将5-2-2-6-7替换为2-5-6-7-2。图1(a)是父代选择出的部分基因位,图1(b)是进行排列操作后的子代部分基因位。
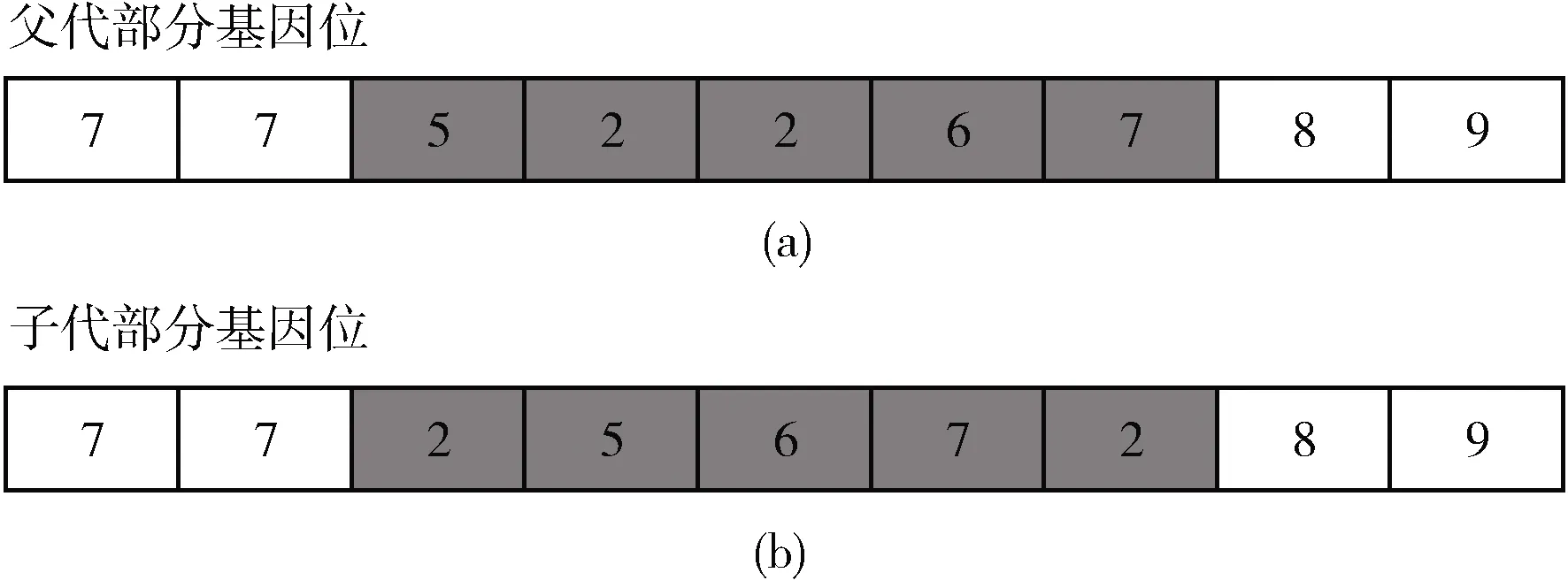
图1 排列操作方法
3.4 混合GA算法基本流程
综上所述,混合GA算法步骤具体描述如下:
步骤1 初始化参数,产生初始种群。
步骤2 计算种群的适应度值。
步骤3 判断迭代次数是否等于最大迭代次数n。
步骤4 如果条件不满足,则依次进行选择、交叉、变异、保优操作,并计算当代种群中个体的适应度值,保留每代中的最优个体,转到步骤3。如果条件满足,再判断改进后的遗传算法是否产生了更优解,如果产生了更优解,则输出该解;否则,使用粒子群算法迭代k次,得到由个体极值组成的种群。
步骤5 将由个体极值组成的种群代替遗传算法的第k代的种群。
步骤6 转到步骤2,重复上述步骤直到算法达到终止条件,输出最优解。
混合GA算法流程如图2所示。
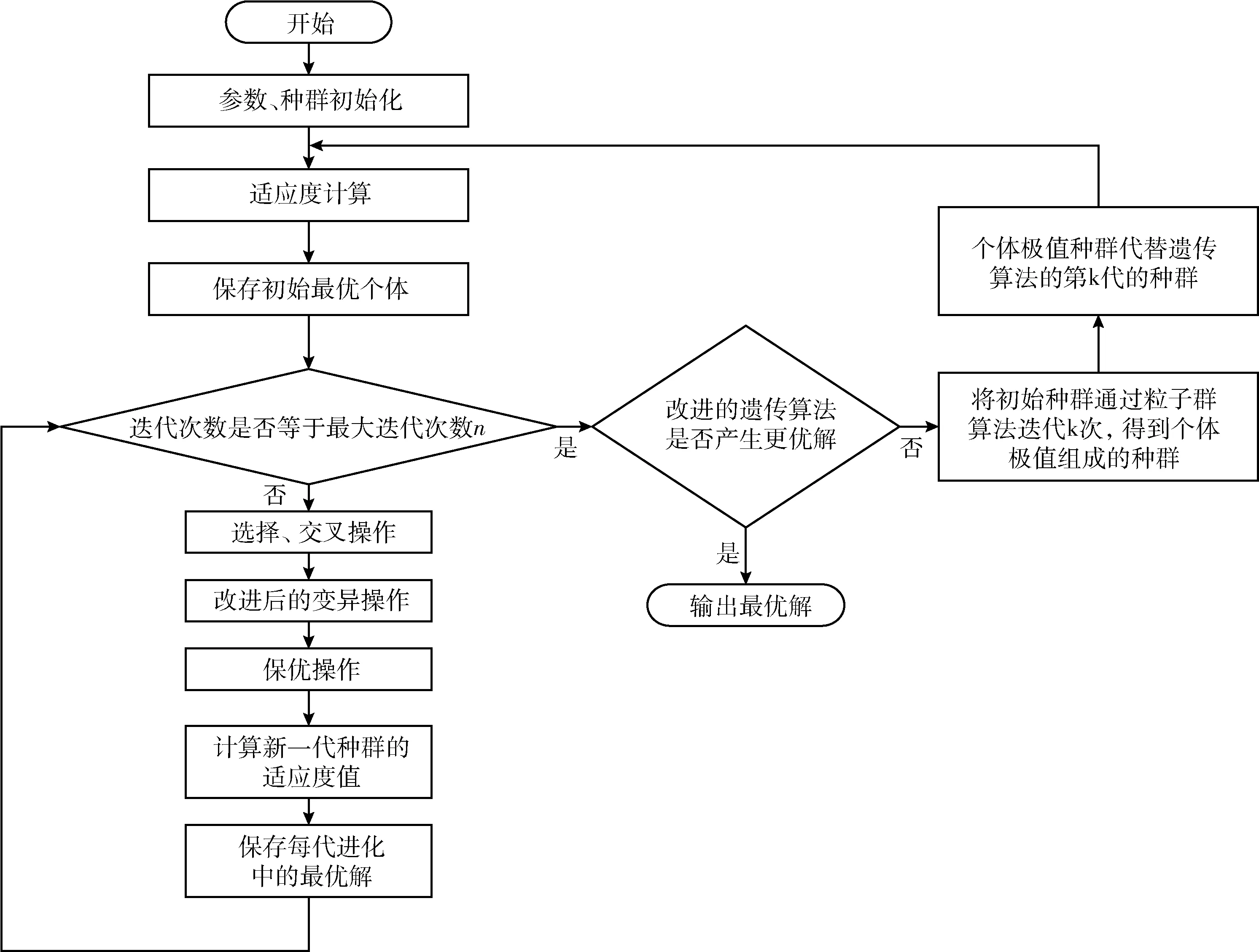
图2 混合GA算法流程
3.5 混合GA算法思想测试
如果仅仅改进变异策略的GA算法对寻找更优解有效果时,直接输出最优解。而当改进变异策略的遗传算法未得出更优解时,使用了粒子群算法产生的个体极值代替遗传算法迭代特定次数的种群,不仅弥补了改进变异策略可能带来收敛速度过快的问题,也有效应对了初始种群随机产生所带来的影响。分别以粒子群算法产生的个体极值作为第50代种群和以遗传算法原始的第50代种群完成迭代的进化曲线如图3所示。
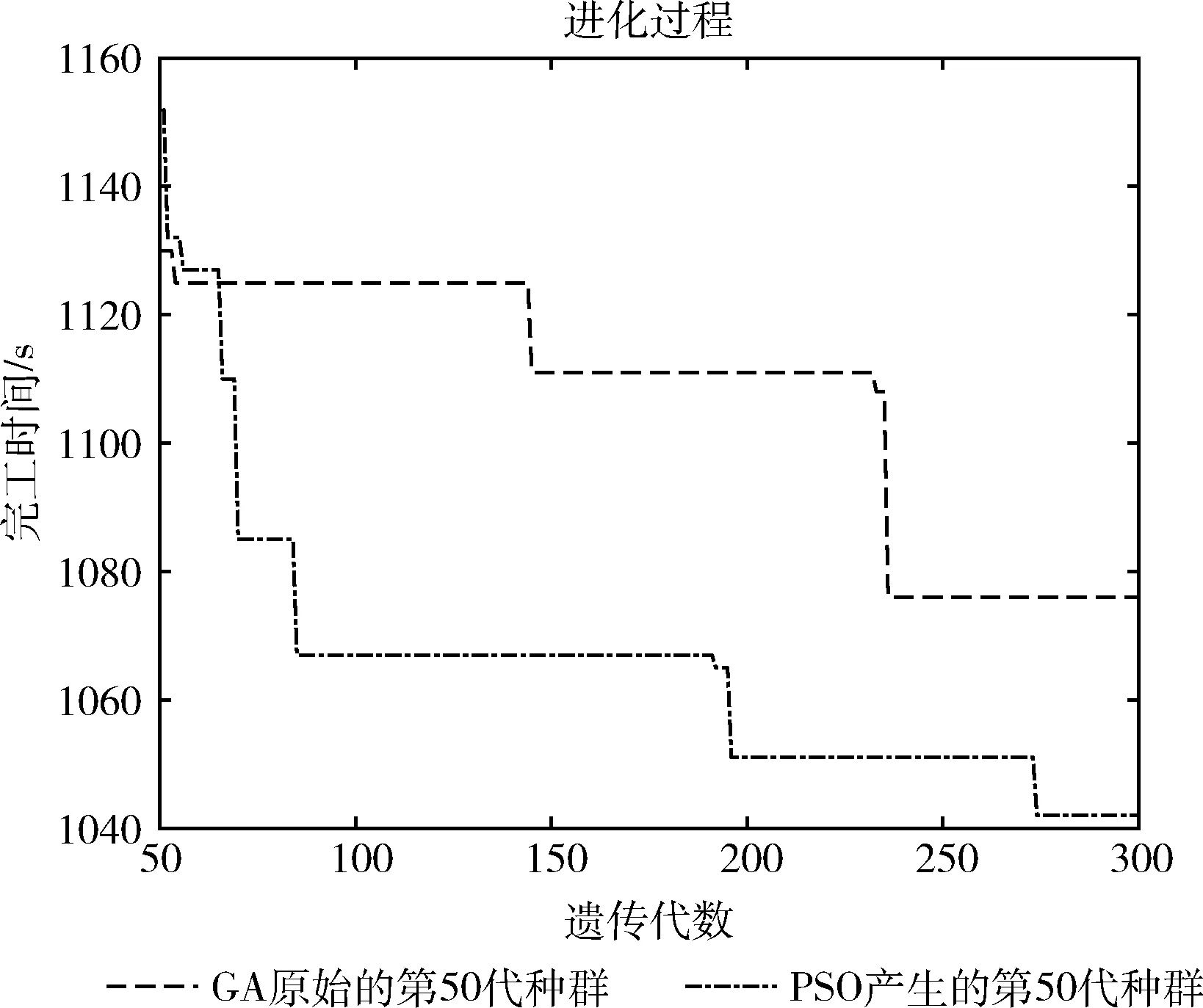
图3 效果对比
图3是在第4章提到的测试算例MNO_10中得出的,其中图中虚线是先通过粒子群算法对初始种群进行迭代50次,将产生的个体极值组成的种群代替遗传算法的第50代的种群,再使用遗传算法进行迭代250次得出的进化曲线;而点画线是对同一初始种群直接使用遗传算法完成迭代,截取50~300代的进化曲线。从对比图可以很明显看出,使用粒子群算法迭代50次产生的个体极值组成的种群与遗传算法第50代的种群,前者的目标函数值高于后者的目标函数值,符合自己的分析,起到了重升温的效果。同时,由于通过粒子群算法产生的种群由个体极值组成,其中携带最优解的特征元素较多,最后产生的最优解也要更加优良。
4 车间调度仿真
4.1 测试算例生成
本文为验证混合GA算法(hybrid optimization genetic algorithm,HOGA)求解所提问题的性能,使用车间调度问题中3种不同规模的算例进行测试。其中,每个测试算例的机器数量、工件数量和工件的加工工序数都不相同,分别为10台机器、10个加工工件、每个工件有10道工序;8台机器、8个加工工件、每个工件有8道工序;6台机器、6个加工工件、每个工件有6道工序。以10台机器、10个加工工件、每个工件有10道工序的这个测试算例为例,命名为MNO_10,则另外两种测试算例分别命名为MNO_8和MNO_6。此外,每台机器有各自的工艺约束,只能够加工某些工件的某些工序。对于工件的某道工序,只能在固定的机器上进行加工。测试算例MNO_10的调度加工时间与加工机器见表2,测试算例MNO_8的调度加工时间与加工机器见表3,测试算例MNO_6的调度加工时间与加工机器见4。

表2 MNO_10调度加工时间与加工机器
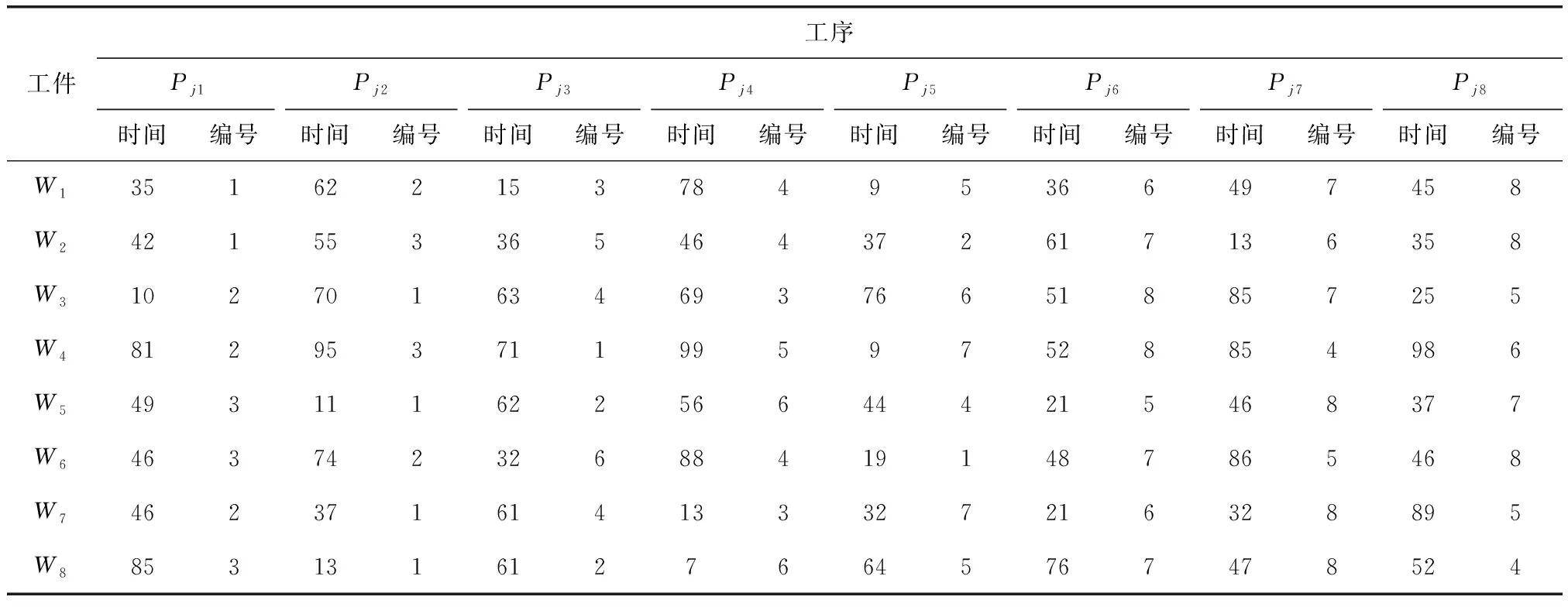
表3 MNO_8调度加工时间与加工机器
4.2 参数配置
对HOGA的初始种群规模设置为20、最大迭代次数为300、使用粒子群算法产生个体极值种群的迭代次数为50、交叉率为0.8、保优率为0.05;对GA的初始种群规模、最大迭代次数、交叉率、保优率不变,此外的变异率为0.01;对PSO的初始种群规模、最大迭代次数不变,此外的学习因子为1.5,惯性权重因子为0.8,粒子的最大速度为35,粒子的最小速度为0。
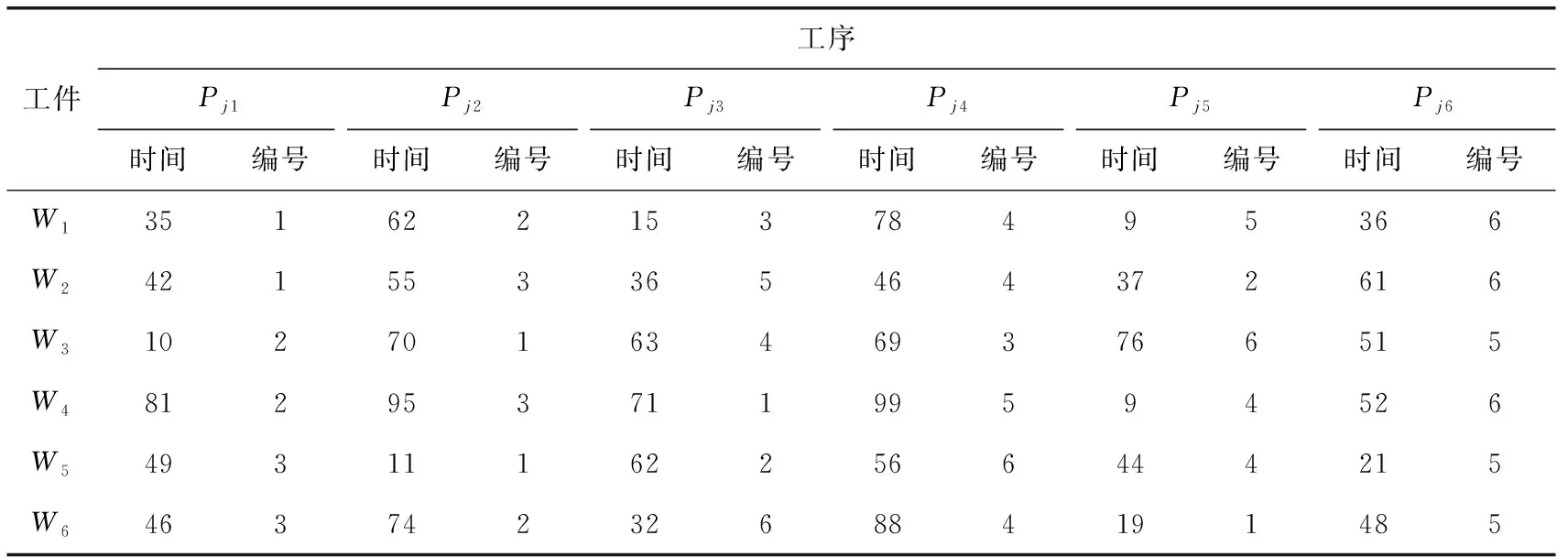
表4 MNO_6调度加工时间与加工机器
4.3 算法对比分析
HOGA、GA、PSO这3种算法在测试算例MNO_10上对应甘特图分别如图4(a)、图4(b)、图4(c)所示,在测试算例MNO_8上对应甘特图分别如图5(a)、图5(b)、图5(c)所示,在测试算例MNO_6上对应甘特图分别如图6(a)、图6(b)、图6(c)所示[16]。
从图4、图5、图6对比可以发现,通过HOGA对工序优化排序后,相较于GA和PSO这两种算法来说,充分利用了有限的加工机器,提高了效率,缩短了总加工时长,体现HOGA在解决车间调度问题上的优势。3种算法的分别在MNO_10、MNO_8、MNO_6这3种测试算例中的进化曲线如图7、图8、图9所示。
对比HOGA、GA、PSO这3种算法在3种不同的测试算例中的进化曲线图,可以清楚看出,首先在同一个测试算例中,对于同样的初始种群,HOGA不仅在搜索的初期具有较快的收敛速度,而且在后续搜索中具有较好的跳出局部最优的能力;而对于PSO和GA来说,容易陷入局部最优解,导致最终所输出的最优解并不是实际的最优解。

图4 MNO_10对应的甘特图

图5 MNO_8对应的甘特图
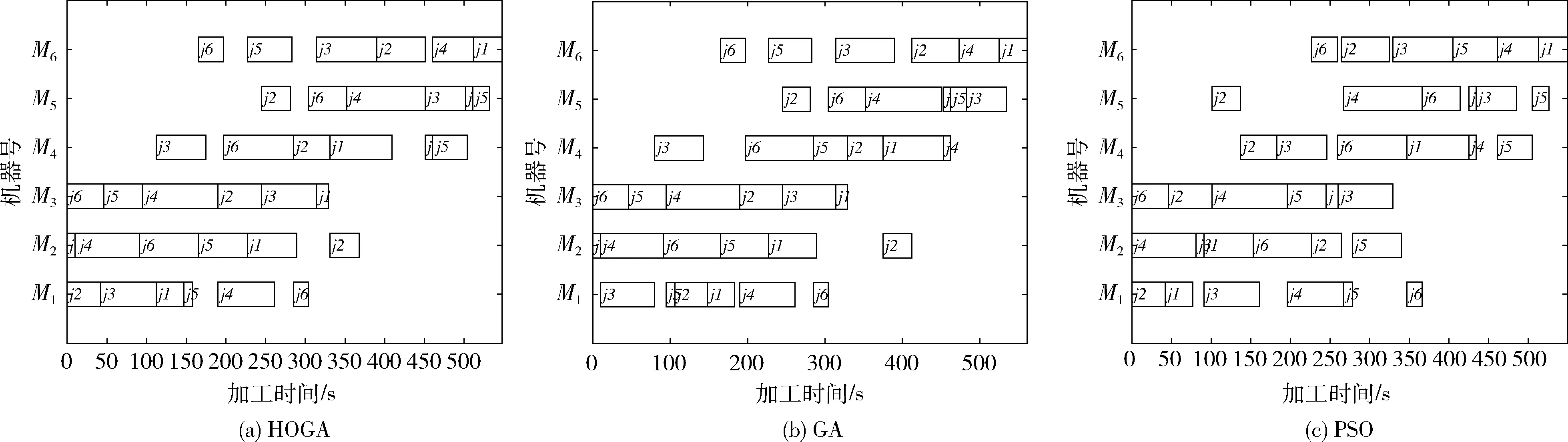
图6 MNO_6对应的甘特图
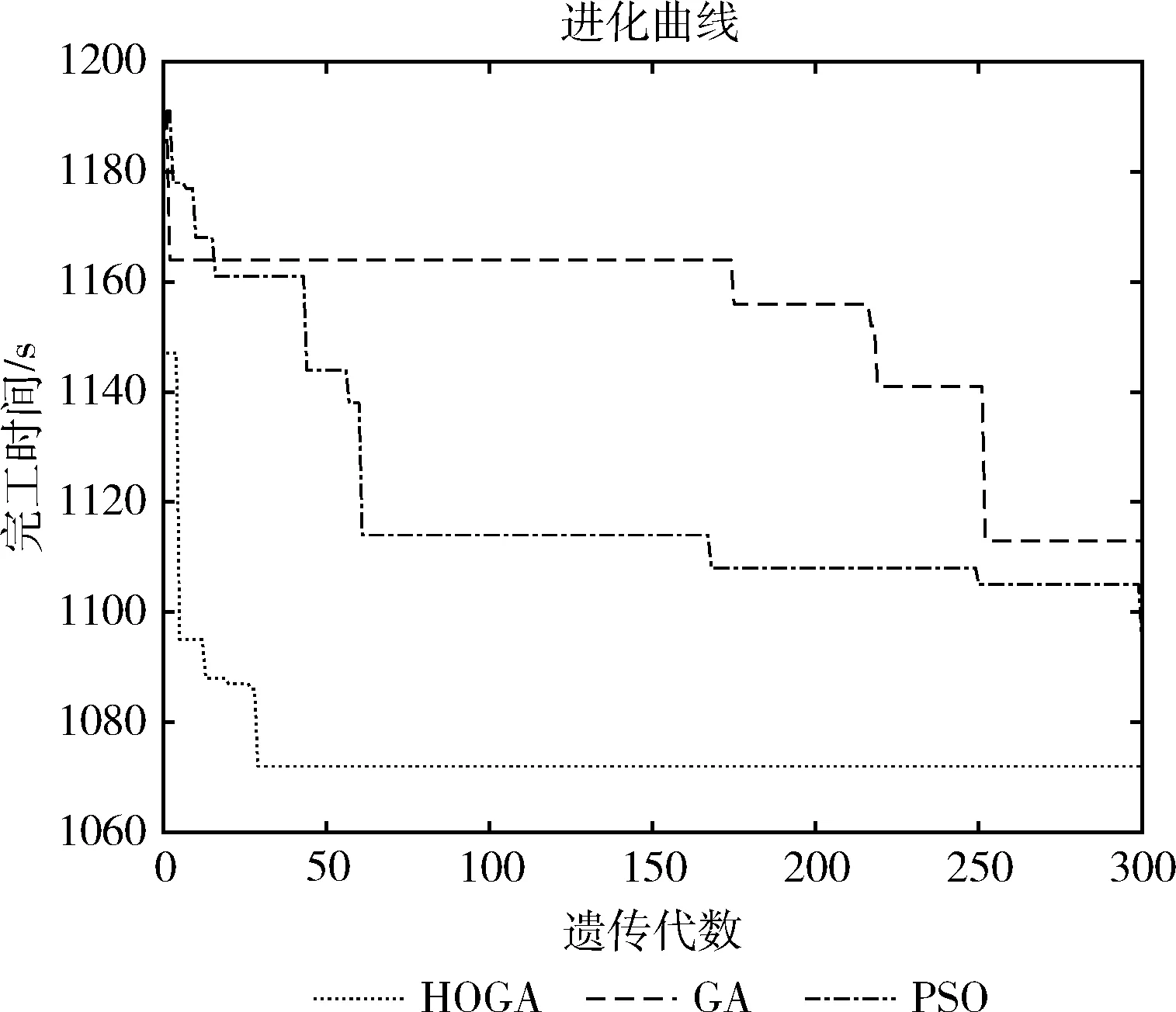
图7 MNO_10的算法收敛性对比
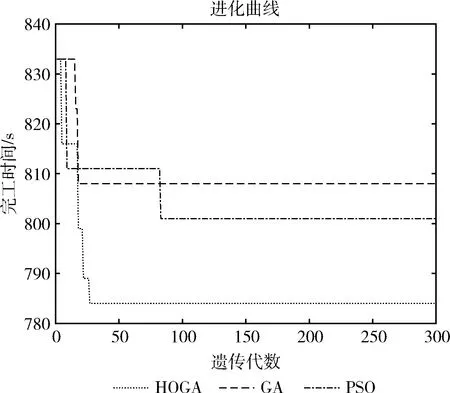
图8 MNO_8的算法收敛性对比
而在HOGA处理规模较大的MNO_10测试算例时,对比另外两种算法,取得最优解之间的差异更大;而在处理规模较小的MNO_6测试算例时,HOGA凭借它优异的性能仍然能够最大限度找出更好的最优解。HOGA达到了预期的优化效果,优于PSO和GA。测试结果的汇总见表5。

图9 MNO_6的算法收敛性对比
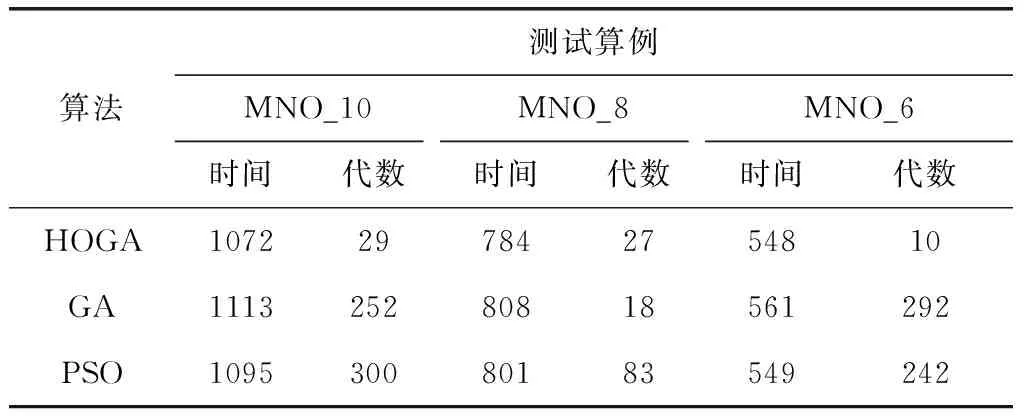
表5 测试结果汇总
5 结束语
本文结合车间调度问题,提出了一种混合GA算法:该算法首先改进了GA算法的变异操作策略,减小了传统变异的随机性带来的影响,加快了收敛速度;然后借鉴模拟退火算法思想,将PSO算法产生的个体极值种群代替GA算法迭代特定次数的种群,有效解决了初始种群随机产生造成的问题,并跳出了局部最优解,起到重升温的作用,最终达到快速、高效得出全局最优解的目的。通过MNO_10、MNO_8、MNO_6这3个测试算例进行实验仿真比较,验证了混合GA算法的优势。下一步,将从PSO算法中参数寻优方面开展工作,进一步优化混合GA算法的性能。

