基于SDN架构的垂直切换算法

唐 鑫，徐彦彦，潘少明，宋方振

(武汉大学 测绘遥感信息工程国家重点实验室，湖北 武汉 430000)

0 引 言

垂直切换是指移动用户在异构无线网络中实现网络切换的技术[1]。考虑多属性网络参数的垂直切换算法能获得较好的切换性能[2-7]。但目前大部分研究均采用分布式计算，切换结果容易集中指向少部分优质网络，无法实现全局网络资源的均衡利用。软件定义网络(software defined network，SDN)架构可实现网络设备的集中管理与控制[8]，并能快速适应节点的位置变化，是开展面向全局网络的多属性垂直切换算法设计的关键[9]。但节点的移动性可能改变节点所处网络环境，导致依据当前状态进行的决策不再适用。事实上，可以利用马尔可夫(Markov)模型开展网络状态转移及预测[10,11]，选择未来时刻性能最优网络。研究结果表明，用户网络访问行为具有长时间的周期性和短时间内的突发性，其接入网络带来的网络状态变化也与时间序列密切相关，考虑多个时刻的状态将获得最佳的网络状态属性预测[12]。

本文提出一种基于SDN架构的垂直切换算法，首先利用SDN数据平面收集全局网络状态和节点的参数信息，然后在控制平面通过所设计的模糊逻辑控制模型对网络多属性参数进行离散化和归一化处理。在此基础上，设计一种二阶Markov模型[13]，综合考虑不同时刻的影响对未来全局网络的实际状态进行预测，并基于全局网络回报评估开展垂直切换决策，最终实现在不同的节点移动条件下都能有效降低局部不可靠的切换决策，保证切换后的网络性能。

1 基于SDN的算法框架

算法利用SDN集中控制、数据平面与逻辑平面分离的架构，在数据平面采集全局网络属性参数，控制平面通过模糊逻辑控制模型对全局网络属性参数进行归一化决策处理、权重分布和网络收益计算，再通过二阶Markov预测模型对切换后的实际网络回报进行预测，最终评估全局网络回报后下发流表以完成切换决策，具体算法框架如图1所示。其中，控制平面中的模糊控制和二阶Markov过程为基于SDN框架引入的多属性决策支撑算法，而SDN架构为多属性决策支撑算法提供输入信息收集和决策实施支撑。

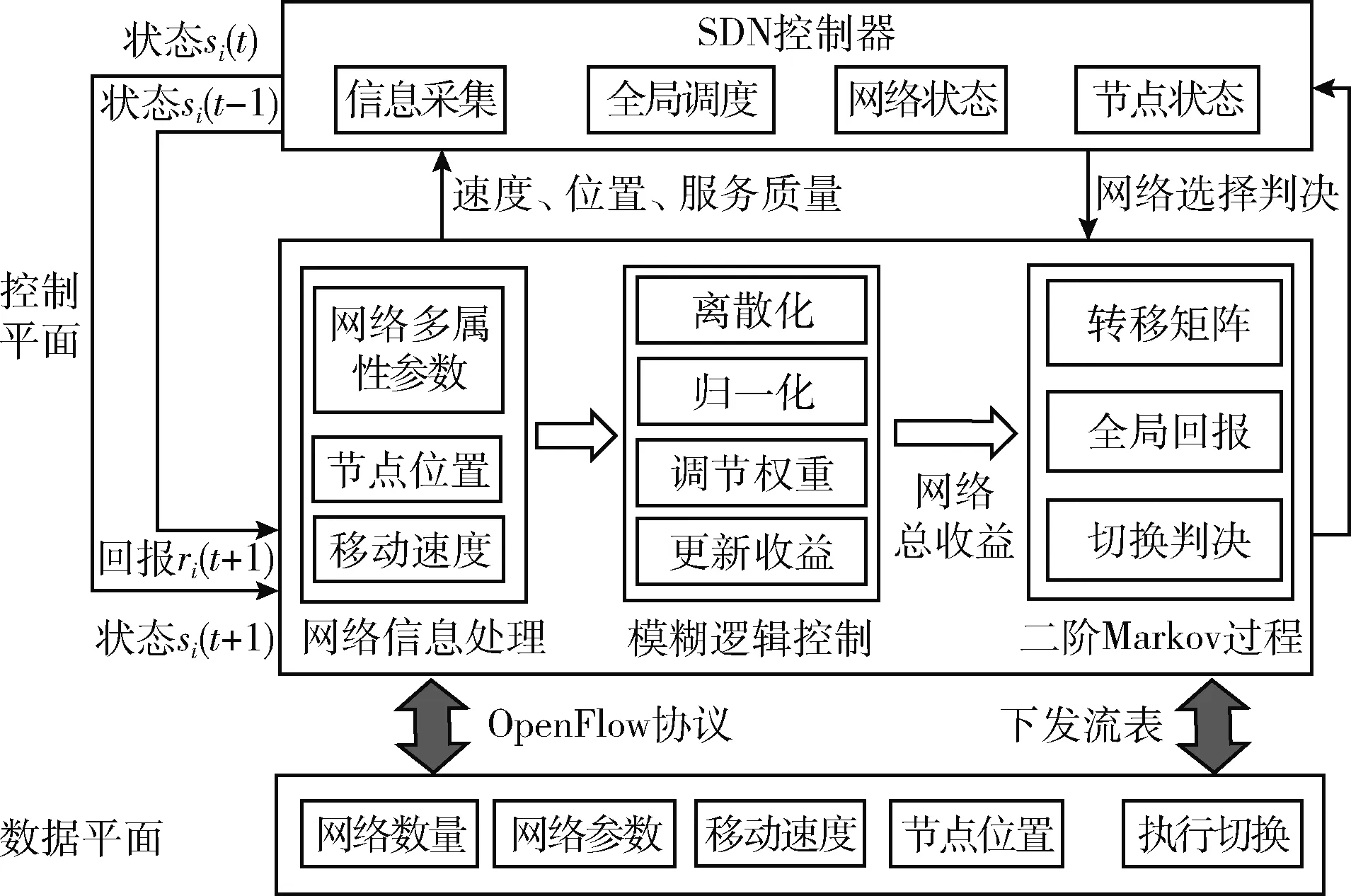
图1 基于SDN的垂直切换算法框架与决策模型

如图1所示，由SDN数据平面采集可达网络与移动节点的多属性信息(包括网络数量、网络参数、节点位置和移动速度)，SDN控制器将收集到的多属性信息传递到模糊推理系统，进行离散化、归一化、权重调节和收益更新得到网络收益参数。根据所获得的历史网络收益参数，利用二阶Markov转移状态矩阵和回报函数，预测切换后的网络状态并据此进行全局网络回报评估，以选择全局范围内网络整体收益最大的目标网络。最终控制平面将决策结果以流表的形式下发至移动节点，移动节点根据指令完成网络切换处理。

2 模型与算法设计

2.1 网络模型及多属性参数收集

研究表明，考虑多属性参数的垂直切换算法能实现较好的网络切换性能[2-7]，因此收集全局网络的多属性参数是实现最优垂直切换的前提。为此，SDN的数据平面，以周期T来采集节点位置信息(X,Y)、节点移动速度v和网络参数信息。控制平面估算无线信号强度RSS、 网络传输时延De、 网络实际传输带宽Bw、 丢包率Dr和多普勒频移fd等网络参数。

引入相应网络的RSS计算模型获得信号强度参数估计，RSS(dBm)计算模型为

RSS=Rj-RLij

(1)

其中，Rj表示无线接入点j的传播功率(dBm)，RLij为无线接入点j到移动终端i的传输信号衰减(dB)，其可以通过式(2)进行计算

RLij=PL+10α×log(dij)+Z

(2)

其中，PL表示无线接入点的固定功率损耗(dB)，α∈[2,4] 表示路径损耗系数，dij表示移动终端i和无线接入点j之间的距离(km)，Z是均值为0的正态分布随机变量，表示信号的衰落(dB)。

网络实际传输带宽Bw可采用瓶颈带宽和往返传输时延(bottleneck bandwidth and round-trip propagation time，BBR)算法[14]进行估算，而丢包率Dr可以简单的通过一段时间之内的输入输出报文数量进行计算[14]

(3)

时延De计算

De=报文到达时间-报文发送时间

(4)

多普勒频移fd越大，无线信号瑞利衰减的速度越快，影响无线通信的质量[15]，其计算式为

(5)

其中，λ为无线电波长，θ为无线电波入射方向与用户移动方向的夹角，v为节点移动速度。

2.2 模糊逻辑控制模型及收益评估

显然，由于异构网络中各参数属性值具有不同的意义，无法在一个尺度和平面上对所有属性参数进行统一评估，如某些参数越大，表明切换后所获得的实际网络状态性能越好；而反之另一些参数越大则表明切换后所获得的实际网络状态性能越差。同时，由于不同网络属性参数的尺度不同、变化幅度各异，直接进行简单对比难以突出不同属性参数的差异化特点，因此所设计的模糊逻辑控制模型需要对所有属性参数根据其不同特性进行归一化处理，并在归一化处理的基础上形成统一尺度的评估输出。

不失去一般性，设网络模型收集获得的多属性参数个数为N，当前节点位置为(X,Y)，对应的异构网络中包含有M个候选网络和Z种不同的网络模式。则在考虑网络参数属性对网络状态性能贡献的基础上，对任意网络m的任意属性n可设计如下的参数归一化收益计算方法

(6)

式中：Qm,n表示第m个网络的第n个属性值，qm,n表示Qm,n的离散化取值，参数rn∈[1,-1] 为不同类型属性的收益调节因子，对于值越大表示网络状态越好的属性参数，如带宽、网络信噪比等，其对应的收益为正收益，设置其rn=1； 相反对于值越大表示网络状态越差的属性参数，如丢包率、网络开销等，其对应的收益为负收益，设置其rn=-1， 其中m∈[1,…,M]，n∈[1,…,N]。

考虑到不同网络参数对不同网络影响程度不同，针对M个网络的Z种网络模式以及其N个网络参数，构建网络决策因子矩阵

(7)

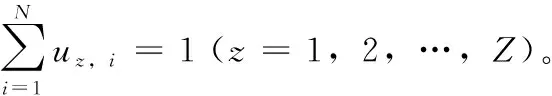
wm,n=uz,n·km,n

(8)

其中，m=1,…,M;n=1,…,N;z=1,…,Z。 即可得到时刻t，针对某网络m多属性总收益Tbenefit(m) 有

(9)

2.3 基于二阶Markov的网络预测算法

按照异构无线网络垂直切换的要求，为实现全局最优的网络性能，需要在切换后获得最佳的网络回报，因此根据切换后的实际网络状态评估网络的总收益而非切换前的网络状态评估网络总收益才是获得最佳切换决策的关键。

为此，不失去一般性设网络状态可以离散化表示为有限的 {s1,s2,…,si,…,sl} 状态集，其状态空间为S， 其中si∈S(0≤i≤l) 表示网络所处的一种状态，其由该网络m的所有属性参数进行描述，即

si={Qm,1,…,Qm,n}

(10)

若在当前时刻t的网络状态为s(t)∈S(0≤t≤l)， 则预测的目的是获得下一时刻t+1的网络状态，以根据t+1时刻的网络状态计算切换后的网络总收益，并根据所获得评估收益进行切换决策。

由于网络是一个随时间变化的序列事件，因此，t+1时刻的网络状态可以根据历史时刻的网络状态进行估计，即网络的Markov状态转移满足如下关系

P(s(t+1)|s(1),…,s(t))

(11)

综合考虑网络变化的长时间周期性和短时间内突发性的特征，使用二阶Markov模型，则网络的下一时刻的状态仅与当前时刻和上一时刻网络状态相关，上式可简化为

P(sk(t+1)|si(t),sj(t-1))

(12)

即t+1时刻的状态仅仅与t时刻和t-1时刻的状态相关。则对某网络m，若设t-1时刻状态为sj(t-1) 且t时刻状态为si(t) 时，下一时刻t+1状态为sk(t+1) 的概率为pi,j,k(m)， 可以得到网络m其不同状态下的状态转移概率矩阵为

(13)

显然，根据Markov基本原理有

(14)

式(14)表明，从t-1刻的状态sj(t-1) 和t时刻的状态si(t) 转移到t+1时刻所有状态的总概率为1。

2.4 回报评估与切换决策

基于式(9)给出的某网络m的总网络收益估计以及式(13)给出的切换后网络状态属性概率，可以得到切换到该网络后的整体回报为

(15)

其中，δj,i为当前状态指示符，当s(t-1)=sj(t-1) 且s(t)=si(t) 时δj,i=1否则δj,i=0。

基于式(15)，可以得到切换到不同网络的不同回报，即R(sj(t-1),si(t))={r1(sj(t-1),si(t)),…,rM(sj(t-1),si(t))}， 则可以得到切换决策为

(16)

即选择使网络全局回报函数最大化的网络m′， 作为状态处于si(t) 和sj(t-1) 时的切换目标网络。其中rm(sj(t-1),si(t)) 表示网络m的整体回报函数取值，M为全局环境下的候选网络数目。

具体的切换算法见算法1。

算法1：控制平面切换判决算法

输入：移动节点信息，网络参数信息

输出：切换判决结果

(1)遍历网络，初始化模糊逻辑参数U、k、Qm,n， 确定网络的二阶Markov状态转移概率矩阵P(m)

(2)whilet

ift≥2T

1) 数据平面采集节点信息(X,Y),v和网络参数

2) 控制平面：

for m from 1 toM

估算参数RSS,De,Bw,Dr,fd

模糊逻辑计算网络m的总收益Tbenefit(m)

二阶Markov预测全局回报rm(sj(t-T),si(t))

end for

切换决策←全局回报最大的网络m′

控制平面下发决策流表

end if

t←t+T

end while

3 性能分析

3.1 网络参数设置

仿真实验搭建在Ubuntu20.04.1操作系统上，利用Mininet-Wifi网络仿真器，采用OpenFlow1.3协议版本，与基于SDN框架的Ryu控制器相结合，实现异构网络的垂直切换仿真。由于Mininet-Wifi仿真器的限制，仿真场景设置为4种采用工作802.11协议标准的无线接入网络实现异构组网，具体参数见表1。尽管这些网络协议标准因为工作频段和编码类型等原因，存在部分网络互相兼容的情况，但由于网络传输带宽和信号覆盖范围不同，可认为组成异构网络。网络环境配置了24个WLAN网络(4种802.11标准的网络各配置6个)，每个网络信号的覆盖范围是40 m～130 m。移动节点的移动速度变化范围为[1,11] m/s，移动节点的数量变化范围为[200,600]。实验中，设置2.2节中所提网络参数[3]标度k=5，决策因子排序[3]为RSS>fd>Bw>Dr>De。

表1 仿真网络参数

实验结果统计平均切换次数、切换失败数量、网络回报、平均切换时延和丢包率作为评判依据：

(1)平均切换次数。切换次数越高，网络越不稳定，处理时延越高。切换将产生数据从原有的缓存列表发送到新的缓存通道的时延，随着切换次数的提高，数据传输和处理时延将造成大量的数据排队，在拥塞网络中将导致缓存区溢出形成丢包。

(2)切换失败次数。失败次数越高，切换判决性能越差。当终端根据垂直切换判决结果对相应基站发起接入请求时，而当前网络的接入节点数量已饱和，则终端的切换请求将被拒绝。

(3)网络回报。异构网络中不同网络的参数不可直接比较，通过模糊逻辑输出网络收益值，利用上文提到的网络回报计算式(15)，评估网络的整体性能。

(4)平均切换时延和丢包率。垂直切换过程中，平均切换时延越低，用户感知越低，越接近无缝切换的需求。平均丢包率越低，切换选择的网络质量越高。

3.2 仿真结果分析

将所提出的算法与基于模糊控制的多属性决策切换策略的TOPSIS算法[16]、基于改进Markov算法[10]来对比，验证所提出的SDN控制器利用数据平面收集得到的数据，通过二阶Markov过程预测未来网络回报值的效果。

图2展示了3种算法多次实验后算法产生的平均切换次数对比结果，其中，节点数固定为200，节点移动速率为10 m/s，实验20次。从图2中可以得出，本文提出的算法平均切换次数比单纯使用模糊控制的TOPSIS算法和Markov算法更少，表明考虑多个时刻网络状态预测的有效性和SDN控制器位置管理和网络管理的全局性和实时性，能够提高算法的稳定性和合理性。

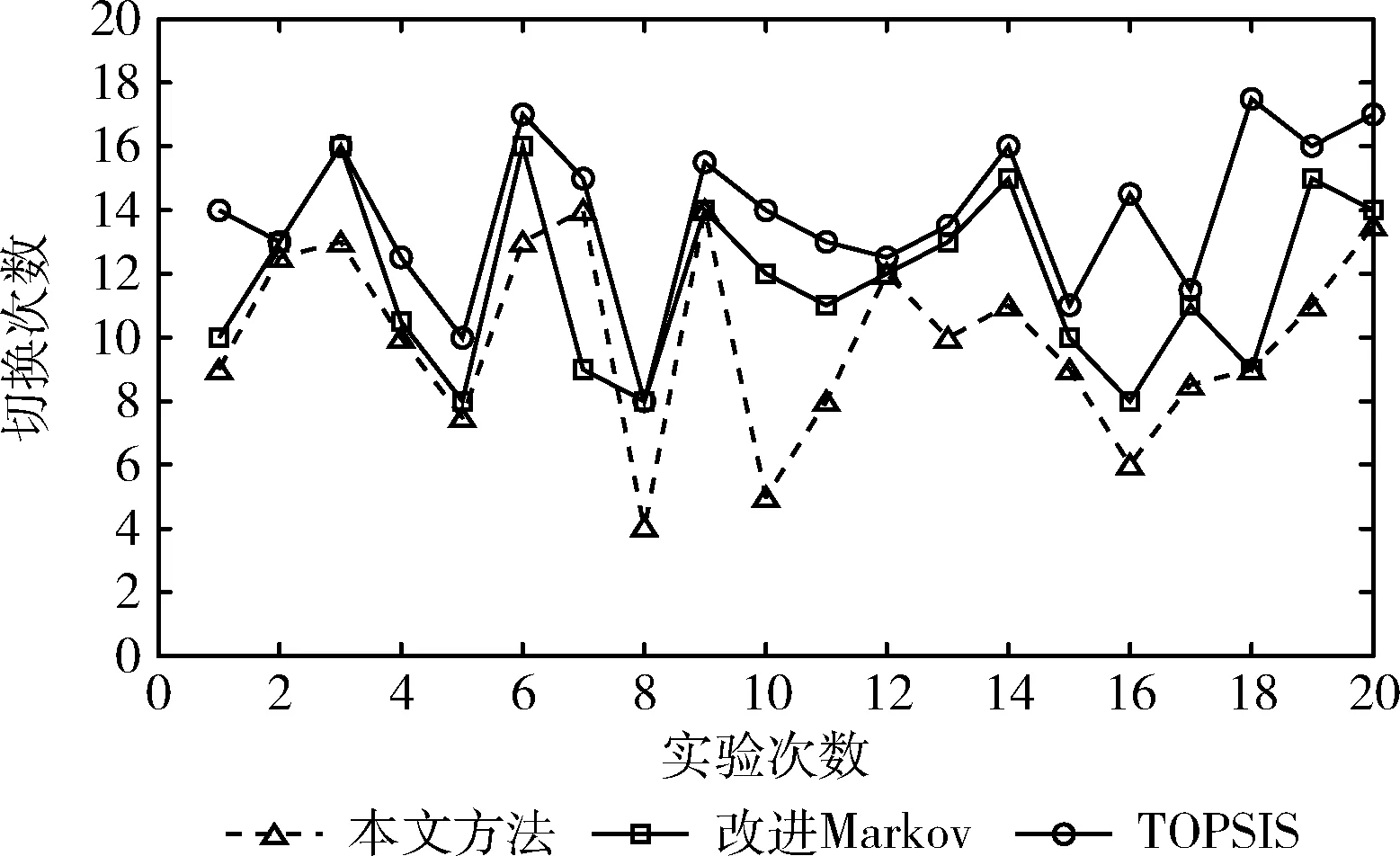
图2 平均切换次数实验对比

如图3所示，随着移动节点数目增加，本文算法切换失败次数明显低于TOPSIS，说明算法中央控制有效，避免了移动节点集中切换到优质网络。此外，算法失败次数略小于Markov方法，切换决策实现了一定程度的长期收益最大化，以及SDN架构能够提高网络信息管理，进一步提高网络资源分配。

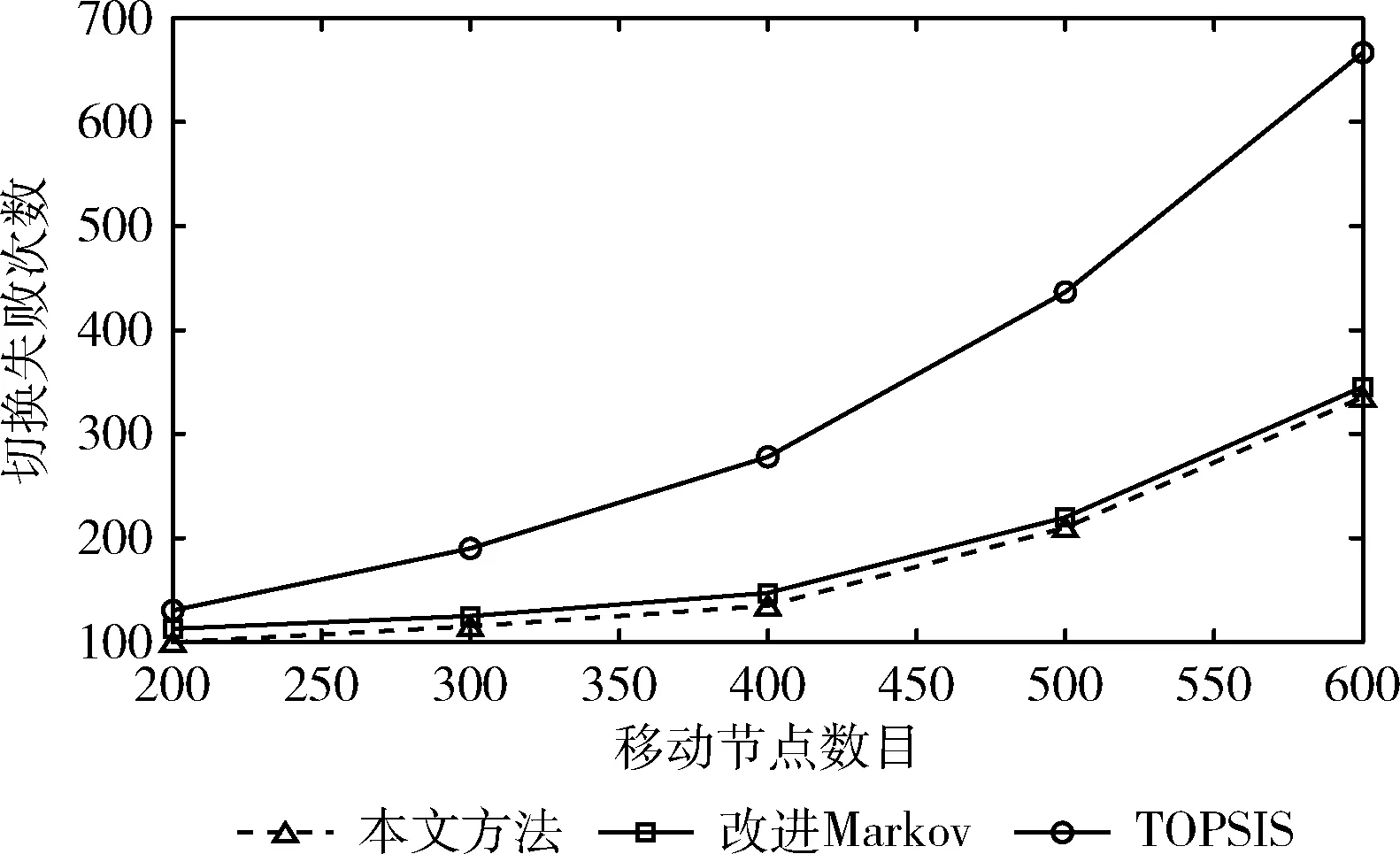
图3 切换失败次数实验对比

图4展示了随着节点移动速度的增加，本文算法的网络整体回报值依旧保持相对稳定，而TOPSIS算法和改进Markov算法的回报值不断降低。这是因为所提出的算法综合考虑节点上一时刻和当前时刻的状态，对切换判决过程中可能产生的中断进行预判。同时，TOPSIS算法和改进Markov算法每个节点需要额外的网络信息采集和处理开销，才会随着节点速度增加性能降低。

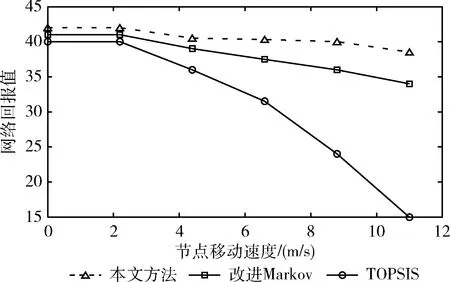
图4 移动速度增加时网络总回报值实验对比

图5和图6展示了在不同算法下的平均切换时延和平均丢包率的比较结果。本文算法优于传统的TOPSIS和改进Markov算法，说明结合SDN的算法能够快速有效下发流表，降低节点处理数据和交互信令的时延，有效提高平缓效率。同时，得益于SDN高效统一管理网络的优点，与采用分布式管理的改进Markov算法相比，数据传输的平均丢包率大大降低。

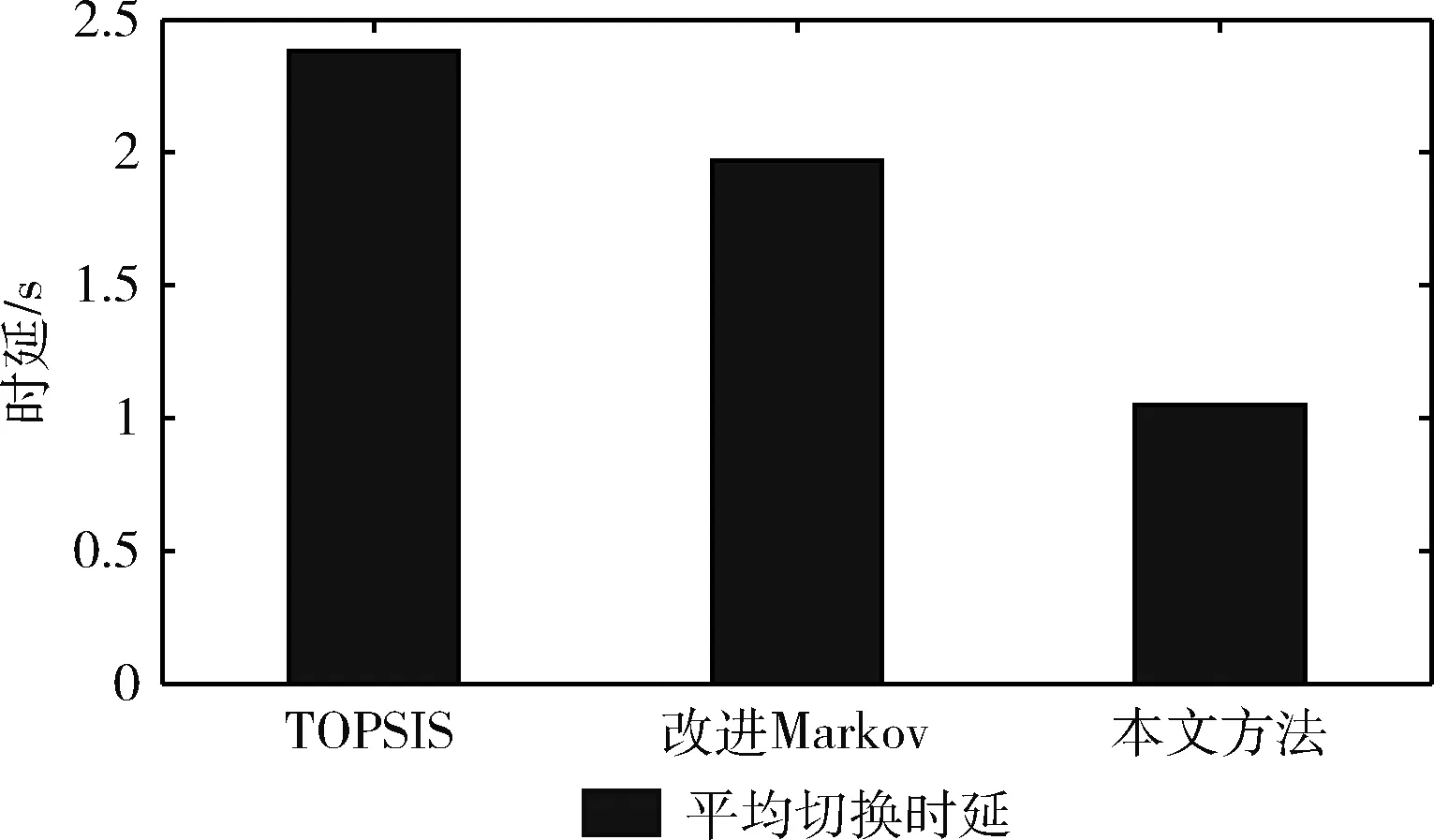
图5 平均切换时延实验对比

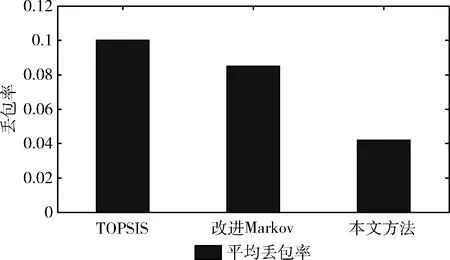
图6 平均丢包率实验对比

本文所提出来的基于SDN的垂直切换算法，虽然提高了切换性能，但相较传统的分布式算法而言，增加了许多交换机和控制器之间交互的信令开销，因此算法的性能瓶颈将依赖于控制器的处理能力。初始建立时的注册信令、节点移动时的匹配信令、流表维护的下发信令等都是无法避免的，具体开销的统计结果如图7所示。

图7 节点移动产生的信令开销

本文算法与经典TOPSIS相比，节点平均切换次数明显降低，切换失败次数明显更少，网络回报值也能保持稳定，切换性能优势明显；与单一时刻预测的改进Markov分布式算法相比，平均切换时延和丢包率降低，集中控制思想提高了用户使用网络的稳定性，保证切换后的网络质量。同时，集中控制的思想会带来的信令开销，对控制器的处理能力有要求。

4 结束语

针对目前大部分垂直切换算法中采用分布式局部寻优的“自私”策略，集中接入热门网络可能造成的网络拥塞考虑现象，提出一种基于SDN架构的垂直切换算法，结合二阶Markov模型和模糊逻辑进行垂直切换决策。算法通过SDN控制器将收集到的移动节点和网络信息参数，利用模糊逻辑控制器动态更新多属性参数的权值，二阶Markov决策器根据模糊逻辑输出结果预测网络全局回报并切换判决。实验结果表明，该算法在异构网络多属性切换判决中，能够有效减少局部、不可靠、无效和短收益的网络切换决策，降低切换时延和丢包率，为用户提供稳定的网络服务。