对胡克定律实验中密绕紧贴弹簧的问题及修正研究

王立斌

（复旦大学附属中学，上海 200433）

1 研究背景

“探究弹簧弹力与形变量的关系”的实验，以下简称“胡克定律”实验，是探究弹簧在发形变时，其形变与弹的定量关系，得到“弹簧发弹性形变时，弹的大跟弹簧伸长（或缩短）的长度成正比”的规律，即胡克定律.本实验隶属于高中物理课程标准（2017版）“必修1中1.2相互作用与运动定律主题”，属于学生必做实验.［1］

在教学实践过程中，导致实验结果与实验预期结果不一致的原因很多，弹簧自身的问题是一个重要的因素.笔者在对“胡克定律”实验装置和实验过程进行优化的基础上，对因密绕紧贴弹簧而产生的问题进行了研究，提出了修正弹簧的方法，并对修正方法进行了实验检验.

2 问题的产生

原实验装置如图1所示，主要用到弹簧、刻度尺、钩码、铁架台、铁夹等.实验时通过在弹簧下端添加钩码改变弹簧伸长，记录钩码质量和对应的弹簧长度.悬挂钩码时的弹簧长度减去未挂钩码时弹簧的长度，即为弹簧伸长.每次钩码平衡时，钩码的重力等于此时弹簧的弹力.

图1 原实验装置

通过画弹簧弹力与弹簧伸长的关系图（F-x图），即可探究弹力与形变量的关系.有时会出现如图2所示的F-x图.在弹力与形变量的关系图中，截距不为0，则不能说明弹簧弹力与形变量成正比.产生这种图像的弹簧如图3所示，外观具有密绕圆圈紧贴的特点.通过交流，笔者了解到，这种案例并非个案，具有一定的普遍性.但并未见到相关解释资料.笔者对此进行了研究.

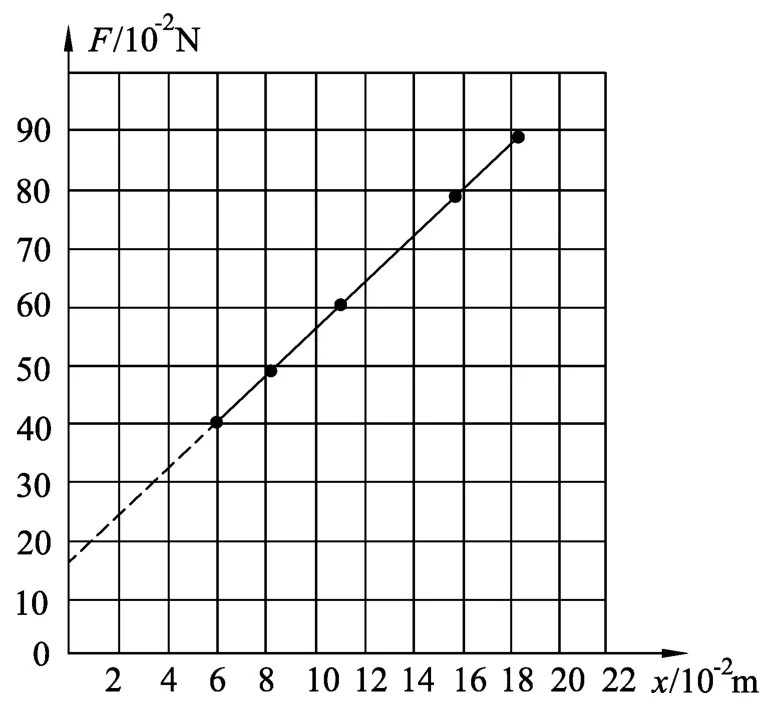
图2 弹簧弹力与弹簧伸长的关系图

图3 密绕圆圈紧贴弹簧（本文简称为密绕紧贴弹簧）

3 问题的分析与实验研究

3.1 理论分析和猜想

在密绕圆圈（非紧贴）弹簧中，弹簧的形变涉及拉伸，弯曲和扭转，其中扭转起主要作用，其他的可以忽略不计.［2］扭转形变实质上是由剪切形变组成的.用圆柱体扭转形变的基本公式可以推导得到密绕圆圈（非紧贴）弹簧所受拉力F与伸长量x的关系为

其中N为材料的剪切模量，R为弹簧金属丝的半径，n为弹簧的匝数，r为弹簧的半径，x为弹簧的总伸长量.

（1）式的推导是基于弹簧线圈之间非紧贴的情况展开的.对于密绕紧贴弹簧则不一定试用.

在图2所示的弹力与形变量的关系图中，截距不为0，图像的直观解释可以为“表面形变量”为零时，弹簧中仍然有弹力，说明弹簧仍然有收缩趋势.

工业生产中，弹簧钢的压力加工方式有热轧、冷拉，锻制等，热处理方式有 “去应力处理”、“不处理”等.不同的加工和处理方式造成弹簧钢的应力性能差异较大，同理会影响到最终成品弹簧的性能.例如，金属丝在冷弯曲成形螺旋弹簧后会产生很大回弹.［3］

笔者做了如下猜想，对成品弹簧而言，存在着“表面形变量”为0，但弹簧内部仍然有（剪切）应变的可能，导致剪切应力不为0，弹簧仍然收缩的趋势.宏观上，有收缩趋势的相邻弹簧圈接触在一起，因挤压产生的额外弹力阻碍了弹簧的进一步收缩，达到了力学平衡.

3.2 设计实验进行验证

为了证明猜想的正确性，笔者设计了如图4所示的装置进行验证.

图4 改进后的实验装置图

3.2.1 实验器材

实验用到的器材主要有（朗威）DIS实验系统（含力传感器、位移传感器），弹簧，铁架台、铁夹等.

3.2.2 实验装置搭建的步骤及主要原理

（1）在铁架台上固定力传感器.

（2）在力传感器下方悬挂待检测弹簧，进入软件界面，在弹簧自然悬挂状态下对力传感器调零.

（3）将位移传感器发射端固定在铁夹上（后面称此为铁夹1），同时将弹簧下端挂在铁夹1上.调节铁夹1的高度，当力传感器的示数从正数（测拉伸力）恰减小为0时，固定铁夹1.之后实验时力传感器的示数即为外界对弹簧的拉力F.

（4）将位移传感器接收端固定在另一个铁夹上（后面称此为铁夹2），调节铁夹2，使得位移传感器接收端与发射端正对，当位移传感器示数为0时固定铁夹2.之后实验时位移传感器的示数等于弹簧的拉伸量x.

（5）点击开始记录按钮，旋松铁夹1的螺丝，使得铁夹1（连同位移传感器）缓慢下降.多次采集力和位移数据并分析.

（6）更换其他疑似问题弹簧，重复上面的步骤.

3.2.3 实验数据分析

将疑似问题弹簧的F、x数据画散点图进行分析，均得到了如图5所示的图像.

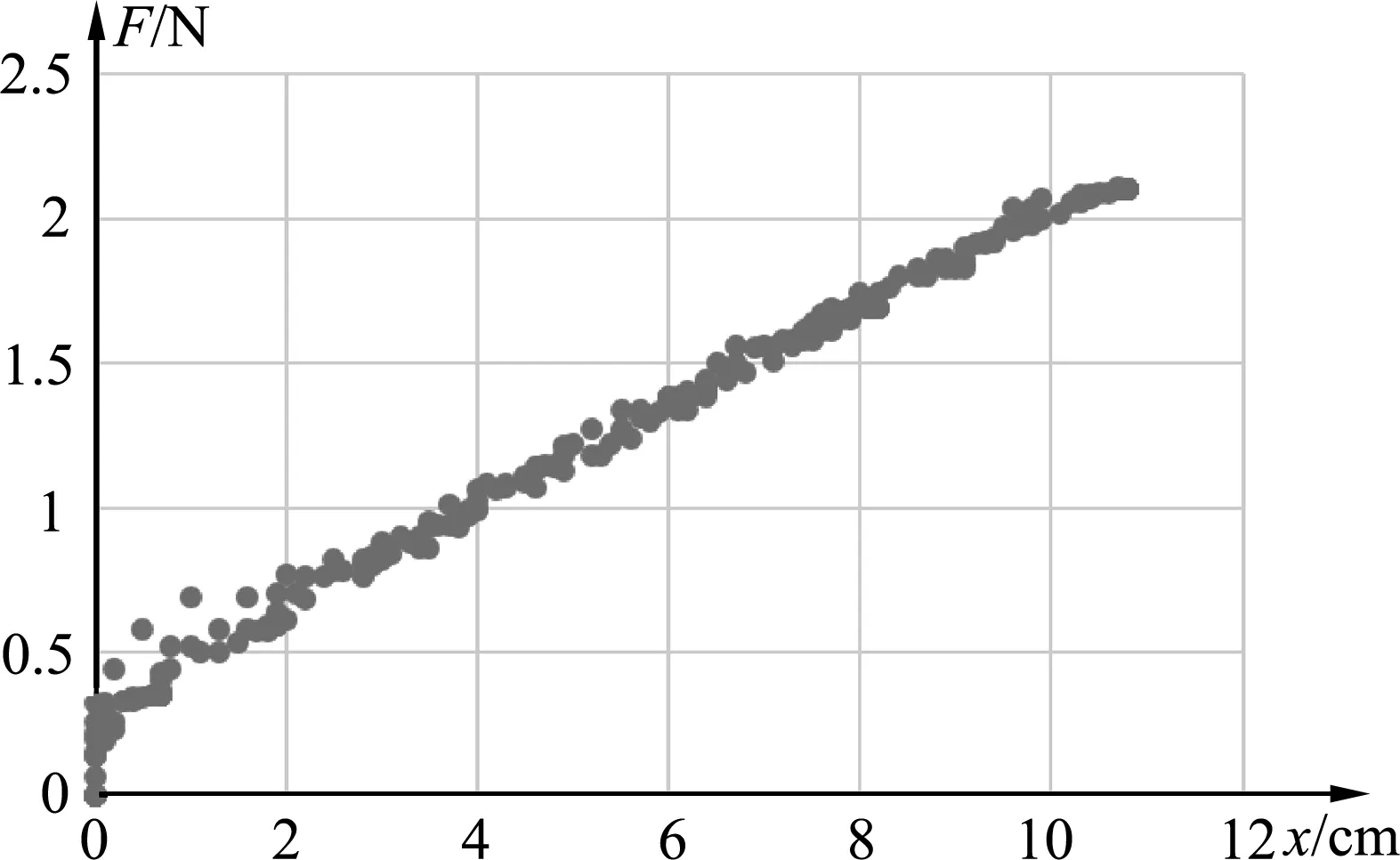
图5 疑似问题弹簧的F、x数据散点图示例

从图5可以看到，在x=0时，存在多处拉力F不为0的位置，这与预期的结果一致，即此弹簧存在初始收缩力F0.当弹簧受到的拉力小于F0时，弹簧并不会被拉伸，弹簧下端的位移为0.图5中的初始收缩力约为0.27 N.

对于存在初始收缩力的弹簧，即密绕紧贴的弹簧，当弹簧受到的拉力大于F0时，弹簧才能被拉伸.由图5可知，此时弹簧下端点施加的弹力，等于受到的拉力F，并不与弹簧形变量x成正比，而是要扣除F0后才能与x成正比.其数学表达式为F-F0=kx，即对于密绕紧贴的弹簧，弹力F与形变量x成线性关系，而不是正比关系.

4 通过修正弹簧解决问题

4.1 修正弹簧的意义

在实际使用中，很多情境下，弹簧弹力F与其形变量x成正比是必须要满足的先决条件，例如“制作弹簧测力计”.对于初学胡克定律的中学生而言，相比于使用“F-x仅满足线性关系的弹簧”，使用“F-x满足正比关系的弹簧”在理解胡克定律的时候显然会更容易些.

而对于“仅满足线性关系的弹簧”，搁置、丢弃显然是资源的浪费，与环保价值观不符合.

如果能将“F-x仅满足线性关系的弹簧”转变为“F-x满足正比关系的弹簧”，将显著提高资源的利用率，降低学生学习过程中不必要的干扰因素.

4.2 修正弹簧的方法

在工业生产中，使用机械拉伸法可以去除材料内的应力，［4］即用部分塑性应变抵消部分弹性应变.根据这一原理，采用如下方法修正弹簧.

（1）测量弹簧拉伸前的原长，设为L0.

（2）手持弹簧的两端，增加拉力，拉伸弹簧至长度为原长的2倍，即2 L0后，减小拉力，使弹簧恢复到自然伸长状态，测量此时弹簧的长度，设为拉伸释放后弹簧的原长L.

（3）如此往复，分别拉伸弹簧至3 L0，4 L0，5 L0…直至拉伸释放后弹簧的长度为L与弹簧的拉伸前原长L0不一致，即发生范性形变时停止拉伸.例如L比L0大1 cm时结束拉伸，弹簧修正完毕.如图6所示，将某弹簧拉伸至原长10倍长度后释放，原长比拉伸前增加约1.6 cm.

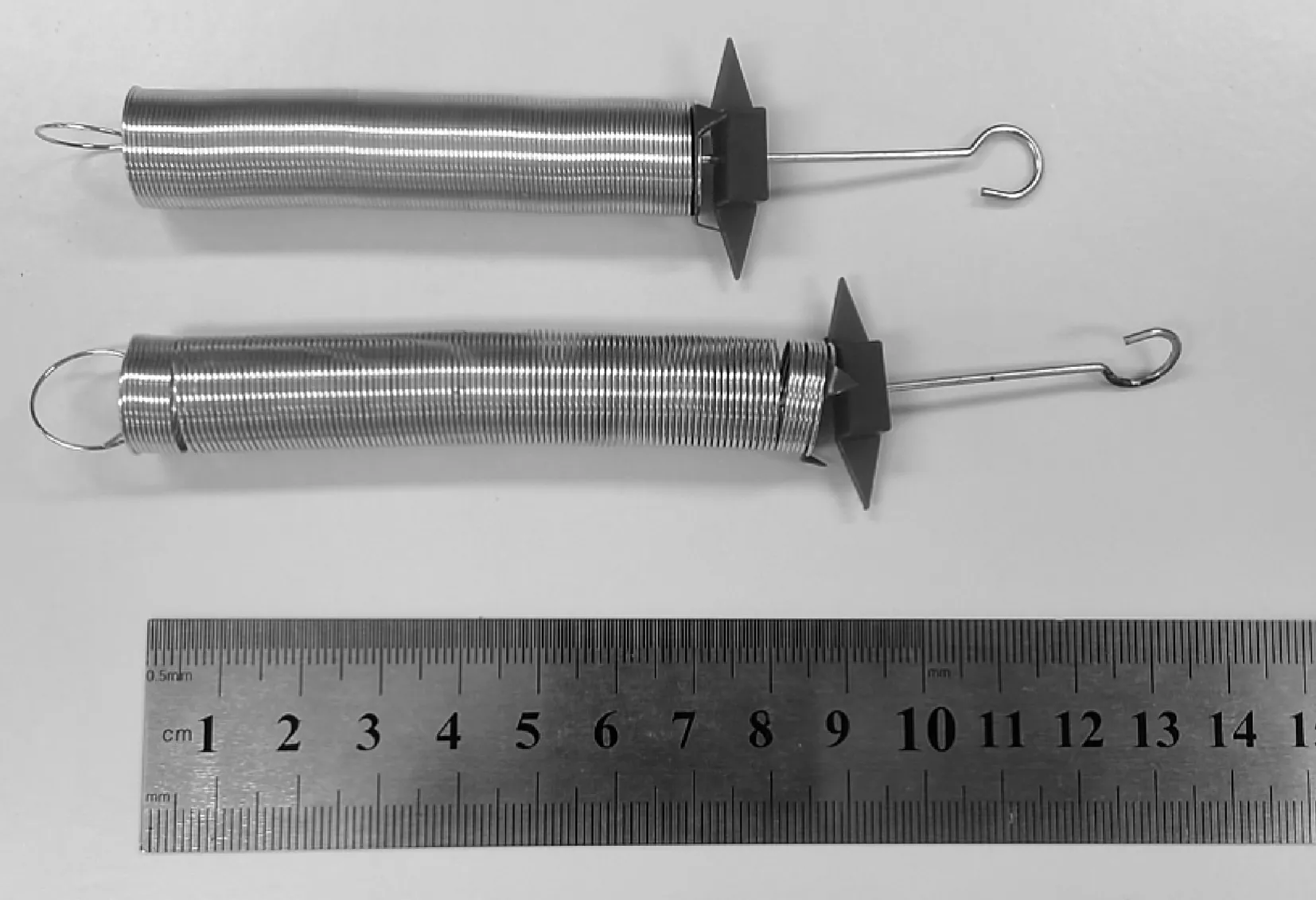
图6 同规格的两个弹簧在拉伸前后的对比图（上方为未拉伸时候的状态，下方为10倍拉伸释放后的状态）

4.3 修正后弹簧的表观特征

与修正前相比，修正后的弹簧，表观上，弹簧相邻金属圈之间不再紧密接触，有了肉眼可见的缝隙甚至是明显分离，轻拉弹簧后释放，能够看到弹簧的细微振动.

4.4 修正弹簧的检验

修正弹簧的目标是为了将“F-x仅满足线性关系的弹簧”转变为“F-x满足正比关系的弹簧”.为此需要检验修正后的弹簧 “弹力与形变量是否满足正比关系”.

4.4.1 被检验弹簧的一些参数

笔者选取了4种规格的“问题弹簧”，修正前，其弹力与形变量均不满足正比关系，但满足线性关系.被检验弹簧的拉伸前后的参数如表1所示.

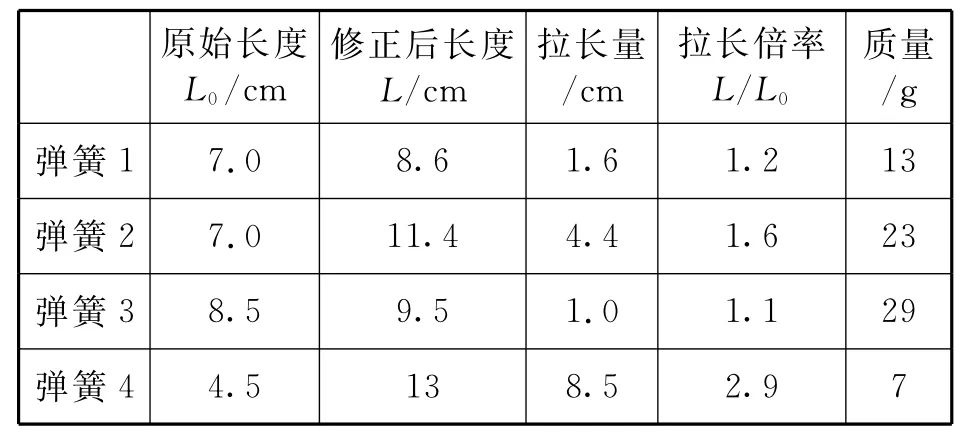
表1 4种被检验“问题弹簧”的参数

4.4.2 检验方法和检测结果

用图4所示装置，采集“问题弹簧”在修正前后的弹力F和形变量x数据，绘制F-x图，进行对比分析.F-x图对比示例如图7所示.

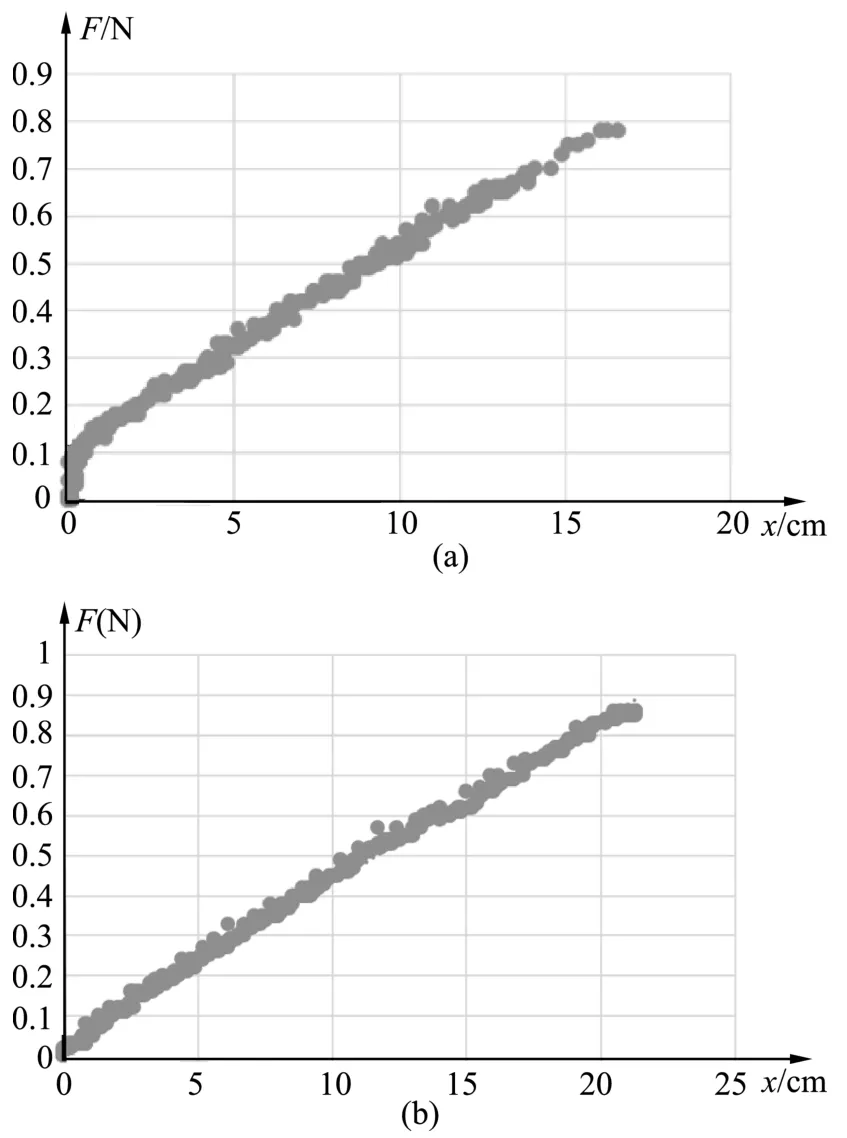
图7 弹簧1在修正前后的F-x图（a）为未拉伸时，（b）为拉伸修正后.

满足胡克定律的弹簧，F-x图中直线斜率为弹簧的弹性系数k.

对各“问题弹簧”修正前的F-x图中的直线部分进行线性拟合，自变量x前的系数仍具有弹性系数的量纲和意义，在此仍旧称为弹性系数k.线性拟合后，纵轴截距对应于形变量为0时的弹力，在本文称之为初始收缩力F0.

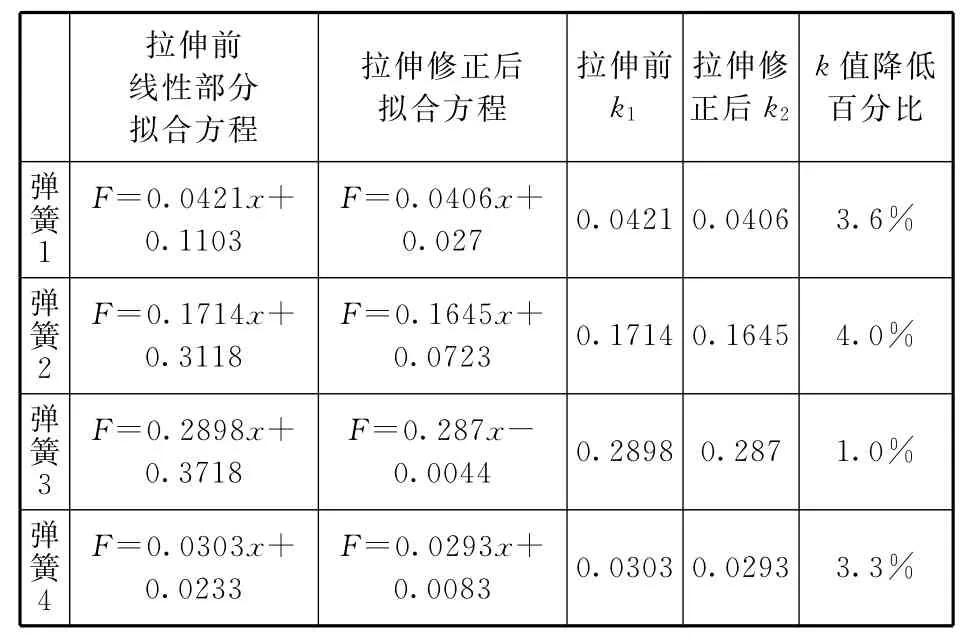
表2 4种被检验“问题弹簧”在拉伸前后的F-x图拟合方程及数据分析

4.4.3 检测结果分析

从图7可以看出，修正后的弹簧，弹力F与形变量x满足良好的正比关系.

对比表2中拟合方程的截距可以看出，修正后，截距几乎降为0，即通过拉伸，良好地消除了“问题弹簧”的初始收缩力F0.

通过表2中的弹性系数k的变化可以看出，拉伸后弹簧的k值都略有下降，但k值降低百分比较小，在笔者的实验中，k值降低百分比都在4%以内.

4.5 实验结论

可以通过“拉伸法”对密绕紧贴弹簧进行修正，“拉伸法”能降低密绕紧贴弹簧的初始收缩力.在一定范围内，修正后的弹簧仍具有良好的弹性，并且，弹力F与形变量x能够满足良好的正比关系.