运用等效思想 突破复杂情境

张国泉

（南京师范大学附属中学，江苏 南京 210003）

《普通高中物理课程标准（2020修订版）》在教学与评价建议部分指出：“评价的任务情境要有一定的问题性、真实性、探究性或开放性，通过学生在应对复杂的问题情境，参与相应的探究学习活动的表现中来考查物理学科的核心素养”.在历年的高考题中，就有很多试题的问题情境非常好的体现了上述要求，细细品味，别有韵味，例如2010年江苏省高考物理试卷的最后一题.该题以制备纳米薄膜为背景情境，给出随时间周期性变化的电压，进而对带电粒子在电场中的运动进行了深入考查.本题的新颖之处在于在一个周期内的前半个周期的电压值和后半个周期的电压值并不相等，大大增加了问题解决的难度.本刊2010年第10期《巧解2010年江苏高考物理试题》一文中给出了归纳的方法、2011年第2期《2010年江苏高考物理卷压轴题解法探析》一文提出了另外几种方法，但出发点都是直接在题目给出的电压的基础上受力分析，并结合牛顿运动定律或功能关系求解的.这些方法的数学计算量均偏大，对学生来说，较难在考试中有限的时间内求得正确结果.但若运用等效思想将该题中给出的信息先加工处理一下，就能够变复杂为简单，且更好地与学生熟悉的情境结合起来，从而大大降低计算的繁琐程度，有利于学生能够在较短的时间内突破解决问题.下面给出具体的处理思路和方法，并谈谈自己的反思体会.

1 原题再现

例题.制备纳米薄膜装置的工作电极可简化为真空中间距为d的两平行极板，如图1（甲）所示.加在极板A、B间的电压UAB做周期性变化，其正向电压为U0，反向电压为-kU0（k＞1），电压变化的周期为2τ，如图1（乙）所示.在t=0时，极板B附近的一个电子，质量为_m、电荷量为e，受电场作用由静止开始运动.若整个运动过程中，电子未碰到极板A，且不考虑重力作用.

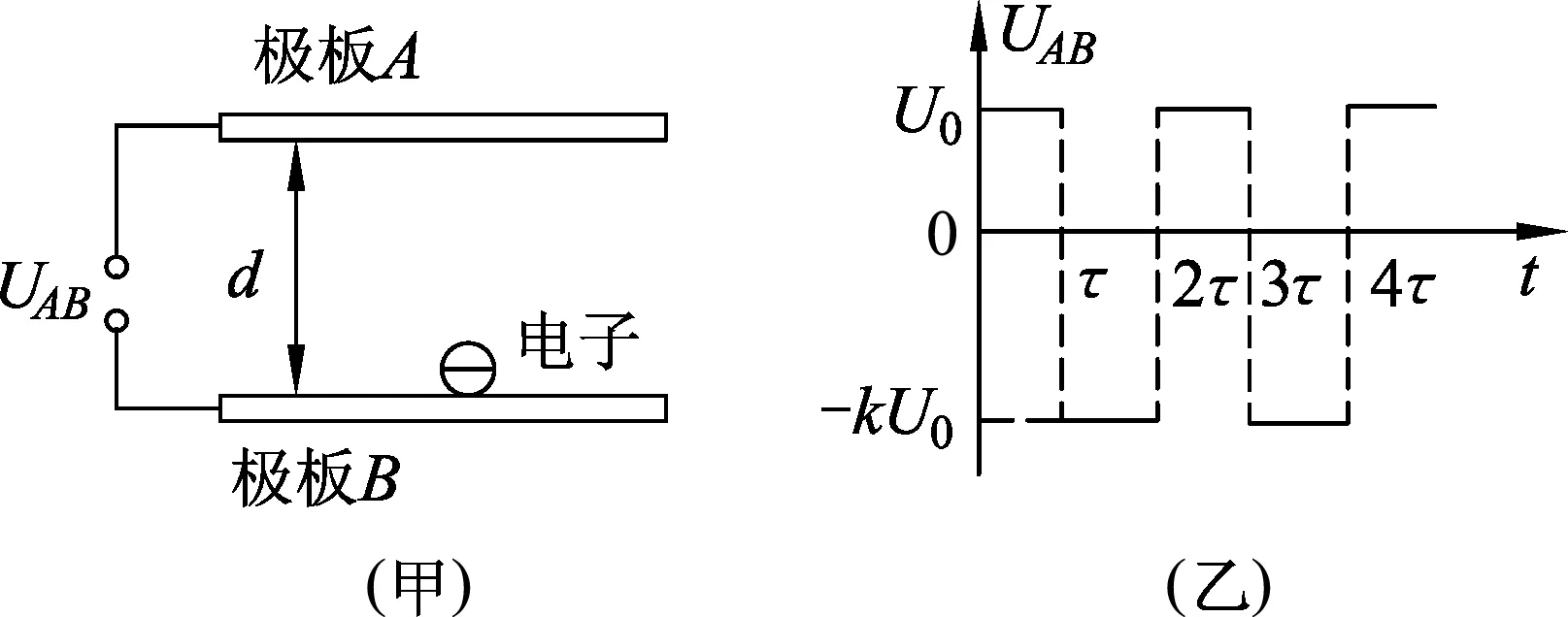
图1

（2）若电子在0～200τ时间内未碰到极板B，求此运动过程中电子速度v随时间t变化的关系；

（3）若电子在第N个周期内的位移为0，求k的值.

2 试题分析

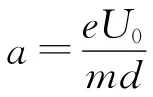
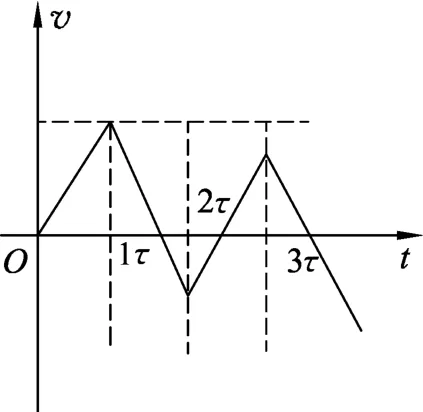
图2

3 突破方法

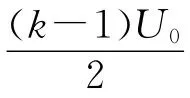
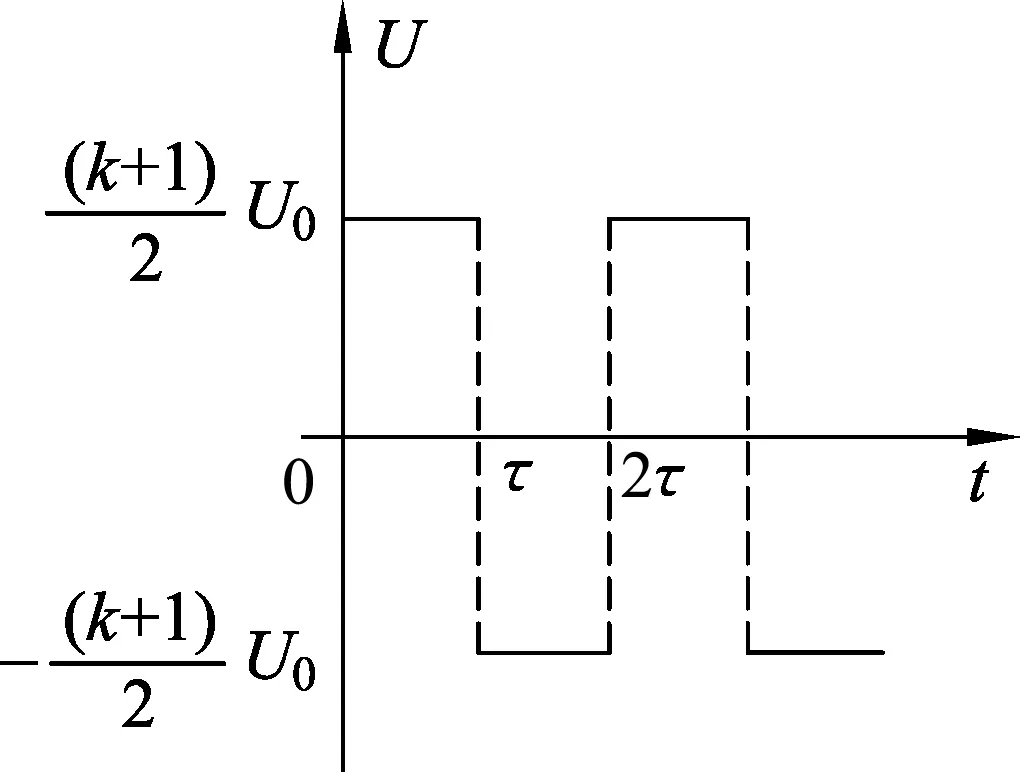
图3

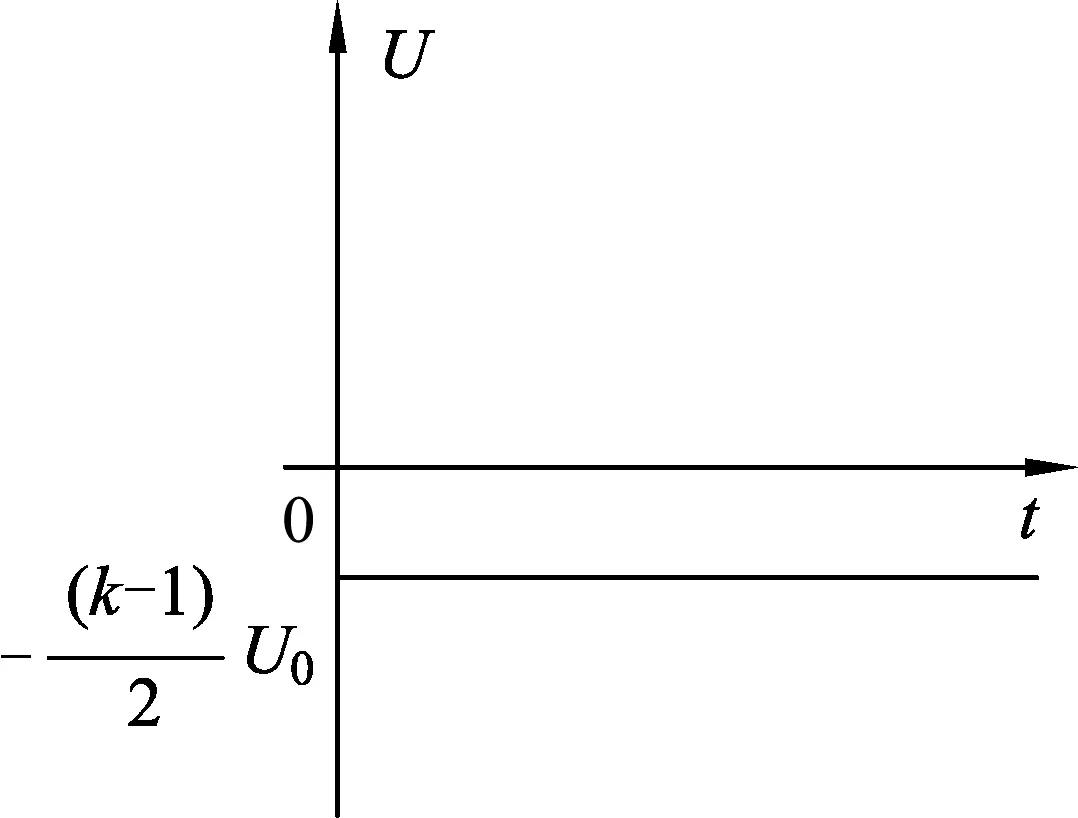
图4

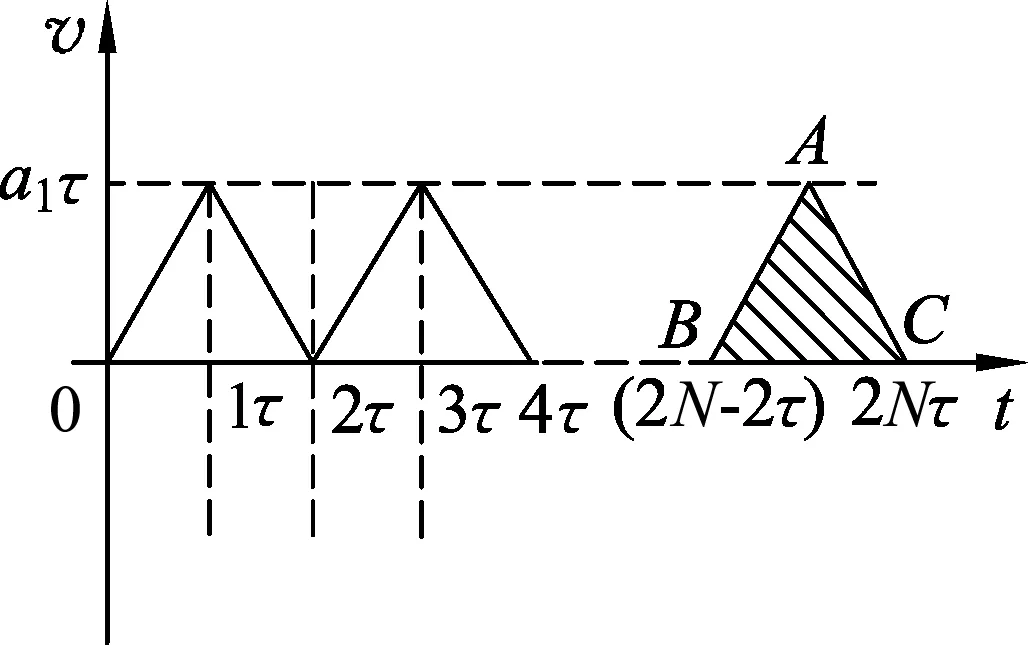
图5

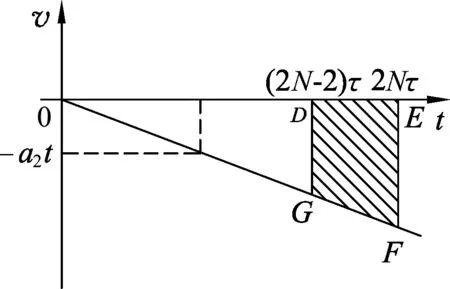
图6

Ⅰ.试题的第（2）问：某一时刻电子速度即为这两个运动的速度的矢量和.

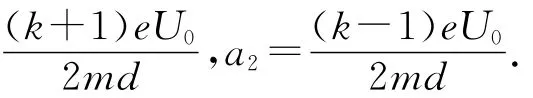
考虑到任意时刻t运动①和运动②的速度方向都是相反的，因此有

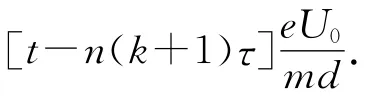
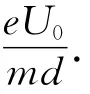
式中n=0、1、2、…99.

Ⅱ.试题的第（3）问：由图像可知，运动①在第N个周期内产生的位移大小为图5中三角形ABC的面积S1，运动②产生的位移大小为图6中梯形DEFG的面积S2，而这两个位移的方向相反，所以要使得电子在第N个周期内的总位移为0，只要S1、S2相等即可.

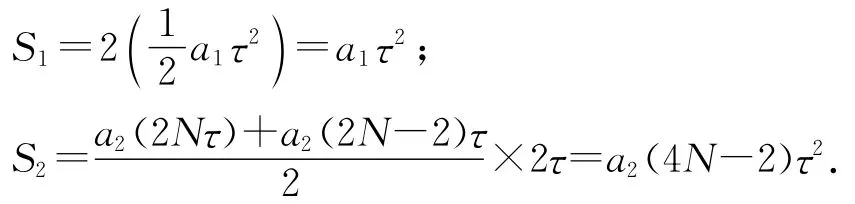
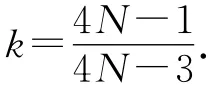
4 反思体会

等效替代思想是物理学中非常重要的思维方法，因为自然界的物质的运动、构成及其相互作用都是很复杂的，人们往往从事物的等同效果出发，将其转化为等效的、简单的、易于研究的物理事物进行研究.比如在解决这道高考题时，实际上是将原电压（电场）的作用等效为两个电场的作用，进而将电子的运动等效为的两个相对简单的、熟悉的运动的合运动.在高中物理中有很多涉及这种思想方法的地方，大致可分为模型的等效替代（例如卢瑟福的核式结构模型）、作用的等效替代（例如力的合成与分解、交变电流的有效值）、过程的等效替代（例如平抛运动可等效为在相互正交的两个方向上的直线运动的合运动、简谐运动可等效为匀速圆周运动在通过圆心的一条直线上的投影）、物理规律的本质的等效替代（例如判断感应电流方向的右手定则和楞次定律本质是等效的、热力学第二定律的开尔文表述和克劳修斯表述本质是等效的，即一切与热现象有关的宏观过程是不可逆的）.在我们的教学过程中，应该有意识地渗透相关的思想方法，进而将核心素养的培养真正落到实处，进一步提高学生面对复杂问题情境时的解决能力.