用“逐帧法”解决初中光学问题的案例分析

李 啸 李 刚

（1.南京师范大学附属苏州石湖中学，江苏 苏州 215299；2.苏州市教育科学研究院，江苏 苏州 215004）

在初中光学教学实践中发现，大部分简单光学问题都能利用光的直线传播特点、光的反射定律与光的折射规律快速解决，但有些题目由于光路传播较复杂，初中生的逻辑分析，推理能力相对薄弱，所以初中物理教师需要寻求“方法”或“策略”来帮助学生.本文针对初中物理中一些涉及传播较复杂的光学问题，采取Flash制作中添加帧图像方式，将复杂过程逐一分解，在具体、形象的基础上再抽象出可见的“图式”供学生思考，从而提升学生的思维品质.

例1.如图1所示，平面镜OM与ON镜面之间的夹角为α，在两平面镜角平分线上有一个点光源S，如果要保证S发出的任意一条光线最多只能产生两次反射，则α的最小值是

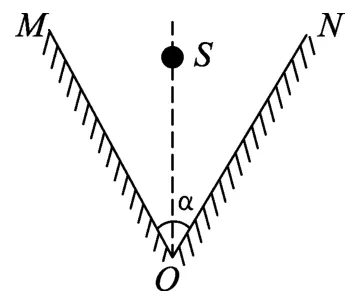
图1

（A）120°. （B）90°. （C）72°. （D）60°.

笔者按照常规解法，将图1的情境转化为图2所示的模型图景，由于题目中要保证S发出的任意一条光线最多能产生两次反射，也就是说点光源S在平面镜中只能2次成像，在OM镜后第1次成像，像点为S1，像点S1紧接着在平面镜ON后成像S2，为保证不会反向成像S3，像点S2必须要落在MO的延长线上才不会第3次成像.当讲解到这时，笔者请班上听懂的学生举手，结果只有2名学生举手，其他学生感到茫然，于是笔者在黑板上又画图解释点光源经过平面镜多次反射光路图，学生还是感到困惑，僵局如何突破？

图2

这时一位学生提出了另一种巧妙方法，笔者邀请该生为大家讲解.只见这名学生在黑板上画出如图3所示的光路图，设入射光线SA与平面镜MO夹角为β，则反射光线AB与平面镜MO夹角也为β.当第2次反射时，原来的反射光线AB即为入射光线，则AB与平面镜NO的夹角为180°-α-β，同理SB与平面镜NO夹角也为180°-α-β.如果SB平行于MO，则α=180°-α-β，即β=180°-2α.如果B点越靠近O点，α＞180°-α-β，则不会出现第3次反射，即β≥180°-2α.似乎学生们听懂了，班里响起了热烈的掌声，但笔者问该生，你怎么知道一定要画该图形？该生说只是做过此类题，记住了该图形.看来，这种解法只是个案，这种片段性光路解析往往会阻碍学生思维发展.

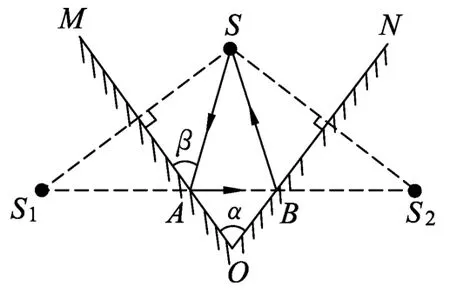
图3

怎样使个案解法具有普遍性，打破片段性光路的局限，笔者尝试利用给定的特殊角度制作Flash动画，通过运行动画让学生深刻理解斜镜中的反射情况.如图4所示，在夹角为90°的两块镜面中，取角平分线上的点光源S发出的任意光线按照第1帧、第2帧、第3帧顺序播放，学生发现除第2帧反射光线原路返回，只发生了1次反射外，其他情况均发生了2次反射.由于镜像对称，点光源S有3个虚像，但点光源S相对于两个镜面先后只成2次像.

图4

由第1个动画可以总结出：S发出的任意1条光线最多只能产生2次反射，则要求点光源S在平面镜中只能成2次像，这是一个严格而又苛刻的条件.进一步发问：是不是90°的角就是α的最小值？学生愈发感兴趣起来，教师继续探究.如图5，6所示，再次利用Flash动画，添加关键帧，运行Flash对72°角进行探究如下.

图5

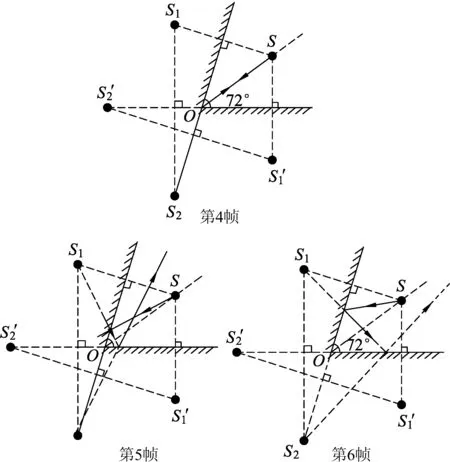
图6

两镜面夹角为72°时，点光源在两块镜中分别成像S1点和S1′点，2次成像点都位于第1块镜面的延长线上，即满足点光源S在平面镜中只能2次成像条件.如图5第2帧不难发现与图3对应的图景一样，旨在让学生认识到局部来源于整体，任何解题思路的诞生都源于对原生态的挖掘过程.

当播放到第5帧时，学生发现点光源S发出的光越靠近O点，2次反射出来的光近似于镜面平行，而远离O点，光线向右侧发散程度越大.通过完整运行，学生对72°角斜镜反射问题有了深入了解，再结合角镜成像个数经验公式n=360°/θ-1可以顺利排除答案（A）与（D）.

例2.如图7所示，平面镜和凸透镜的主光轴垂直并处在凸透镜两倍焦距处，在凸透镜的另一侧两倍焦距处有一个点光源S.现将平面镜向凸透镜靠近的过程中，讨论点光源所成的像.

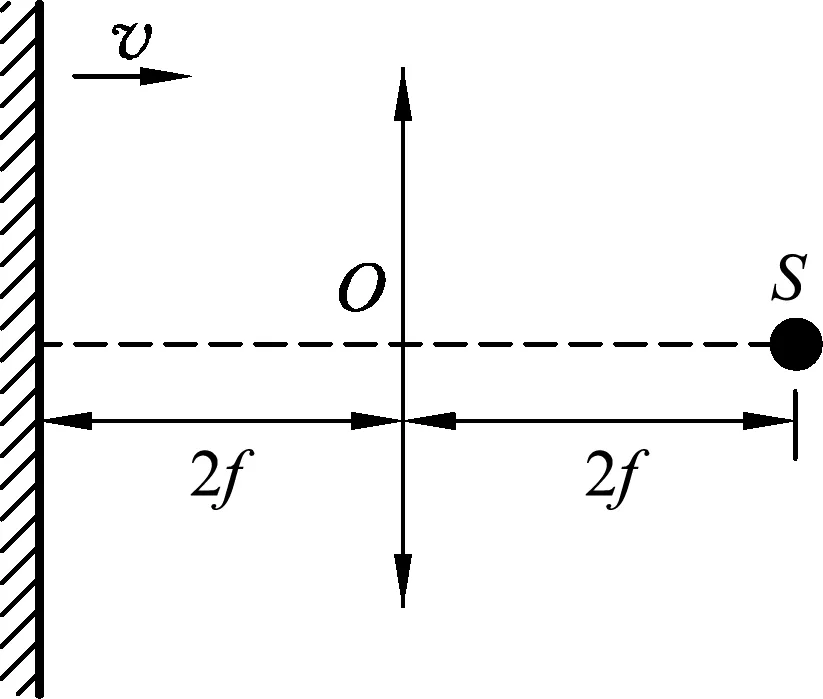
图7

该试题中既涉及到光的反射又涉及到光的折射，作图需要利用焦平面作图法.对于动态光路变化，解决问题的关键是厘清光路改变与平面镜的位置关系，所以需要运动过程中对每一个环节进行探析.由于学生的想象力不足以在短时间内描绘出每一个环节的具体情境，这时不妨借助例1中的“帧”分解法，对整个过程进行分解，再从局部到整体，快速帮助学生厘清两者变化关系，如图8所示.

第1帧中，点光源S发出的光经过凸透镜折射后在平面镜与主光轴交点处成实像点S1，再经过平面镜反射和凸透镜折射后在S处又形成一个实像S2.

第5帧中，当x=f，经平面镜反射的光线恰好过光心，不成像.

图8

第6帧中，当f＜x＜2f，经平面镜反射的光原本应成在S1处，但由于凸透镜折射，成像在S1的左侧S2处（只有一个实像，没有虚像）.

解答过程中，以“帧”展现过程的同时，清晰描绘出光的反射与折射的动态变化图景.学生利用形象、直观的演示理解起来变得容易一些.这种方法将动态过程“微分”成特定的“帧”，以“帧”所代表的特点来寻找光现象中蕴含的规律，教学过程中把形象思维与抽象思维高度协调在一起，使思想有了形象的基础，又有了抽象推理的逻辑过程，较好提升了学习的品质.

上述通过教学实践的2个案例分析说明了运用“逐帧法”不仅可以解决运动学问题，也可以在初中光学中大放光彩，其蕴含的物理思维是独特的“分解”与“微分”思想.这种思想在高中物理教学中也有着独到的应用.教学中通过这种思维方法的训练，可以潜移默化让学生体验到物理思想方法在解决实际问题中的应用，提升学生思维能力与思维品质.