考虑转子异步损耗的永磁同步电机高效率控制研究

肖仁鑫，李 烜，胡海双

(1.昆明理工大学 交通工程学院，昆明 650500；2.昆明物理研究所，昆明 650000)

0 引 言

永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)效率和功率密度高、转动量小、动态响应快，因此广泛用于伺服系统、电动汽车的驱动和工业等场合[1-2]。资源短缺和环境压力逐渐加剧，永磁同步电机设计和应用更加趋于小型、高效和低耗，因此电机的控制需要快速性和鲁棒性。在汽车驱动过程中，驱动电机需要在整个转速区间高效率地工作，从控制的角度提高电机工作效率，需要降低电机可控损耗，主要包括铜耗和铁耗[3]。电机转子的铁心会产生涡流损耗和磁滞损耗，这些损耗会长期积累加剧转子永磁体的损耗，使电机性能下降[4]。

传统控制策略在基速以下PMSM采用单位电流转矩最大(Maximum Torque Per Ampere, MTPA)策略，它只考虑了铜耗[5]，基速以上，采用单位电压转矩最大(Maximum Torque Per Voltage, MTPV)策略[6]，只考虑了铁耗[2]，二者都不能实现给定负载下的电机效率最优。

电机损耗最小方法(Loss-Minimization Algorithm, LMA)可以进一步提高电机的工作效率[7]，LMA策略可分为损耗模型控制(Loss- Model Control, LMC)、搜索控制(Search Control, SC)和混合控制(Hybrid Control, HC)。LMC一般建立PMSM的电机损耗模型，求取使铁耗和铜耗最小的直轴电流[8]。文献[9]对损耗模型进行了简化，这些方法主要运用在基速以下，没有对基速以上区域的工作效率优化进行讨论。SC不需要建立电机损耗模型，在给定负载和转速下，迭代搜索使目标函数最小的控制变量[10]，不受电机参数的影响，常用黄金分割、斐波那契等搜索法，每次迭代搜索需要采样，收敛较慢，且容易引起转矩和转速的振荡。

计算PMSM的铁耗，主要有磁滞损耗、涡流损耗和部分附加损耗组成。龚宇[11]等人把电机的铁耗从空载损耗中分离出来，通过雨流计数法计算磁滞损耗，但没考虑转子涡流损耗。文献[12]提出一种基于穿透深度的涡流损耗分析方法,通过有限元计算分析出对转子永磁体涡流损耗的影响因素。赵祥，范瑜[13]等人提出了单层分数槽集中绕组永磁同步容错电机的转子模块化结构，减小了转子涡流损耗。文献[14]考虑谐波因素建立了场—路耦合有限元模型，获取最优开关频率减小转子涡流损耗。通过以上文献的研究成果可以分析出转子损耗对电机效率影响非常大。

电机在起动、急停、加速减速状态时，电机处于异步状态，此时转子上有异步损耗[15]。通常铁耗计算主要考虑在电机同步状态下高频异步损耗，而对异步状态下转子异步损耗考虑较少，同时，对于电动汽车驱动用PMSM，由于汽车频繁起停、加速减速等动态工况，会使驱动电机频繁工作在异步状态下，此时的转子异步损耗会造成转子发热而引起退磁，电机性能下降甚至导致故障，针对这一问题，本文提出了一种考虑转子异步损耗的最小损耗控制，基于损耗模型，在线搜索最优磁链的方法，通过数值计算法可以快速求解目标函数而不引起转矩的振荡，从而实现电机在全工况下的高效率控制。

1 考虑转子损耗的PMSM损耗模型

异步转子涡流损耗的PMSM在d-q轴坐标系下的损耗模型如图1所示。

图中Rs为定子电阻，Rc为定子铁损电阻,Re为转子铁损电阻,L1s为定子磁漏,Lmd为直轴励磁电感,Lmq为交轴电感，定子d、q轴电感为Ld=Lmd+L1s、Lq=Lmq+L1s；φd、φq分别为定子d、q轴磁链,ψd、ψq分别为转子d、q轴磁漏，ωe为同步电气转速，ωr为转子电气转速;同步状态下ωe=ωr,ωf为异步电气转速，且ωf=ωe-ωr，同步状态下，ωf= 0，此时等效电路模型等价于传统的只考虑定子铁损的等效电路模型,ud、uq分别为d、q轴定子端电压，idc、iqc分别定子d、q轴铁损电流，iod、ioq分别定子d、q轴励磁电流,ide、iqe分别转子d、q轴电流，if为永磁体等效励磁电流，永磁体磁链φf=Lmd×if，考虑永磁体为磁源，忽略转子上的磁漏。

在d-q轴坐标系中，PMSM的电压方程可表示为

(1)

等效磁链表达式为

(2)

定子电流表达式为

id=iod+idc、iq=ioq+iqc

(3)

定子铁损支路电流表达式为

(4)

由上述磁链表达式和定子电流方程代入电磁转矩方程，通过合并化简得到：

(5)

式中，pn为极对数，等号右边括号中第一项为输出电磁转矩Te，第二项为定子铁损转矩，第三项为转子铁损转矩，令输出电磁转矩Te为

(6)

其中，输入有功功率为

(7)

式中右边第一项和第二项分别为定子铜损(Pcu)和铁损(PFe)，第三项为转子损耗，第四项为输出电磁功率，包含机械损耗及杂散损耗。

电机输出功率为

P*=Teωe

(8)

故电机的效率为

(9)

2 基于损耗模型的PMSM最优磁链控制原理

在给定转矩转速下，忽略定子电阻上压降时，求解需求电压可有方程组(10)求解，该方程由转子电压微分方程10(a)、10(b)，转矩方程10(c)与定子磁链方程10(d)的代数方程组成的微分-代数方程组。

(10)

直接求解微分-代数方程组难于得到解析解，即使在忽略微分项时求得的解也过于复杂，不利于在电机实时控制系统中实现。为求解该方程组，采用同步—异步数值迭代的方法求解。

2.1 同步状态下求解

在同步状态下,ωf=0，则ide、iqe均为0，可直接求解代数方程为

(11)

在忽略定子电阻上压降时，求解定子需求磁链ψs，令

Z1=φf+(Ld-Lq)iod

(12)

将式(12)代入式(11)并整理得：

(13)

式中，

由于此时只有Z1包含变量iod，在a处将方程右边进行一阶泰勒展开：

(14)

将式(14)代入式(13)得：

(15)

化简求得其近似方程解：

(16)

代入式(12)可求得iod、ioq的解：

(17)

(18)

本文搜索最优磁链运用黄金分割算法，使用额定磁链给出初值搜索区间，计算不同的转矩、转速下的输入功率并比较大小，根据比较结果，去掉额定磁链范围左端点或者右端点，按照上述步骤进行下一次迭代，缩短搜索区间，接着在减小后的区间上做相同的搜索，不断进行迭代，缩短搜索区间，直到满足精度要求为止，求解出满足此时转矩、转速输入下的最优磁链。进而可求出此时最优d轴电流，其整体控制流程如图2所示。

图2 同步计算时PMSM控制流程

2.2 异步状态下求解

当ωf大于设定门槛时，进入异步求解，假如当前时刻为k，此时iod、ioq采用同步求解最近时刻的值，ide、iqe初始值为0代入式10(a)、式10(b)的差分方程迭代可求k+1迭代的ide、iqe。令：

由式10(a)、式10(b)可得差分方程得，

ide(k)=A1iod(k)+B1ioq(k)+C1iod(k-1)+D1ioq(k-1)+

E1ide(k-1)+F1iqe(k-1)+G1

iqe(k)=A2iod(k)+B2ioq(k)+C2iod(k-1)+D2ioq(k-1)+

E2ide(k-1)+F2iqe(k-1)+G2

(19)

式中，

上式中Δt为差分过程中时间变量，将式(19)代入式10(d)并联立式10(c)可以求解出k+1迭代需求定子磁链下的iod、ioq。令：

Z2=φf+(Ld-Lq)iod

(20)

m=Lmdide、n=Lmqiqe

(21)

故联立式10(c)、式10(d)可得：

(22)

将式(20)代入式(22)可得：

(23)

其中,

与同步求解一样把式d-b/Z22-c/Z2在Z2=-as处进行泰勒展开：

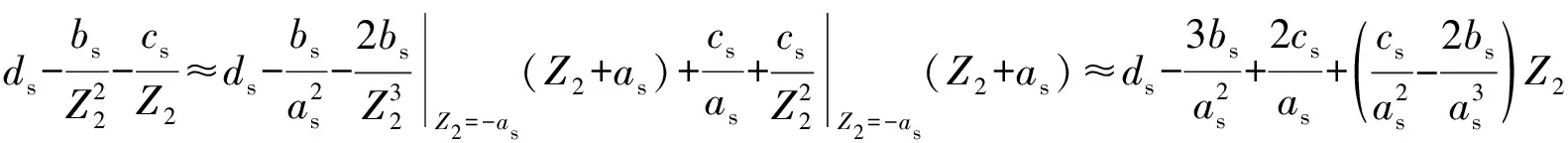
(24)

由式(24)可得：

(25)

化简式(25)求得其近似方程的解：

(26)

将式(26)代入式(20)可求得iod、ioq的解：

(27)

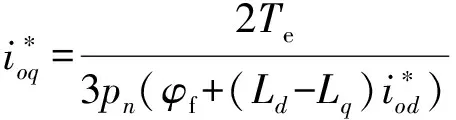
(28)

根据需要，采用k+1迭代的值代入进行下次迭代，求出k+2时刻ide、iqe、iod、ioq。如此往复可以求解出异步状态时给定转矩和转速下定子磁链对应着的iod、ioq、ide、iqe。其整体控制流程如图3所示。

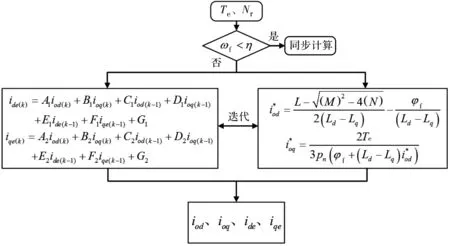
图3 异步计算时PMSM控制流程

图3中,L-N为代数系数，η-临界值。

2.3 转差速度判定

在同步状态和异步状态之间切换，需要计算转差速度，当前的转子速度ωe可由转速传感器得到，定子端的同步速度ωr可以根据电流、电压或磁链相应相位角的微分求得，转差速度ωf为二者之间的差值。图4为仿真过程中计算的ωe、ωr，工况如第四节所示，参数由表1所示。

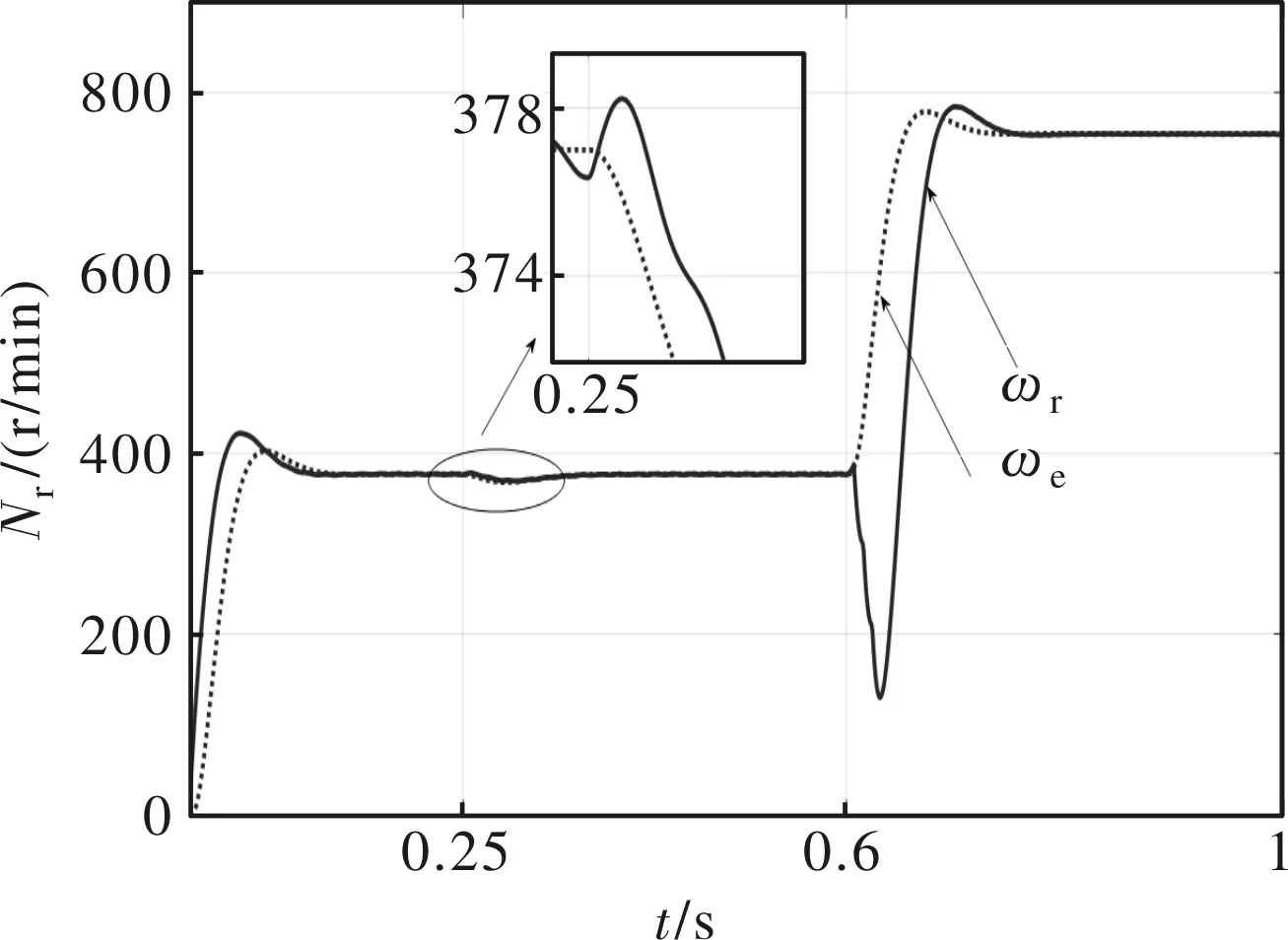
图4 ωe、ωr曲线

3 控制系统的搭建

矢量控制技术是借鉴直流电机电枢电流和励磁电流相互垂直，以坐标变换理论为基础，通过控制定子电流在同步旋转坐标系中的大小和方向，达到对交轴和直轴分量解耦的目的，从而实现磁场和转矩的解耦控制，使交流电机具有类似直流电机的控制性能。

目前传统的矢量控制常见方法有id= 0控制、最大转矩电流比(MTPA)和弱磁控制。为了提升效率，需要根据实时工况对定子电流给定值在线进行调整。在一定工况下一定有一个定子电流值使得PMSM的效率最优。根据以上分析，搭建考虑转子异步损耗的永磁同步电机损耗最小控制仿真模型。

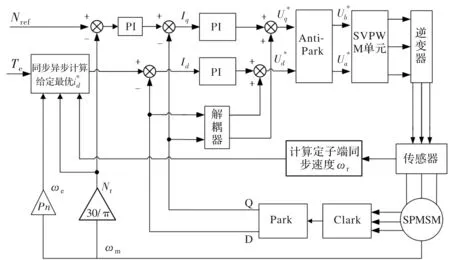
图5 考虑转子异步损耗的PMSM控制流程

4 仿真研究

PMSM参数由表1给出。为了验证所提出的方法的合理性，设计速度控制器参数为kP=0.1、kI=3。

表1 永磁同步电机模型参数

仿真实验：设置了带载起动、稳定运行、低速大负载、加速运行四种工况：初始起动时，电机以2 Nm的负载起动到1000 r/min稳定运行到0.25 s时增加负载到11 Nm并稳定运行到0.6 s时加速到2600 r/min，负载降为4.5 Nm，之后以高速低负载稳定运行，该工况覆盖了起动、稳定运行、加速和负载变化多种工况。工况及其转速响应如图6所示。

图6 工况设置及其转速响应曲线

图6显示了所提策略和传统控制策略(额定转速下MTPA策略，额定转速以上弱磁策略)控制下的转速响应曲线，在0.25 s负载增加和0.6 s时转速增加，转速误差在(-5,5)r/min之间，而传统控制策略转速误差在(-7.5,10)r/min之间，这是由于在动态工况下转矩，采用所提策略转矩脉动减小，如图7所示。

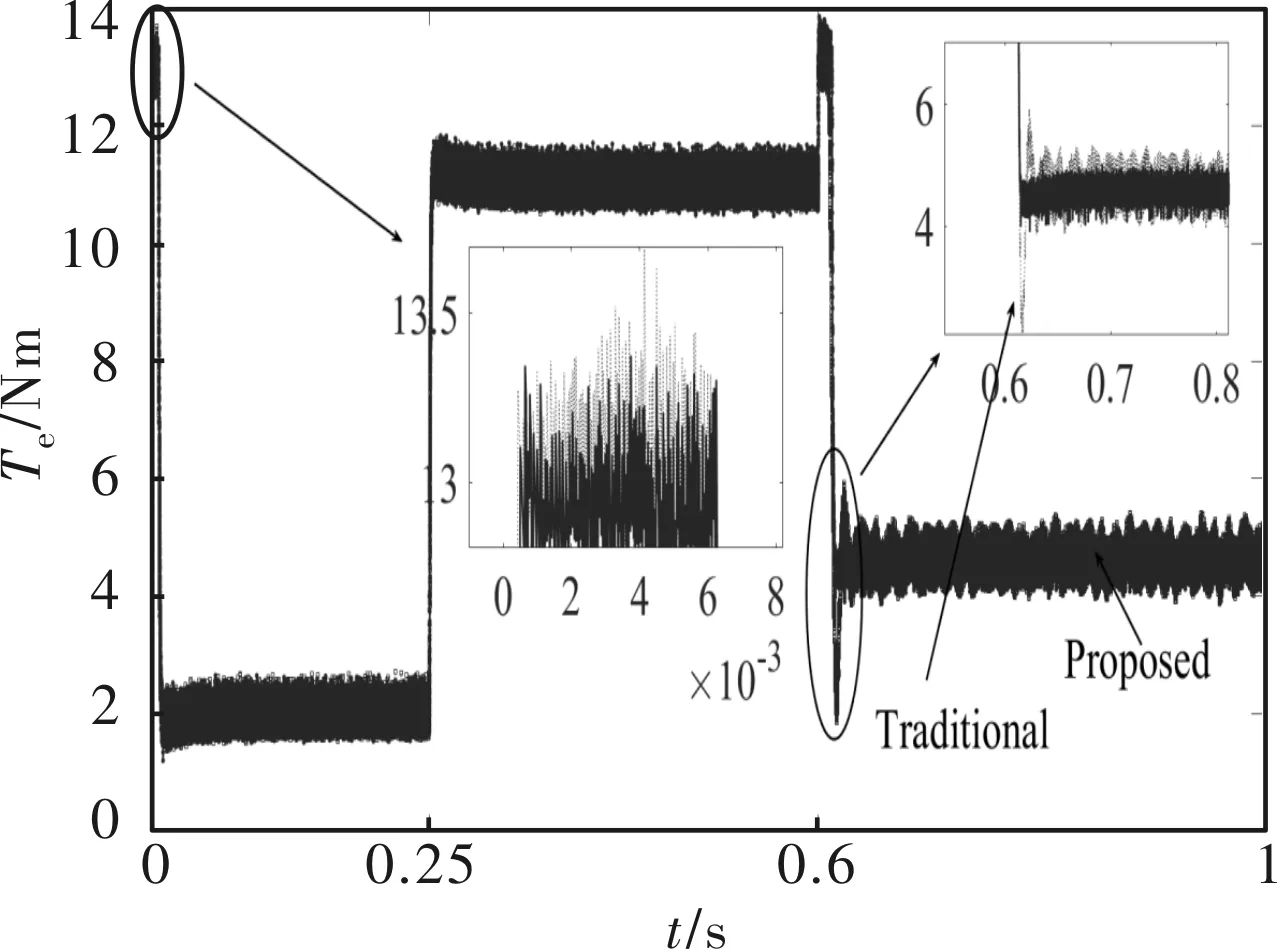
图7 转矩响应曲线

图7的转矩响应曲线表明，在0.6 s转速转矩发生变化时。由式(2)和式(6)可得，本文控制策略模型在此时异步状态下考虑异步转子损耗电流，在母线电压保持不变的前提下，减少定子端铜耗电流谐波，使输出稳定，由式(6)可知电磁转矩由定子端d-q轴电流决定，使转矩响应快、动荡小。如图7可知，在0.6 s时本文提出策略转矩误差在(-0.5,0.5)Nm之间，而传统控制策略转矩误差在(-1.5,1)Nm之间，由此在高速低负载下本文提出的控制策略优于弱磁加MTPA控制策略。

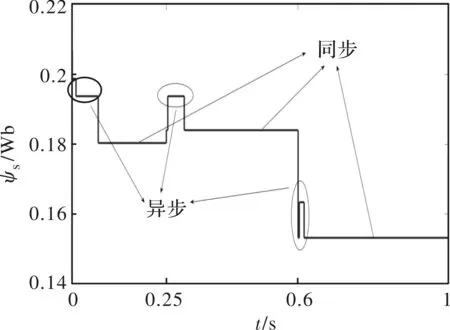
图8 搜索磁链曲线

图8搜索的磁链响应曲线表明，在起动、负载增加、加速时电机处于转子异步状态。由式(2)可得，本文在此时转子异步状态下考虑异步转子损耗电流，使搜索磁链在异步时增加，提高此时转矩动态响应速度，在同步时恢复到传统磁链搜索策略。电机额定磁链为2.168 Wb，而采用以最小功率为目标函数在线搜索当前工况下的最优磁链，可避免搜索过程中电机的抖动现象，其值均小于额定磁链。

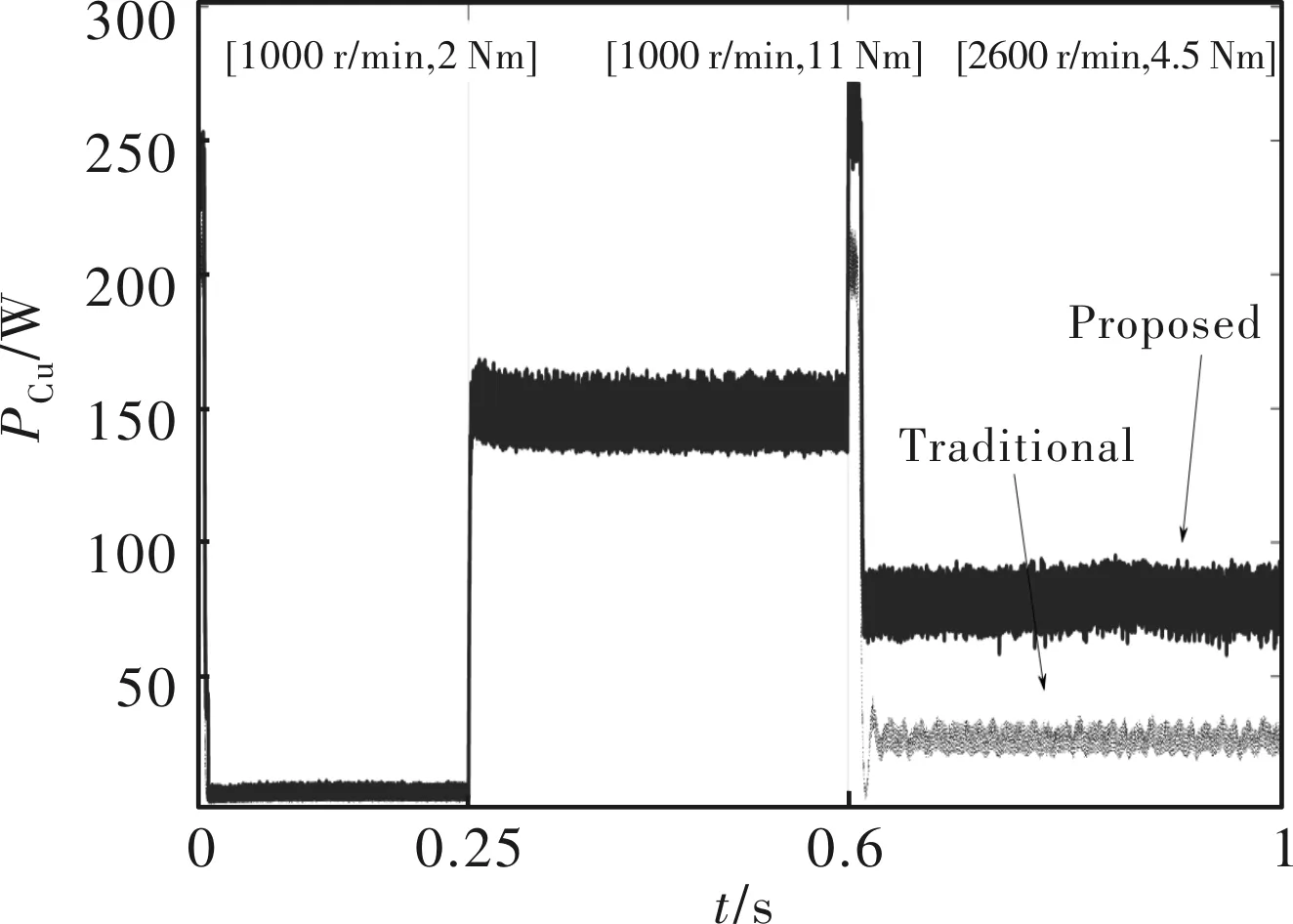
图9 铜耗曲线

图10 铁耗曲线

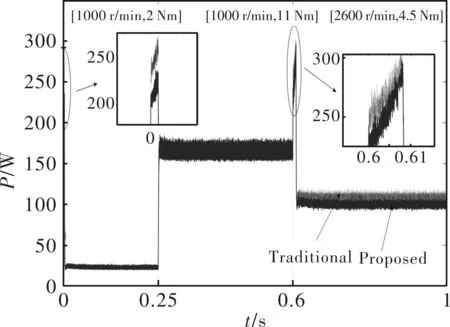
图11 总损耗曲线

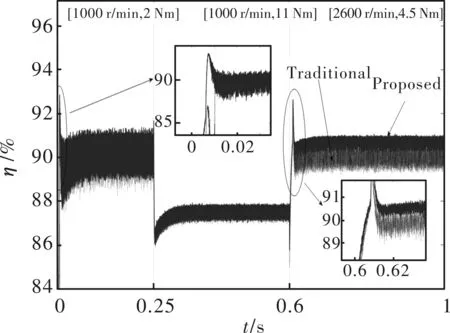
图12 效率曲线

图9至图12表明，在低速时，由于铁耗所占比例小，提出的控制策略效果不显著，效率提升大约为0.5%；在高速时，由1000 r/min到2600 r/min动态加速过程中，所提控制策略的铜耗最高比传统策略大50 W，铁耗小20 W，总损耗减少了37 W，即效率提升了大约1.8%；在低速负载变化时，所提策略降低了大约2 W的铁耗，而铜耗变化不显著，总损耗降低了26 W，对应的效率提高了1.3%；相比传统弱磁加MTPA，所提策略效率有利于节省电能，提高永磁同步电机工作效率。

5 结 论

本文首先简述永磁同步电机最小损耗控制策略的现状，分析永磁同步电机损耗模型的基础上，给出了考虑转子异步损耗的PMSM损耗最小控制。该控制方法同时考虑电机的铜耗和铁耗，并加入了转子异步损耗，基于黄金分割在当前工况下搜索最优磁链，并计算出最优d轴电流。该方法在保持搜索控制快速响应优点的同时，电机的总损耗明显减少了，电机效率提高了，达到了节能环保，因此具有良好的实用价值和广阔的应用前景。