考虑磁饱和效应的永磁同步电机高精度数学模型分析

卓 亮，王 波，刘成思，徐永向

(1.贵州航天林泉电机有限公司，贵阳 550000；2.陆装驻贵阳地区军事代表室，贵阳 550000；3. 哈尔滨工业大学，哈尔滨 150000)

0 引 言

永磁同步电机具有结构简单、功率密度高、损耗低、运行稳定等优点，在国防科技、家用电器、工农业生产等领域得到了广泛的应用[1-2]。然而，由于磁饱和引起的电感变化，导致电机的输出转矩和电流之间呈现非线性关系，导致传统的永磁同步电机线性数学模型无法计算出精确的结果，从而无法实现高精度的电机控制。为了获得更高的精度，可以采用场路耦合模拟的方法，但是这种方法每一步都需要进行一次电磁场有限元计算，导致计算速度极低，效率低下[3]。为了能够准确且快速地进行电机的性能分析，建立能够考虑磁饱和影响的数学模型是十分必要的。

国内外众多学者针进行了相关研究，提出了几种研究方法来描述磁饱和对电机的影响。这些方法主要是使用修正系数来进行电感和磁通的修正[4-6]，然而这些方法都不能很好的满足精度要求。

本文提出了一种新型永磁同步电机数学模型。首先通过若干个工况的有限元计算，获取电感、电流以及转矩的计算结果，构建电感与电流、转矩与电流之间的对应关系，在此基础上使用插值方法，将上述对应关系由特定工况扩展至全工况。通过插值得到的模型其原始数据来自于电磁场有限元计算，所以其计算精度可以达到有限元计算级别。同时，在完成模型的建立后，不再需要进行有限元计算，只需根据工况在模型内进行插值计算即可，保证了模型的计算速度。

1 传统的永磁同步电机数学模型

传统的永磁同步电机数学模型基于交直轴电压方程以及转矩方程进行建立，其表达式如式1所示：

(1)

式中,Vd为直轴电压，Ld为直轴电感，id为直轴电流，Vq为交轴电压，Lq为交轴电感，iq为交轴电流，Tem为电磁转矩，Rs为电阻，ωe为电机转速，ψm为永磁体磁链，m为电机相数。

在传统的永磁同步电机数学模型中，Ld与Lq被视作常数，因此电磁转矩Tem随电流id与iq呈现线性变化。传统的永磁同步电机线性数学模型计算简单且迅速，但是其一方面忽略了磁饱和效应所造成的的非线性影响，另一方面没有考虑到转子位置改变所造成的影响，导致模型的精确度欠佳。因此，建立能够考虑磁饱和效应以及转子位置影响的永磁同步电机数学模型是十分必要的。

2 新型计算模型

为了解决传统的永磁同步电机线性数学模型存在的问题，提出了一种新的计算模型。在该计算模型中，Ld与Lq不再是常数，而是与电流id、iq和转子位置θ相关的函数，具体的函数关系将在后文中由若干工况的有限元计算结合插值等数学方法获得。所提出的模型表达式如式为

(2)

此外，由于式(2)中的转矩方程只考虑了电流作用而产生的转矩，而没有考虑齿槽转矩等影响，所以对转矩方程也进行修正，也将其表示为与电流id、iq和转子位置θ相关的函数，如：

Tem=h(id,iq,θ)

(3)

交直轴磁链Ld、Lq以及转矩Tem与电流和位置的具体函数关系将在后续由若干个工况的有限元计算配合插值方法来进行求解。使用上述函数关系进行模型的建立，可以充分考虑磁饱和效应以及转子位置所带来的影响。

所提出的新型计算模型的示意图如图1所示。

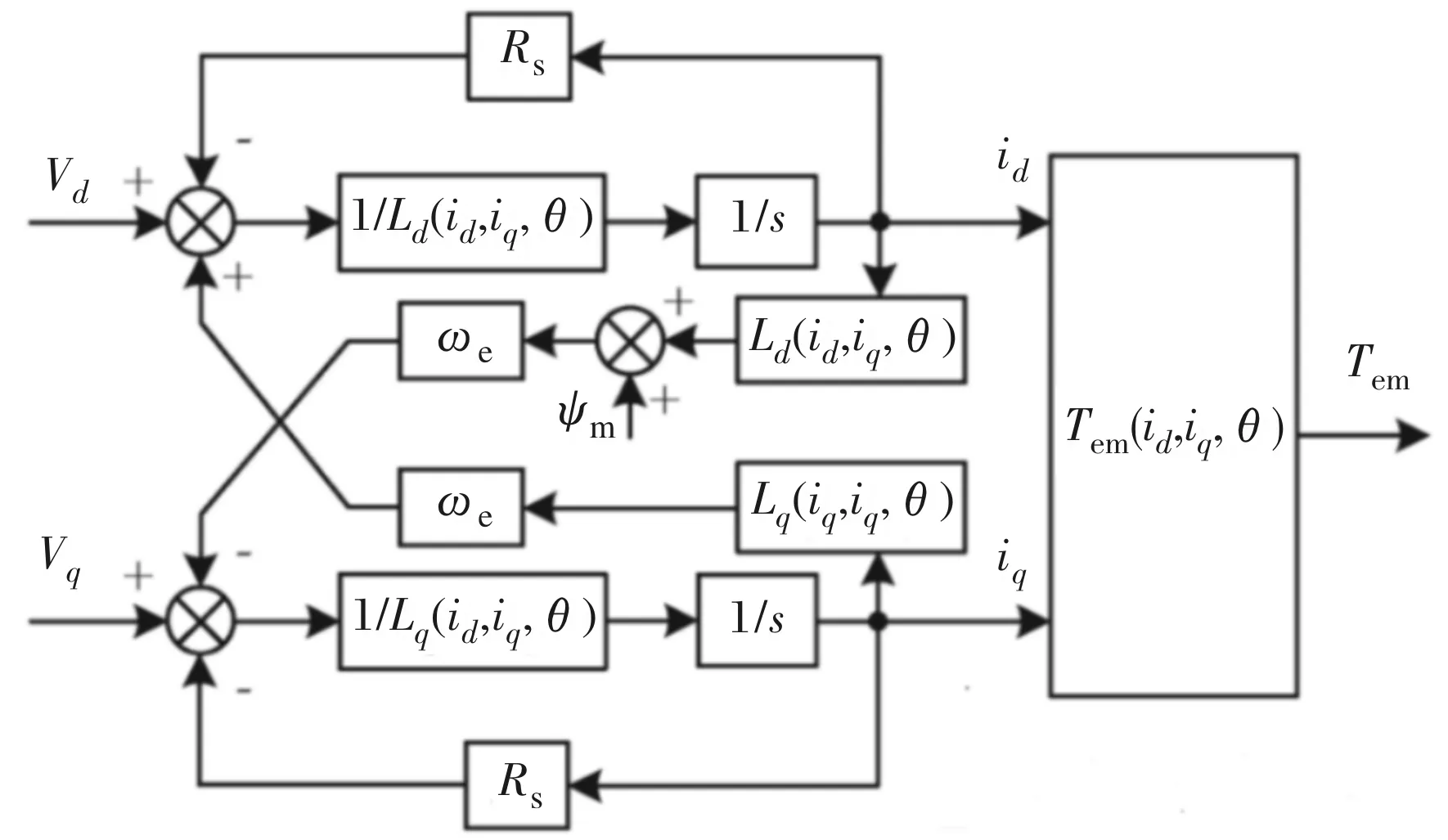
图1 新型计算模型的结构

由图1可知，当电机处于特定工况下，即给定电压Vd和Vq时，首先可以通过模型进行电流id和iq的计算。然后一方面可以通过函数关系Ld(id,iq,θ)和Lq(id,iq,θ)进行交直轴电感Ld和Lq的计算，从而完成下一次的计算步骤，另一方面通过函数关系T(id,iq,θ)进行转矩的计算。更进一步，可以使用转矩Tem结合电机运动方程进行转子位置θ的计算。

由于上述函数关系，即Ld(id,iq,θ)、Lq(id,iq,θ)以及T(id,iq,θ)是通过有限元计算结合插值方法得到的，所以有限元计算所考虑到的磁饱和效应的影响以及转子位置的影响在该模型中也得以考虑。所以该模型不同于传统的线性模型，是一种充分考虑非线性的数学模型，能够提供精确的电机性能计算结果，从而可以为永磁同步电机的高精度控制策略提供指导。

3 新型计算模型的建立

以一台10极12槽内置式永磁同步电机为研究对象，进行新型计算模型的建立，并在此基础上对其计算速度及计算精度进行验证。所使用的10极12槽内置式永磁同步电机结构如图2所示。

图2 10极12槽电机结构示意图

电机的相关参数如表1所示。

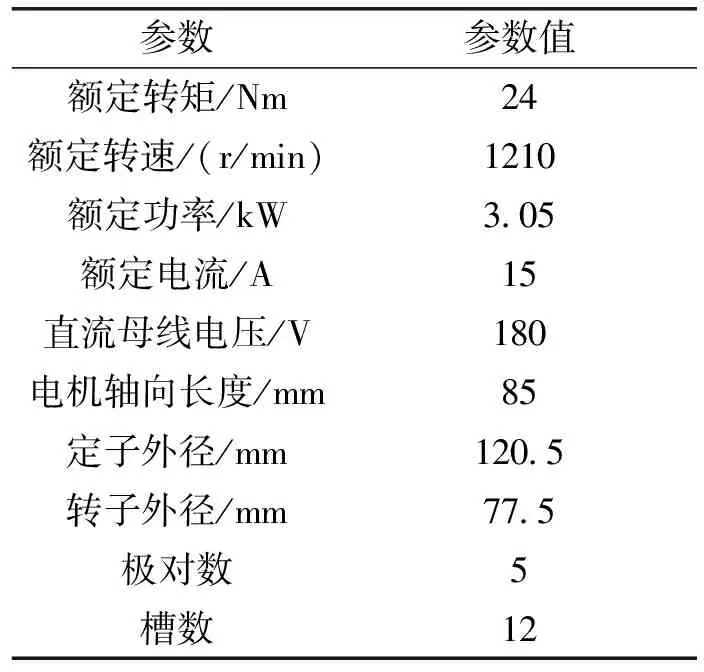
表1 电机参数

函数Ld(id，iq，θ)、Lq(id，iq，θ)和T(id，iq，θ)通过有限元计算得到。为了保证计算的精度，id和iq的范围应覆盖电机正常工作的电流范围。因此，id和iq的范围选择应该大于2倍过载电流，电流范围设置在-40 A和40 A之间，电流的变化步长为10 A，因此有限元计算中id和iq的样本数均为9，即进行了81个工况的有限元计算。转子位置θ在电角度0°到360°范围内变化。为了准确地描述转矩和电感的变化，设置有限元分析中θ的步长为3°，样本数量为121。综上所述，通过有限元计算可以得到81个工况的计算结果，每个计算结果内包含121个数据点，共计9801个数据结果。

基于这9801个有限元计算的数据，采用插值法建立模型。完成插值后，可以获得直轴电感Ld、交轴电感Lq以及转矩Tem随直轴电流id、交轴电流iq以及转子位置θ变化的三维矩阵。上述三维矩阵即可进行关系Ld(id，iq，θ)、Lq(id，iq，θ)和T(id，iq，θ)的描述。当给定id、iq以及θ时，即可在三维矩阵中通过插值以类似查表的方法进行直轴电感Ld、交轴电感Lq以及转矩Tem的计算。

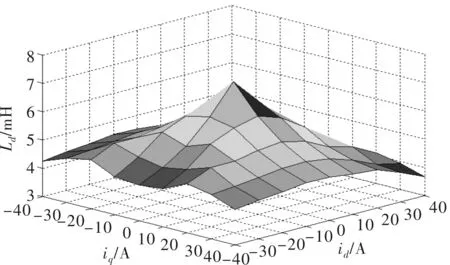
图3 电角度0°时直轴电感随电流的变化

为了直观地进行表示，将转子位置固定在特定的角度0°，此时可以将上述三维矩阵简化为二维矩阵。d轴电感和q轴电感在转子位置为0°时与id和iq的关系呈现出二维曲面的形式，如图3和图4，可见，电感随着id和iq而变化，这意味着电流导致的磁饱和效应会影响电感的数值，并非如传统线性模型所认为的电感为常数。新型计算模型将这一特性考虑在内，所以能够获取更加精确的电机性能计算结果。

同理，可以获取转矩在转子位置为0°时与id和iq的关系，所呈现的二维曲面如图5所示。

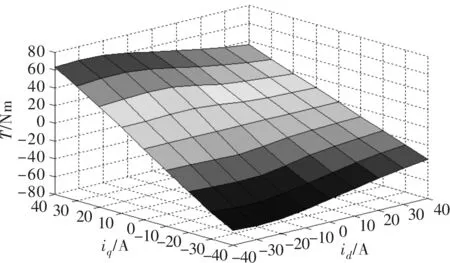
图5 电角度0°时转矩随电流的变化

需要注意的是，虽然只进行了特定电流和转子位置的81个工况，9801个数据点的有限元计算，但是基于上述数据构建模型后，使用三维插值可以将进行任意电流和转子位置角所对应的电机性能的相关计算。

使用传统线性模型以及本模型分别进行电机转矩特性的计算，所得到的结果如图6和图7所示。

图6 不同模型计算的转矩特性

图7 不同模型计算的转矩波形

由图6可知，所提出的新型计算模型计算出的转矩随iq呈现非线性变化，证明本模型考虑了磁饱和效应所导致的非线性影响。由图7可知，所提出的新型计算模型计算出的转矩随转子位置呈现波动，证明本模型考虑了转子位置的影响。

4 模型的验证

使用建立完成的计算模型进行永磁同步电机额定运行状态的性能计算。电机额定状态为id=0 A，iq=15 A，输出转矩24 Nm。根据该工况给定特定的电压输入，则由于转子位置的影响，id与iq呈现六次波动，如图8和图9所示。分别使用新型计算模型以及给定电压输入的有限元进行电机额定状态输出转矩的计算，计算结果如图10所示。由图10可知，由于新型模型的基础数据来自于有限元计算的81个工况的计算结果，所说义新型计算模型的转矩计算结果与场路耦合法计算得到的结果十分吻合，但是其计算速度远快于有限元计算，因此新型计算模型的准确性与快速性均得到了验证。

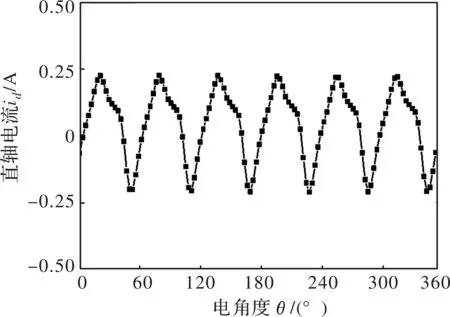
图8 直轴电流波形

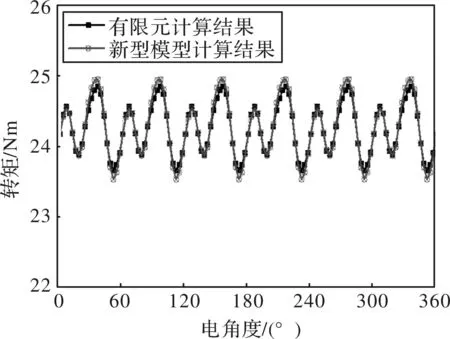
图10 不同方法的转矩计算结果

5 结 论

本文提出一种新型永磁同步电机数学模型。通过若干个工况的有限元计算，获取电感、电流以及转矩的计算结果，构建电感与电流、转矩与电流之间的对应关系，在此基础上使用插值方法，将上述对应关系由特定工况扩展至全工况。通过插值得到的模型其原始数据来自于电磁场有限元计算，所以其计算精度可以达到有限元计算级别。在计算时，通过已有数据进行插值计算即可获取当前工况的电机性能，不再需要有限元计算，因此计算速度得到了保证。本计算方法能够实现电机性能的快速高精度计算，能够为高品质的电机控制策略提供保证。