城市生鲜食品冷链物流配送路径优化技术研究
明小菊,珠 兰
(1.太原学院,太原 030032;2.西安邮电大学,西安 710061)
0 引言
人民生活水平的提高,促进了生鲜食品物流的持续增长[1]。生鲜食品易腐,需要进行冷链运输,除增加配送成本外,配送时效也影响其质量,进而影响消费者的购物体验[2]。通过合理优化冷链物流车辆的路径,可以降低配送车辆的碳排放,保证生鲜食品的质量,提高客户的满意度。因此,研究生鲜食品冷链物流配送路径的优化方法具有重要的现实意义。
对于生鲜食品物流配送路径优化问题,国内外学者进行了大量的研究,并取得了一些优异的成果。方文婷等[3]提出以最小化总成本构建冷链配送模型,并通过改进蚁群算法进行求解,通过仿真对该方法的优越性进行验证。张倩等[4]提出一种考虑了配送成本、生鲜新鲜度、碳排放量和客户需求不确定性的多目标配送模型,并通过改进的果蝇算法进行求解,该方法具有很高的鲁棒性,可以有效降低需求不确定性造成的干扰。张瑾等[5]提出一种以最小化总成本和最高客户满意度构建配送模型,将改进的蚁群算法用于模型求解,该模型可以满足实际需求,改进后算法的收敛速度和分辨率结果均优于改进前。宁涛等[6]提出以最小化总成本和最小化碳排放量建立配送模型,将改进的量子蚁群算法用于模型求解,该方法能够实现冷链物流配送路径优化,同时减少碳排放量和配送成本。但是,上述研究在成本构成上还不够充分,大多数研究都考虑了固定运输成本和时间窗,但在目标模型中没有具体的体现,存在一定局限性,需要改进和完善。
本文在满足需求点时间窗和需求量的前提下,以最小化总成本为目标构建冷链配送优化模型,并采用莱维飞行(Levy Flight,LF)和反向学习(Reverse Learning,RL)优化的粒子群算法(Particle Swarm Optimization,PSO)对模型进行求解。通过试验对方法的优越性进行验证,以期为冷链物流配送优化方法的发展提供参考。
1 冷链配送模型的建立
1.1 目标函数
配送总成本主要由固定成本、运输成本、冷藏成本、货运损坏成本和超限惩罚成本组成。
(1)固定成本
安排车辆以满足配送需求所产生的固定成本,如车辆维修、保养、折旧和人员工资。记录为C1,如下式所示[7]。
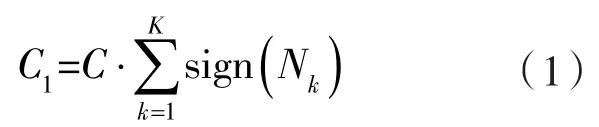
式中 C ——一个配送任务的固定成本;
Nk——配送过程所需的需求点数;
sign(Nk)—— 车辆k是否处于使用状态,使用就产生成本;
K ——参与配送车辆数。
(2)运输成本
运输成本即燃油成本,配送线路越短燃油成本越低,与距离成正比。运输成本被表示为正相关函数,记录为C2,如下式所示。

式中λ0——单位距离运输成本;
dij——需求点i到需求点j的距离;
xijk—— 车辆k是否是从需求点i到j,如果是,则为1,否则为0;
n ——配送点数。
(3)冷藏成本
在配送中需要维持一定温度,冷链设备的能耗记录为C3,如式(3)所示。
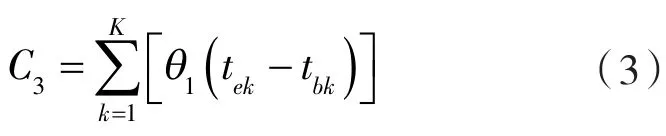
式中 θ1—— 车辆配送过程中用于维持单位时间内车辆温度的能量损失;
tek——第k辆车返回配送中心的时间;
tbk——第k辆车从配送中心出发的时间。
(4)货物损坏成本
生鲜食物容易腐烂变质,主要包括运输和卸载中货物损坏的成本,记为C4。运输过程中车厢温度恒定,但在卸载期间车厢温度因热交换而升高,因此在运输和卸载期间货物的损坏率不同,计算如下式所示[8]。

式中 ri——离开客户i时车内重量;
v ——配送车行驶速度;
λ3,λ4—— 运输和卸货过程中单位时间内货物损坏率;
tj——客户j卸货需要的时间;
p ——运输途中的单位货损成本。
(5)超限惩罚成本
[tei,tij]为时间窗,由最早 tei和最晚 tli服务时间组成。在指定的时间范围内交货可以节省企业的成本,并有利于统一处理和卸载货物。由于配送车辆和人力资源有限,到货时间可能会延迟或提前,从而增加配送成本。
采用软时间窗口作为约束,如果在该时间段内达到需求点,则没有罚款成本;否则,将产生罚款。如果早于需求点到达,则需要支付一定的等待成本;如果迟于需求点到达,将产生延误罚款。软时间窗惩罚函数分为3部分,如下式所示。

式中 α,β —— 单位时间的早到等待和迟到惩罚成本。
以最小化总成本为目标构建冷链配送优化模型,如下式所示。

1.2 约束条件
确保每个配送点只有1辆车用于配送服务,如式(7)和(8)所示[9]。
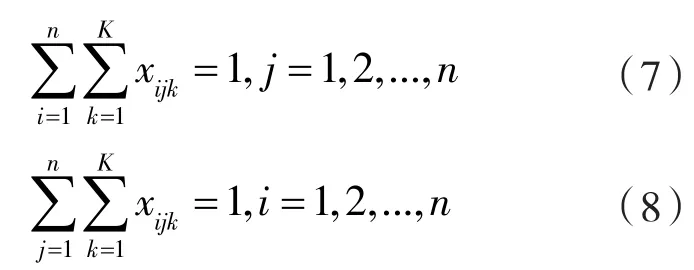
保证每辆车的负荷量不超过其自身最大负荷,如下式所示。

式中 qj——第j个客户的需求。
确保每辆车的轨迹路线是一个闭环,如下式所示[10]。
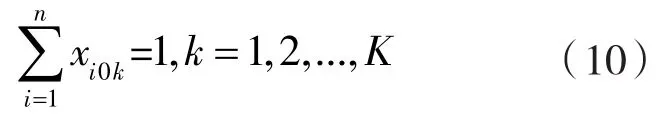
保证满足配送点时间窗要求,如下式所示。
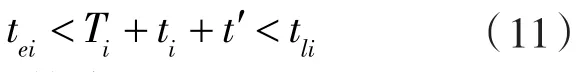
式中 ti——配送点等待时间;
t'——卸载时间。
2 改进粒子群算法求解
粒子群算法有很多优点,如精度高、适应性强等。但是,首领粒子的主动搜索能力非常弱,对于粒子的局部和全局搜索非常不利,对解的精度影响很大[11]。针对该问题,本文提出一种采用莱维飞行和反向学习优化的粒子群算法。
2.1 粒子群算法
粒子群优化算法基本思想是使用“粒子”作为进化过程中优化问题的解,其中适应度决定了粒子的优越性,每个粒子的适应度则由目标函数决定[12]。在一维目标搜索空间中,粒子数为N,对粒子的状态进行更新,如式(12)和(13)所示。
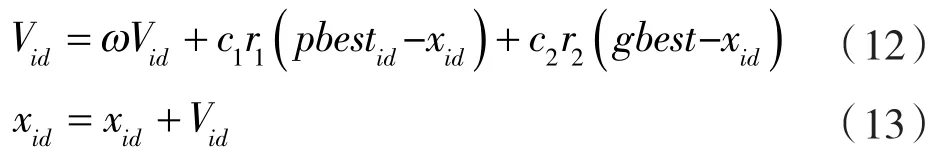
式中 c1,c2——自学习和社会学习因子;
xid,Vid—— 第 i个粒子在 d 维中的位置和速度;
ω —— 惯性权重,值越大,粒子的搜索能力越强;
r1,r2——随机数。
2.2 改进粒子群算法
为避免粒子群算法陷入局部最优导致算法搜索停滞,通过反向学习进行优化。在陷入局部最优搜索停滞时,向粒子个体最差位置进行学习,提高种群多样性的同时,提高算法的搜索能力,通过判断更新情况看是否处于停滞。在停滞时引入反向学习机制,第i个粒子在个体历史最差位置表示为 W1=(wi1,wi1,…,wij,wiD),则反向学习中粒子的速度更新如下式所示[13]。

式中 c3——反向学习的学习因子;
wiD——第i个粒子在d维空间中的位置。
莱维分布是在20世纪30年代由法国数学家莱维提出[14]。已有文献表明,在自然界中,莱维飞行模式与很多昆虫和鸟类的觅食轨迹相符合。
通过莱维飞行优化的粒子群算法可以有效地防止局部优化。由于莱维分布的复杂性,通常采用Mantegna算法对其进行仿真,步长计算如下式所示。

式中 β ——莱维分布的参数,取值1.5;
最后,粒子步长如下式所示。

式中 α—— 步长调整因子,根据具体问题进行调整,并将其保持在适当的范围内,
以使飞行步长不会太大或太小。
通过莱维飞行获得反向学习的步长,改进粒子群算法的速度更新,如下式所示[15]。
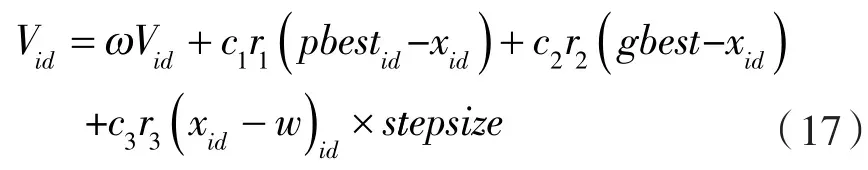
综上所述,改进粒子群算法的步骤如下:
(1)对种群进行初始化。
(2)对粒子的初始适应度进行计算。
(3)找到种群进化过程的个体和全局最优。
(4)将个体最优未更新次数与设定值进行比较。大于设定值采用式(17)和(13)进行粒子位置更新。否则,采用式(12)和(13)。
(5)判断结束条件是否满足,不满足返回第2步,满足则继续执行,输出最优解。
3 试验结果与分析
3.1 试验参数
试验设备为联想PC机,操作系统为Windows 7 64位旗舰版,Intel i5 2450m CPU,2.5GHz频率,8 GB内存,采用MATLAB R2018A作为仿真平台。改进的粒子群优化算法的参数:学习因子c1=c2=1.494 45,c3=1.4,反向学习阈值10,惯性权重ω=0.55,莱维飞行参数α =0.01,β=1.5。
考虑单个固定生鲜食品冷链仓库,经度为126.143 962°,纬度为 45.626 479°。针对时间和车辆载重等的限制,规划1个最优配送方案,将生鲜食品有效地分配到所有零售点,尽量降低配送总成本。各配送点的位置和需求信息,如表1所示。
为方便距离数据采集,将配送站编号为0。模型参数设置见表2。
3.2 试验分析
为验证文中方法的优越性,将文献[16]中的HPSO算法的优化结果与改进算法进行比较,分析算法的优缺点,通过MATLAB进行编程。根据目标函数,计算最小化总成本的最优配送方案。在具体的试验过程中,取30次运行的平均值和标准差,对其结果进行分析,结果见表3。

表3 算法对比Tab.3 Algorithm comparison
由表3可知,改进算法获得的平均路径成本低于HPSO算法的均值,标准差也较小。
表4所示改进算法在30次求解中的最优结果,包括配送路线、车辆装载件数、装载率、准时率和总成本等。

表4 求解最优结果Tab.4 Solution of the optimal result
为验证改进方法规划配送路径的实际意义,将原配送方案与改进方案进行对比分析。原始配送计划如表5所示。

表5 原始配送方案Tab.5 Original distribution scheme
比较表4和表5可以看出,改进算法求解30次的平均成本低于原配送成本,且准时率达到100%。配送总成本由2 502.20元降低到1 823.23元,降低了678.97元。因此,改进算法能够找到更加合理的配送方案,具有一定的现实意义。
4 结语
本文在考虑需求点时间窗和需求量的前提下,以最小化总成本为目标构建冷链配送优化模型,并通过莱维飞行和反向学习对粒子群算法进行优化用于模型求解。通过试验验证方法的优越性。结果表明,路径优化方法可以为生鲜食品的冷链配送找到最优路径,与改进前相比有了明显的改进,不仅配送成本降低了678.97元,而且准时率提高到100%。考虑到目前的试验设备和数据规模,本文研究的配送路径优化方法仍处于准备阶段。后续研究将在此基础上进一步完善冷链物流配送方法,以适应未来不断变化的应用环境。

