废弃纤维素纤维制备的多孔炭吸附 动力学及其体系设计

孙宝芬　蒲泽鹏　陈国强　李晓晨

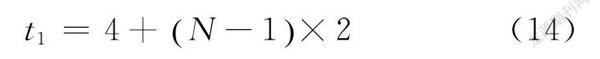
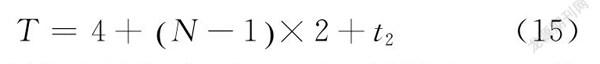
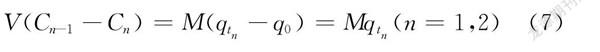
摘要：为了探究纤维素纤维制备的多孔炭材料去除水中有机染料的吸附性能并设计合理的吸附体系，以废弃再生纤维素纤维制备的多孔炭为吸附剂，甲基橙染料为吸附质，构建了不同的吸附体系，获得吸附平衡和动力学数据。运用Langmuir和Freundlich吸附等温方程评估材料的吸附平衡，应用准一级和准二级动力学模型对动力学数据进行了模拟，进而基于平衡和动力学模拟结果，采用静态吸附法评估了吸附体系所用的吸附剂用量和最优吸附时间。结果表明：Freundlich吸附等温线方程更适合于评估该多孔炭材料吸附甲基橙的吸附平衡，说明表面吸附不均匀且存在多层吸附;准二级动力学模型能很好地描述该多孔炭吸附甲基橙的所有吸附过程;两级吸附器模型可以在短时间内实现较高的甲基橙去除效率。

关键词：多孔炭;吸附;甲基橙; 动力学;吸附设计

中图分类号：TS159; X791文献标志码：A文章编号：1009265X（2022）03016608

Kinetics study and system design of adsorption on porous carbon prepared

from waste cellulose fiber

SUN Baofen PU Zepeng CHEN Guoqian  LI Xiaochen

Abstract： In order to explore the adsorption performance of the porous carbon material prepared from waste cellulose fiber on removing organic dyes from water and to design a reasonable system， different adsorption systems， in which the porous carbon prepared using waste regenerated cellulose fiber was used as the adsorbent and methyl orange dye was used as the adsorbate， were established. Adsorption equilibrium and kinetic data were obtained. The adsorption equilibrium of the material was evaluated using Langmuir and Freundlich isotherm formula. The experimental kinetic data were simulated using pseudofirst order and pseudosecond order kinetic models. Based on the results of equilibrium and kinetic simulations， the adsorbent dosage and the optimal adsorption time were evaluated by the batch adsorption method. Experimental results show that the Freundlich adsorption isotherm formula is more suitable to evaluate the adsorption equilibrium of the porous carbon for methyl orange， indicating that the adsorbent surface is heterogeneous and a multilayer adsorption occurs on the adsorption surface. The pseudoorder kinetic model can describe all the adsorption process of the carbon for methyl orange， and the twostages batch adsorber model can achieve high removal efficiency of methyl orange in a shorter time.

Key words： porous carbon; adsorption; methyl orange; kinetics; adsorption design

紡织印染加工是纺织生产产业链中重要的一环。在印染加工过程中，大约20%的染料无法固着于织物上而分散在水中[1]，印染废水虽然经过一定的处理，但仍有大量染料被释放到水生态系统中。纺织用染料多数为有机合成染料，这些染料不仅会破坏水生态系统，而且具有毒性、易致癌和致突变的特性，严重威胁着人类健康。为了缓解染料污水对环境和人类的危害，科研工作者已经在开发无水染色技术[2]，但该技术还没有得到广泛的应用和推广。在开发环保染色技术同时，传统染色方式在生产中仍占据绝对的优势，因此，印染废水的处理仍是现代工业废水治理中的重点。多孔炭材料具有丰富的孔隙和非常高的比表面积，其化学性质稳定，是非常通用的吸附剂材料，被广泛应用于废水处理工业中。

吸附是一种物质进入另一种物质中直到形成一个均匀相，并逐渐达到吸附平衡的过程。在整个过程中同时存在吸附和脱附两种运动，所谓的吸附平衡是一种动态平衡。平衡时吸附量大小反映了吸附材料的吸附能力。在不同吸附体系中，多孔炭材料表现出不同的吸附动态变化过程和不同的吸附能力。一个设计良好的吸附体系是实现吸附性能最优化的前提，反过来，吸附体系的吸附动力学和吸附平衡实验参数是吸附体系设计的理论基础。本课题组利用废弃的纤维素纤维制备了一种性能优异的多孔炭材料，为了探究该多孔炭材料在应用中的最优吸附体系，深入分析了该材料吸附甲基橙染料的动力学，探究该材料吸附过程适宜的动力学模型。在固液吸附体系中，常用的吸附动力学模型有准一级（Pseudofirst order， PFO）动力学和准二级（Pseudo second order， PSO）动力学模型[34]。通过动力学模型适应性分析，可以获得影响吸附速率的限制性步骤和吸附机理，进而为吸附体系的设计提供理论依据。

当前有机染料的吸附研究大多集中在吸附能力评估、吸附动力学和热力学研究，而对吸附体系设计研究的相对少。在这些少数的研究中，常用的吸附体系有静态吸附[5]和固定床吸附[6]。固定床吸附法是吸附剂被固定在吸附器中，一定浓度的染料污水通过吸附器时，利用高浓度差压力驱使吸附剂吸附污染物。静态吸附是定量的吸附剂和污染物溶液，通过调整吸附剂和吸附质的接触时间来达到去除污染物的吸附过程，该方法易于操作、成本低。

本文以前期制备的废弃再生纤维素纤维为原料制备的多孔炭为吸附剂[7]，以甲基橙染料作为吸附质，首先确定该多孔炭材料的吸附动力学和吸附平衡，并在此基础上，利用静态单级吸附和两级吸附模型对吸附剂用量和最优吸附时间进行了评估，优化吸附工艺，保证吸附效率的前提下优化吸附时间，研究结果可为该多孔炭吸附剂材料的应用提供理论依据。

1实验

1.1试剂与仪器

材料：甲基橙染料（摩尔质量为327.3 g/mol），氢氧化钠，氯化氢溶液（质量浓度为37%），均购自国药集团化学试剂有限公司;多孔炭材料，根据文献[7]自制，因含有分级孔，标记为HPC。

儀器：BSA124SCW型电子分析天平（赛多利斯科学仪器有限公司）;S232型恒温磁力搅拌器（上海司乐仪器有限公司）;PHS3E型pH计（上海仪电科学仪器股份有限公司）;TGL16G型高速离心机（上海安亭科学仪器厂）;TU1901型紫外可见光光度仪（北京普析通用仪器有限公司）;移液枪（赛默飞世尔科技（中国）有限公司）。

1.2吸附试验

首先称取0.1 g甲基橙粉末配成1000 mg/L的染料溶液作为母液，然后根据实际实验要求稀释成不同质量浓度的测试液。甲基橙溶液浓度可根据紫外可见光光度仪测试的吸光度值计算而得，而甲基橙吸光度值与质量浓度之间的关系可根据甲基橙质量浓度标线获得。所有的实验在没有特别说明的情况下，都进行了2次平行实验，实验结果为测试平均值。

1.2.1吸附剂用量对吸附性能的影响

分别称取2.5、5.0、7.5、10.0 mg和20.0 mg的HPC吸附剂材料分散到25.0 mL质量浓度为100 mg/L的甲基橙溶液中，磁力搅拌24 h使吸附体系达到平衡，离心分离固体吸附剂和溶液，使用紫外可见光光度仪测定溶液的质量浓度，根据式（1）计算不同固液比吸附体系的吸附量。

式中：Ct和C0分别是吸附t min和吸附初始时的溶液质量浓度，mg/L;qt表示吸附一定时间的吸附量，mg/g，当达到平衡时，其结果为平衡吸附量;V是溶液的体积，L;m代表吸附剂的投入质量，g。

1.2.2吸附平衡等温线测试

称取10.0 mg的HPC材料分散到25.0 mL不同初始质量浓度的甲基橙溶液中（20～300 mg/L），磁力搅拌24 h，HPC材料达到吸附平衡，离心分离固体吸附剂和溶液，量取一定量的上清液并稀释到测试浓度，使用紫外可见光光度仪测定溶液的质量浓度，根据式（1）计算材料吸附平衡时的吸附量。以不同初始质量浓度的吸附量为纵坐标，吸附后溶液平衡质量浓度为横坐标，绘制多孔炭材料的吸附平衡等温线。

1.2.3吸附动力学测试

甲基橙溶液初始质量浓度分别为56、100、200、300 mg/L，试验温度为20 ℃。将40.0 mg的HPC分散于100.0 mL不同初始质量浓度的甲基橙溶液中，在磁力搅拌条件下，按照一定的时间间隔从吸附体系中量取0.5 mL的液体并快速稀释一定倍数，离心去除液体中的固体，然后利用紫外可见光光谱仪测试溶液的吸光度值，从而计算获得吸附后剩余溶液的甲基橙质量浓度。

2理论模型

2.1吸附平衡模型

多年来，许多吸附等温线模型已经被广泛研究与应用。其中，最常用的模型有郎格缪吸附等温线（Langmuir isotherm）和弗兰德里希吸附等温线（Freundlich isotherm）。Langmuir等温线的假设前提是吸附剂的表面吸附为均匀的单层吸附，即吸附剂表面所有位点对吸附质具有相同的亲和力[8]。一个吸附位点一旦被吸附质分子占据，就不再吸附其它分子。Langmuir模型的非线性表达式如式（2）所示：

式中：Ce是吸附平衡时溶液的质量浓度，mg/L;qe表示平衡时吸附剂的吸附量，mg/g;qm是Langmuir公式中与吸附材料的最大吸附能力相关的常数，mg/g;而KL是与吸附能有关的常数，L/mg。

Freundlich等温线模型假定吸附过程是通过多层吸附机制在异质表层进行[9]。等温线方程如式（3）所示：

式中：KF和n分别是对应于吸附能力和吸附强度的常数。

2.2动力学模型

染料于水溶液中在固体表面上的吸附遵循4个步骤[3]：a）在本体溶液中扩散;b）通过液/固界面膜的传质;c）孔扩散;d）在吸附剂上的吸附孔表面吸附。通常吸附过程的动力学分析可以给出吸附的基本性质和机理，本实验采用准一级动力学模型（PFO）和准二级动力学模型（PSO）两个动力学模型对多孔炭吸附甲基橙的动力学数据进行模拟分析。

2.2.1准一级动力学模型（PFO）

PFO动力学模型是预测有机分子在液相固体上吸附动力学最常用的模型公式之一。该模型方程的非线性形式如式（4）所示，其线性形式如式（5）所示[10]：

式中：k1表示吸附速率常数，min-1。通过对实验数据进行线性拟合，所得拟合直线的截距为lnqe，斜率为k1，据此可以获得理论平衡吸附量和吸附速率常数。

2.2.2准二级动力学模型（PSO）

PSO动力学模型是基于假设通过离子交换机制的吸附速率控制整个吸附动力学的基础上发展起来的，其方程的常用线性形式如式（6）所示[10]：

式中：k2表示PSO动力学模型的吸附速率常数，g/（mg·min）。通过t/qt与t的关系图，可以绘制一条拟合直线，其斜率为1/qe，截距为1/k2qe2，由此可计算qe和k2的值。

2.3静态吸附器设计模型

2.3.1单级吸附器模型

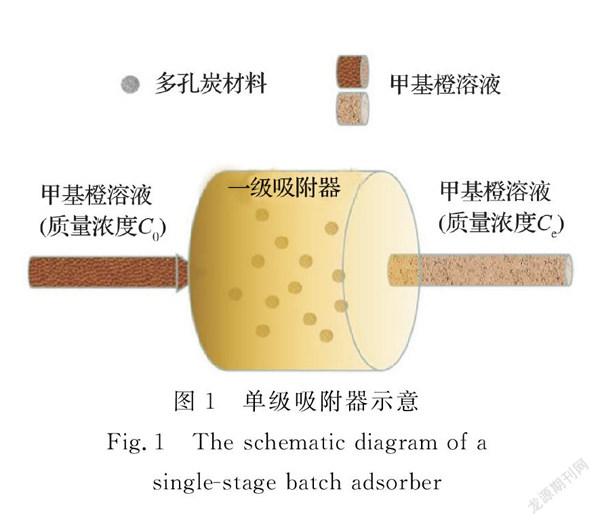
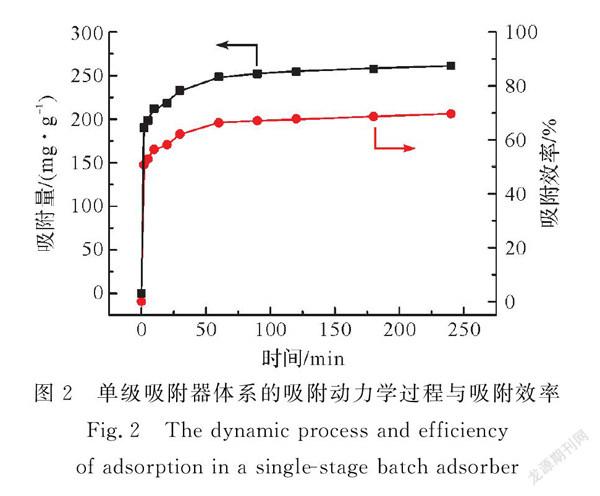
实验中的吸附体系是批量吸附实验，相当于单级吸附器，如图1所示。根据吸附体系中吸附平衡的研究，该模型可以评估吸附一定体积的染料溶液所需要的吸附剂用量[11]。但是，单级吸附体系是一个吸附直达平衡的过程，无法调控时间。图2是利用单级吸附体系多孔炭吸附甲基橙的动力学过程及其吸附效率图，从图2中可以看出，利用单级吸附体系，初始质量浓度为150 mg/L的甲基橙溶液达到平衡的时间超过60 min，且其最大吸附效率不到70%。根据吸附平衡和动力学数据的分析，单级吸附过程的吸附效能并不理想，达到吸附平衡所需要的接触时间相对较长，造成不合理的长吸附时间，从而会导致整个吸附处理过程的效率低下。

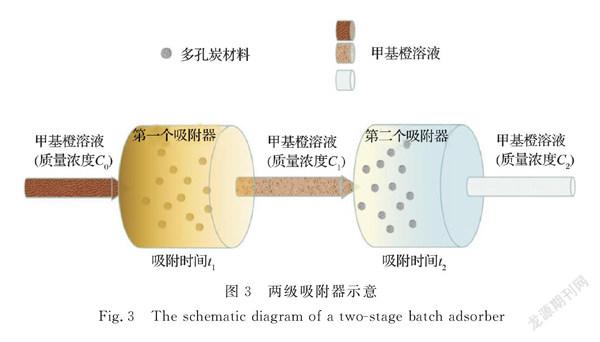
2.3.2两级吸附器模型

为了更好地平衡吸附效率和成本效率，两级吸附过程是最为常用的吸附方法[5]，如图3所示。吸附前设定体系目标吸附效率，一定体积、初始质量浓度为C0的甲基橙溶液经过第一个吸附器，该阶段的吸附时间为t1，然后，从第一个吸附器流出的甲基橙溶液再流入第二个吸附器，继续吸附时间t2，以达到设定吸附效率。通过调整两级吸附模型中不同吸附阶段的吸附时间，可以实现吸附时间的优化。

染料溶液经过第一个吸附器，经吸附时间t1后，其质量浓度从C0 减少到C1，吸附剂上吸附的染料吸附量从q0增加到qt1。接着，染料溶液流入第二个吸附器，经由同质量吸附剂吸附时间t2 后，溶液质量浓度从C1减小到C2，吸附剂的吸附量由q0增加到qt2。这样，染料废液依次通过两个负载一定质量吸附剂的吸附器，实现设定吸附效率的吸附模型称为两级吸附器模型。其中，吸附剂吸附甲基橙的初始吸附量q0均为0，根据质量守恒，在每个阶段都存在如式（7）的质量平衡：

3结果与讨论

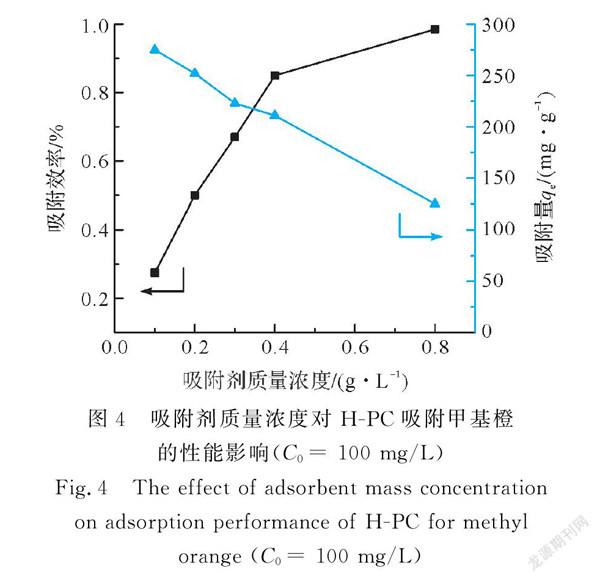
3.1吸附剂用量对吸附性能的影响图4描绘了吸附剂质量浓度对吸附效率和平衡吸附量的影响。从图4可以看出，随着吸附剂的质量浓度从0.1 g/L增加到0.8 g/L，单位质量吸附剂的吸附量呈线性下降趋势，而吸附体系的吸附效率不断增加，但是，当其质量浓度超过0.4 g/L，吸附效率增加速率明显变小。造成这些现象的原因是多方面的，吸附剂的增多增加了吸附体系中总的吸附比表面积和吸附位点，从而提高了吸附体系中甲基橙的总去除效率，然而，吸附剂的增加也影响悬浮液的物理特性，如增加溶液黏度，而阻碍了染料分子的扩散[12]。此外，在甲基橙初始质量浓度不变条件下，吸附剂用量的增加致使单位质量的吸附剂周围可吸附的染料分子数量减少，进而导致较低吸附驱动压力和吸附量。综合实验结果分析，0.4 g/L被选取为多孔炭材料HPC吸附性能研究的投入质量浓度。

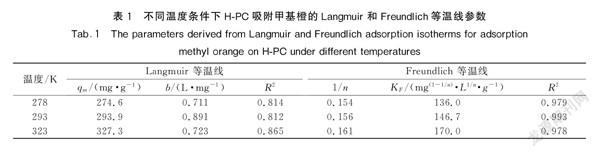
3.2吸附平衡表1列出了基于两种等温线模型导出的相应拟合参数值。从表1中可以看到，Freundlich等温线模型拟合的相关系数都大于0.97，其大于Langmuir等温线模型的相关系数，因此，Freundlich等温线模型能更好地描述吸附数据，说明该吸附剂表面吸附位点不均匀，吸附过程存在多层吸附机制，甲基橙分子间存在多层堆积现象。

3.3吸附动力学图5（a）和图5（b）分别是基于准一级动力学（PFO）和准二级动力学（PSO）模型对多孔炭吸附甲基橙動力学数据的拟合。从图5中可以看出，准一级动力学模型不能很好地预测实验数据，而准二级动力学模型能完美地与实验数据拟合在一起，动力学模型的相关系数也证明了准二级动力学的适合性（见表2）。表2列出了甲基橙动力学数据与准一级动力学和准二级动力学模型的线性拟合参数值。在甲基橙的不同初始质量浓度的体系中，PFO动力学模型的相关系数值都较小，而PSO动力学模型的相关系数（R22）都大于0.999，这表明，PSO动力学模型能更好地描述该多孔炭材料吸附甲基橙的动力学。此外，根据PSO动力学模型计算而得的吸附量（qe，cal）与用qe，exp表示的实验吸附量非常接近，而运用PFO动力学模型计算的吸附量与实际实验所得的吸附量差距很大。因此，与PFO动力学模型相比，PSO动力学模型更适合描述该多孔炭吸附甲基橙的动力学行为。

3.4吸附体系设计

3.4.1单级吸附器体系根据上面吸附平衡分析，该吸附材料的吸附平衡数据符合Freundlich平衡等温方程，因此，将Freundlich 方程（3）带入式（7），可以得到关系式（8）：

基于式（8），可以获得不同初始质量浓度时吸附剂质量与污染物去除效率的关系。表3所列的数量关系反映了初始质量浓度为200 mg/L的甲基橙溶液在不同温度条件下，吸附体系的体积与吸附剂用量的关系。

3.4.2两级吸附器体系根据前面甲基橙吸附动力学的分析，HPC吸附甲基橙的吸附动力学符合准二级动力学模型，因此将式（6）带入到式（7）中，获得每个吸附阶段染料溶液的质量浓度变化，如式（9）所示：

此外，甲基橙在每个吸附阶段的去除效率，

经二个吸附器吸附后，甲基橙的总去除率为R=R1+R2。将准二级动力学模型公式带入后，甲基橙总去除率可利用式（11）计算：

其中，每个吸附阶段中的qen和k2n可以用每个阶段的初始质量浓度Cn-1的幂函数表示[1314]，如式（12）和式（13）所示：

其中，Aq，Bq，Ak和Bk的值可以通过动力学研究中的qe和k2与初始质量浓度C0的关系进行幂函数拟合而获得，拟合参数值如表4所列。

为了优化吸附时间，设定第一个吸附阶段的吸附时间t1，从4 min开始，以2 min为时间间隔，不断增加到60 min。将每个设定的吸附时间段作为一个吸附体系，体系号记为N，这样，可以获得29个吸附体系，即N=1，2，3……，29。为了获得较高的染料去除效率（如80%、90%），染料溶液在第一阶段经吸附时间t1后，在进入第二个吸附器，继续经吸附时间t2，达到预期的去除效率，整个吸附过程所用的总时间为T=t1+t2。第一阶段吸附时间可以根据其吸附体系号计算获得，如式（14）所示：

所要求的總吸附时间为：

在设定预期去除效率后，t2可以根据式（11）计算而得。

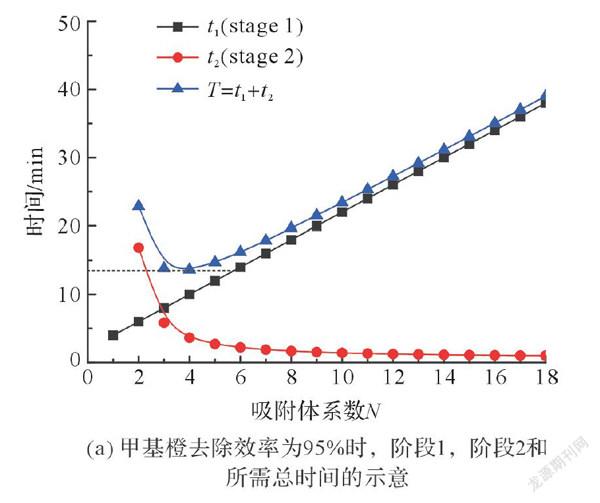
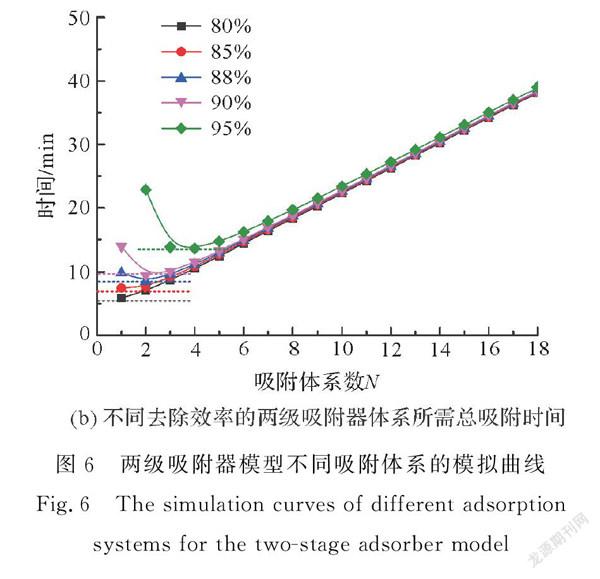
基于上述设计原理，本文模拟了甲基橙初始质量浓度为150 mg/L和200 mg/L的两级吸附体系。图6是1 L质量浓度为150 mg/L的甲基橙溶液经过含有0.4 g/L吸附剂的两级吸附器后，其去除效率达到一定值（80% ～ 95%）时，所需的吸附时间曲线图。其中，图6（a）描绘了去除效率为95%，阶段1吸附时间（stage 1）、阶段2吸附时间（stage 2）和总吸附时间，图6（b）描绘了不同去除效率的总吸附时间，从图6（b）可以得出体系的最优吸附时间设计。从图6（a）可以看出，150 mg/L甲基橙溶液的去除效率达到95%时，最短吸附时间发生在第4个体系，其中第一阶段的吸附时间为10 min，第二阶段所需吸附时间为3.63 min，总吸附时间是13.63 min。根据图6（b），利用两级吸附模型，150 mg/L甲基橙溶液经过4 min的吸附，其吸附效率即可高达80%，远高于单级吸附体系的吸附效率（见图2）。

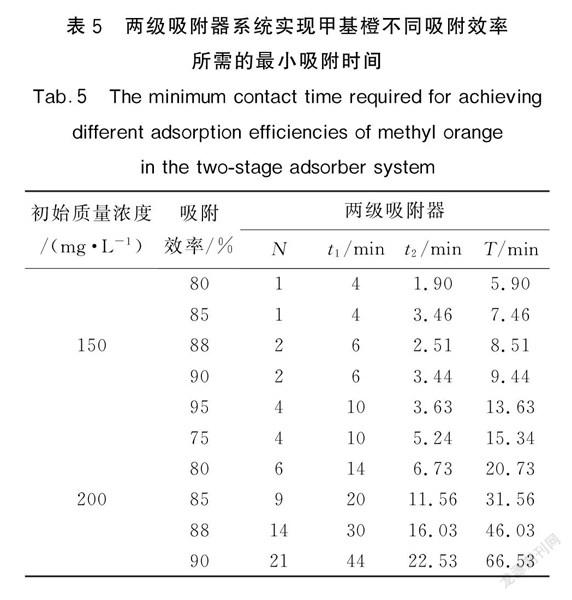
表5列出了利用两级吸附模型吸附150 mg/L和200 mg/L甲基橙溶液所需的吸附时间。甲基橙初始质量浓度为150 mg/L时，去除效率从80%增加到95%，所需最短吸附时间从5.9 min增加到13.63 min。初始质量浓度为200 mg/L时，吸附去除90%的甲基橙，需要的吸附时间至少为66.53 min，其中第一阶段吸附时间为44 min，第二阶段要求的吸附时间为22.53 min。

4结论本文利用自制的废弃纤维素纤维制备的多孔炭材料作为吸附剂，研究了其吸附甲基橙的吸附平衡和吸附动力学，并基于此，利用两级吸附器模型设计了该材料吸附甲基橙的吸附体系，对吸附时间进行了优化。通过研究分析得出：

a）吸附平衡数据的拟合结果揭示了吸附平衡等温线更加符合Freundlich模型，说明甲基橙在多孔炭中的吸附存在多层堆积吸附现象。

b）准二级动力学模型能完美地与吸附体系的实验数据相拟合。

c）基于准二级动力学模型的分析，两级吸附器模型可以在较短的吸附时间内实现较高的甲基橙去除效率，其吸附时间和吸附效率都优于单级吸附器模型。

参考文献：[1]SHARMA K， DALAI A K， VYAS R K. Removal of synthetic dyes from multicomponent industrial wastewaters[J]. Reviews in Chemical Engineering， 2017， 34（1）： 129.

[2]龙家杰，陈锋，魏晓晨，等.纺织品超临界CO2无水染色的产业化进程[J].染整技术，2015，37（8）：16.LONG Jiajie， CHEN Feng， WEI Xiaochen， et al. Industrialization process of textile supercritical CO2 anhydrous dyeing[J]. Textile Dyeing and Finishing Journal. 2015， 37（8）： 16.

[3]PLAZINSKI W， RUDZINSKI W PLAZINSKA A. Theoretical models of sorption kinetics including a surface reaction mechanism： A review[J]. Advances in Colloid and Interface Science， 2009， 152（1/2）： 213.

[4]TAN K L， HAMEED B H. Insight into the adsorption kinetics models for the removal of contaminants from aqueous solutions[J]. Journal of the Taiwan Institute of Chemical Engineers， 2017， 74： 2548.

[5]HO Y S， MCKAY G. Batch sorber design using equilibrium and contact time data for the removal of lead[J]. Water Air and Soil Pollution， 2000， 124（1）： 141153.

[6]HERNANDEZEUDAVE M T，BONILLAPETRICIOLET M A， MORENOVIRGEN M R， et al. Design analysis of fixedbed synergic adsorption of heavy metals and acid blue 25 on activated carbon[J]. Desalination and Water Treatment， 2015， 57（21）： 98249836.

[7]SUN B F， YUAN Y N， LI H L， et al. Wastecellulosederived porous carbon adsorbents for methyl orange removal[J]. Chemical Engineering Journal， 2019， 371（6）： 5563.

[8]BULUT E， OZACAR M， SENGIL I A. Equilibrium and kinetic data and process design for adsorption of Congo Red onto bentonite[J]. Journal of Hazardous Materials， 2008， 154（3）： 613622.

[9]KUNDU S， GUPTA A K. Arsenic adsorption onto iron oxidecoated cement （IOCC）： Regression analysis of equilibrium data with several isotherm models and their optimization[J]. Chemical Engineering Journal， 2006， 122（1/2）：93106.

[10]MARTINS A C， PEZOTI O， CAZETTA A L， et al. Removal of tetracycline by NaOHactivated carbon produced from macadamia nut shells Kinetic and equilibrium studies[J]， Chemical Engineering Journal. 2015， 260：291299.

[11]MCKAY G. Design models for adsorption systems in wastewater treatment[J]. Journal of Chemical Technology and Biotechnology， 1981， 31（1）：717731.

[12]YAO Y J， HE B， XU F F， et al. Equilibrium and kinetic studies of methyl orange adsorption on multiwalled carbon nanotubes[J]. Chemical Engineering Journal， 2011， 170（1）：8289.

[13]ZACAR M， SENGIL I A. A two stage batch adsorber design for methylene blue removal to minimize contact time[J]. Journal of Environmental Management， 2006， 80（4）： 372379.

[14]ZACAR M， ENGL I A. Twostage batch sorber design using secondorder kinetic model for the sorption of metal complex dyes onto pine sawdust[J]. Biochemical Engineering Journal， 2004， 21（1）：3945.

收稿日期：20210621網络出版日期：20211021

基金项目：山东省自然科学基金项目（ZR2020ME057）

作者简介：孙宝芬（1980-），女，山东无棣人，讲师，博士，主要从事纺织废弃材料的再利用、印染污水处理技术及新型复合材料制备与应用等方面的研究。