考虑微观效应的致密多孔介质分形渗透率模型

吴 兵 陈 希 田 坤 乔向阳 王永科 辛翠平

（1. 陕西延长石油（集团）有限责任公司研究院，陕西 西安 710075；2. 中国石油新疆油田公司工程技术研究院，新疆 克拉玛依 834000）

0 引 言

了解致密多孔介质中的渗流特征对非常规油藏的开发具有重要意义。致密多孔介质有着复杂的微观结构，孔隙表面与流体分子之间的相互作用导致流体滑动和流体物理性质不均匀分布。在润湿性的致密多孔介质中，相互作用会引起负滑移现象，用滑移长度表示。滑移长度取决于边界区域的厚度以及孔隙中黏度和密度的分布。以上机制导致致密多孔介质中流体的渗流特征与经典达西定律的偏离，并显示出非线性渗流特征［1‐10］。

关于非线性渗流特性目前有3 类模型：分段模型、多参数模型和分形模型。分段模型是最常见的模型，它将流动阶段分为3 个部分，非线性流动阶段由一条曲线描述，在试井和数值模拟中被广泛应用，但压力梯度较小时模型不适用。多参数模型是从实验拟合结果获得的不同系数，以描述非线性渗流阶段［11‐14］；邓英尔等［15］提出了压力梯度的隐式渗流速度表达式，但是模型的某些参数没有明确的物理意义；时宇等［16］提出了考虑边界层效应的两参数模型，但没有考虑实际的曲折流动路径。通过引入孔隙分形维数和曲折分形维数来考虑孔隙半径分布和流动路径的曲折性，分形理论在描述致密多孔介质孔隙结构的复杂性有一定的优势。目前已经建立了一些分形渗流模型，J.C.Cai［17］基于毛细管束模型提出了塑性流体的分形渗流模型，但是没有考虑边界层的影响，S.Huang 等［18］的模型引入了边界层效应，但没有考虑滑移长度和流体物理性质的不均匀分布。

此前的研究提出的非线性渗流模型，能够描述不同条件下的渗流特征，但没有综合考虑边界层效应和微观效应的影响。基于毛细管束模型，本文提出了致密多孔介质中流体传输的分形模型，可以准确表征致密多孔介质的有效渗透率，为致密油藏的开发和数值模拟提供参考。

1 模型建立

1.1 流体物理性质的不均匀分布

当涉及到微纳米级孔隙时，无滑动边界不再适用，流体在孔隙表面会发生负滑移现象，即流体分子能以一定的速度运动。孔隙表面的滑移速度与边界区域的厚度有关，还与相互作用引起的流体黏度的分布有关。当流体是水时，若孔隙表面为亲水性，孔隙表面施加的吸引力将增加流动阻力并降低滑动速度；若孔隙表面为疏水性，孔隙表面和流体的相互作用变成排斥力，将减小流动阻力并增加滑动速度。滑移速度用滑移长度来表征，即

式中：vs——滑移速度，m s；ls——滑移长度，μm；v——沿流动方向的速度，m s；z——沿径向方向的距离，m；r0——某一具体的半径，μm。

流体物理特性的非均质分布可以简化为体相区域和边界区域（图1 （a）），曲折特性（图1（b））将通过分形缩放理论在1.3 节中讨论。孔隙表面和流体相互作用仅影响边界区域的物理性质，不影响体相区域的物理性质。

图1 实际流动行为的简化和曲折表征Fig.1 Simplification of actual flow behavior and tortuous characterization

边界区域中流体黏度与接触角的相关表达式为

式中：μi——边界区域黏度，mPa∙s；μb——体相区域黏度，mPa∙s；θ——接触角，（°）。

滑动长度与边界区域厚度、体相区域黏度和边界区域黏度之间的表达式为

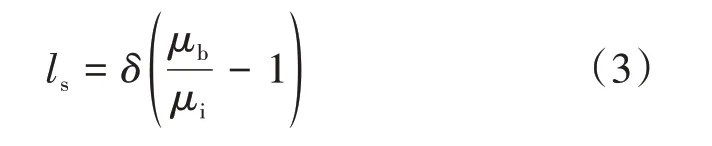
式中δ——边界区域的厚度，μm。

流体密度与接触角之间的关系为

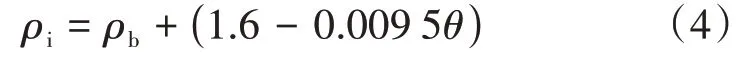
式中：ρi——体相区域密度，kg/m3；ρb——边界区域密度，kg/m3。

边界区域的厚度可以通过实验方法或分子模拟来确定。在耗散粒子动力学（DPD）模拟和实验结果的基础上，X.F.Tian 等［19］提出了流体黏度、孔隙半径和压力梯度的综合表达式为

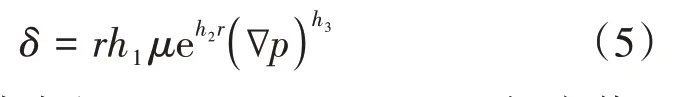
式中：r——孔隙半径，μm；h1，h2，h3——恒定值，h1= 0.257 63，h2= −0.261，h3= −0.419；μ—— 黏度，mPa∙s；∇p——压力梯度，MPa m。

S.Huang 等［18］将Tian 的表达式修改为

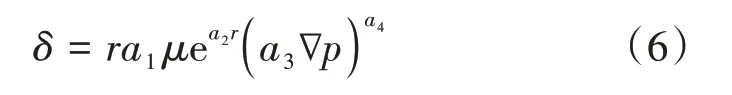
其中h1=a1a3a4，h2=a2，h3=a4

式中：a1——黏度的影响系数，(mPa·s)−1；a2——喉部半径的影响系数，μm−1；a3——压力梯度的影响系数，(MPa m)−1；a4——量纲为1 的压力梯度影响指数。

1.2 微纳米级孔隙中的流体流动

边界区域和体相区域同时存在2 个速度场，并且微纳米孔隙内液体的速度分布是连续的。在边界区域，由于孔隙表面的滑移现象，流体速度公式为

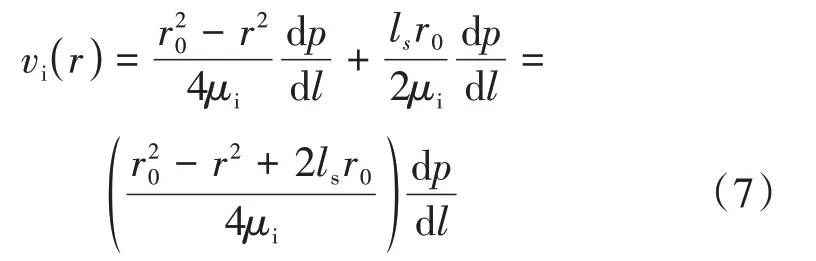
式中：vi(r)——边界区域的流体速度，m s；p——流体压力，MPa；l——流体流动方向的距离，μm。

考虑不均匀的黏度和边界区域的厚度，可以通过公式计算体相区域的速度分布，即

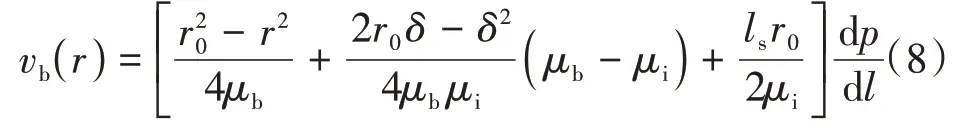
式中vb(r)——体相区域内的流体速度，m s。

计算边界区域和体相区域内的流体质量流量，对式（7）和式（8）进行积分。

边界区域贡献的质量流量公式为

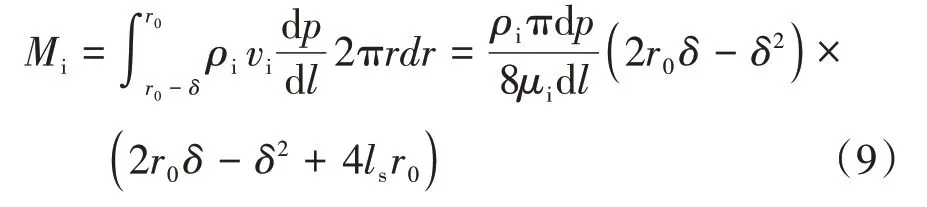
式中Mi——边界区域贡献的质量流量，kg/s。

体相区域贡献的质量流量公式为

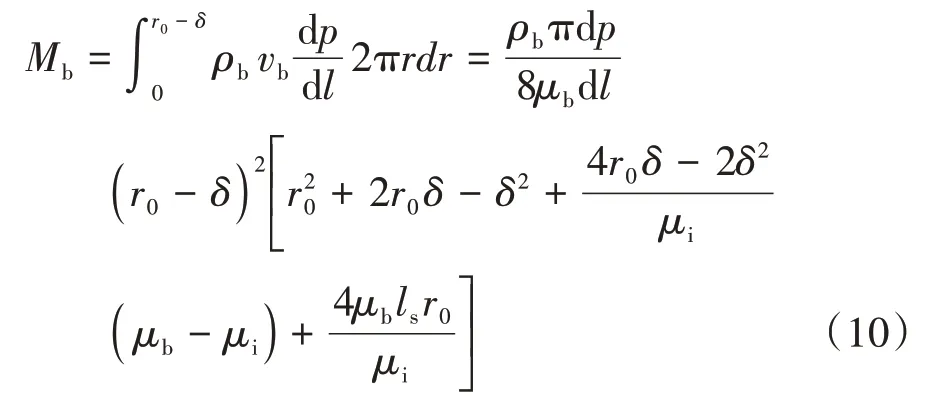
式中Mb——体相区域贡献的质量流量，kg/s。

计算总质量流量对式（9）和式（10）求和，即

式中M——总质量流量，kg/s。

1.3 分形理论

如图2 所示，多孔介质孔隙的分布符合分形规律，累计的孔径分布表达式为

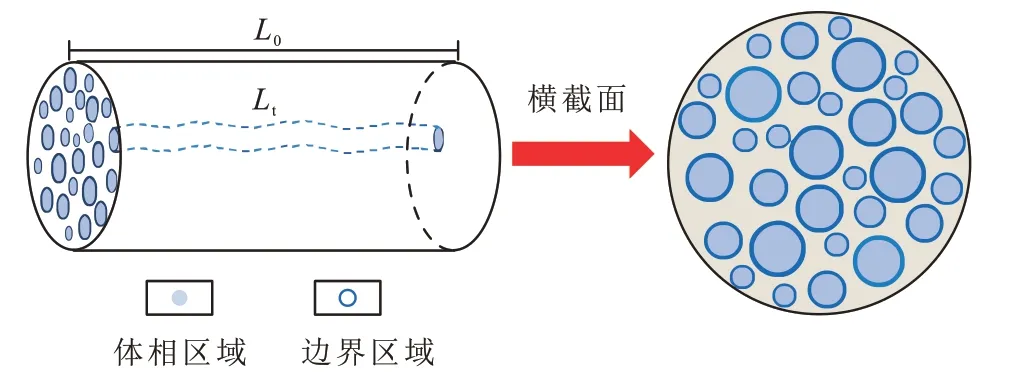
图2 实际岩心样品中边界区域和体相区域的存储特征Fig.2 Storage characteristics of interfacial region and bulk region in actual core samples

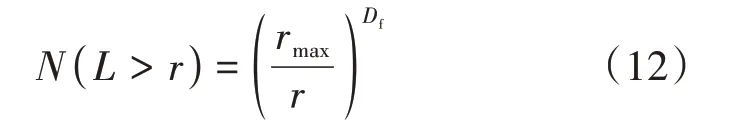
式中：N(L>r)——孔隙半径大于r的孔隙的数量；rmax——最大孔隙半径，μm；Df——孔隙分形维数（本次采用二维分形维数）。

Df计算公式为

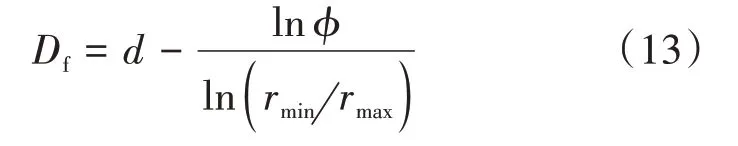
式中：d——欧几里得维数，二维中d= 2；ϕ——孔隙度；rmin——最小孔隙半径，μm。

得到半径大于rmin的孔隙的总数为

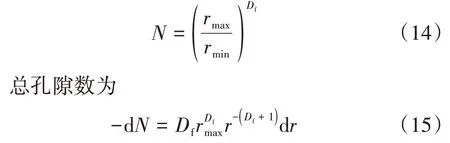
对于二维空间，孔隙模型的横截面面积计算公式为

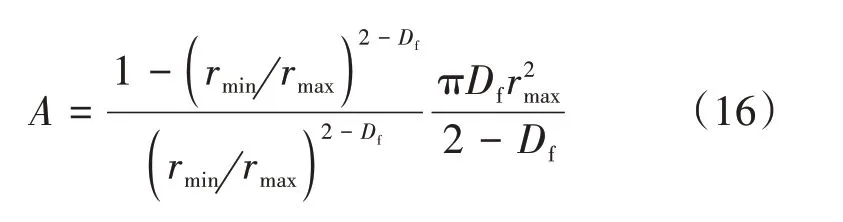
式中A——横截面面积，m2。

如图1 所示，致密多孔介质中的流动路径被认为是具有不同横截面尺寸的曲折管。由于流路的曲折性质，实际长度Lt通常大于特征长度L0（图2），根据自相似分形定律，实际长度Lt为

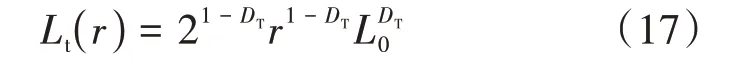
式中：Lt( )r——实际长度，m；L0——特征长度，m；DT——曲折分形维数，DT越高，流动路径越曲折。

式中：τave——平均迂曲度；rave——平均孔隙半径，μm。

1.4 致密多孔介质中渗透率的分形模型

边界区域的厚度通常很小，可以忽略二次项，三次幂项和第四次幂项，将边界区域贡献的质量流量简化为

结合式（15）、式（24），微纳米级孔隙的流体总质量流量计算公式为

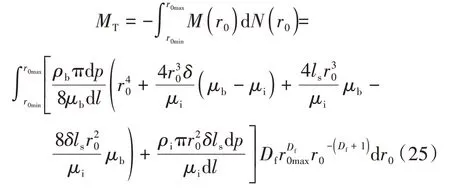
考虑到致密油藏流动路径的曲折性质，并经过进一步的公式推导，得

式中Ke——致密多孔介质的有效渗透率，10−3μm2。

有效渗透率与压力梯度的厚度、孔隙分形维数、曲折分形维数、流体黏度和密度的异质分布有关。根据式（2）、式（4），它也直接受接触角的影响，即

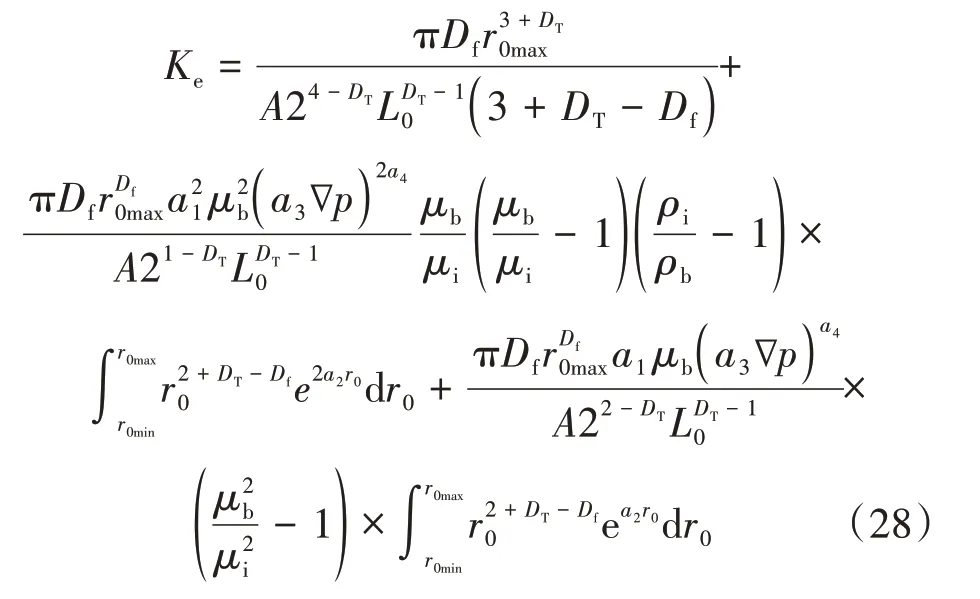
B.M.Yu 等［20］提出了不考虑多种机制的分形渗透率模型，而S.Huang 等［18］提出了考虑边界层效应的分形渗透率。如不考虑多种机理，则将模型简化为Yu 模型。如仅考虑边界层效应，可以将模型简化为Huang 模型，即

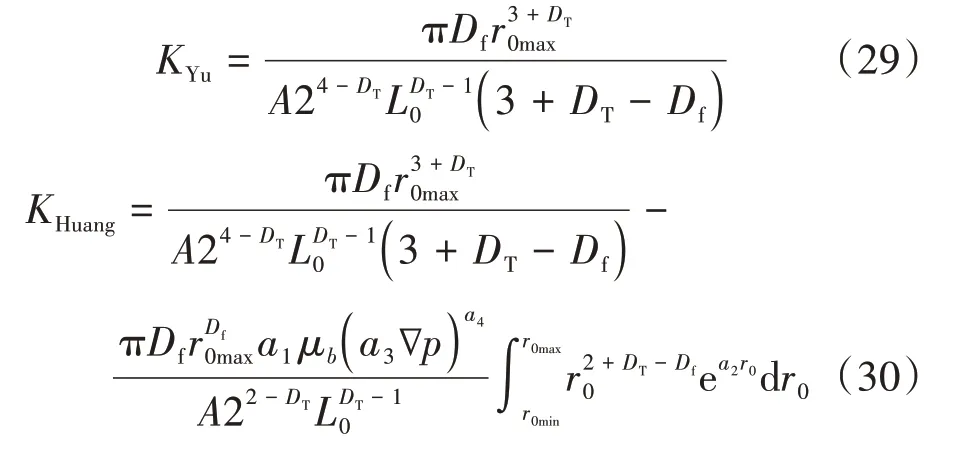
2 模型验证

杨正明等［21］在进行特低渗透油藏非线性流渗流数值模拟研究时，通过恒速压汞实验获得了具有超低渗透率的岩心样品的孔喉分布。该实验中，大多数岩心最大喉道半径小于6 μm，流体的黏度为1.005 mPa∙s，完整的实验程序和高精度的实验设备保证了实验数据的高精度，且该实验数据已用于验证S.Huang［18］的渗透率模型。

本次模型的验证也采用上述实验数据，用有效渗透率Ke与绝对渗透率K的比值对模型进行验证，如果模型计算结果能够成功地捕获实验数据，则可以验证模型的可靠性。选用5 块不同气测渗透率值的岩心实验数据，模型计算应用的参数见表1。模型计算预测结果（线）与杨正明实验数据（点）的比较如图3 所示，该模型的预测结果与实验数据一致，模型的结果与实验数据具有相似的变化趋势，有效渗透率和绝对渗透率的比值随着压力梯度而增加。尽管预测结果与实验数据显示出良好的相关性，但提供更多模型计算需要的参数（如孔隙度、接触角、曲折分形维数、孔隙分形维数等），可以进一步提高模型计算的准确性。

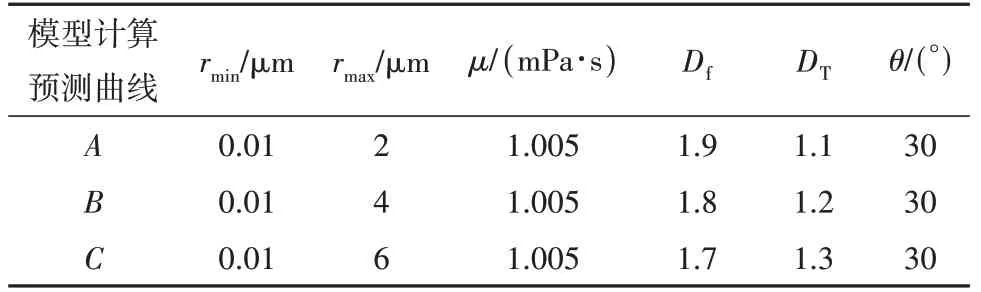
表1 模型计算中应用的相关参数Table.1 Related parameters applied in the model’s calculations

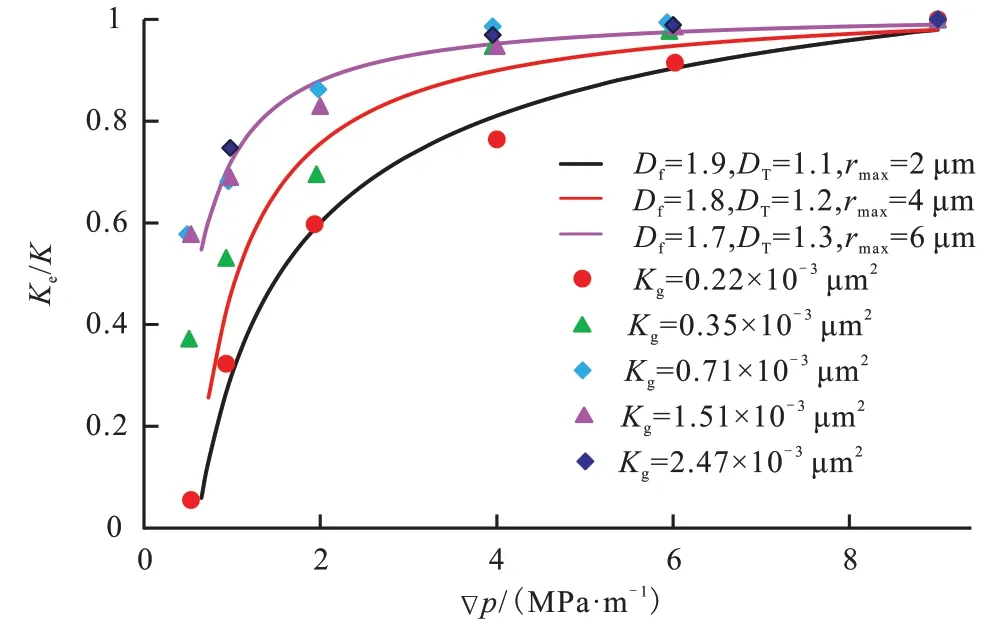
图3 实验数据（点）与模型的预测结果（线）对比Fig.3 Comparison between data collected from experi‐ments(plots)and the model’s prediction results(lines)

3 参数敏感性

3.1 润湿性和压力梯度

图4 为不同接触角对有效渗透率的影响情况，不同接触角下的计算结果是本次模型计算结果，Huang 模型和Yu 模型均未考虑到接触角。因为Huang 模型中边界层效应仅被视为有效孔隙半径和质量流量的减小，故本次模型计算的结果比Huang模型高。Yu 模型忽略了边界层效应和微观效应，故本次模型和Huang 模型的结果都比Yu 模型小。

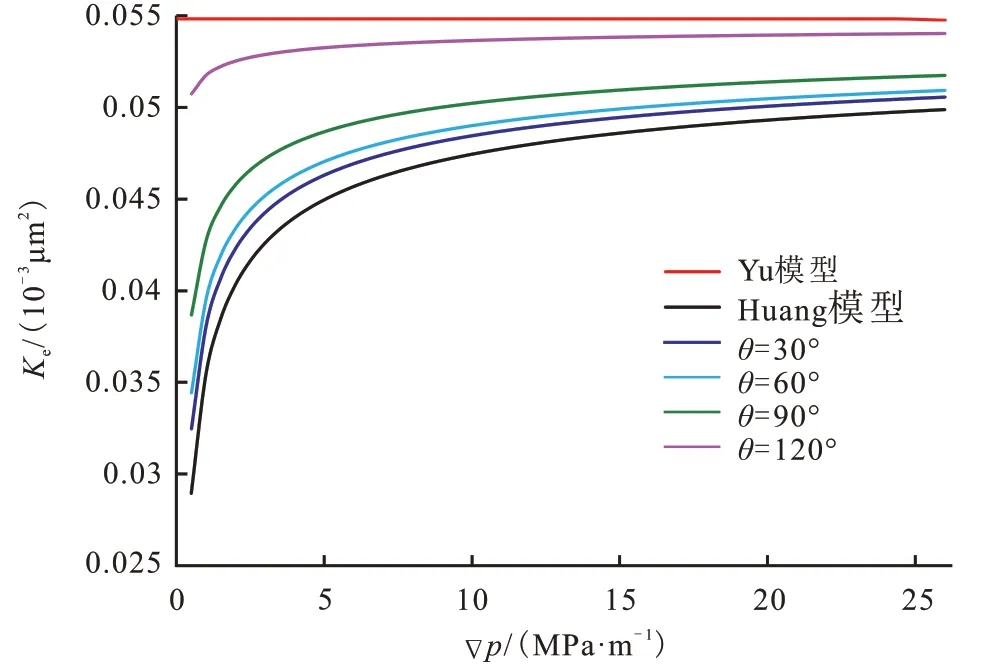
图4 不同接触角对有效渗透率的影响Fig.4 Effects of contact angle on effective permeability

有效渗透率随着压力梯度的增加而增加，当压力梯度较大时趋于稳定。这是由于压力梯度的增加会导致边界区域的厚度变小，滑移长度增加；当压力梯度非常小时，流体不能克服由孔隙表面和流体分子之间的相互作用力，导致有效渗透率非常小。随着压力梯度的增加，边界区域的厚度逐渐稳定，有效渗透率的值也趋于恒定。

有效渗透率随着接触角的增大而增大，这是因为接触角越大，边界区域和体相区域中流体黏度差越小，滑移长度越大，由孔隙表面引起的吸引力越小，有效渗透率值越大。故润湿性在致密多孔介质中的液体传输能力中起着至关重要的作用，改善润湿性是提高致密油藏产量的有效措施。

3.2 流体黏度

如图5 所示，流体黏度对有效渗透率有显著影响，并且可以观察到启动压力梯度。有效渗透率随着流体黏度的增加而降低，这是因为黏度越大，边界区域厚度越大，导致渗透率的降低。

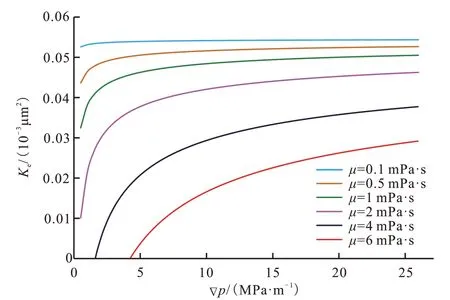
图5 流体黏度对有效渗透率的影响Fig.5 Effects of fluid viscosity on effective permeability

如图6 所示，启动压力梯度存在并且随流体黏度而变化。一定的压力梯度下，有效渗透率随流体黏度的增加而减小。当流体黏度达到一定程度时，压力梯度较低时流体无法克服表面与液体之间的相互作用力。增加压力梯度可以提高致密多孔介质中的流体流动能力。

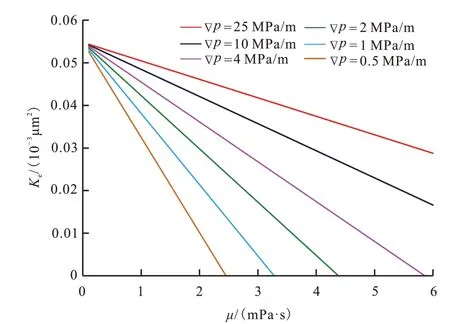
图6 压力梯度对有效渗透率的影响Fig.6 Effects of pressure gradient on effective permeability

3.3 孔隙分形维数和曲折分形维数

从图7 中可以看出，有效渗透率随着孔隙分形维数的增大而增大。因为较大的分形维数意味着孔隙数增加，孔隙表面与流体之间相互作用的影响虽然更加明显，但越来越多的孔隙仍然可以为流体提供传输路径，所以当孔隙分形维数增加时，压力梯度的影响将变大。

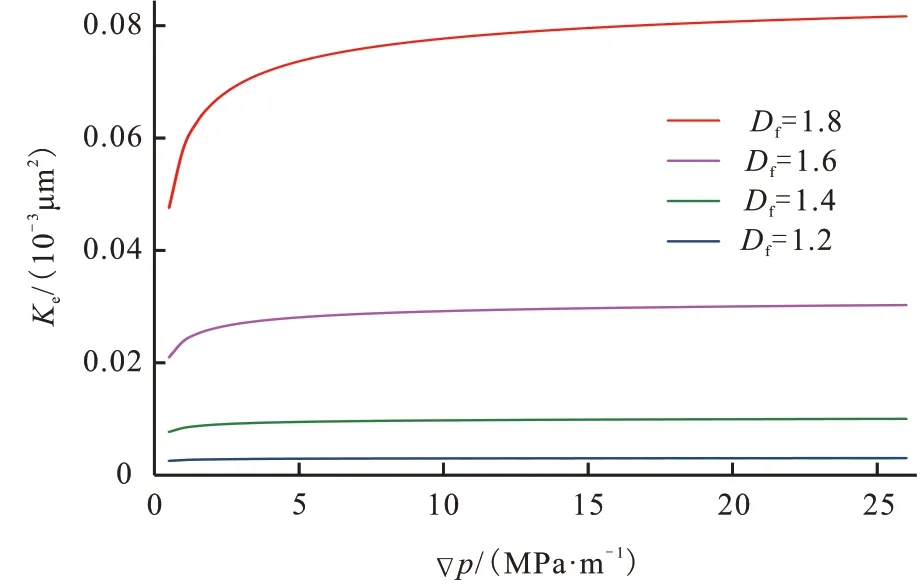
图7 孔隙分形维数对有效渗透率的影响Fig.7 Effects of pore fractal dimension on effective permeability

图8 显示有效渗透率随曲折分形维数的增加而降低，这是因为曲折分形维数越高，意味着曲折的流路越多，由于长流路的阻力越大，有效渗透率就越低。当曲折分形维数较大（DT>1.6）时，压力梯度的影响会降低。

图8 曲折分形维数对有效渗透率的影响Fig.8 Effects of tortuosity fractal dimension on effective permeability

4 结 论

（1）通过考虑边界层效应、负滑移现象和流体物理性质不均匀分布等微观效应，基于毛细管束模型和分形理论，建立了新的渗透率模型来表征致密多孔介质中流体的传输能力，并用高精度实验数据验证了模型的可靠性。

（2）致密多孔介质中流体有效渗透率随着压力梯度的增大而增大，随着接触角的增大而增大，随着黏度的增大而减小；有效渗透率直接受到微观孔隙结构的影响，与孔隙分形维数呈正相关，与曲折分形维数呈负相关。