含反馈环的电动飞机驱动系统可靠性分析方法

江秀红 ,李佳欣 ,刘彦娟,3 ,王玉颖

(1.辽宁锐翔通用飞机制造有限公司,辽宁 沈阳 110036;2.沈阳航空航天大学 电子信息工程学院,辽宁 沈阳 110036;3.辽宁通用航空研究院,辽宁 沈阳 110036)

0 引言

电驱动系统为电动飞机提供前进动力,一般由电源、控制器、驱动板、电机等一系列零部件组成。永磁同步电机(PMSM)以其高效、高功率密度、良好的调速性能和较低的振动噪声等优点,成为通用电动飞机的首选动力电机。电驱动系统的可靠性和性能直接影响飞机的飞行质量和飞行安全,倘若出现故障且没能及时排除,其后果可能是机毁人亡。因此对电动飞机的驱动系统进行可靠性分析十分必要,不仅可以暴露潜在的设计缺陷和薄弱环节,为改进系统设计、实现系统可靠性水平持续增长提供技术支撑,而且可以在短期内获知驱动系统的可靠性水平,为系统故障诊断和健康管理提供数据。

常用的系统可靠性分析方法有故障树分析、可靠性框图、故障模式影响及危害性分析、成功流(GO)法等。GO 法是一种面向成功的系统可靠性分析方法,尤其在分析多状态、有时序及流程性系统时具有一定优势。PMSM 驱动系统作为一种有电流流动的系统,非常适合采用GO 法进行可靠性分析。但驱动系统中一般存在电流、速度等多个反馈环,而GO 法无法处理这些反馈环。以往分析含反馈环的系统可靠性时,一般直接将反馈环断开,这虽然使分析得以进行,但降低了分析结果的可信度。近年来也涌现了一些针对反馈的处理方法,兰雪等采用布尔代数解决了GO-FLOW 图中不允许存在循环的问题,但该方法不适用于GO法。Yi 等创建了一种基于GO 法的双输入闭环反馈的新函数运算符,并根据马尔可夫获得定量算式,然而这是一个复杂的矩阵方程,有时难以获得解析解。李景奎等将模糊GO 法和枚举法应用到闭环系统的可靠性分析中,但对于复杂系统运算量将大大增加。

本文基于GO 法进行PMSM 驱动系统的可靠性分析,并通过设置反馈信号为未知量,建立联立布尔方程组来获得各信号流的可靠性数据。与直接断开反馈的分析结果对比,本文所提方法可有效提高含反馈系统可靠性分析的精度。

1 PMSM 驱动系统可靠性建模

1.1 PMSM 驱动系统组成

某通用电动飞机的PMSM 驱动系统主要由电源(电池组)、TMS320F28335 DSP 为核心的控制器、2SP0115T 构成的IGBT 驱动板、FF600R07ME4 构成的IGBT 三相桥式逆变器以及60 kW 的PMSM 组成,所有器件均为工业级标准。含反馈的PMSM 驱动系统结构原理图如图1 所示。

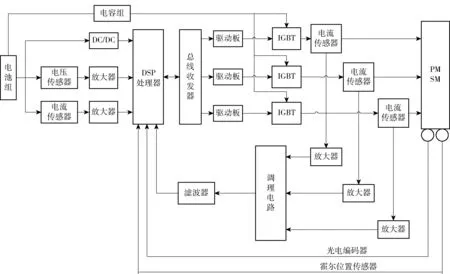
图1 含反馈的PMSM 驱动系统结构原理图Fig.1 Schematic diagram of PMSM drive system with feedback

电池组提供系统所需电源,连接到电容组分配板和IGBT 逆变器,构成驱动主回路。DSP 处理器作为控制核心,输出的高精度脉冲宽度调制经过总线收发器与外部IGBT 驱动板相连,通过三相IGBT的通断实现电机转速和转向控制。母线电压经电压传感器输出为差分信号,然后经放大器转为单端输出后进入DSP 处理。电流信号是实现电机精准控制的重要参考,三相输出电流经放大调理、滤波后输入DSP 处理器,母线电流也经传感器采集后送入DSP 处理器。光电编码器可以获得电机速度、旋转方向和绝对零位,霍尔位置传感器的差模信号传送给DSP 处理器处理。

图1 存在多个反馈环,如电流传感器采集的三相输出电流经放大、调理后又输回DSP 处理器,霍尔传感器和光电编码器采集的速度等信息也反馈回DSP 处理器。断开反馈后的PMSM 驱动系统结构原理图如图2 所示。

图2 断开反馈后的PMSM 驱动系统结构原理图Fig.2 Schematic diagram of PMSM drive system without feedback

图2 可直接利用GO 法建立系统可靠性模型GO 图并进行分析。

1.2 PMSM 驱动系统可靠性模型

利用GO 法建立系统GO 图非常方便,只需选择合适的GO 操作符将系统原理图或工程图直接翻译成GO 图即可。GO 图中的操作符代表具体的部件或逻辑关系,信号流连接操作符代表具体的物流或者是逻辑上的进程。GO 图建立后,再根据操作符的运算规则和信号流向进行GO 运算,即可完成系统可靠性的定量分析。

根据PMSM 驱动系统中各部件的功能及GO 操作符的特点,将图2 翻译成GO 图,PMSM 驱动系统的GO 图如图3 所示。

图3 中,圆圈和三角代表不同的操作符,操作符内横线前的数字表示操作符的类型,横线后的数字表示操作符的编号,箭头表示信号流向,箭头上的数字表示信号流序号。各操作符的类型、代表的单元名称以及可靠性数据按编号列于表1。

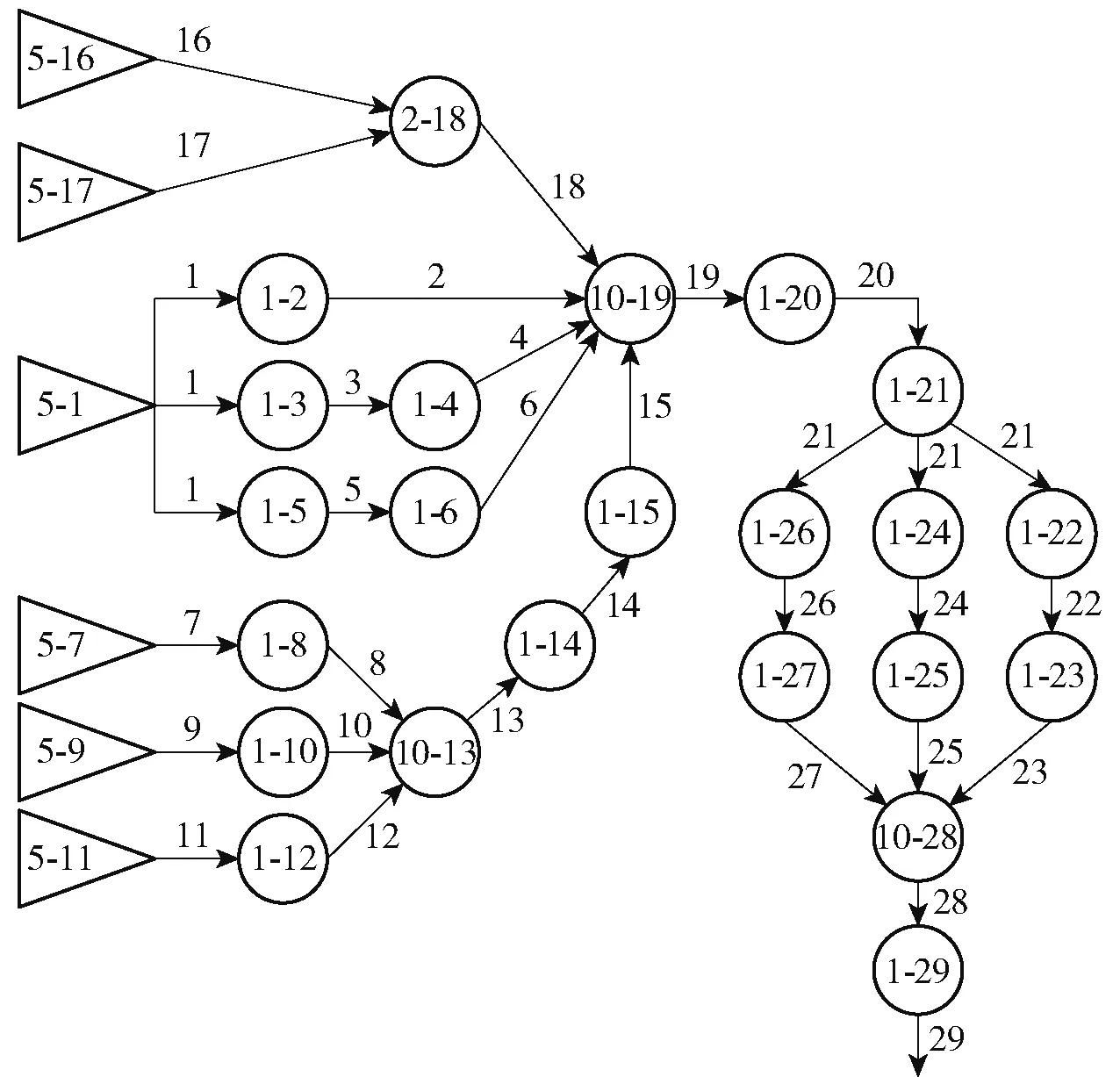
图3 PMSM 驱动系统的GO 图Fig.3 GO diagram of PMSM drive system

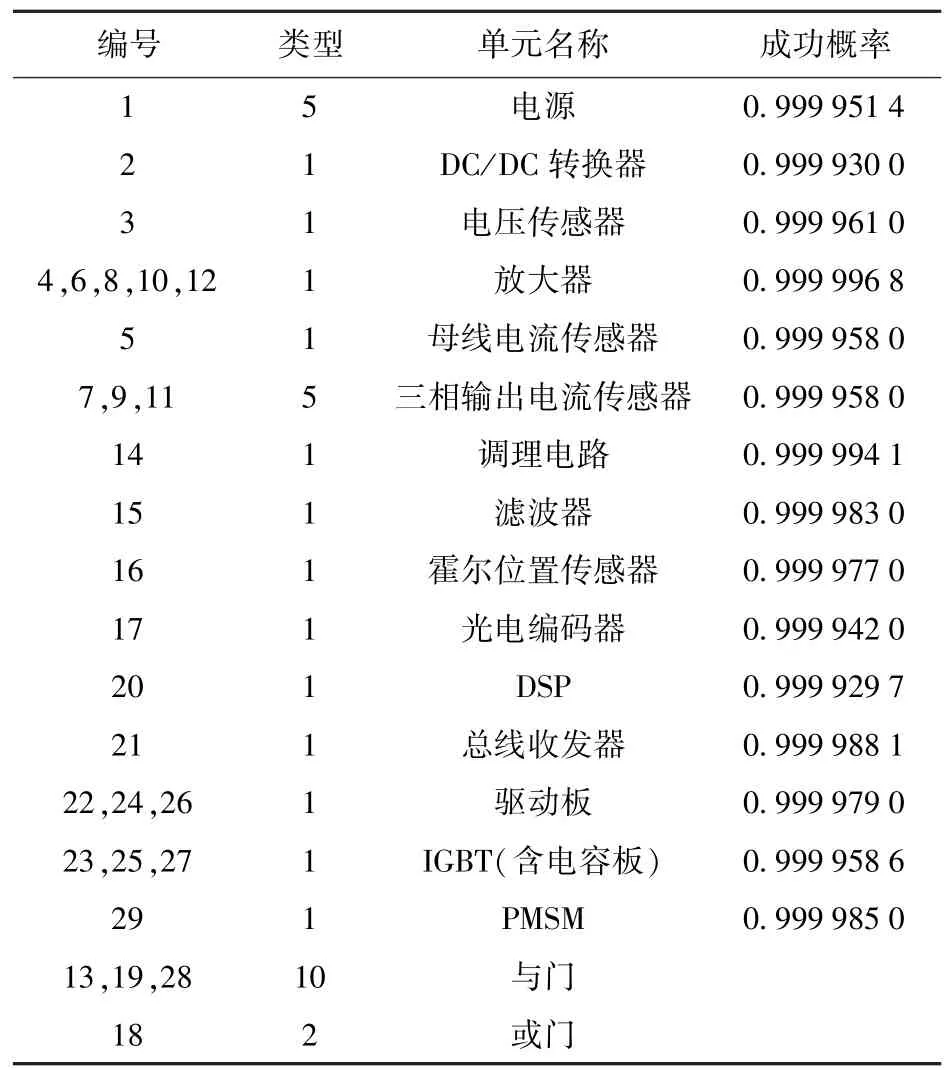
表1 驱动系统的操作符数据Tab.1 Operator data of of drive system

电源作为整个系统的驱动动力,为系统输入,因此用单信号发生器(类型5 操作符)表示。因为断开了反馈,所以三相输出电流传感器、霍尔位置传感器、光电编码器也作为类型5 操作符直接输入。DC/DC 转换器、母线电压传感器、母线电流传感器、滤波器、调理电路、DSP 处理器、总线收发器、驱动板、IGBT 和PMSM 只有成功和故障两种状态,因此用两状态单元(类型1 操作符)表示。霍尔位置传感器和光电编码器若有一个发生故障,系统也能安全工作,因此用或门表示二者的关系。汇集到DSP控制板的信号缺一不可,因此用与门(类型10 操作符)表示信号之间的逻辑关系。同理,3 个IGBT 之间也是与的关系。

2 反馈环处理的基本思路

表1 数据代入图3,再沿信号流流向按GO 操作符运算规则即可获得不含反馈的系统可靠性。但直接断开反馈改变了原系统的逻辑关系,此时获得的分析结果可信度并不高。下面基于逻辑代数提出一种反馈环的解决方法。

图4 所示为含反馈的两单元系统,单元A 的输出作为单元B 的输入,B 的输出又反馈回来作为A的输入。

图4 含反馈的两单元系统Fig.4 Two-component system with feedback

假设A、B 均为两状态单元,对应布尔变量分别为和,信号流1 和2 对应的布尔变量为和,每个变量取值为1(成功)或0(故障),则

根据布尔代数关系=,(1)式等价于布尔方程=·,=·,因此

即单元A 和单元B 同时成功时信号流2 才成功。若和分别表示单元和信号流的成功概率,则信号流2 处于成功的概率为

又因为=·=(·)·=·,所以信号流1 成功的概率为

若对图4 直接断开反馈进行计算,则两个信号流的成功概率分别为

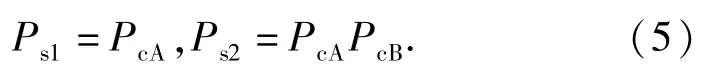
可见,不考虑反馈时,信号流1 的可靠性数据并不准确。

再以一个含反馈或门的三单元系统(见图5)为例进行说明。图5 中D 为系统输入,E 为或门(失效概率为0),F 为两状态单元。

图5 含反馈和或门的三单元系统Fig.5 Three-component system with feedback and OR gate

设、分别为系统输入以及两状态单元对应的布尔变量,则信号流3 对应的布尔变量为

(6)式等价于布尔方程=·+,、为布尔代数,解为=+或=,即=(1 -)·+·=或=·。换算成对应的概率,则

或

又因为一个系统或部件的可靠性是其可用性能的最大值,所以=。这个解与实际是符合的,因为根据图5 的连接方式,只要单元F 安全工作,系统就能可靠运行。

若断开反馈直接计算,则信号流3 的成功概率为=,进一步说明了断开反馈降低了可靠性分析结果的可信度。

对于任意含反馈的系统,可按照如下步骤对反馈环进行处理:

寻找系统中的反馈,设置反馈变量,个反馈则设置个反馈变量,,…,X。

将反馈从反馈引出端断开,并将反馈变量作为之前反馈引入端的一个输入。

沿着信号流的流向列写各反馈变量的表达式,得到个联立逻辑代数方程组。

求解该方程组,获得反馈变量,,…,X,进而求得各信号流的可靠性数据。

仍以图5 为例,反馈从信号流3 引出,因此设信号流3 为,并将此信号作为系统一个输入,设置反馈变量如图6 所示。

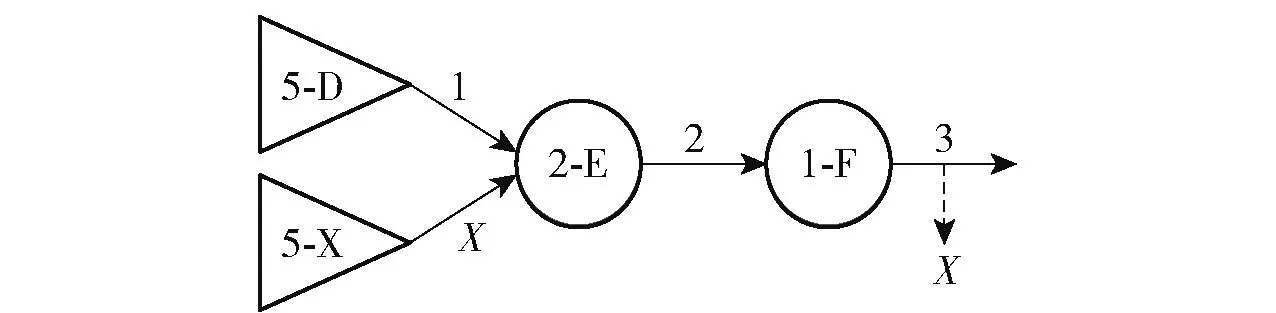
图6 设置反馈变量Fig.6 Setting of feedback variable

此时图6 不含反馈,按信号流向,有

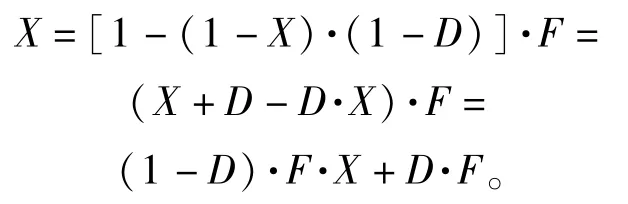
求解此逻辑方程,得到=或=·(舍去),再由即可求得其他信号流的可靠性值。

3 PMSM 驱动系统可靠性分析

3.1 不考虑反馈的系统可靠性分析

根据图3,去掉反馈的系统GO 图,进行可靠性定量计算,参考表1 各操作符成功概率,则信号流的布尔变量S、系统中各单元的布尔变量C计算过程如下:

1)信号流2:

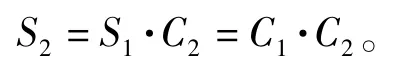
2)信号流4:

3)信号流6:

4)信号流15:

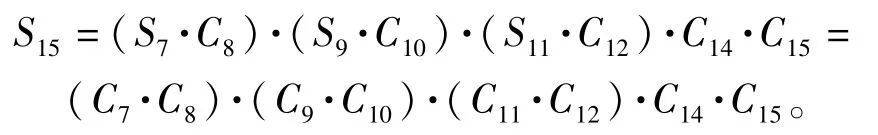
5)信号流18:

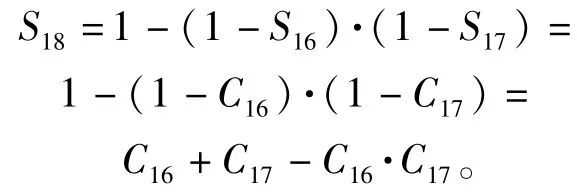
6)信号流20:

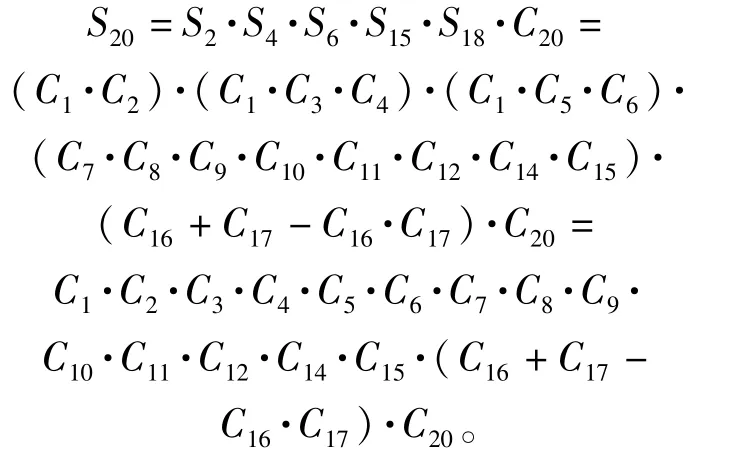
7)信号流29:

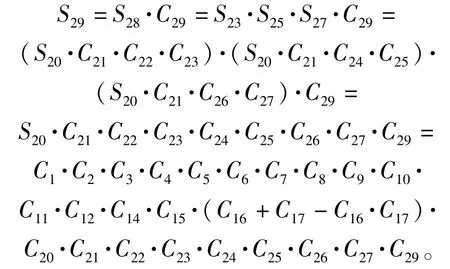
代入相应成功概率,则信号流29 的成功概率为

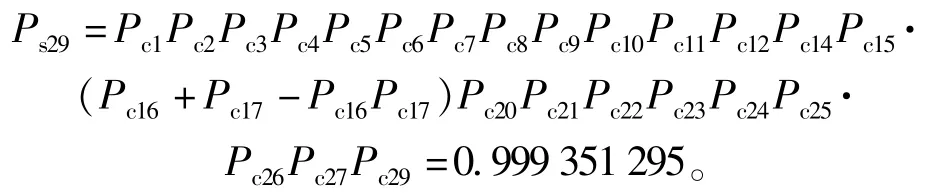
因此,不考虑反馈情况下系统的成功输出概率为0.999 351 295。

3.2 考虑反馈的系统可靠性分析

1)信号流2、4、6 不含反馈变量,因此计算结果与不考虑反馈的一致。

2)信号流15:

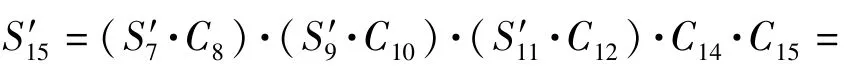
3)信号流18:

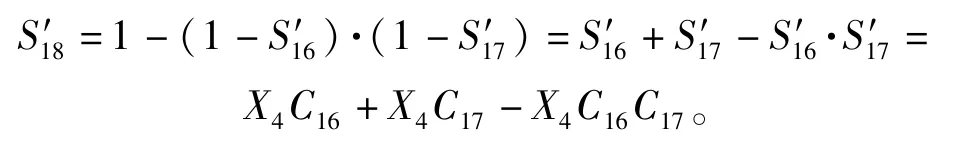
4)信号流20:

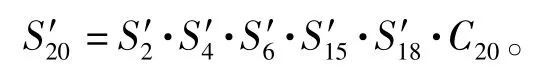
5)信号流23:

6)信号流25:

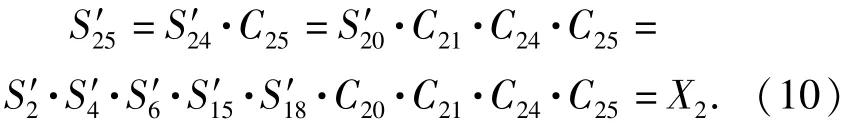
7)信号流27:

8)信号流29:

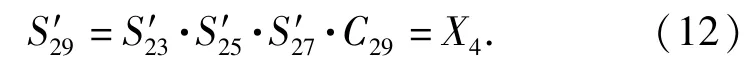
方程(7)式～ (11)式构成了含、、、4 个未知量的方程组,对其求解即可得到各反馈变量。

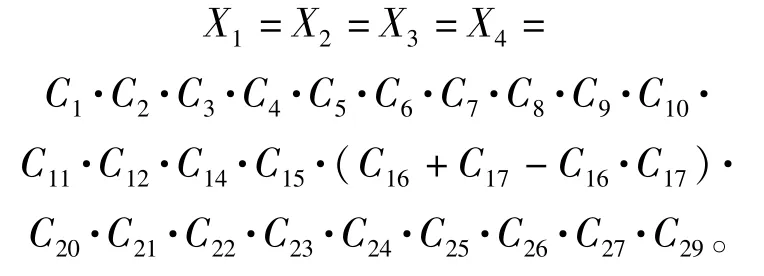
将对应成功概率代入,各信号流的成功状态概率在断开反馈和含反馈两种情况下计算结果对比如表2 所示。

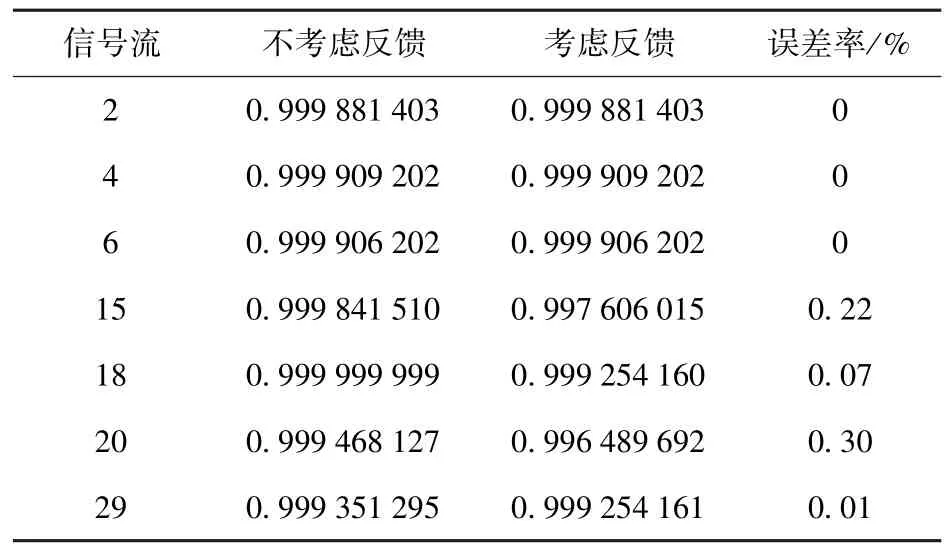
表2 两种情况计算结果对比Tab.2 Comparison of calculated results in two cases

由表2 可见,不考虑反馈时,由于改变了系统的逻辑连接关系,导致部分信号流的可靠性分析结果并不准确。表2 中信号流2、4、6 不存在误差是因为这3 个信号中不含有反馈信号。

4 结论

为提高含反馈环的电驱动系统可靠性分析的准确性,本文提出了一种建立布尔方程来解决反馈环的方法。将反馈从反馈引出端断开,作为反馈引入端的一个输入变量,沿着信号流的流向,结合GO 法运算规则,列写各反馈变量的表达式,得到含有反馈变量的联立方程组。求解该方程组获得反馈变量表达式,进而求得系统的可靠性数据。应用该方法对某PMSM 驱动系统进行可靠性分析,并与断开反馈的分析结果进行对比,表明了所提方法是可行有效的。