输电线路桩基典型力学参数插值精度研究

苏朝晖 丁士君 崔强 刘广 张振华

摘要：输电线路跨度大、分布广的特点极大地增加了输电线路基础建设过程中的勘测工作量。在已知部分输电线路勘测点位数据的情况下，采用克里金、样条函数和反距离权重插值等方法对输电线路其余点位桩基的主要力学参数进行了合理预测，详细比较了插值误差，分析了不同插值方法在输电线路桩基参数插值过程中的主要特点，并分析了幂参数取值对反距离插值方法进行极限端阻力插值的精度的影响。结果表明：采用反距離权重法对条带状分布的参数进行插值时，概念简单，编程容易，插值精度也在合理范围内;随着幂参数的增大，插值精度逐步提高。

关 键 词：输电线路; 桩基勘测; 插值方法; 承载力; 内摩擦角

中图法分类号： TU452

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2022.04.018

0 引 言

在地质领域，为获得高精度的地理要素空间分布信息，各种空间插值方法已被广泛应用。如采用不同插值方法进行地下水位等值线图绘制[1]，秦俊桃等[2]以西北干旱内陆区石羊河流域中游武威盆地为例，分析比较了地统计学方法中常用的8种空间插值方法在地下水位插值中的应用效果。这些插值方法中，克里金（Kriging）插值是地质参数插值过程中应用十分广泛的插值方法，可以通过不同变异函数模型来确定最优的插值方式[3-6]。张靖[7]根据地表信息点云数据进行空间插值，得出克里金插值精度最高的结论，并且其在可视化上优于其他方法。

近些年来，插值方法也被应用于其他领域，以便快速地获取需要的数据。如插值方法被用于表层土样磁性参数的获取和预测[8-9]，研究成果表明普通克里金方法具有更好的适用性。李增兵等[10]用反距离权重法和普通克里金法对有机质、有效磷、有效硼、有效锌、速效钾进行插值，通过对比分析得出在县域耕地地力评价中选择反距离权重方法对养分空间插值是最佳的。还有学者采用改进的克里金算法研究GPS 水汽插值，实验结果表明改进的克里金插值算法能够充分考虑高程和距离对大气插值的影响，改进的算法较之前算法具有优越性[11]。

随着中国电网建设数字化、智能化时代的到来，对于输电线路建设的数据挖掘和应用工作将会越来越丰富，充分利用好这些历史勘察数据，结合现有地质参数插值方法，对未知勘测点位的主要地质和力学参数作出合理预估，是高效推进输电线路建设、发挥已有工程数据和信息价值的重要手段和举措。基于此，本文在已知部分输电线路勘测点位数据的情况下，采用克里金、样条函数和反距离权重插值方法对输电线路其余点位的主要力学参数进行合理预测，并详细比较了插值误差，分析了不同插值方法在输电线路桩基参数插值过程中的主要特点。

1 工程概况和研究方法

1.1 工程背景

本文研究对象为特高压直流输电线路工程，截取部分线路进行分析。该线路途经地貌单元属低山丘陵，局部为山间凹地，山间凹地地段地形平坦，分布有较多“U”形冲沟，冲沟一般较浅。低山丘陵地段地形略有起伏，大部分山形呈圆形，局部山形呈倒“V”形。海拔高程1 920～2 190 m，该段线路长度29.929 km。

本文所用数据来源于沿线代表性地段的土工试验成果、标准贯入试验成果、动力触探成果及颗粒分析成果表等基础资料。参考该地区已建工程的岩土工程勘察资料和当地建筑经验，并结合野外勘察鉴定确定。

1.2 研究方法

工程选用点位数据共44个，分为两组，一组7个，二组37个。数量较少的一组作为验证组，以检验插值方法的准确性。需要注意的是，在选择点位时应尽量避免岩性突变地区，插值结果也仅适用于连续的地层。

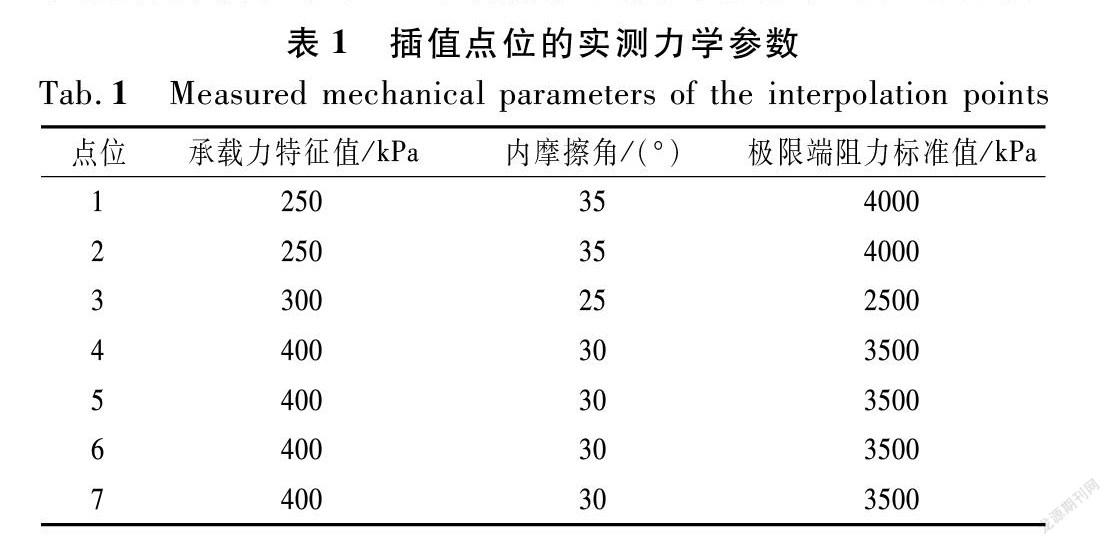
采用不同的插值方法对第二组数据进行插值。本文选取的插值方法有克里金法、反距离权重法以及样条函数法。将插值后的结果与验证组的数值进行对比，以验证插值结果的准确性。插值所用的参数，依据实际工程的需要进行选择。地质参数主要为输电线路桩基选型提供数据支撑，因此选择了3个对基础设计较为重要的参数，即承载力特征值、内摩擦角及极限端阻力标准值进行分析。验证组中各点位的力学参数如表1所列。

2 插值方法及原理

2.1 克里金插值法

克里金插值方法（Kriging）是以南非矿业工程师Krige名字来命名的一种实用空间插值技术[12]。这种方法实际上是基于数据点的大小和空间位置相互关系对未知样本点进行的一种线性无偏最优估计。

假设研究区域a上的研究变量Z（x），在点xi∈A（i=1，2，…，n）处属性值为Z（xi），则插值点x0处的属性值Z*（xi）可以用克里金插值方法表示为下式[13]：

Z*x0=ni=1wiZ（xi）（1）

式中：wi是待定权重系数。

显然，由于已知数据点之间很可能存在一定的相关关系，这种相关可以是距离相关，也可以是相对变化方向的相关。

因此，克里金插值的关键点就是求取权重系数，按照无偏估计和方差最小两个条件来确定权重系数wi（i=1，2，…，n），可得求解待定权系数wi的方程组[13]：

ni=1wiCxi，xj+μ=C（x0，xj） j=1，2，…，n

ni=1wi=1（2）

式中：Cxi，xj是变量Z（xi）和Z（xj）的协方差函数。

2.2 样条函数插值法

在有的实际问题中，要求插值曲线具有较高的光滑性，这种情况可以选用样条函数法进行插值。样条插值函数是一种特殊的插值函数，其函数由多项式分段定义，这种函数在各段节点处具有一定光滑性。样条曲线函数要求在各个连接点两端，包括连接点具有连续的函数值、一阶导函数值以及二阶导函数值。它不会出现如高次多项式插值结果可能出现的局部跳跃现象，其结果具有良好的连续光滑性和局部收敛性。常用样条插值函数为自然三次样条插值函数，其要求样条多项式的一阶导数和二阶导数在插值区域的两端相等[14]。此插值方法适用于对插值参数具有光滑性要求的情况，常用于插值渐变的水位、气压、气温等物理参数。样条函数的插值误差不太好控制，在已知点位较少时可能存在较大误差。C6FDD2D9-7822-4550-B0C0-EBE1E13B2DD8

2.3 反距离权重插值法

反距离权重法的原理比较简单，也比较符合地质参数的空间变化规律，即距离越远，样本点对目标点的影响越小。通过距离来加权系数或者影响因子，进而很好地控制插值数据的连续性，这种方法插值后生成的样本点数据与实测值完全一致，关于权重系数的计算过程也有很大可以调整的空间，插值结果精度较高。

反距离权重法插值过程采用式（3）表示[14]：

ve=nj=1wj×vj（3）

式中：wj為样本点j的权重系数;vj为样本点j的地质参数值;ve为目标点的参数估计值。

该方法中的权重系数可以根据距离来确定，一般情况下可以采用式（4）～（5）求解各样本点j的权重系数[15-16]。

wj=d-pejnj=1d-pej（4）

nj=1wj=1（5）

式中：dej为目标点与样本点j之间距离，可以通过求均方根预测误差的最小值确定其最佳值。p为幂参数，幂参数是一个正的实数，通过距离输出点的距离控制着内插值受到已知点的影响，幂越高，则插值结果表现出越为平滑的效果。

3 插值结果分析

为了分析不同插值方法的准确性及误差大小，在实际的点位资料中选取部分点位作为参照值，对其进行插值并与实际数据对比，获得了不同参数、不同插值方法的插值云图（见图1），并通过误差分析图比较3种方法的插值精度。需要说明的是，由于输电线路基础勘察点位分布的特殊性，桩基选型和设计过程取决于输电线路上的岩土体力学参数，插值云图在输电线路周边范围可以保证一定的精度，但在周围没有数据的区域采用向两侧顺延的方式绘制。

用克里金插值法在进行不同的变异函数尝试后，发现球面半变异函数模型能够保证较好的精度，其余模型在对线性排列的点位进行插值时均会出现较大的误差，因此克里金法采用球面模型。从图1可以看出，由于数据主要集中在输电线路上，克里金法和反距离权重法得到的插值云图均为锯齿状，样条函数插值法得到的云图具有很好的光滑性。

3.1 承载力特征值的误差分析

图2 （a）～（c）分别给出了采用克里金、样条函数法和反距离权重法进行插值时承载力特征值的误差分析。图中点表示实际值，竖直向上的短线代表插值点出现大于实际值的偏差，竖直向下的短线代表插值点出现小于实际值的偏差，误差的大小由短线的长度来表示。

从插值结果上看，3种方法在对承载力特征值的插值过程中均保有良好的准确度，误差范围均控制在10%以内。在对承载力的插值中，样条函数的方法具有更强的稳定性。

3.2 内摩擦角的误差分析

图3给出了不同点位采用3种方法进行内摩擦角插值时的误差。和前文一样，竖直向上短线表示大于实际值，向下短线表示小于实际值。对比内摩擦角的误差图可以看出，克里金法对内摩擦角插值具有较好的插值精度，样条函数法在点位3处有较大的插值误差，接近11%，整体来说3种插值方法用于内摩擦角的插值时均能取得较好的效果。样条函数法受到带状分布点位的影响，在个别点位出现较大误差。

3.3 极限端阻力标准值误差分析

如图4所示，整体上，3种方法对极限端阻力标准值的插值精度基本相近，不同方法在个别点位上均有少许偏差。克里金法最大误差出现在第2个点，相对误差约6%;样条函数法在第3个点出现最大误差，最大相对误差约11%;反距离权重法在第6个点位出现最大误差，最大相对误差约7%;在其余点位处，3种方法均具有较好的插值精度。误差图中可以看出，3种插值方法均能保证一定的准确性，相对来说，样条函数方法在个别点位的误差较大。

4 幂参数对反距离权重插值结果的影响

从上述插值结果来看，样条函数法在面对条带状分布的数据时难以保证足够的精度，克里金法与反距离权重法插值精度比较接近。在实际选用时，由于反距离权重法逻辑简单，编程容易，本文选择采用反距离权重法进行插值。

在反距离权重法应用的过程中，其权重系数由式（2）确定，不同幂参数p时其权重系数也不一样。本小节以极限端阻力为例，分析不同幂参数对反距离权重法插值结果的影响。

如图5所示，随着幂参数的增大，各点位的影响范围也随之增大，远处点的影响越小。云图上来看，极限端阻力标准值的分布更有层次性。3次插值结果的数值整合如表 2所列。

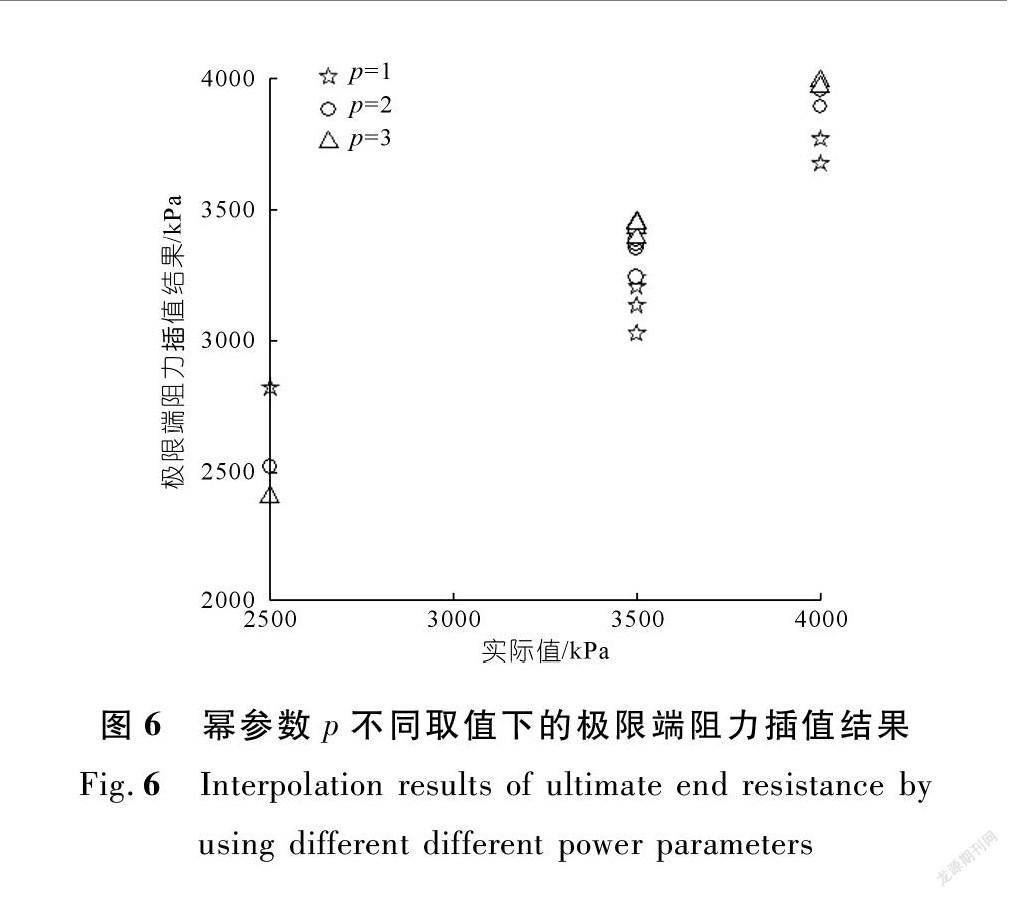
从图6可看出，随着幂参数p取值的增大，点位的分布更接近于45°线，即插值点的准确度越高。在不同的取值中，p=3时误差最小，精度最高。

5 结 论

采用克里金、样条函数和反距离权重法对输电线路上缺失的个别点位进行力学参数插值，从结果来看3种插值方法均能对承载力特征值、内摩擦角、极限端阻力进行合理估计，最大误差约10%左右。克里金法和反距离权重法插值精度相对较高。反距离权重法逻辑简单，编程容易，适用于输电线路桩基选型和设计的主要力学参数插值。

分析了反距离权重法用于插值极限端阻力时，不同幂参数对于插值精度的影响。发现幂参数从1增大到3的过程中，插值得到的极限端阻力云图变得更有层次性，插值精度也有一定程度的提高。

在输电线路地质情况和岩性特征无显著突变的情况下，本文中用到的插值方法可以用于输电线路桩基典型力学参数的插值。在满足现行勘察规范的前提下，设计部门可以依托ArcGIS等软件中的插值模块方便地对未勘察点位的主要力学参数进行合理估计，获得线路上更为详细的点位数据，方便设计人员进行桩基设计的优化和方案优选。

参考文献：

[1] 艾强.基于不同插值方法的地下水等值线图绘制研究[J].地下水，2012，34（3）：24-26.

[2] 秦俊桃，冯绍元，霍再林，等.几种地下水位空间插值方法在干旱内陆区的应用比较[J].中国农业大学学报，2010，15（5）：124-129.C6FDD2D9-7822-4550-B0C0-EBE1E13B2DD8

[3] 张灏，王娇，郑新奇.针对地质云钻孔数据的空间插值方法选择[J].矿山测量，2020，48（3）：12-16.

[4] 陈琳，任春颖，王宗明，等.基于克里金插值的耕地表层土壤有机质空间预测[J].干旱区研究，2017，34（4）：798-805.

[5] DAI K Y，LIU G R，LIM K M，et al.Comparison between the radial point interpolation and the Kriging interpolation used in meshfree methods[J].Computational Mechanics，2003，32（1-2）：60-70.

[6] LARGUECHE F Z B.Estimating soil contamination with Kriging interpolation method[J].American Journal of Applied Sciences，2006，3（6）：1894-1898.

[7] 张靖.基于克里金算法的点云数据插值研究[D].西安：长安大学，2014.

[8] 贺辰戋，欧阳婷萍，彭莎莎.广州市表层土壤磁学性质的空间插值方法比较[J].热带地理，2020，40（5）：903-918.

[9] 乔婷，姚彩燕，于东升，等，水田土壤有机碳时空演变下的最优插值方法[J].福建农林大学学报（自然科学版），2020，49（5）：683-694.

[10] 李增兵，趙庚星，赵倩倩，等.县域耕地地力评价中土壤养分空间插值方法的比较研究[J].中国农学通报，2012，28（20）：230-236.

[11] 杨成生，张勤，张双成，等.改进的Kriging算法用于GPS水汽插值研究[J].国土资源遥感，2013，25（1）：39-43.

[12] KRIGE D G.A statistical approach to some basic mine valuation problems on the Witwatersrand[J].Journal of the Southern African Institute of Mining and Metallurgy，1951，52（6）：119-139.

[13] 翟进乾.克里金（kriging）插值方法在煤层分布检测中的应用研究[D].太原：太原理工大学，2008.

[14] 张军.空间插值算法研究及其在遥感数据模拟中的应用[D].成都：成都理工大学，2013.

[15] 刘玲玲.耕地土壤养分空间插值与等级划分方法解析[D].合肥：安徽大学，2020.

[16] 李正泉，吴尧祥.顾及方向遮蔽性的反距离权重插值法[J].测绘学报，2015，44（1）：91-98.

（编辑：郑 毅）

Interpolation accuracy study on typical mechanical parameters of transmission

line pile foundations

SU Zhaohui1，DING Shijun2，CUI Qiang2，LIU Guang3，ZHANG Zhenhua3

（1.State Grid Corporation of China，Beijing 100031，China; 2.China Electric Power Research Institute，Beijing 102401，China; 3.School of Civil Engineering，Hefei University of Technology，Hefei 230009，China）

Abstract：

Transmission lines have characteristics of large span and wide distribution，which greatly increases the survey workload during the pile foundation construction of transmission lines.Based on some known transmission line survey data，we used Kriging，spline function and inverse distance weighting interpolation methods to make reasonable predictions on the main mechanical parameters at other sites of the same line.The interpolation errors of the three interpolation methods were compared in detail，and the main characteristics of different interpolation methods in interpolation of transmission line pile foundation parameters were analyzed.The results showed that the inverse distance weighting method was suitable for interpolating parameters of strip distribution，which had advantages of simple principle，easy programming，and good interpolation accuracy.More over，the influence of power parameters on interpolation of ultimate end resistance of foundations by the inverse distance weighting method was analyzed，and the results showed that the interpolation accuracy gradually improved when the power parameters increased.

Key words：

transmission line;survey of pile foundations;interpolation method;bearing capacity;internal friction angleC6FDD2D9-7822-4550-B0C0-EBE1E13B2DD8