Shapley值组合预测模型下的石狮市快递业务量预测分析

王凤英

（福建船政交通职业学院 交通经济系，福建 福州 350007）

近几年，国内电子商务的迅猛发展，催生了国内快递业务量的爆发式增长。截至2019年底国内已有七家快递企业上市，业务量呈几何倍数增长，而且中国快递进入到了“新百亿”时代。数量暴涨的同时部分地区仍然物流设施落后，配送效率低下，快递服务体验差，因此如何做到数量和质量双双提升对快递企业至关重要。如何合理规划网点的数量和配备合理的设施设备及人员对客户的服务提升是关键点，因此作为快递行业市场需求预测的重要指标，快递业务量的预测对快递企业的可持续发展非常重要。需求的定量预测模型常用的主要有回归分析预测法、时间序列预测法、神经网络预测法、灰色预测法等多种方法，但单一的预测模型的假设条件及使用范围总存在着一定的局限性，考虑因素比较单一，因此为了消除单一预测模型的缺陷，综合多种因素产生的影响，本文在综合三种预测方法的基础上，采用Shapley组合预测模型进行快递业务量的预测，提高模型预测的精度和稳定性，为快递行业的市场需求提供科学性支撑。

1 单项预测模型的选择与构建

1.1 多元回归预测模型的构建

快递业务量受到区域经济发展多种因素的影响，如区域经济的经济水平和规模、居民人均消费水平、社会固定资产投资总额，常住人口、社会消费品零售额等经济因素的影响。同时也会受到国家相关政策、信息处理技术及交通因素等非经济因素的影响。因此在构建预测模型时首先选用多元回归预测模型。回归预测模型的理论思想是选取合适的因变量，通过对大量的样本数据做回归分析，选取合适的数学模型和分析方法找出自变量和因变量之间的线性相关关系和数量关系。多元回归关系模型中的解释变量有多个，一般形式为：

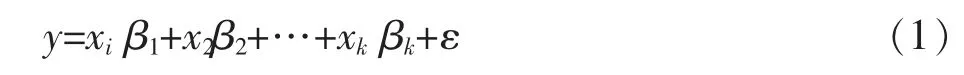
式中：y是被解释变量(因变量、相依变量、内生变量)，x是解释变量(自变量、独立变量、外生变量)，ε随机误差项，βi（i=1,2,…,n）是回归系数[1]。

回归预测模型在回归过程中利用初始变量可以采用向后回归、向前回归、逐步回归等多种预测方法对变量进行回归并进行检验，如果通过检验，则是满足了变量之间的模型假设，因此则可以利用此模型进行预测。

1.2 二次曲线估计模型构建

趋势曲线拟合模型主要是根据历史数据的特点选取直线或者各种曲线模型来进行拟合，然后根据选择的模型的拟合优度的大小来选取最优模型，目前常用的曲线估计模型有对数曲线、二次曲线、指数曲线、复合曲线和增长曲线等。快递业务量是一个时间序列，属于渐进变化，因此可选用二次曲线估计模型[2]。二次曲线估计预测模型建立如下：

本文综合考虑快递业务量的发展趋势采用二次曲线回归对其进行预测。

1.3 GM(1,1)灰色预测模型构建

灰色预测模型的预测原理是先对历史统计数据进行级比检验，如果没有通过此检验，将历史数据变化处理成能够通过级比检验的新数列，然后通过累加法、累减法或取初始值的方式进行灰生成，产生新的数据序列，然后建立微分方程代入求解，再将结果序列中的数据累减和逆变成即可得到目标预测值，最后进行误差检验、均方差检验等检验，评价预测效果。GM（1,1）模型是最常用的一种灰色预测模型。具体预测模型如下：

第一步，建立微分方程。

第二步，用最小二乘法估计参数a和u，构造矩阵B。

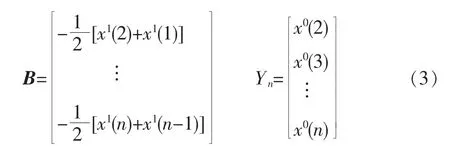
矩阵计算：

由该式进行矩阵运算可求的参数a，u。

第三步，求出预测模型。

将参数a和u代入时间函数得一次累加生成序列的预测模型：

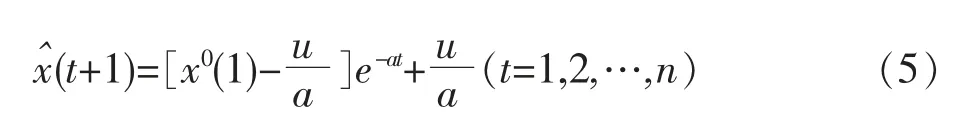
2 快递业务量的Shapley值组合预测模型构建

组合预测模型的计算公式为：

在组合预测模型中，权重的计算非常重要，合理的权重计算能够提高预测精度。选取Shapley值法来确定权重。Shapley值法是用于解决多人合作对策问题的一种数学方法，突出反映出各个成员在合作中的重要性，实现每个合作成员对该合作对策的贡献大小，易于被各个合作成员视为公平，结果易于被各方接受。假设有n种预测方法进行组合预测，记为I=｛1,2,…,n｝，对于I的任何子集，E(S)表示各组合的误差。设i种预测方法的预测误差的绝对均值为Ei，组合预测的总误差为E。

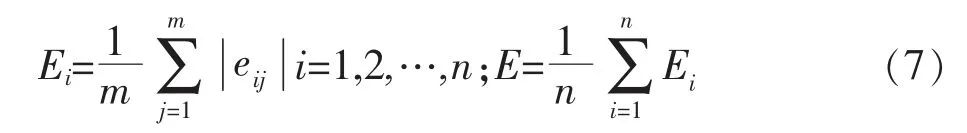
Shapley值误差分配公式为：

Shapley值法给出一个n人合作对策问题的分配向量，E（s）-E（s-{i}）表示组合s的边际贡献值，考虑组合成员加入后和加入前对组合产生不同的影响。可看作一个权重，表示组合成员在组合中所需要承担的边际贡献，也是组合预测的加权因子。Shapley值法综合了组织中各成员的影响，因此可认为其分配向量是公平合理的[4]。

由上可得权重计算公式

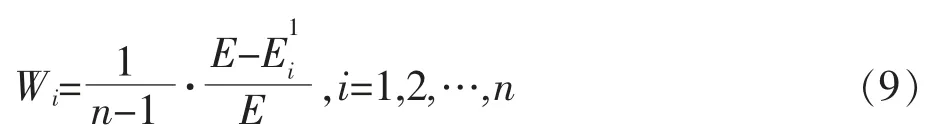
3 实证分析

3.1 石狮市快递业务的发展现状分析及数据选取

2018年，石狮市生产总值836亿元，增长9.1%，增速比上年提高0.6个百分点；工业增加值增长9.5%；综合经济实力位居全国中小城市百强第16位、福建省第2位。

在电子商务迅速发展的大背景下，随着GDP的逐年稳步提高，人民的消费水平大幅提高，石狮市的快递服务需求总量也随之持续增长，具体见图1。

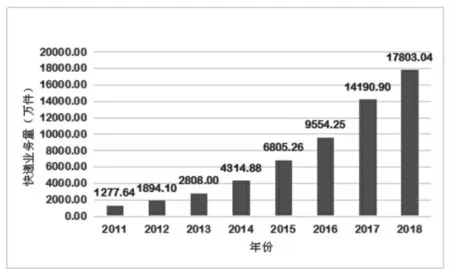
图1 石狮市历年快递业务量增长趋势图Fig.1 The growth trend of express delivery business in Shishi City over the years

3.2 多元回归关系模型预测

在对快递业务量的影响因素分析基础上本文选用了GDP、常住人口、社会消费品零售额作为快递业务量的解释变量。通过查阅石狮市的历年统计年鉴和公报具体数据见表1。选用SPSS 19.0对表1的数据进行多元回归分析。首先进行了相关性分析，快递业务量与这几个解释变量的相关性均在0.9以上，所以显著相关，然后选用向后回归进行分析，具体结果见表2。

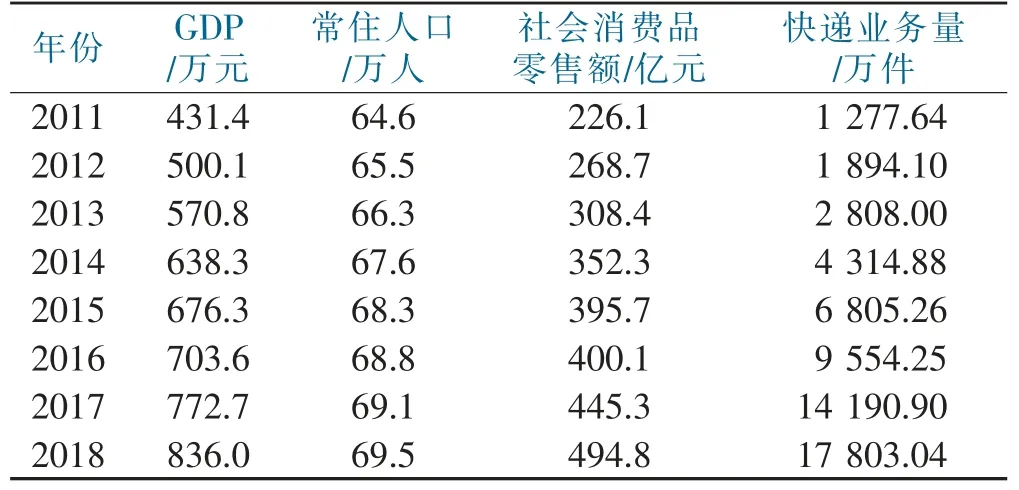
表1 2011—2018年石狮市快递业务量相关指标数据[5]Tab.1 Shishi city express business volume related index data in 2011 to 2018

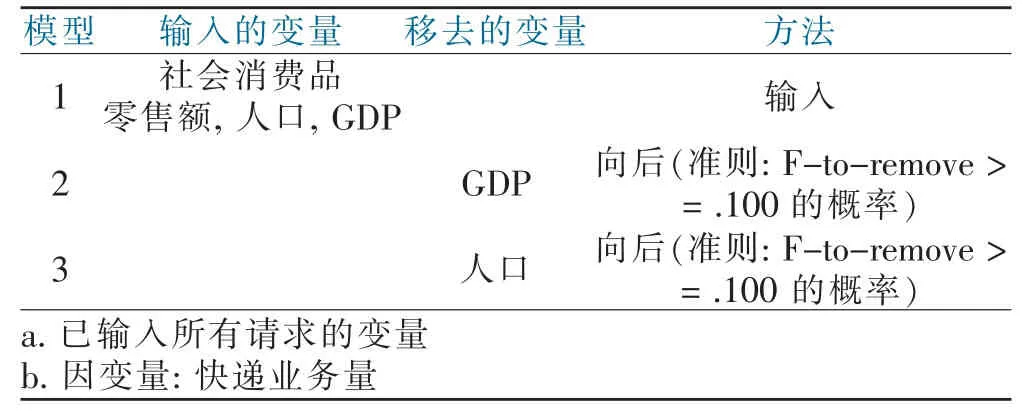
表2 输入/移去的变量Tab.2 Input/Removed Variables

由表2可以看出，向后回归过程中输入GDP、人口和社会消费品零售额三个变量，模型2移去变量GDP，模型3又移去变量人口，仅余下变量社会消费品零售额。并由表3的数据可以看出，模型3的t检验的显著性水平sig值均小于0.005，通过检验，因此多元回归方程为：快递业务量=-15 569.964+63.363×社会消费品零售额。

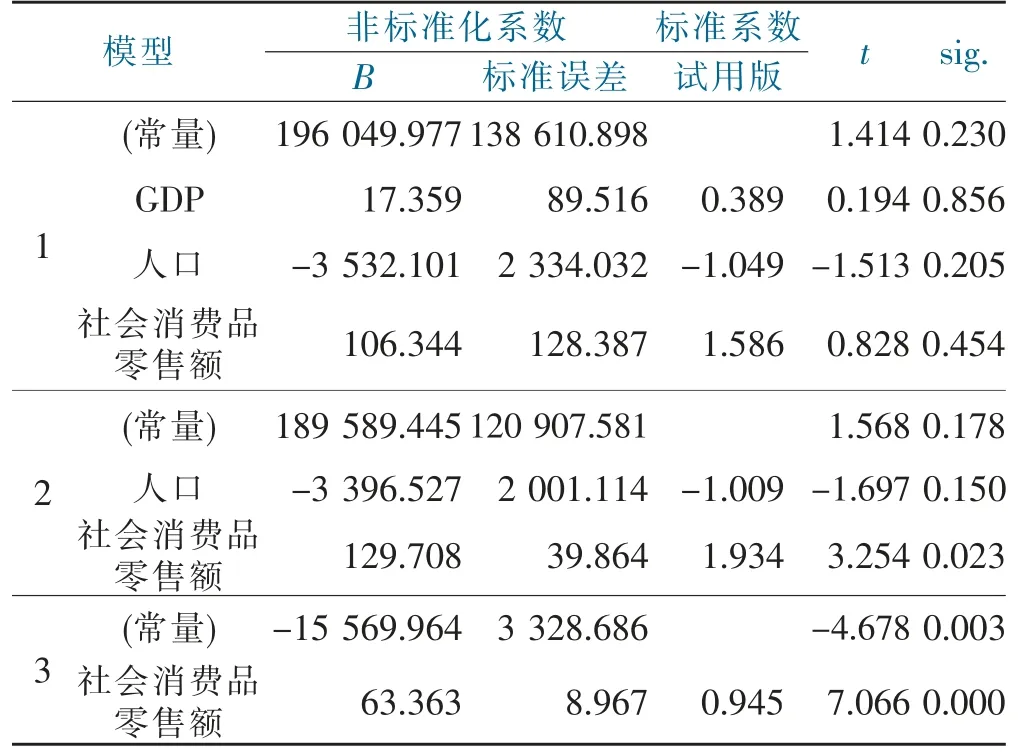
表3 系数aTab.3 Coefficient a

代入此回归方程计算出2011—2018年的快递业务量的预测值，见表4。

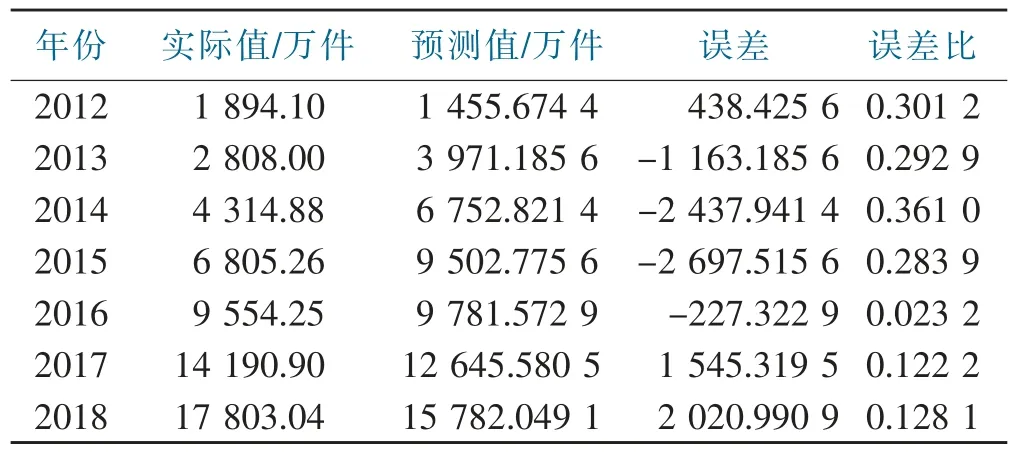
表4 多元线性回归模型预测值Tab.4 Predicted values of multiple linear regression models

根据表4可以计算出多元线性回归模型的平均绝对误差比为21.6%。

利用二次曲线估计回归模型对2019—2025年影响快递业务量的各指标进行预测，代入上述多元线性回归模型计算出快递业务量，结果见表5。

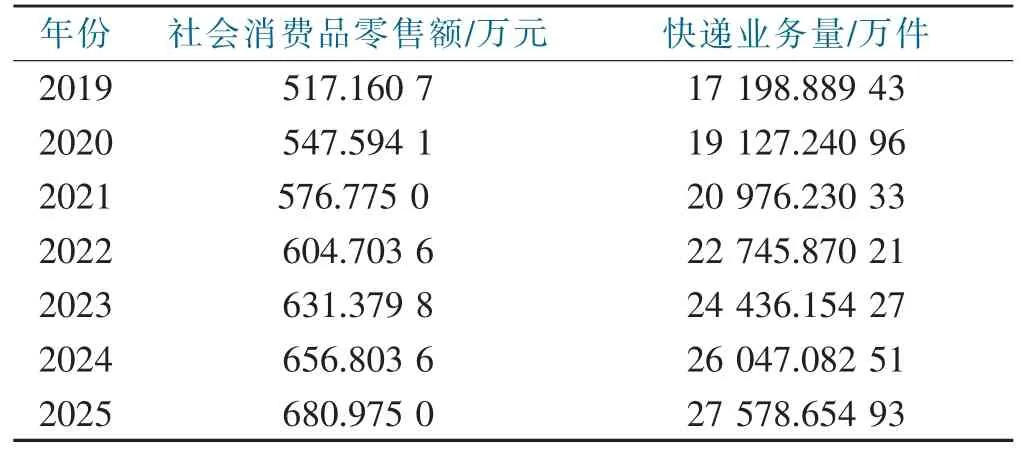
表5 2019—2025年石狮市快递业务量预测数据Tab.5 Shishi city express business volume forecast data in 2019 to 2025

3.3 二次曲线回归模型预测

选用SPSS 19.0软件对软件快递业务量的影响因素进行二次曲线估计回归。运行结果见表6。

表6 模型汇总和参数估计值Tab.6 Model summary and parameter estimates

由表6可知，该模型的R方等于0.998，说明模型的拟合度很高，显著性水平sig值为0.000，通过显著性检验。能较好地反应快递业务量的变化。同时由图2可知模型拟合效果很好。以年份为自变量X，以快递业务量为因变量Y，由表7可以得到二次曲线回归模型为：Y=1 708.487-671.898X+339.061X2

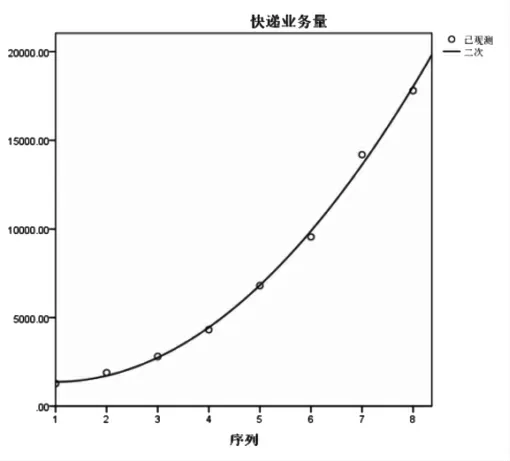
图2 二次曲线拟合图Fig.2 Quadratic curve fitting diagram

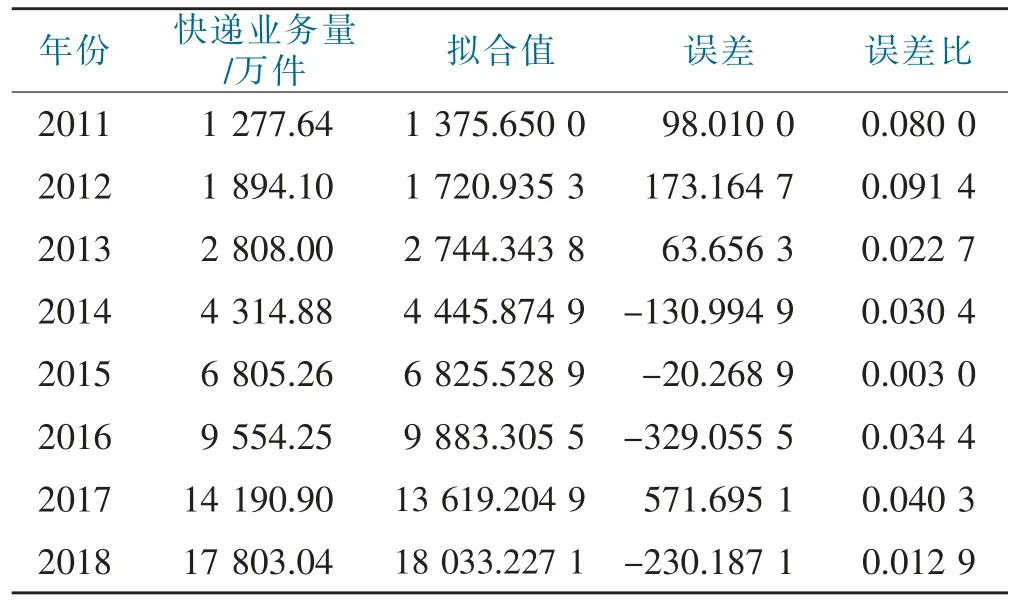
表7 二次曲线回归模型拟合值Tab.7 Quadratic curve regression model fitting values

利用二次曲线回归模型对2019—2025年进行预测得到结果如表8。

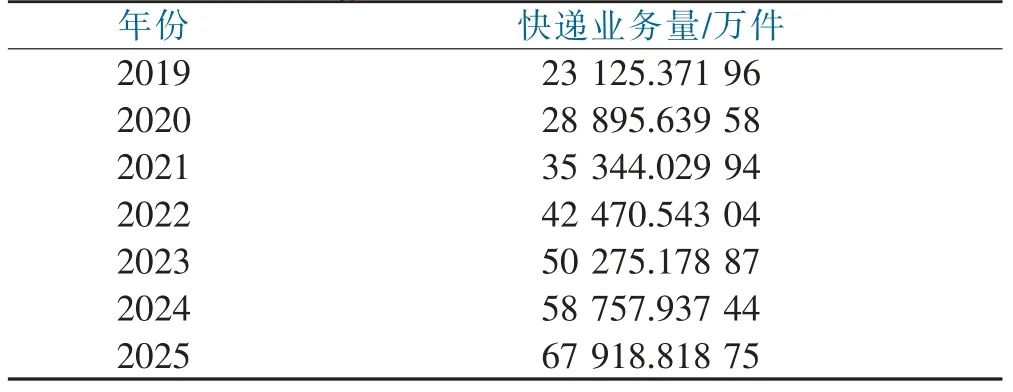
表8 2019—2025年二次曲线回归预测值Tab.8 The predicted value of the quadratic curve regression in 2019 to 2025

3.4 灰色预测方法

采用灰色预测分析软件，对原始数据进行模型GM(1,1)分析，计算过程如下：

第一步，原始序列的初始化。

初始化后的序列：

1 277.64,1 894.10,2 808.00,4 314.88,6 805.26,9 554.25,14 190.90,17 803.04

第二步，原始序列的1-AGO。1-AGO序列：

1 277.640 0,3 171.740 0,5 979.740 0,10 294.620 0,17 099.880 0,26 654.130 0,40 845.030 0,58 648.07

第三步，1-AGO的紧邻均值生成。紧邻均值生成序列：

2 224.690 0,4 575.740 0,8 137.180 0,13 697.250 0,21 877.005 0,33 749.580 0,49 746.550 0

第四步，发展系数和灰色作用量的计算：

a=-0.343 6 b=1 618.673 0。

第五步，模拟值的计算：

1 277.640 0,2 455.283 3,3 461.844 9,4 881.053 8,6 882.077 9,9 703.436 7,13 681.432 4,19 290.236 9

第六步，计算残差：

残差=3 562 462.047 9。

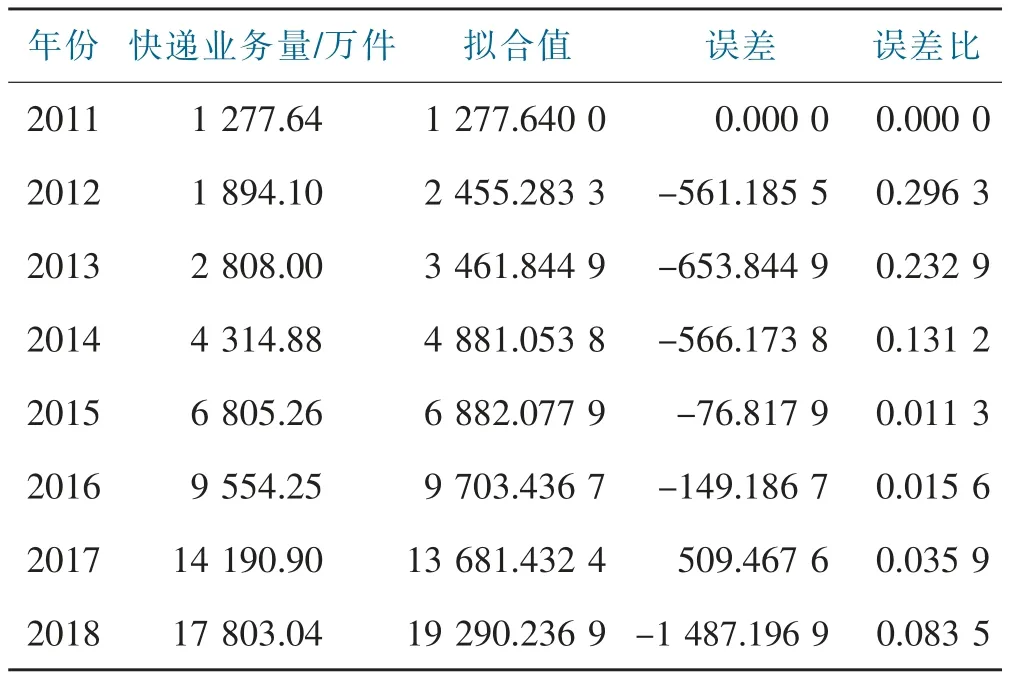
表9 GM(1,1)模型预测误差分析Tab.9 GM(1,1)model prediction error analysis

利用灰色预测方法对2019—2025年进行预测结果见表10。

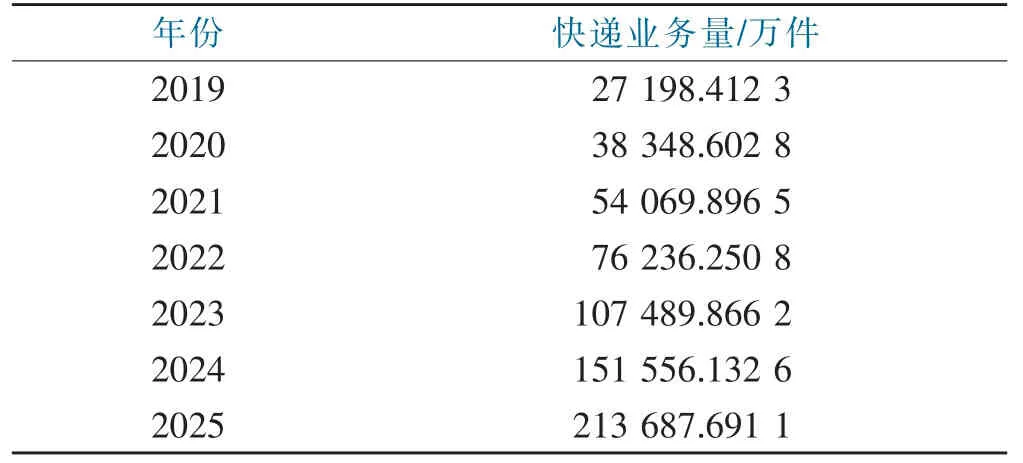
表10 灰色预测方法的预测值Tab.10 Predicted values of gray prediction method

3.5 Shapley组合预测模型

根据上述三种方法的预测结果，用Y1，Y2，Y3，分别代表多项回归预测模型、二次曲线估计预测模型和灰色预测模型，选取2012—2018年石狮市快递业务量的历史数据为样本，由上述表4，表7和表9计算出Shalpey组合预测的总误差比为

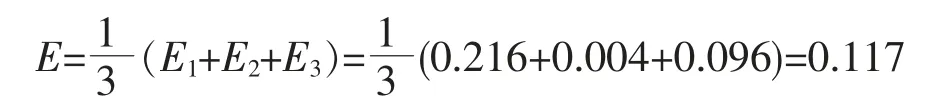
根据Shalpey值组合预测的概念，三种预测方式的所有子集的组合的误差比分别为E{1}，E{2}，E{3}，E{1,3}，E{2,3}，E{1,2,3}，通过计算公式其数值的大小为该子集所包括的向量误差比的均值大小结果见表11。

表11 各子集的误差比值Tab.11 Error ratio of each subset

按照Shapley值误差分配公式，分别求出三种预测方法的Shapley值为：

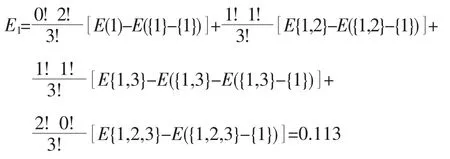
同理可计算出E2=-0.019,E3=0.023，三个结果和为E1+E2+E3=0.117，说明三种单一预测方法分摊的误差比的和等于总的误差比。根据计算公式wi=计算出三种预测方法在组合模型中的最终权重为0.017，0.581，0.402。根据所得的权重，可得组合预测模型为，利用组合预测模型公式可以得到石狮市快递需求量组合预测结果见表12。

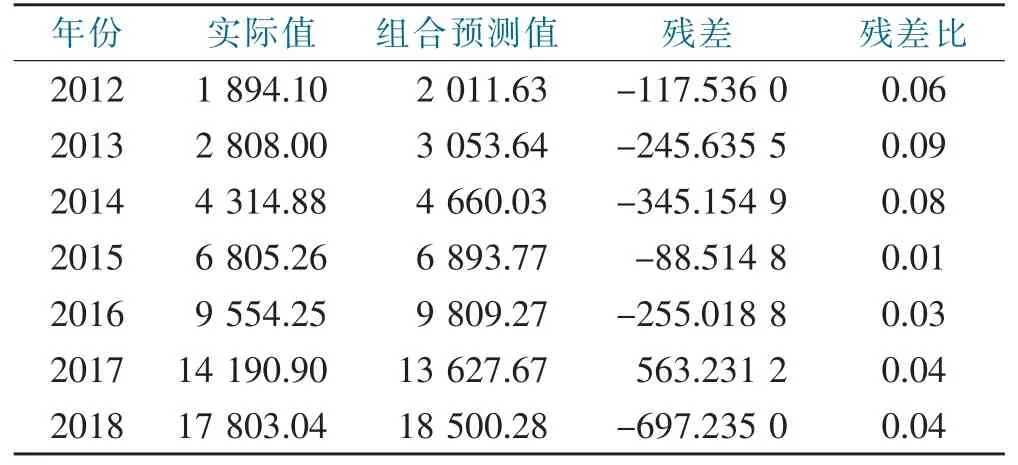
表12 2012—2018年组合预测结果Tab.12 Combined forecast results in 2012 to 2018

根据表11计算出组合预测的平均误差比5.00%，预测精度良好。

将表13的三种单一预测结果代入组合预测模型，由此可得2019—2025年组合预测值，见表13的最后一列。

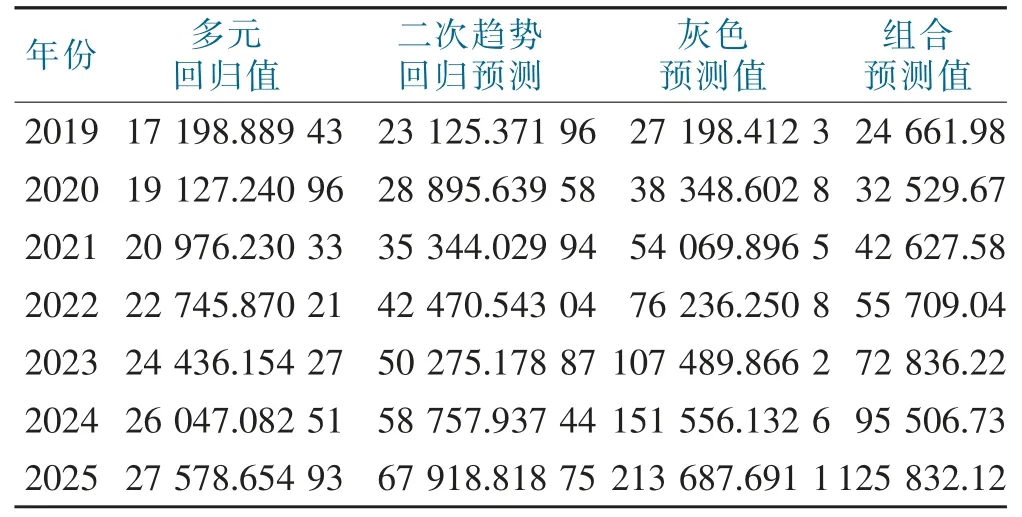
表13 2019—2025年各模型预测结果汇总Tab.13 Summary of the prediction results of each model in 2019 to 2025

四、结束语

在快递业务量的需求预测中，单个预测方法存在一定的局限性，在选择多元线性回归、二次曲线回归、灰色预测方法的基础上，利用Shapley组合预测方法进行预测，综合多种因素，提高预测的全面性。以福建省石狮市快递业务为例，证明组合预测方法的有效性，进而对区域的物流网络规划提供了一定的指导意义，为电子商务及区域经济的发展贡献力量。