基于网络结构和信息传播的节点重要性识别方法

赵宇臣， 郭进利

(上海理工大学 管理学院， 上海 200093)

随着科学信息技术的高速发展，复杂网络理论已经在人类社会中各个复杂系统取得巨大研究进展，人类的日常生活也越来越依靠复杂网络系统的稳定性[1]。复杂网络的不同节点在网络中承担功能不尽相同，其中网络中某些重要节点对网络结构有较大影响，甚至对网络结构的稳定性和鲁棒性起到决定性作用[2]。所以对网络重要节点的挖掘和排序不仅具有重要的理论价值，还具有显著的实践价值，如网络中社区发现、病毒疾病发现与控制等。

近些年来，关于如何对复杂网络中的重要节点进行识别和排序，目前国内外研究人员发展了很多方法，根据特点不同可以将其分为以下4类：

1)基于邻居节点的排序方法。根据节点本身拓扑结构性质的度中心性(degree centrality， DC)进行排序是一种简单有效的局部排序算法[3]；根据节点中心性的H指数(H-index centrality，H)进行排序以及将网络进行分解通过节点的K核分解中心性进行排序(K-Shell decomposition centrality，KS)[4]。

2)基于路径的排序方法。根据一个节点位于其他节点最短路径上的介数中心性(betweenness centrality，BC)进行排序[5]；根据一个节点到其他节点距离之和的倒数的紧密中心(closeness centrality，CC)进行排序[6]。

3)基于特征向量的排序方法。根据一个节点的邻居节点的数量和重要性，即节点的特征向量中心性(eigenvector centrality，EC)[7]进行排序。

4)基于节点删除和收缩的排序方法。通过判断删除网络中某个节点后对网络结构和功能的负向影响，从而反映节点对于网络的重要程度。(复杂网络中节点重要度评估的节点收缩方法)。

上述的节点重要性评价指标主要是基于节点自身性质来判断的，且判断的维度较为单一，无法普适于各种类型的网络之中。基于此，国内学者综合考虑这些因素，根据具体的研究背景，对现有的节点重要性评价标准进行改进。Gao等根据节点及其邻居节点的性质，通过判断节点局部结构中心性进行排序[8]；Kitsak等通过分析传播动力学中网络SIR模型，根据节点在网络中的传播效率判断节点的重要程度[9]；Wei等利用马尔科夫链分析节点在网络中的动态性质，判断节点在网络中的重要程度[10]。还有学者将多属性决策理论应用在网络节点重要性的判断中。Yang等利用Topsis方法，综合评价单一指标的权重，提升节点重要性判断的准确性[11]；Lin等通过D-S方法综合考虑多个中心性指标，提出了一种全新赋值的方法，判断节点的影响力大小[12]。近些年来，许多学者提出基于邻居节点的结构特征的节点重要性排序算法。Gao等通过分析节点邻域节点的联通子图数，判断节点的影响力[13]；Bea等通过节点及其邻节点的重要性，进行过节点的网络边缘度值分析，判断节点重要性[14]；Zareie等通过分析邻节点结构特征的多样性，大大提升了节点重要度排序的准确性[15]；Wang等利用网络中节点与邻居节点的壳值，提出了多阶邻居壳数向量中心性算法，表示节点的重要性[16]。

目前基于网络局部信息的节点重要性评估主要是针对节点的本身属性研究的，未充分考虑邻居节点的结构特征对节点重要性的影响。且现实生活中的大规模网络结构会随时间的迁移而变化，获取完整结果网络结构数据信息较为困难。因此通过全局网络结构信息定义节点的影响力具有一定的局限性。本文通过量化网络局部信息，基于网络节点及其邻节点的拓扑结构特征，提出一种新的网络节点重要性评估算法LSC。并在4个实际网络和两个人工网络中进行实验验证，证明此算法能更加准确地评估节点的重要性。

1 算法改进

(1)

Salotn指标与Jaccard指标相比优势在于，当处理节点的共同邻域时，Jaccard指标没有考虑到每个共同邻域节点在量化过程中计算权值是不一样的，但在实际网络中，不同节点的权值会对网络重要节点的评价产生误差。所以在此基础上，引入Salotn系数作为判断网络邻域节点的相似性指标更加合理。

首先，在实际网络中节点的邻域节点数量越多，且邻域节点间的拓扑结构重合性越小，表明邻域节点的相似性越低，节点对于邻域节点的影响力越大，对整个网络来说更加重要。基于以上分析，提出一种基于节点本身度数和邻域节点相似性的节点重要性评价算法LSC(i)，表示为

(2)

(3)

其次，利用信息传播相关理论对LSC算法进行修正，当节点i的LSC值大于0时，节点i和其邻节点j之间的信息传播才有意义，故保留其LSC值；当LSC值小于或等于0时，LSC取0值。例如在SIR模型中，当传播值大于两节点之间的阈值时，才可以进行传播；当传播值小于或等于两节点之间的阈值时，不进行传播。基于这点增加了f(X)函数对LSC算法进行修正来保证算法的准确性，计算公式为

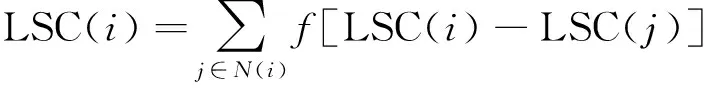
(4)

(5)

综上分析，算法LSC综合考虑了节点本身度数和邻居节点的拓扑结构，并利用信息传播对节点的LSC值进行修正，当节点i的LSC值越大时，i的度数越大且与其邻居节点相似性越小，即与邻节点的拓扑结构重合性越小，说明节点i对网络的重要性越高；反之，当节点i的LSC值越小时，对网络的重要性越低。可以利用节点的LSC值的大小对网络中节点的重要性进行判断。

2 评价标准

为验证算法的可行性，本文采用3种方法对节点重要性排序的算法进行度量。

2.1 网络效率法[18-19]

通过移除利用算法识别出的重要节点，模仿对网络中重要节点进行蓄意攻击，比较移除节点前后对网络效率的影响。网络效率可以用来评价网络的联通性，当某些节点及其连接边被移除时，使得其他节点间最短路径变大，进而影响整个网络的平均路径长度。当网络效率变化越大，说明节点越重要；反之，说明节点越不重要。网络效率可以表示为

(6)

(7)

2.2 极大联通系数法[20]

按照节点重要度评价指标，将节点按重要度从大到小进行排序。移除一部分节点后，观察对网络极大连通子集的影响，计算公式为

G=R/N

(8)

式中：R表示移除一部分节点后的网络极大连通子集的节点数；N表示网络中节点总数。极大连通子集规模随着节点移除而变小的趋势越明显, 表明采用该方式攻击网络节点的效果越好，识别出的节点对于网络的重要性越高。

2.3 单调性

节点单调性是区分节点传播能力和等级的重要指标之一，反映了在某指标下节点的得分情况，单调性指标值越大，节点获得相同得分的数量越少，算法的效果就越好，计算公式为

(9)

式中：n表示序列R中的节点数量；nr表示在等级r上的节点数量；M的取值范围为[0，1]，其数值较大表示该方法具有较高的评估准确率。

3 实验数据收集

考虑到不同网络具有不同的拓扑结构，本文共使用4个真实网络数据集和2个人工网络数据集进行仿真实验。真实网络包括karate美国空手道俱乐部、Dolphins海豚网络、Adjnoun美国空军局域网络和Celegansneural网络；人工网络包括WS小世界网络(WS)和BA无标度网络，人工网络均通过Python软件自动生成，其中BA的参数为N=500,M=5，WS的参数为N=500，K=5，P=0.5[21-22]。4个真实网络和2个人工网络的拓扑特性见表1。

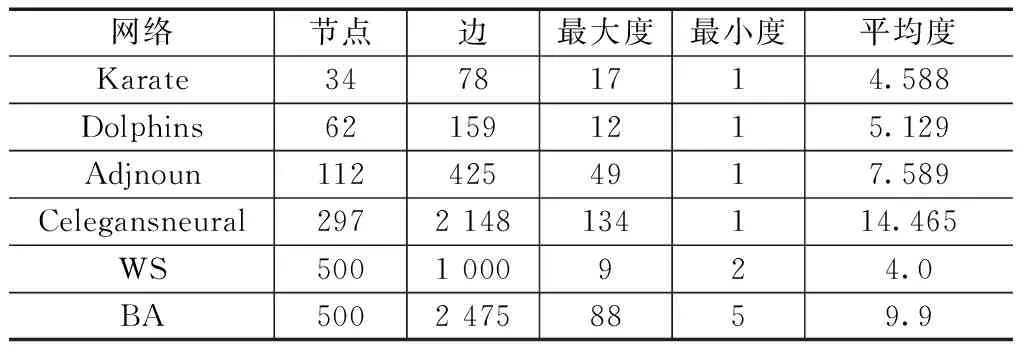
表1 4个真实网络和2个人工网络的拓扑特性

4 实验结果分析

为评价本文提出重要性节点评价算法LSC的性能，进行以下实验：①以蓄意攻击的方法移除一定比例P排名靠前的节点，模拟网络遭受蓄意攻击的极大连通子图规模和网络效率的变化，从而评价各个节点重要性排序的方法；②将LSC算法与基于局部相似性的LLS算法、基于节点位置信息的K-shell算法、Local Centrality算法和同样采用局域信息的度的排序Degree算法进行单调性分析与比较，利用单调性检验不同中心性序列对于节点重要性的区分能力。

4.1 蓄意攻击效果

在蓄意攻击网络结构对网络极大连通系数G影响的实验中，通过采用K-shell指标、LC指标、Degree指标、LLS指标和本文提出的LSC指标对6个真实网络和2个人工网络中排名靠前的节点进行移除，对网络影响结果如图1所示。在所有的8个网络中，从实验结果的整体趋势来看，LSC指标导致网络的极大连通系数变小的走势最为明显，且LSC指标总是以最少的移除节点比例就能最先使网络的极大连通系数降到最低，说明综合考虑网络局部拓扑结构相似性和信息传播理论的网络节点识别算法(LSC)能更好地识别出关键节点。尤其在实际网络[图1(b)]和人工网络[图1(e)]中表现得更为明显，LSC指标在蓄意攻击过程中对网络极大连通影响明显优于其他算法指标。比较LSC指标和LLS指标，从6个网络实验结果来看，当移除相同比例的节点时，在多数情况下LSC指标可以使网络的连通性下降更大的幅度，说明LSC指标通过对算法的优化，相比于LLS指标在网络重要节点识别的准确性上有较大的提升。

图1 利用不同指标攻击网络重要节点后极大连通系数的变化

本文采用网络效率比较K指标、LC指标、D指标、LLS指标和本文提出的LSC指标的性能。利用上述的节点重要性评价指标删除一定比例排序靠前的节点，网络效率下降率μ随着网络连通性的变化而变化，连通性越差网络效率的下降趋势越明显。图2反映了不同节点重要性指标下删除一定比例节点后，网络效率的变化情况。由图2可知，随着网络节点移除比例的增加，LSC指标导致网络效率下降的幅度最为显著，明显优于其他指标。特别是在图2(d)Karate网络中，从移除节点开始网络效率下降的幅度高于其他指标，一直保持到网络效率下降到0，且随着移除节点的增加网络效率下降趋势并没有出现负向波动，说明通过LSC算法识别的关键节点更加准确。

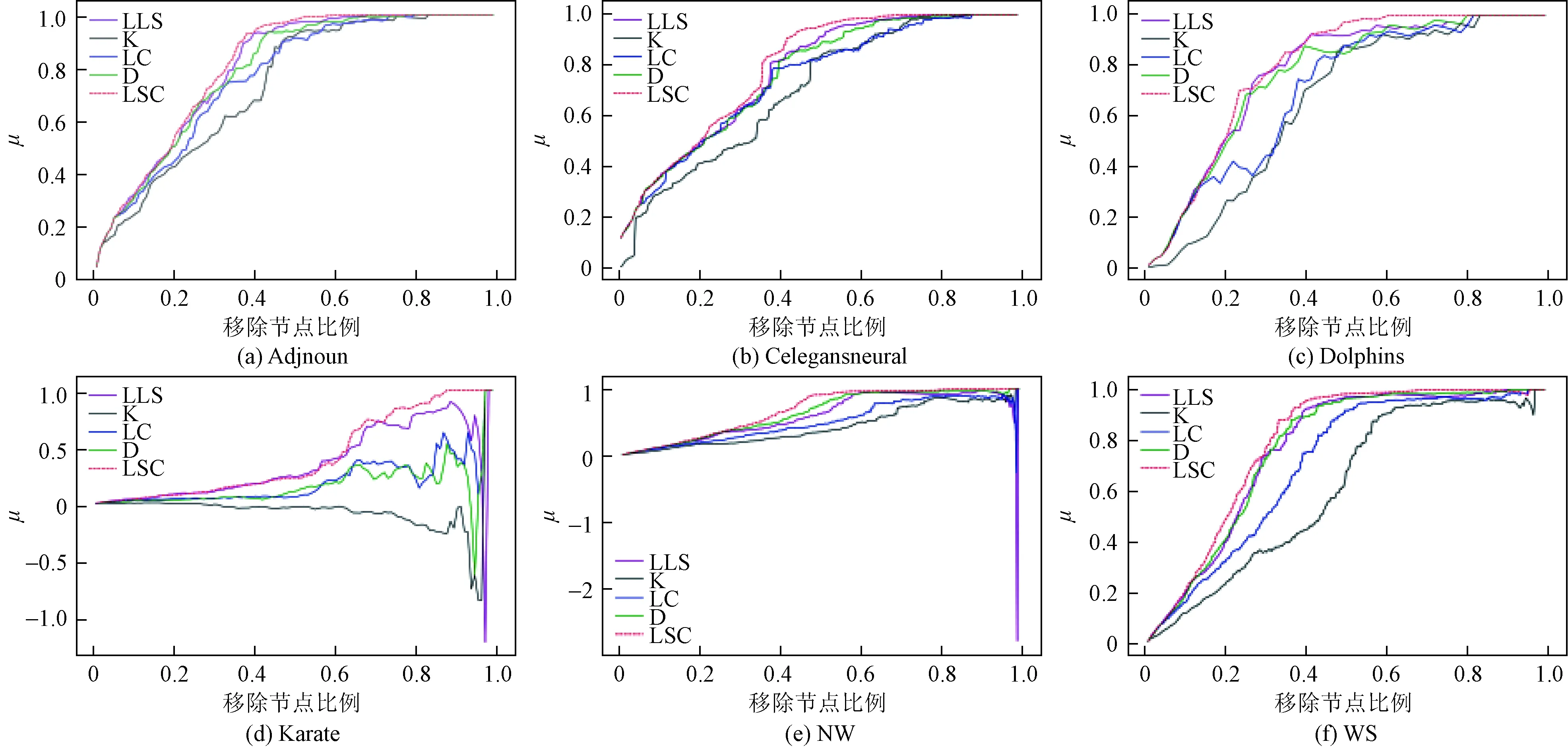
图2 利用不同指标攻击网络重要节点后网络效率的变化

综上所述，利用LSC算法的节点排序方法破坏网络拓扑结构时，网络效率和网络的极大连通系数变化得最为显著，说明LSC算法可以更加准确地识别出网络中的重要节点。

4.2 单调性

不同指标在各网络中得到网络节点单调性值见表2。表2结果表明，LSC算法除了在Karate网络中关键节点的单调性LC算法和Degree算法外，在其他网络中单调性均高于其他4种算法，单调性反映了在某指标下节点的得分情况，单调性指标值越大，节点重要性排序有较好的差异性，算法的效果就越好。与LLS算法相比，LSC算法在4个真实网络中的重要节点的单调性数据均优于LLS算法，说明可以更加准确地评估节点的重要度。

表2 不同指标在不同网络数据上的单调性值

5 结语

复杂网络关键节点的准确识别具有重要的理论意义和实践价值，不仅对加快有益信息在网络中的传播、抑制病毒的爆发具有现实意义，还有助于提

升网络的抗毁性和稳定性。在已有研究的基础上，本文综合考虑节点度以及邻居节点的结构相似性，利用信息传播的性质对算法进行修正，提出了基于网络节点结构和信息传播的复杂网络节点识别的新方法，并在4个真实网络和2个人工网络中进行仿真实验，验证算法的可行性。实验表明LSC指标在网络连通性、网络效率及节点的单调性3个方面均优于其他比较算法，说明LSC算法可以更好地识别出网络中的重要节点。同时也希望为后续的研究提供一定的参考。本研究所用的网络均为无向无权网络，如何将此方法应用于有向加权网络以及据时态变化的网络是后续的研究重点。