环F2[u]/(ue+1)上一类常循环LCD码及其Gray象
黄 山
(安徽警官职业学院 信息管理系,合肥 230031)
0 引 言
LCD码在数据存储和对称密码中有重要应用。1964年,Massey引入有限域上的可逆码,将其应用于解决数据的有效存储。[1]1992年,Massey正式提出LCD码的概念[2],并在文献[3]中研究了循环LCD码。2015年,Carlet等将LCD码应用于抵抗侧信道攻击和错误注入攻击。[4]此后,有限域上的LCD码得到广泛的研究。[5,6]2018年,Carlet等人[7]证明,给定有限域Fq上参数为[n,k,d]的线性码,当q>3时,Fq上存在一个与其等价的LCD码。自此,有限域F2上的LCD码成为重点研究对象。
2017年,Rao等[8]研究了F2上奇数长度n≤257的LCD循环码,得到了一些参数好的LCD码。2018年,Galvez等人[9]研究了F2上维数k=2的LCD码的码长上界。2019年,Harada等[10]研究了F2上小维数的LCD码的码长上界。同年,Fu等[11]利用矩阵的方法,讨论了F2上LCD码的存在性;Zhou等[12]利用矩阵方法,给出了一种构造F2上LCD码的方法,并构造了参数优的LCD码。2020年,Huang等人[13]引入绝对陪集首的概念,构造了几类F2上LCD BCH码;Wu等人[14]通过单复形构造了F2上参数优的LCD码。2021年,Araya等人[15]研究了F2上维数k=5的LCD码的最大极小重量;Harada[16]通过调整已知自对偶码的构造方法,构造了F2上参数好的LCD码;最近,Bouyuklieva研究了F2上LCD码的截断和打孔码,对于给定的码长和维数,给出了LCD码的最小距离的上界。[17]
2015年,Liu等人[18]给出了有限链环上线性码是LCD码的必要条件,在一定条件下,给出了有限链环上线性码是LCD码的充分条件。2019年,Shi等人[19]研究了长度为2n的双循环4码。同年,Liu等人[20]利用有限交换环上的线性代数理论,给出了有限交换环上线性码是LCD码的若干判定准则;Bhowmick等人[21]证明有限交换Frobenius局部环上不存在非自由LCD码,并利用MAGMA软件,得到了环4上一些新的最优循环LCD码。最近,廖等人[22]研究了环4上偶长度的负循环LCD码,构造了一类最小Lee距离至少是6的LCD码;开晓山等人[23]研究了环4上奇长度的循环LCD码,构造了4上长度为2m+1的循环LCD码,得到了参数好的二元非线性可逆码。
本文将研究环F2[u]/(ue+1)上任意长度的(1+λu)-常循环LCD码的代数结构及其Gray象,其中λ是环F2[u]/(ue+1)的单位。易知,环F2[u]/(ue+1)是一个有限链环。Norton等人[24]给出了有限链环上线性码的代数结构,并在文献[25]中证明有限链环上线性码的Hamming距离等于其最高阶挠码的Hamming距离。Cao在文献[26]中给出了有限链环R上任意长度的(1+λγ)-常循环码及其对偶码的代数结构,其中λ是环R的单位,γ是环R的极大理想的生成元。下文通过引入一个恰当的Gray映射,利用环F2[u]/(ue+1)上(1+λu)-常循环LCD码的Gray象,构造F2上的LCD码。
1 预备知识
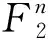
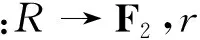
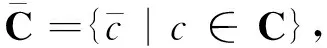
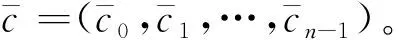
在Rn上,n-元组a=(a0,a1,…,an-1)和b=(b0,b1,…,bn-1)的内积定义为
a·b=a0b0+a1b1+…+an-1bn-1。
环R上长度为n的线性码C的对偶码,记作C⊥,定义为{b∈Rn|a·b=0,∀a∈C}。由文献[24],|C|·|C⊥|=|R|n。如果C∩C⊥={0},则称C是环R上长度为n的LCD码。文献[21]证明,环R上的LCD码都是自由码。
设λ∈R是一个单位,则1+λu也是环R的单位。设C是环R上长度为n的线性码,如果对任意的(c0,c1,…,cn-1)∈C,((1+λu)cn-1,c0,…,cn-2)∈C,则称C是环R上长度为n的(1+λu)-常循环码。由文献[26],C⊥是环R上长度为n的(1+λu)-1-常循环码,其中(1+λu)-1表示1+λu的逆元。定义
σ:Rn→R[x]/(xn-1-λu)
(c0,c1,…,cn-1)c0+c1x+…+cn-1xn-1
且σ(C)={σ(c)|c∈C}。则C是环R上长度为n的(1+λu)-常循环码当且仅当σ(C)是商环R[x]/(xn-1-λu)的理想。在不引起混淆的情况下,本文不区分C和σ(C)。设
f(x)=1+f1x+…+ftxt+xt+1∈F2[x]
其中t≥-1是整数。f(x)的互反多项式定义为f*(x)=1+ftx+…+f0xt+xt+1。当f*(x)=f(x)时,f(x)称为自互反多项式。设n=2s,其中s为非负整数且为正奇数。x-1在F2[x]上唯一分解为不同的首一不可约多项式的乘积,即
(1)
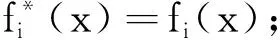
引理1[26]设x-1在F2上的因式分解如式(1)。设C是环R上长度为n的(1+λu)-常循环码,则存在0≤ai,bi,ci≤2s(e+1)使得C的生成多项式
(2)
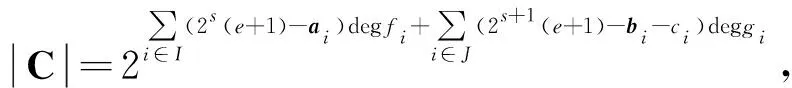
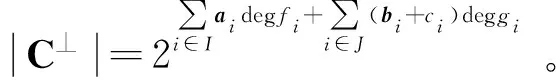
2 主要结果
下面,给出环R上任意长度的(1+λu)-常循环LCD码的代数结构。
定理1 设C是环R上长度为2s生成多项式为式(2)的(1+λu)-常循环码,则C是环R上长度为2s的LCD码当且仅当,对任意i∈I,ai=0或2s(e+1)且对任意i∈J,bi=ci=0或2s(e+1)。
证明必要性 由引理1,
容易验证,c(x)=0当且仅当,对任意i∈I,max{ai,2s(e+1)-ai}=2s(e+1);对任意i∈J,
max{bi,2s(e+1)-ci}=max{ci,2s(e+1)-bi}=2s(e+1)
由此推出,对任意i∈I,ai=0或2s(e+1);对任意i∈J,bi=ci=0或2s(e+1)。
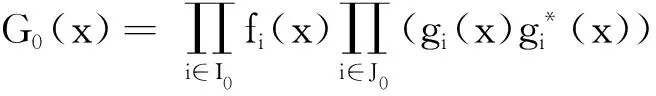
假设存在c(x)∈R[x]使得c(x)∈C∩C⊥且c(x)≠0,则存在a(x),b(x)∈R[x]使得
c(x)=a(x)g(x)=b(x)g⊥(x)
h(x)g(x)+l(x)g⊥(x)=1
于是,在R[x]上,
b(x)=b(x)[h(x)g(x)+l(x)g⊥(x)]=
h(x)b(x)g(x)+l(x)a(x)g(x)=
[h(x)b(x)+l(x)a(x)]g(x)
因此,在R[x]/(x2s-1-λu)上,
c(x)=b(x)g⊥(x)=[h(x)b(x)+l(x)a(x)]g(x)g⊥(x)=0
这与c(x)≠0矛盾。
由定理1,环R上(1+λu)-常循环码是LCD码有如下等价的判定定理。
定理2 设C是环R上长度为2s生成多项式为g(x)的(1+λu)-常循环码,则C是LCD码当且仅当存在x-1在F2[x]上的自互反因式f(x)使得g(x)=f(x)2s(e+1)。
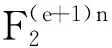
r=r0+ur1+…+uere


2010年央行宣布重启人民币汇率形成机制改革后,人民币汇率继续升值,但由于此时我国新增4万亿经济刺激计划的逐步落实,宏观经济增长率并没有出现大幅下滑,但此次经济增长更多依赖于国内投资和内需增加,并引发国内物价的小幅上升;此外,在全球货币贬值背景下人民币币值的坚挺也使我国进出口贸易受到影响。由于后金融危机时期我国经济对世界经济的带动地位,我国外汇储备规模得到了进一步提升。
dG(C)=min{dG(a,b)|a,b∈C,a≠b}
如果C的Gray距离为dG,则称C是环R上(n,M,dG)线性码。C的Gray象定义为
ΦA(C)={ΦA(a)|a∈C}。
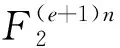
证明由映射ΦA的定义,对任意a=(a0,a1,…,an-1),b=(b0,b1,…,bn-1)∈Rn,
注意到,对任意a,b∈F2,φA(a-b)=φA(a)-φA(b),则
容易验证,对任意a,b∈Rn,ΦA(a-b)=ΦA(a)-ΦA(b)。由引理2,如下性质成立。
定理3 设C是环R上(n,M,dG)线性码,则ΦA(C)是F2上[(e+1)n,log2M,dG]线性码。
为了确定ΦA(C)的对偶码的代数结构,设J是F2上斜对角线及其以上元素全为1其余元素均为0的e+1阶方阵,即
我们有如下结论。
定理4 设C是环R上长度为n的线性码,则ΦA(C)的对偶码ΦA(C)⊥=ΦJ(A-1)T(C⊥),其中A-1表示A的逆矩阵,AT表示A的转置矩阵。
证明设a∈ΦJ(A-1)T(C⊥),则存在b=(b0,b1,…,bn-1)∈C⊥使得
a=(φJ(A-1)T(b0)‖φJ(A-1)T(b1)‖…‖φJ(A-1)T(bn-1))。
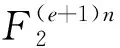
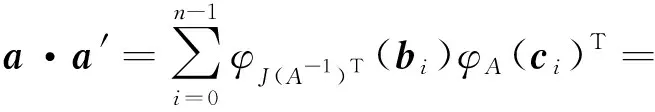
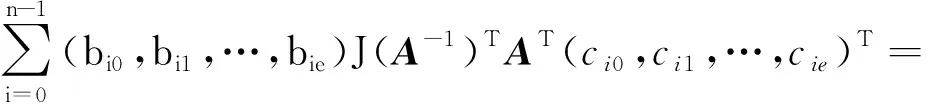
其中bi=bi0+ubi1+…+uebie,ci=ci0+uci1+…+uecie。在Rn上,
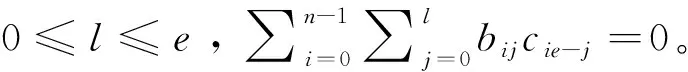
ΦJ(A-1)T(C⊥)⊆ΦA(C)⊥
另一方面,|ΦJ(A-1)T(C⊥)|·|ΦA(C)|=|C⊥|·|C|=|R|n=2(e+1)n,即|ΦJ(A-1)T(C⊥)|=|ΦA(C)⊥|。所以,
ΦA(C)⊥=ΦJ(A-1)T(C⊥)。
引理3对任意正整数e,在F2上存在e+1阶方阵A使得AAT=B。
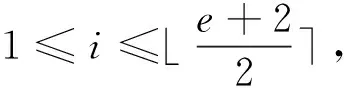
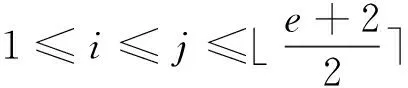
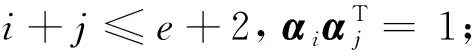
结合定理4,如下结论成立。
定理5设A是F2上e+1阶方阵且AAT=B。设C是环R上长度为n的线性码,则ΦA(C)是F2上长度为(e+1)n的LCD码当且仅当C是环R上长度为n的LCD码。
证明注意到A=B(AT)-1,由定理4,ΦA(C)⊥=ΦA(C⊥)。因此,
ΦA(C)∩ΦA(C)⊥=ΦA(C)∩ΦA(C⊥)
由于ΦA(C)为双射,所以ΦA(C)∩ΦA(C)⊥=ΦA(C∩C⊥),故结论成立。
由定理2和定理5,得到如下结论。
定理6设A是F2上e+1阶方阵且AAT=J。设C是环R上长度为2s生成多项式为f(x)2s(e+1)的(1+λu)-常循环码,其中f(x)∈F2[x]是x-1的自互反因式。则ΦA(C)是F2上参数为[(e+1)2s,(e+1)(-degf)2s,≥d]的LCD码,其中d是F2上长度为2s生成多项式为f(x)2s的循环码的Hamming距离。
证明由引理1,|C|=2(e+1)(-degf)2s。由定理2,C是环R上(2s,2(e+1)(-degf)2s)的LCD码。由定理3和定理5,ΦA(C)是F2上参数为[(e+1)2s,(e+1)(-degf)2s]的LCD码。

φA(r)=(r0,r1,…,re)A≠0
即wG(r)=wH(φA(r))≥1。由此推出,对任意0≠c∈C,wG(c)≥wH(c)≥d。因此dG(C)≥d。由引理2,ΦA(C)的Hamming距离dG(C)≥d。
综上所述,结论成立。
运用定理6,可以构造F2上具有如下参数的LCD码。
推论1设A是F2上e+1阶方阵且AAT=J。设η是一个2m-1次本原单位根,其中m≥4为正整数。设C是环R上长度为2m+1-2生成多项式为[(x-1)f(x)f*(x)]2(e+1)的循环码,其中f(x)是η在F2[x]上的极小多项式,f*(x)是f(x)的互反多项式。则ΦA(C)是F2上参数为[(e+1)(2m+1-2),(e+1)(2m+1-4-4m),≥6]的LCD码。
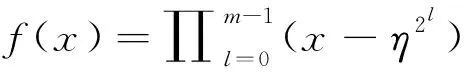
[(e+1)(2m+1-2),(e+1)(2m+1-4-4m)]
的LCD码。设D是F2上长度为2m+1-2生成多项式为[(x-1)f(x)f*(x)]2的循环码。下面证明dH(D)≥6。设D0是F2上长度为2m-1生成多项式为(x-1)f(x)f*(x)的循环码。由文献[27],dH(D)=dH(D0)。注意到η-2,η-1,1,η,η2是(x-1)f(x)f*(x)的零点,由BCH界,dH(D0)≥6,即dH(D)≥6。由定理6,结论成立。
3 结束语
本文研究了多项式剩余类环R=F2[u]/(ue+1)上的线性码的Gray象,给出了一种构造F2上LCD码的方法。首先,给出了环R上任意长度的(1+λu)-常循环码是LCD码的充要条件。其次,研究了环R上线性码的Gray象的代数结构。引入了一类特殊的Gray映射,给出了环R上长度为n的线性码的Gray象是F2上长度为(e+1)n的LCD码的充要条件。最后,利用环R上任意长度的(1+λu)-常循环LCD码的Gary象,构造了F2上的LCD,并得到了F2上一类Hamming距离大于等于6的LCD码。

