二维Poisson 方程中不完备边界及未知参数的反演

王 月，蒋 泉，2*

(1.南通大学 理学院，江苏 南通 226019；2.南通大学 交通与土木工程学院，江苏 南通 226019)

在工程中很多问题均归结于偏微分方程的求解[1-3]，其正的问题研究在理论和算法上已经较为成熟，但在反问题方面还需进一步开展深入的研究，例如：在已知部分区域边界条件的情况下，由观测点的函数值反演出Poisson 方程的未知的边界处函数值；或在函数中存在部分参数未知情况下，由观测点测量值及边界条件反演出函数的参数。Yang等[4]人利用简化Tikhonov 正则化方法探讨了半带型区域中含有一个变量的二维Poisson 方程未知源识别反问题，得到问题的正则近似解，并给出了正则解和精确解之间的Hölder 型误差估计；Hamad 等[5]人研究了Poisson 方程源函数反演迭代算法，其算法能够根据边界处的测量值反演未知源函数的近似估计，并得到了良好的结果；Koulouri 等[6]人通过贝叶斯近似方法研究了Poisson 方程的逆源问题，并将该方法用于脑电图成像，得到相对准确的结果；Rond 等[7]人将高斯去噪算法用于Poisson 噪声反问题中，解决了Poisson 定向问题的信噪比范围问题。

基本解方法(method of fundamental solutions，MFS)的实质是基本解函数的叠加[8-9]，在具体计算中不需要积分，可大大减少计算量，节约计算时间；同时具备应用性较强、易推广至高维领域的优点。Sun等[10]人利用MFS 对含边界噪声的热传导反问题进行了研究，其数值算例证明了该方法的稳定性和精确性；Karageorghis 等[11]人将MFS 引入到热弹性反问题，对MFS 形成的高维病态方程的正则化参数选取进行了分析，其数值结果具有较好的稳定性；Johansson 等[12]人对非定常热传导反问题进行了研究，进一步说明了MFS 具有高度的稳定性、耗费计算资源少的优点。

Kalman 滤波算法是处理反问题最为直接有效的方法之一，可以在系统状态空间表示的基础上，有效地处理测量数据噪声带来的不确定性，最终求得系统状态的最优估计，具有结构简单和易于实现的优点[13]。目前，Kalman 滤波器在工程系统中得到了广泛的应用，包括导航定位系统[14-16]、无人机的实时追踪[17]、雷达的目标追踪[18-19]等方面。同时在大气观测、仪器检测[20]等方面也得到了广泛的应用，如：Rincón 等[21]人结合Kalman 滤波器对输出进行偏差校正，给出了天气模型预测(WRF-ARW)的后处理分析，提高了整体预测值的正确率；Baptista 等[22]人研究了Kalman 滤波对剩余使用寿命估计值的适用性，结果表明该技术具有较好的精度和收敛性，大幅度提高了设备寿命回归模型的精度；Kang 等[23]人给出了基于惯性测量单元估计姿态和陀螺偏差的无迹Kalman 滤波算法，并通过实验和仿真进一步验证了该算法的有效性。

本文应用Kalman 滤波技术，对Poisson 方程数值求解问题中的不完备边界及未知参数反问题进行分析和研究。利用基本解方法对调和函数的边界值问题进行计算，对获得的高度不适定高维线性方程利用截断奇异值分解法进行数值求解；进一步通过Kalman 滤波技术，利用有限个观测点的函数测量值最终反演出未知边界处函数值和未知参数值。

1 基本方程

1.1 基本解方法

二维平面内区域Ω 上的泊松方程为

式中：φ 为区域中未知函数值；Δ2为Laplace 算子；q为已知函数；λ 为已知参数；Ω1为Dirichlet 边界；Ω2为Neumann 边界。

根据基本解方法原理，在二维问题中，区域Ω内的任何一点P，式(1a)中函数φ(P)可写成基本解函数的叠加[19-20]，

式中：Ci为待定系数；Q 为区域Ω 外的源点；n 为源点总数目；φ*(P)为式(1)的特解；G1(P，Qi)为齐次调和函数φ 解的基本函数，具体形式为

其中ri为点P 和Qi之间的距离。在直角坐标系中，如P 和Qi的坐标为(x，y)和(xi，yi)，则有如下关系：

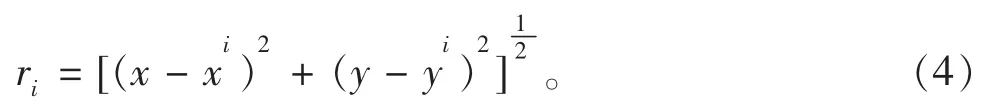
对于特解φ*(P)，当q 为常数时，可写成如下形式[24-25]：

当(xq，yq)处存在强度为q0的源点时，特解可为

根据边界条件(1b)和(1c)，式(2)中待定常数Ci可由如下的线性方程组求出：

式中：n 为边界点数；n1为Dirichlet 边界点数；n -n1为Neumann 边界点数。由上述方程组求出待定系数后，任意一点的函数值就可以按式(2)得到。

1.2 Kalman 滤波基本方程

根据Kalman 滤波理论，t 状态下的系统可由t -1 状态进行描述，其状态方程和观测方程可写成[13]

式中：Xt为状态向量；c 为系统矩阵；Wt为系统噪声；Zt为观测向量；Ht为观测矩阵，且当观测点的数目为m 时，Ht为m 维列向量；Vt为测量噪声。

Kalman 滤波计算过程如下所示：

1)预测系统状态

2)预测系统均方差

3)修正卡尔曼混合系数

4)修正系统状态

5)修正系统均方差

式中：I 为单位矩阵；a 为系统参数，对于静态问题一般为单位矩阵；为先验估计；为后验估计；和Pt为预测系统均方差和修正系统均方差；Kt为卡尔曼增益矩阵；Q 为过程噪声方差；R 为测量噪声方差。

对于非线性测量系统，观测方程(7b)通常用下式来描述：

当h(Xt)足够平滑时，为了线性化，可在先验估计Xt=处泰勒展开成[26]

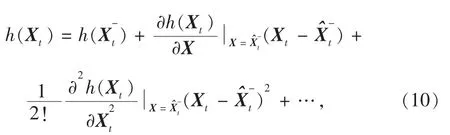
将观测矩阵Ht写成

略去高次项，有如下关系：

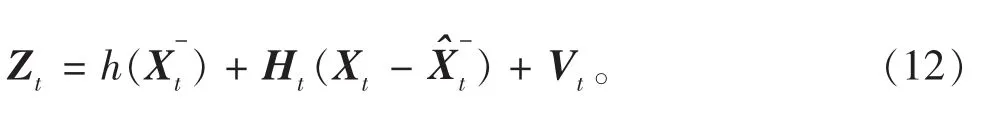
定义新的观测向量ηt，满足

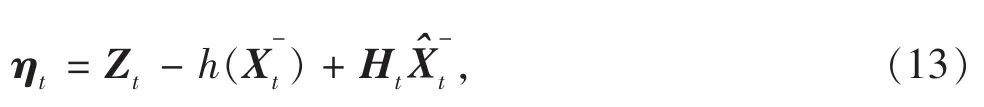
可将观测方程(7b)改写成

则式(14)可应用线性系统的Kalman 滤波，称为扩展Kalman 滤波。

2 数值算例

2.1 未知边界问题反演

如图1 所示，以直角坐标系中2a × 2h(a = 10，h = 10)矩形区域Ω 为例，在区域中函数φ 满足Δ2φ= 0，边界条件定义如下：

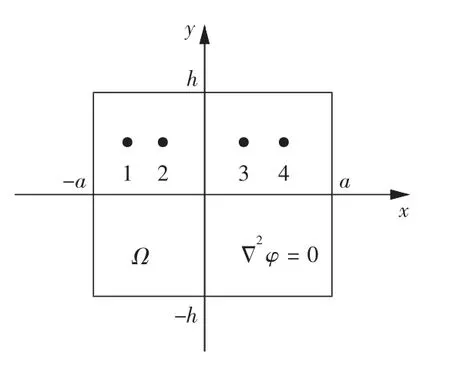
图1 边界问题区域Fig.1 Domain of the problem

式中φ(1)、φ(2)和φ(3)分别为已知边界函数值。根据式(15)，该区域内函数存在如下形式的解析解φana：

根据式(16)，区域Ω 在x 轴以下的边界并未给出，此问题的边界条件不完整，仅利用基本解方法计算不能得出准确的数值解。

不失一般性，令式(3)中λ = 1，取4 个观测点(如图1 所示)，以观测点处的解析解为测量值，利用Kalman 滤波方程(8a)—(8e)进行计算，此时c 为4 ×4 单位矩阵，Ht为4×1 维向量。在具体计算过程中，定义测量后验估计和先验估计的相对误差δ1为

函数计算值与解析解相对误差δ2为

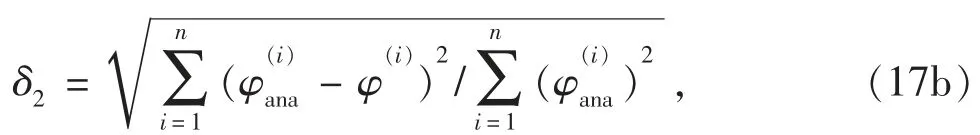
式中n 为所取测试点总数。

根据式(8a)—(8e)，Kalman 滤波过程为

2)根据基本解方法可以算出待定系数Ci，并由式(16)计算观测点的实际值；

4)第2 次计算时，重复以上步骤，直到相对误差δ1小于0.01%时结束计算。

对4 个观测点以不同的初始预测值(-30和-50)进行Kalman 滤波，结果如图2 所示。从图2可以看出：在不同初始预测值情况下，通过滤波均能收敛于解析解，且相对误差δ1可控制在0.01%以内；滤波速度快，滤波3 次后即可收敛至实际值，并在收敛过程中，具有良好的鲁棒性。

图2 未知边界问题Kalman 滤波结果Fig.2 Kalman filtering results of unknown boundary problems

图3(a)和(b)分别给出了研究区域内不完备边界y=-h 处的函数及其导数∂φ/∂n 的数值解和解析解的对比情况。由图3 可知，通过Kalman 滤波，在未知边界上函数数值解与解析解的相对误差δ2在5%以内，充分证明了Kalman 滤波技术在未知边界反演问题中的有效性。

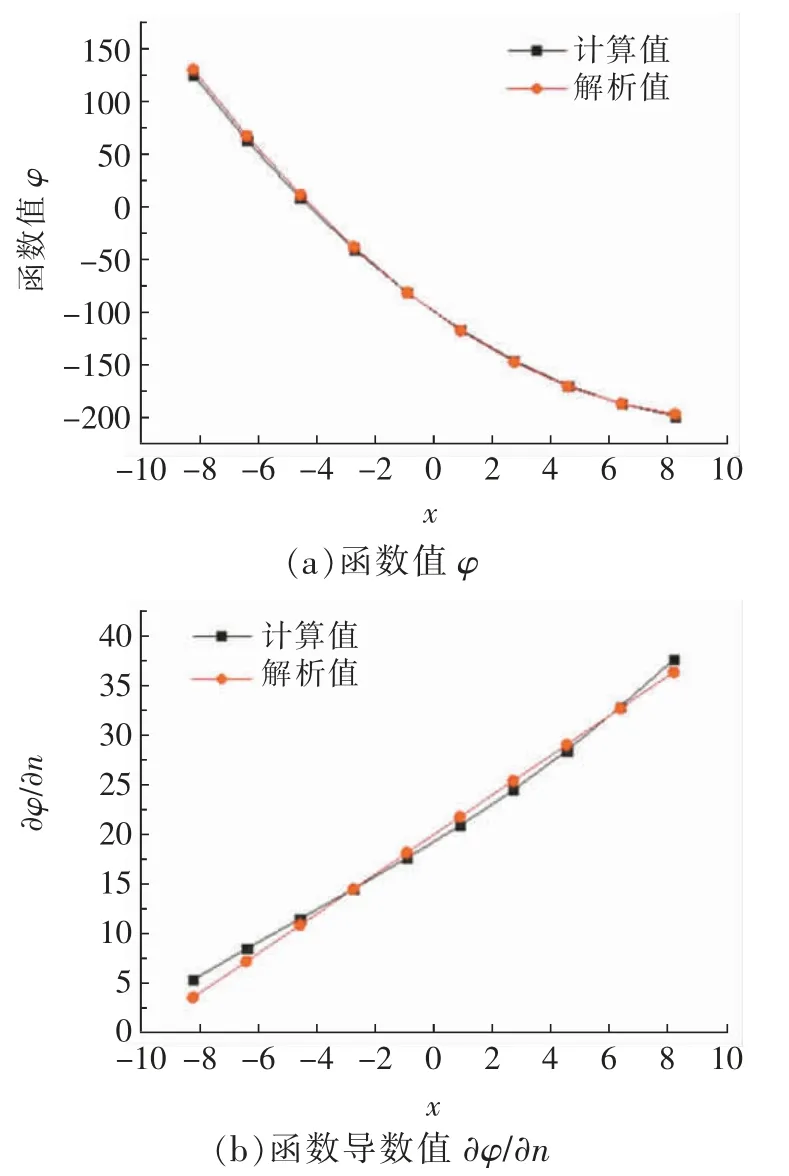
图3 边界y=-10 处计算值与解析解对比Fig.3 Comparison of calculated value and analytical value at boundary y=-10

2.2 未知参数反演

如图1 所示，同样以2a × 2h(a=10，h=10)矩形区域内的二维Piosson 方程为例，进行参数反演研究，为扩展Kalman 问题。考虑到λ 为常数，取目标参数ε=1/λ 进行Kalman 滤波。本问题的边界条件定义如下：

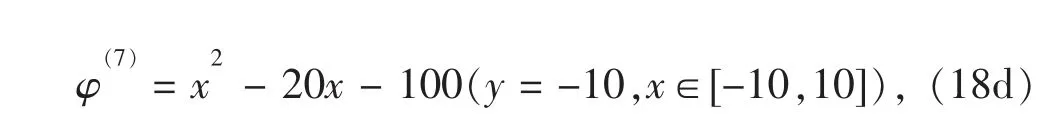
式中φ(4)、φ(5)、φ(6)和φ(7)分别为已知边界函数值。则该区域内φ 函数同样存在解析解(16)，且常数目标值ε=8(λ=1/8)。

同样在区域内取4 个观测点，分别利用不同初始预测值ε=20 和ε=50 进行滤波，结果如图4(a)和(b)所示。由图4 可以看出，参数的初始值在经过两次滤波之后就趋于实际值ε=8，且相对误差δ1在0.01%以内，表明该方法对未知参数反演问题有效。

图4 未知参数问题Kalman 滤波结果Fig.4 Kalman filtering results for unknown parameter problems

利用反演参数对y=0 处的函数φ 及其导数进行对比，结果如图5 所示。由图5 可以看出，在边界y=0 上得到的函数及其导数的计算值与解析解相对误差在0.05%以内，证明了本方法的有效性。

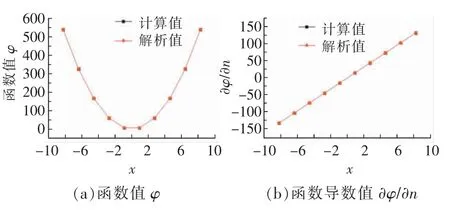
图5 y=0 处计算值与解析解边界条件对比Fig.5 Comparison of calculated value and analytical value at boundary y=0

3 结论

本文采用基本解方法和Kalman 滤波技术相结合，对存在不完备边界和未知参数的Poisson 方程的反问题进行研究和计算，通过观测点的测量值反演出未知的边界值或参数值。通过数值算例可以看出，利用该方法得到的数值解与解析解之间的误差小，收敛速度快，鲁棒性强，显示了本方法的有效性。该方法可为电磁学、渗流、热传导等工程领域具体问题的数学建模、数值分析提供参考，为反问题的分析研究提供思路。