单步和多步寻优结合的诊断策略构建方法*
杜小帅,胡冰,施端阳,张馨予
(1.空军预警学院,湖北 武汉 430010;2.中国人民解放军94005部队,甘肃 酒泉 735000)
0 引言
随着高新科技的发展和应用,武器装备的结构和功能越来越复杂化、精细化,其使用条件和战场环境的恶劣程度日趋提升,对装备的测试与诊断提出了更高的要求。而要解决这一问题则需要采用“并行工程”的思想,在装备设计阶段就使其具有良好的测试性。诊断策略设计是测试性设计和分析的一项重要内容[1],是提高故障诊断效率、改善装备故障诊断能力、降低全寿命周期费用的关键。GJB 2547A-2012将诊断策略定义为“综合考虑规定约束、目标和有关影响因素而确定的、用于依据观测数据进行故障诊断的测试判断逻辑”[1]。
Pattipati证明诊断策略问题是NP-Complete问题[2],穷举法虽然能够得到最优解,但计算时间随问题复杂程度成指数性增长。为降低计算复杂度,国内外学者将启发式搜索方法应用在诊断策略构建问题中。AO*算法[2-3]主要以霍夫曼编码平均字长构造启发式评估函数,根据启发式评估函数估计测试费用的下界值,通过不断回溯修正找到测试费用最小的诊断策略,但回溯操作大大增加了AO*算法的计算复杂度。信息熵算法[4-5]等单步寻优搜索方法每次只选择符合约束条件的最优测试,计算速度快,但最优性较差。多步寻优搜索方法[6]在单步寻优搜索方法的基础上预先生成MSTEP层部分诊断树[7],通过计算部分诊断树的诊断效果判断测试的优劣。由于考虑了多步测试的共同信息,其最优性比单步寻优搜索方法好。Rollout算法[8-9]以信息熵算法为基准策略生成完整的诊断树,通过回溯迭代找到比基准策略更为精确的结果,计算量较AO*算法小,但也存在回溯操作。Growing算法[10]将隔离单个故障的测试分为基本测试和不必要测试,在构建诊断策略时,先选择故障,后确定测试,按照先验概率的大小顺序隔离故障,生成不包含不必要测试的测试序列,但是当故障的先验概率相近时,其最优性不佳。
针对上述问题,本文以自上而下构造诊断策略的思想为基础,提出了一种根据故障状态模糊集的概率分布情况选择单步或多步寻优搜索方法的诊断策略构建方法。首先分析了单步寻优搜索方法特点和不足。然后以隔离单个故障为目标,得到一种无回溯的多步寻优搜索方法,并将单步寻优搜索方法与多步寻优搜索方法相结合,使先验概率较大的故障具有较少的测试步骤和费用。最后对实际案例进行了应用研究和分析计算,通过与信息熵算法、Rollout算法和AO*算法的诊断结果进行对比,验证了方法的有效性。
1 诊断策略问题描述
1.1 诊断策略模型描述
故障诊断策略问题可描述为五元组:
(1)F={f0,f1,…,fm}为装备故障状态集,包含装备所有的故障状态,其中,f0是无故障状态,fi(i=1,2,…,m)表示当且仅当第i个故障发生时的故障状态。
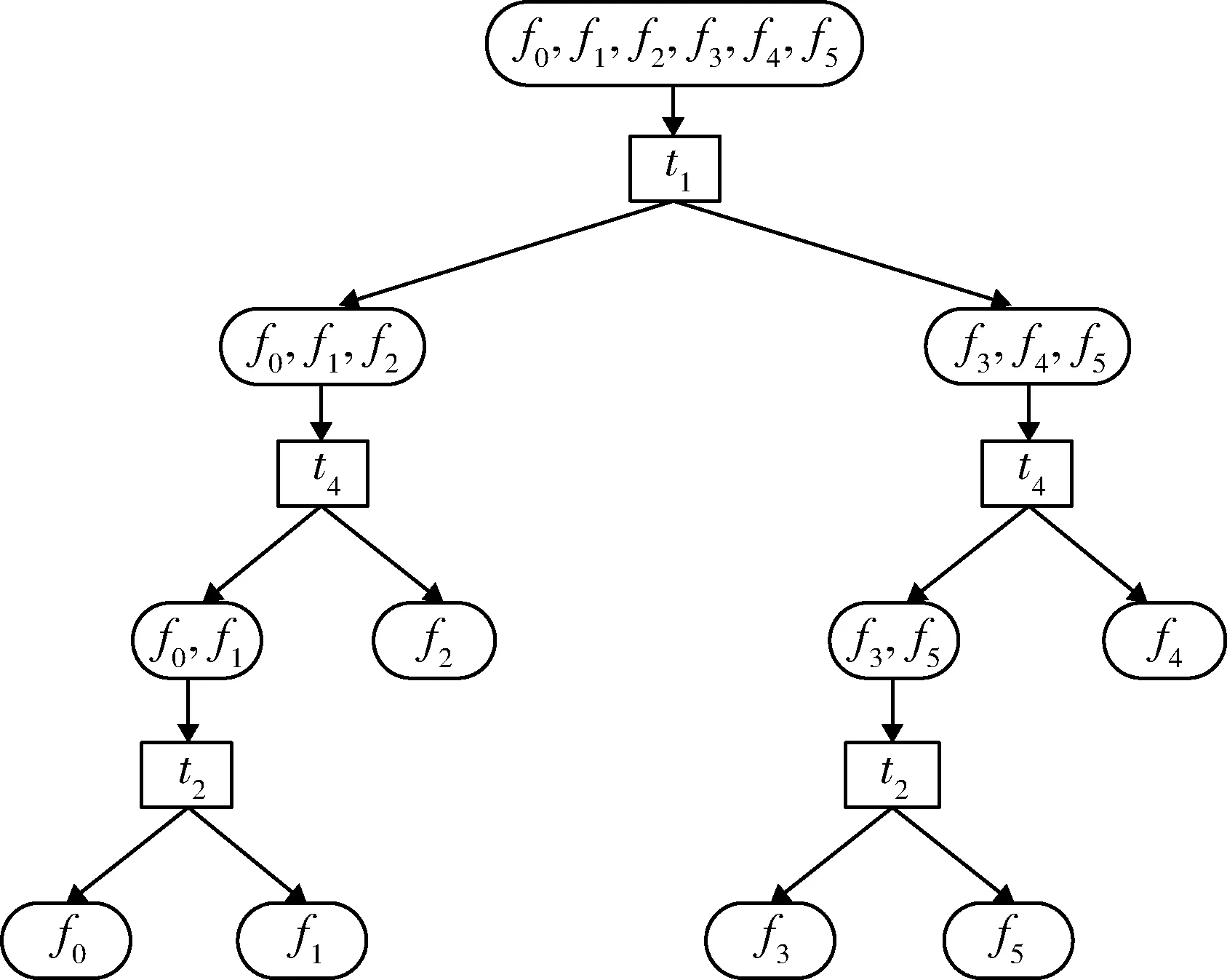
(2)P={P(f0),P(f1),…,P(fm)}表示与装备m+1个故障状态对应的先验概率集合,满足0 (3)T={t1,t2,…,tn}为装备的测试集,规定测试只有通过、不通过2种情况,且测试结果可靠。 (4)C={c1,c2,…,cn}表示n个测试对应的测试费用的集合,其中cj表示执行测试tj所需的费用。设定测试费用为无量纲的物理量。 (5)D=(dij)(m+1)×n为故障-测试相关矩阵,用来描述故障模式集和测试集的依赖关系。相关性矩阵是装备测试与诊断的基础。矩阵行表示故障状态,列表示测试,矩阵中的元素dij表示测试与故障状态的相关性,其值为0或1。dij=1表示测试tj可以检测故障fi,即故障发生时,测试不通过;dij=0表示tj不能够检测故障fi,即故障发生时,测试通过,d0j=0,∀j。 按照诊断策略的测试执行顺序,每个测试执行后,根据结果推测装备的故障结论。设装备故障状态模糊集为X,用测试tj检测X有通过(dij=0)和不通过(dij=1)2种输出,分别记为Xj0和Xj1。推理机是装备故障状态逻辑推断的推理方法。X到Xj0和Xj1过程的推理方法就是推理机。 且 X被测试tj划分为2个子集Xj0和Xj1。 在故障诊断隔离过程中,会产生相应的测试费用,测试费用期望值的计算公式为 式中:J为测试费用的期望值;Di为诊断树D中隔离出故障fi的测试序列,|Di|为该序列的长度;cDi[k]为序列Di中的第k个测试的费用;P(fi)为故障fi的先验概率。 最优诊断策略构建的目的是,当装备发生故障时,能够按照给定逻辑和顺序选择测试,快速检测和准确隔离故障,并且使得测试费用期望值最小,其计算公式为 Dopt表示不模糊的隔离全部故障且平均测试费用最少的诊断策略。 单步寻优搜索方法每次只确定一个测试,通过构造启发式评估函数,每次选择使启发式评估函数达到最优的测试,根据测试结果诊断隔离故障,划分故障模糊子集,并不断向下拓展。由于单步寻优搜索方法仅考虑当前最优的测试,因此也被称为贪婪搜索方法。信息熵算法以最大化单位费用信息增益为优选测试的依据并构造启发式评估函数[4],是应用最广泛的贪婪搜索方法,其启发式评估函数为 式中:IG(X;tj)表示测试tj与故障状态模糊集X的互信息,即使用测试tj诊断待隔离故障状态模糊集而得到的信息量。 分辨力启发式评估函数[11]与式(8)等价: 通过对第1节的分析可知,诊断策略构建与无噪声编码之间具有相似性[12]:测试结果对应二元信息;故障状态集中各故障的测试步骤数对应信源的编码长度;诊断树的平均测试步骤数对应平均编码长度;最优诊断策略对应最小化交叉熵。要使交叉熵最小,则概率较大的元素应具有较小的编码长度。故在诊断策略构建问题中,应使先验概率较大故障具有较少的测试费用和测试步骤数。 信息熵算法考虑了故障发生概率、故障-测试相关性和测试费用等因素,但其在选择测试时,只考虑单步测试所获取的信息,而没有考虑所选测试对整体费用和后续测试的影响。因此以信息熵算法构造诊断策略,不能保证先验概率较大的故障对应较少的测试费用和测试步骤数。 以文献[2]的相关性矩阵为例,分析信息熵算法的实现过程及特点,其相关性矩阵如表1所示。给定测试费用为{5,10,15,5,20}。 表1 相关性矩阵Table 1 Dependency matrix 信息熵算法具体步骤可参考文献[4],其生成的诊断策略如图1所示。 故障f0的先验概率在故障状态集中占有较大比例,应该以较少测试步骤和费用对其进行诊断隔离。在图1中,故障f0对应的测试序列为[t1,t4,t2],但对表1的相关性矩阵分析可知,使用测试t2,t4即可隔离故障f0,故t1为此测试序列中的多余测试[10]。 图1 信息熵算法的诊断策略Fig.1 Diagnostic strategy based on greedy algorithm 信息熵算法作为单步诊断策略构建方法,在生成诊断策略时只考虑当前最优的测试。在表1的实例中,t1使单位费用信息增益达到最大值,故信息熵算法选择t1为第1步最优测试。然而仅得到t1而不考虑后续测试,则会增加f0的测试序列长度与测试费用,从而会相应地增加诊断策略的整体测试费用。 为使诊断策略的整体期望测试费用最小,则先验概率较大的故障应该具有较少的测试费用和测试步骤数,所以需要研究隔离单个故障的测试序列生成方法,综合考虑多步测试对整体费用的影响。 2.2.1 隔离单个故障的测试集生成方法 若故障fi能被测试集T隔离,则在以T为列的相关矩阵DT中,故障fi所在的行必须与其他行相异[13]。因此故障可隔离的条件可以表示为 式中:符号Π为“逻辑乘”;符号⊕为“异或”运算;T fi,T fj分别为fi,fj在矩阵DT中所对应的行向量;假设故障模糊集包含m+1个故障状态。 隔离2个故障的条件是,在相关性矩阵中,2个故障对应的行向量相异。其中,相异元素对应的测试能够隔离这2个故障。用逻辑“或”表示对应的测试,得到隔离2故障的测试方案,用I(fi,fk)表示为 式中:符号∑为“逻辑加”。例如,I(fi,fk)=t1+t2表示t1或t2可以隔离故障fi和fk。其中,符号“⊕”表示逻辑“或”。称集合Tik={t1,t2}为隔离故障fi与任意故障fk的隔离测试集: 式(13)得到隔离故障fi与任意故障的测试方案,若将所有的测试方案做累积运算,可得到隔离故障fi的所有测试组合,不妨将I(fi,F)表示隔离fi的测试方案: 把式(14)完全展开成“与或”式,显然每一个“与”式均能表示隔离fi的测试组合,各测试组合中元素组成的集合称为隔离故障fi的诊断隔离测试集,由此,可得到故障fi的一组诊断隔离测试集去除其中的真超集,得到故障fi的所有最小诊断隔离测试集。例如,故障集F中有3个 元 素,I(f1,f2)=t1+t2,I(f1,f3)=t1+t3,由 式(14)可 得I(f1,F)=t1+t1·t2+t1·t3,表 示t1,t1与t2,t1与t3均 可 隔 离故障f1。其中,符号“·”表示逻辑“与”。由此,可得到故障f1的诊断隔离测试集为{t1},{t1,t2},{t1,t3}。显然,{t1}为故障f1的最小诊断隔离测试集。 诊断隔离测试集具有以下2个性质: (1)故障fi的诊断隔离测试集为其所有隔离测试集并集的子集: (2)故障fi的诊断隔离测试集与其每个隔离测试集的交集都不为空集: 2.2.2 测试排序 2.2.1 节仅能确定隔离单个故障的测试集,若要生成测试序列,则需要进一步确定最小诊断隔离测试集中的测试顺序。多步寻优搜索方法可以看作单步寻优搜索方法的多次叠加过程,且在最小诊断隔离测试集中不存在多余测试,因此采用信息熵算法对最小诊断隔离测试集中的测试进行排序。 以表1的相关性矩阵为例。{t1,t2,t3}是故障f0的一个最小诊断隔离测试集,且初始故障状态模糊集X=F。由于隔离故障f0的测试集已经确定,则其测试费用也已确定,其在测试排序过程中能够提供的信息量为0。因此,在测试排序前首先需要更新故障状态模糊集及故障概率。X′=F-f0,P′(fi)=P(fi)/利用式(8)计算各测试的单位费用信息增益的值为0.093 8为0.097 1,为0.066 5。因此,选择t2为第1步最优测试。根据测试结果将X划分为2个子集{f0,f2,f3}和{f1,f4,f5}。将包含f0的子集赋予X,更新各子集的故障概率,选择t1为第2步测试,因此得到测试序列为[t2,t1,t3]。 2.2.3 测试序列优选 为获得最优的诊断策略,达到使测试费用期望值最小的目的,需要在确定待检测故障的所有最小诊断隔离测试集和相应的测试序列后,以费用最小为原则选出最优的测试序列。 假设存在故障状态模糊集X和故障fi,且fi∈X,fi的测试序列记为Di。隔离故障fi的期望测试费用记为J(fi) 式中:|Di|为测试序列Di的长度;cDi[k]表示序列Di中第k个测试的费用。 测试序列Di不能隔离故障状态模糊集中的所有故障,因此在隔离故障fi时,会产生一组故障状态模糊子集(X1i,X2i,…,Xl)i,由于X(rir=1,…,l)是伴随诊断隔离故障fi产生的,所以称其为故障fi的伴生故障集[10]。对每个伴生故障集,使用式(18),(19)更新其故障状态的概率: 伴生故障集的期望测试费用为 式中:Dri为伴生故障集的测试序列,由于是在隔离故障fi的过程中产生的,故由故障fi的测试序列Di决定;||表示测试序列的长度表示测试序列中第h个测试的费用。 若要生成完整的诊断策略,需进一步隔离伴生故障集中的故障,故障隔离过程会产生相应的测试费用。因此,全面评估整体测试费用,需要对伴生故障集的隔离费用进行估计。霍夫曼编码[14]被称为最佳编码,能够按照字符出现概率构造平均长度最短的码字。对故障集,其期望测试步骤的下界值可用霍夫曼编码的平均字长近似估计。将备选测试集中测试的费用按照由小到大的顺序进行排序(0≤c1≤…≤cn),将霍夫曼平均字长与备选测试集中对应测试的费用相结合,可以得到基于霍夫曼编码的测试费用评估函数[15]。由此,可对伴生故障集的最小故障隔离费用进行估计: 式中:h(Xri)为故障状态模糊集Xri的最小测试费用估计函数,该函数给出了故障状态模糊集Xri故障隔离费用的下界;L(*Xri)为故障状态模糊集Xri的霍夫曼编码平均字长;为取下整数;L(fj)为fj对应的霍夫曼编码长度。 用h(X,fi,Di)表示使用测试序列Di隔离故障fi,并构造完整诊断策略的测试费用估计值: 将式(17)~(21)代入式(23)可得 选择使h(X,fi,Di)达到最小的测试序列为隔离故障fi的最优测试序列。由此,可得多步寻优搜索方法的启发式函数: 要使先验概率大的故障对应较少的测试费用和测试步骤数,同时考虑诊断树整体的测试费用,则需要根据故障状态模糊集中的故障概率分布情况,选择使用单步或多步寻优搜索方法。由于单步和多步寻优搜索方法均采用自上而下的方式构造诊断树,故在优选方法时,利用费诺编码的原理对故障状态模糊集进行分析。 将故障状态模糊集中的故障按概率大小进行降序排列(P(f1)≥P(f2)≥…≥P(fz)),在此顺序中,选择一处断开位置,将故障状态模糊集划分为2组,使每组概率和最接近相等。当其中一组只含有单个故障f1时,则优先隔离f1,使用多步寻优搜索方法生成隔离f1的测试序列;否则,使用信息熵算法选择诊断当前故障状态集的最优测试。 根据分辨力函数的性质,概率和乘积越大,则两者越接近。则故障优先隔离条件可表示为 当故障状态模糊集中故障概率满足式(26)时,说明fi单独为一组时,2组的概率和最接近相等,则认为隔离fi的测试费用对整体费用具有较大的影响,使用多步寻优搜索方法优先隔离f1;否则,使用单步寻优搜索方法。 步骤1初始化五元组。令X=F,创建一个集合FS存放故障模糊子集。 步骤2使用式(27)更新X中各故障的概率: 步骤3生成X的备选测试集合T′(包含求解节点X的过程中没有用过的测试)。根据下列步骤,选择单步或多步寻优搜索方法。 (1)将X的故障按概率降序排列。 (2)优选诊断策略构建方法,当X中故障满足式(26)时进入步骤4,否则进入步骤5。 步骤4隔离X中概率最大的故障fi并生成其对应的最优测试序列。 (1)根据式(12)~(14)得到故障fi的诊断隔离测试集,去除其中的真超集,得到fi的最小诊断隔离测试集。 (2)利用信息熵算法的启发式评估函数对最小诊断隔离测试集中的测试进行排序,得到隔离故障fi的测试序列。 (3)根据式(24)计算各测试序列的费用估计值,选择使h(X,fi,Di)达到最小的测试序列为fi的最优测试序列。使用最优的测试序列隔离故障fi,生成诊断树的部分图解,并得到fi的伴生故障集(X1i,若伴生故障集Xri中元素个数大于1,则将Xri加入集合FS。 步骤5使用信息熵算法的启发式评估函数从备选测试集中选择当前最优测试,根据测试结果划分故障子集,若子集中元素大于1,则加入FS。 步骤6重新取X为FS中的元素,重复步骤2~5,直到FS中元素个数小于1。 以表1相关形矩阵为例,说明单步和多步寻优结合的诊断策略构建方法的实现过程,其生成的诊断树如图2所示。 X=F,将X中故障按概率大小降序排列(0.7>0.12>0.10>0.05>0.02>0.01)。根据式(26),优选诊断策略构建方法。X中元素满足0.7×(1-0.7)>0.82×(1-0.82),即将先验概率最大的故障f0单独划为1组时,划分的2组概率和最为接近,所以首先隔离故障f0,使用多步寻优算法生成隔离f0的测试序列。 根据式(12)~(14)得到f0的最小诊断隔离测试集为{t2,t4},{t1,t2,t3},{t1,t3,t5},{t1,t4,t5},{t2,t3,t5},使用信息熵算法对测试集中的测试进行排序,得到f0的 测 试 序 列 为[t4,t2],[t2,t1,t3],[t1,t3,t5],[t4,t1,t5],[t2,t3,t5]。 根据式(24)选择隔离故障f0最优的测试序列。测试序列[t4,t2]使h(X,f0,Di)达到最小值,故选择[t4,t2]为隔离故障f0的最优测试序列,得到伴生故障集{f1,f4},{f2,f3,f5}。 选择t1为诊断故障模糊子集{f1,f4}的最优测试。对模糊子集{f2,f3,f5},使用式(27)更新子集中的故障概率,对故障模糊子集中的故障按概率降序排列(0.5>0.416 7>0.083 3),其中f5满足式(26),则优先隔离f5。 根据式(12)~(14)得到f5的最小诊断隔离测试集为{t2},{t1,t3},{t1,t5},对集合中的测试进行排序,得到隔离f5的测试序列为[t2],[t1,t3],[t1,t5]。其中,[t2]使诊断策略的费用估计值达到最小,故选择[t2]为隔离故障f5的最优测试序列,并得到伴生故障集{f2,f3},[f5]。 选择t1为诊断故障模糊子集{f2,f3}的最优测试,从而得到完整的故障诊断策略。 通过式(6)计算,得到图2的测试费用期望值为15.9。图1所示信息熵算法得到的诊断策略的测试费用期望值为19.3。使用AO*算法及Rollout算法对相关性矩阵进行处理,得到测试期望值费用为15.9。本文方法得到的测试费用与AO*算法及Rollout算法相同。 图2 本文方法的诊断策略Fig.2 Diagnostic strategy in this paper 为说明方法的有效性,同时对比信息熵算法、Rollout算法与AO*算法的诊断效果,以导弹姿态稳定分系统[16]、舰炮制导弹药控制系统[17]、卫星电源系统[18]等3个实际的测试性模型及相关性矩阵为例进行分析计算,计算结果如表2所示。 表2 测试费用期望值对比Table 1 Comparison of the expected text cost 由表2可知,在本文所列举的3个案例中,单步和多步寻优结合的诊断策略构建方法在避免回溯操作的同时,计算结果优于信息熵算法,与Rollout算法及AO*算法的测试费用相同。 在诊断策略构建问题中,要使测试费用的期望值尽可能小,则先验概率较大的故障应该对应较少的测试步骤和测试费用,所以应根据故障概率情况确定诊断策略构建方法。单步和多步寻优结合的诊断策略构建方法综合考虑了测试费用、故障概率以及多步测试信息的影响,在避免回溯操作的同时能够以较低的测试费用对装备进行故障诊断和隔离,具有一定的理论和实际应用价值。1.2 故障诊断推理机



1.3 最优诊断策略


2 单步和多步寻优结合的诊断策略构建方法
2.1 单步寻优搜索方法



2.2 多步寻优搜索方法



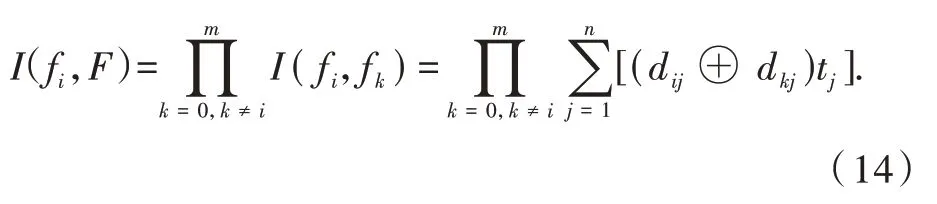





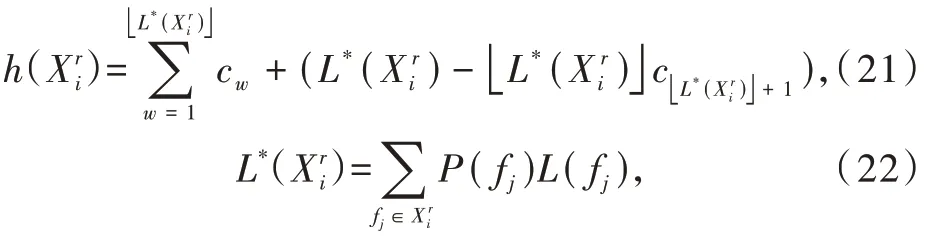



2.3 诊断策略构建的方法优选
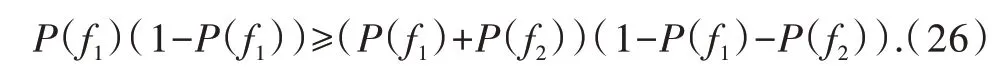
2.4 详细步骤

3 实例验证
3.1 仿真计算
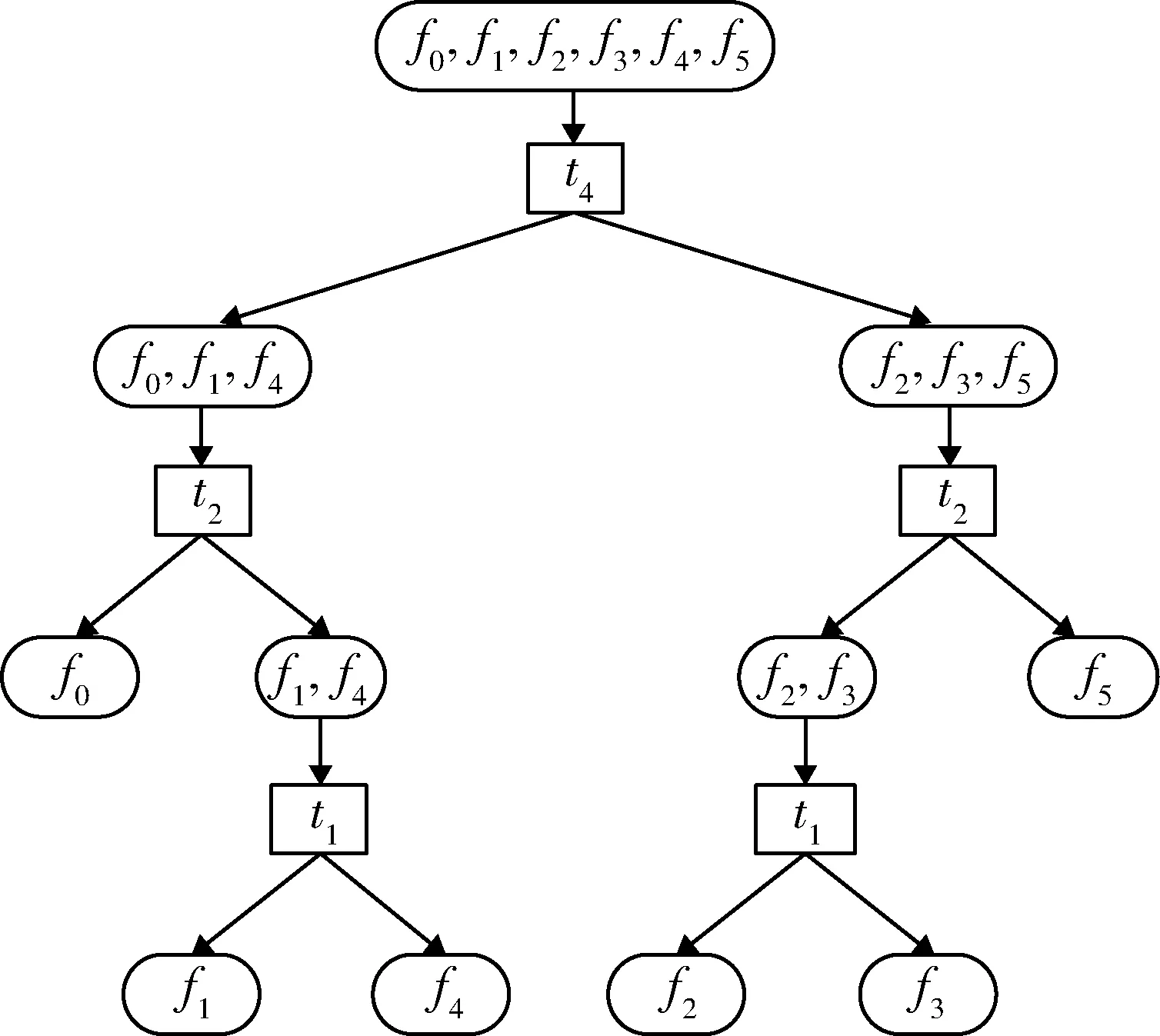
3.2 实例分析
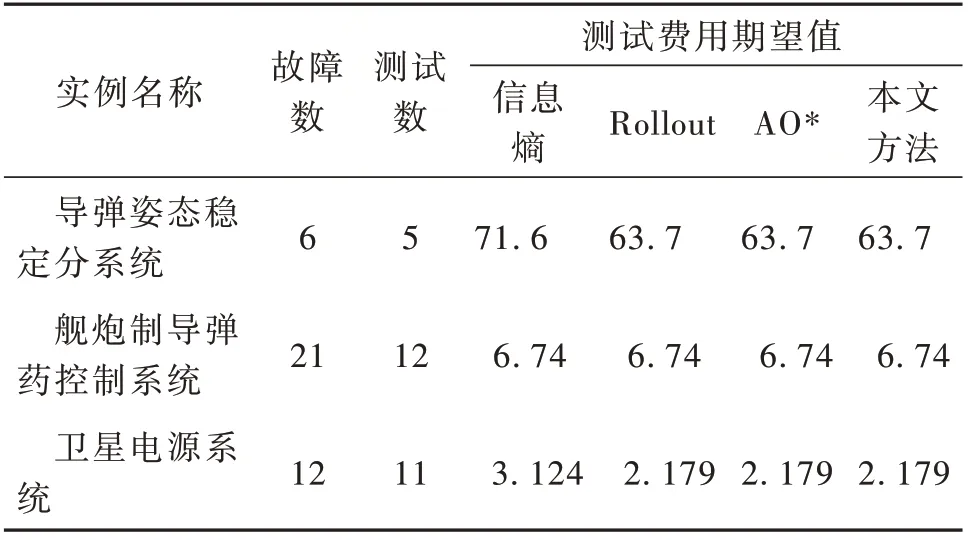
4 结束语

