计算错误找原因、解答粗心寻对策
⦿上海七宝中学 肖 岚
1 引言
教学中经常碰到这样的学生,思维敏捷,一点就通,但就是计算频错、粗心不断.本文中梳理了一些原因,不过高中数学题目综合性强,原因多种多样,互相影响,相互作用,恶性循环,此处不可能面面俱到,只求抛砖引玉.分析问题所在的同时,尝试更新和设计针对性练习,采取有效可行的方案,长期不断坚持下来,让学生们从中受益.教与学正是这样做而获其惑,惑而求其解,解而求其用,不亦乐乎?
2 错因分析
2.1 心理性问题
2.1.1 没有信心,裹足不前
不能洞见条件和结论的联系,没有目标,也不敢尝试.消极的心理暗示容易造成优柔寡断,墨守成规.

认定函数y=f(x)关于点(m,n)成中心对称的充要条件是对定义域中任意x,都有f(x)+f(2m-x)=2n.那么,不要犹豫!目标明确!没有退路!立马计算!

我们发现无论多少字母只要抓住关键点都能迎刃而解,此时教师辅以适当的鼓励,对学生心理产生积极暗示,长此以往,提升学生数学自我效能感.先在心理上突破,再在方法上突破.
2.1.2 计算内容缺少故事性,学习情绪没有起伏
教师可以根据学生认知规律设计有故事的组团式练习(变式练习、探究练习等),让学生在解锁一个个问题时有过关斩将的情绪波动,从而更好地内化知识、优化运算.数学用数字编码世界,心理用人性编码世界.数学问题需要对编码储存、提取.当一个问题被各种角度编码时本质就会更完整地呈现、记忆会更加深刻,这样建立的知识结构更有高瞻远瞩性.高中数学为我们提供了很多这样的契机,下面举一例由三个问题构成的组团练习.
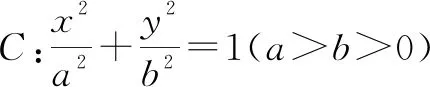
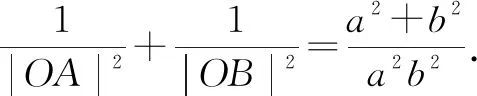



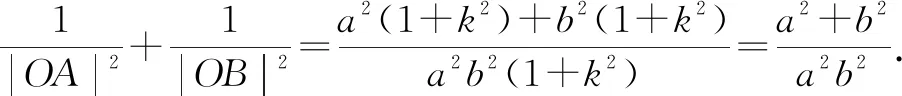
图1

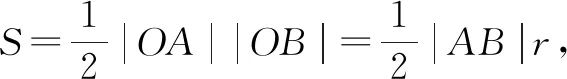
|OA|2|OB|2=(|OA|2+|OB|2)r2.
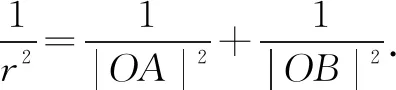

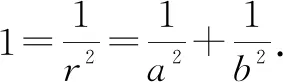
问题一的定值放在直角三角形中就是斜边上高与直角边关系,于是有了问题二;定值的逆代求范围也是对不等式的灵活运用,于是有了问题三.学生发现它们的联系后思考的维度被打开了,对某些定值的复杂运算也不再抗拒了.计算有方法,问题有源头,解答有乐趣.这三个问题包括组合性、逆向性、结合性、同一性等变式设计.让学生对数学的学习有更深和更全面的认识和理解.当题目的外延增大时,计算会变得更有意义.
2.2 逻辑性问题
2.2.1 转化时疏忽等价性
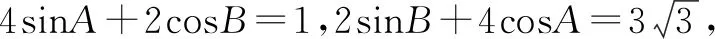
分析:
4sinA+2cosB=1
①
②
由式①、式②平方和得:
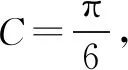

学生因为没有意识到平方不一定是等价变形,很可能产生增根.错误地保留了2个答案.
另外,充分不必要条件会造成失根,必要不充分条件则易造成增根.
2.2.2 片面不严谨,审题不严密,挖掘信息不够全
例3设数列{an}的通项公式为an=pn+q(n∈N*,p>0).数列{bn}定义如下:对于正整数m,bm是使得不等式an≥m成立的所有n中的最小值.
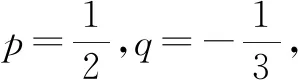
(2)是否存在p和q,使bm=3m+2(m∈N*)?若存在,求p和q的取值范围;若不存在,请说明理由.
解:(1)略.
(2)仔细审题,条件一:n=3m+2满足an=pn+q≥m(n∈N*,p>0),所以有p(3m+2)+q≥m.
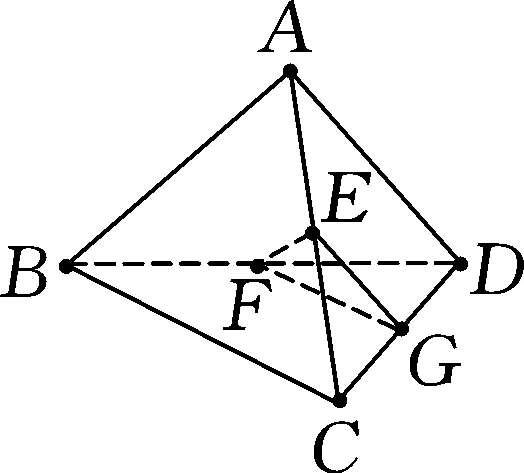
条件二:n=3m+2是最小的满足an=pn+q≥m(n∈N*,p>0)的解,再小不行了,所以有p(3m+1)+q 三个条件缺一不可,而学生通常不能全部挖掘,自然就算不出答案.逻辑是思维品质的中心环节.清晰、严密、理性和严谨是数学最重要的特点之一. 以不等式为例,没有深刻理解不等式的性质:误认为分母为正;取倒数时想当然认为分母越大分数越小;移项时正负号混乱. 例4直线y=kx+1与双曲线x2-y2=1的左支分别交于A,B两点, (1)求k的取值范围; (2)直线l过点P(-2,0)及线段AB的中点,CD是y轴上一条线段,对任意的直线l都与线段CD无公共点,试问CD长得最大值是否存在. (1-k2)x2-2kx-2=0 (取倒数时很多学生会不注意分正负情况,忽略不等式的性质做出错误答案.) 这类问题建议择机择时订正,建议分行写步骤,建议限时训练,建议整理错题本. 不同的策略计算量大不相同,寻找最佳策略、优化解题方法可以规避复杂的运算和人为陷阱. 策略1:沉溺于多字母代数处理剪不断理还乱. 图2 设AB中点为C(x,y),在等边△OAB中可得: 例6空间四边形ABCD中,E,F分别是AC,BD的中点,AD=6,BC=8,且AD与BC成60°角,求线段EF的长. 很多同学没有深刻理解异面直线所成角的概念,只给了一种答案,漏了A′BCD这种情况(如图4). 图3 图4 布鲁纳曾经说:“学生的错误都是有价值的.”运算错误和粗心大意不是独立存在的,是以上种种问题导致的多米诺效应,互相影响,很有可能导致数学焦虑,进而影响毅力、自我效能感,最终影响数学成绩.提高运算能力减少粗心发生实际上是一种综合能力的提高.教师层面上,应该更充分理解学生的认知心理、认知过程,确定学生自己的操作运输、知识存储、组织情境的方法,使学生能够积极地参与到情感沟通中,教师鼓励越多,学生收获越大,能力提高越快.学生层面上,应该优化记忆系统,提高感觉、知觉、视觉等观察品质,减少错觉,审题全面;注重新旧知识联系、正反两方面论证、总结归纳类比,逐渐丰富知识结构,促进数学学习的整体观念;多加练习、经常反思、深思熟虑,形成在解题中集中而稳定的注意力;增加学习的动机和自我要求,突破一些关于数学的消极和情绪化的信念,更多正面自我暗示.Z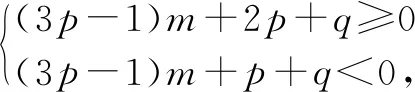
2.3 知识性问题
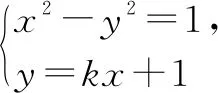

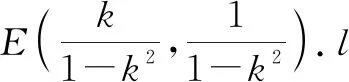


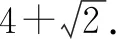
2.4 策略性问题
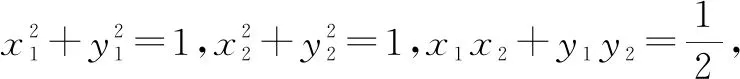
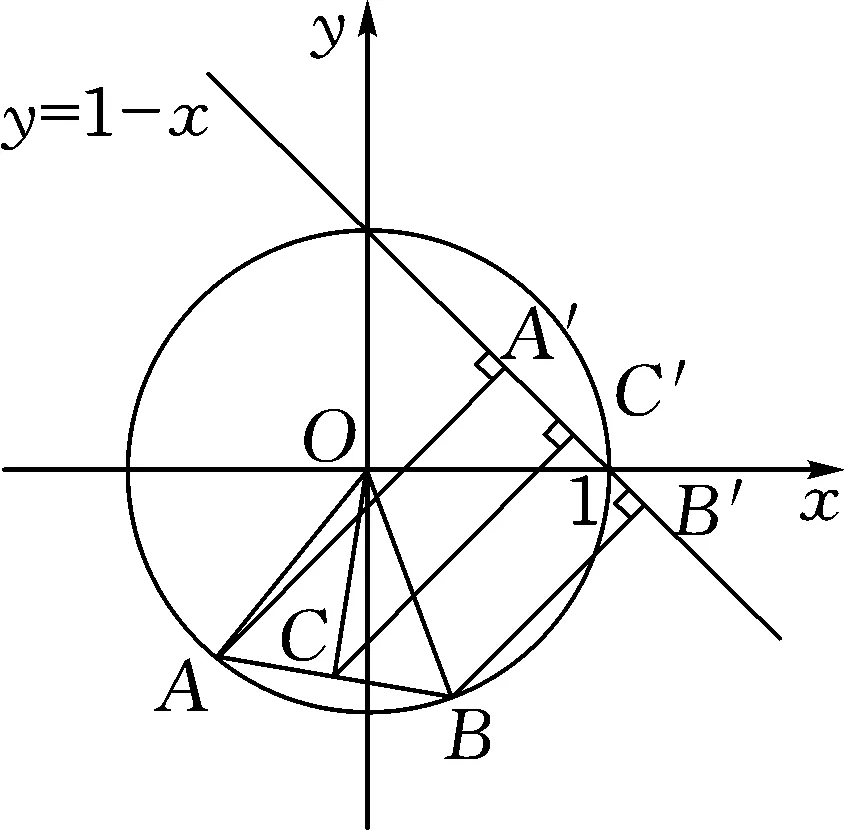
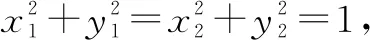

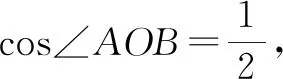
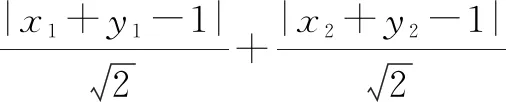
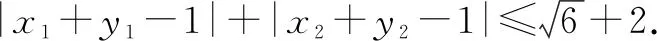

2.5 概念性问题
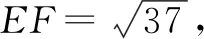

3 总结

