例谈不等式中的消元技巧
⦿浙江省宁波市鄞州中学 徐欣欣
1 引言
数学运算是高中数学学科核心素养之一,运算能力的缺乏已经严重掣肘学生数学学科核心素养的提升,笔者对数学运算中常用的技巧和思想加以总结,希望能助学生打破固有思路局限,拓展数学思维,并提升反思总结的能力.不等式问题中经常会碰到多变量问题,日常教学中,学生碰到不等式问题往往习惯性用不等式的性质去解.尽管部分多变量问题可以用不等式直接解决,但大多数时候若用消元处理则可以起到事半功倍的效果.本文中以不等式问题举例说明代入消元、整体换元消元、等价转化消元的运用.
2 消元法的应用技巧
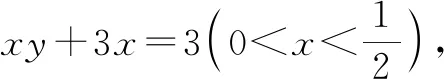
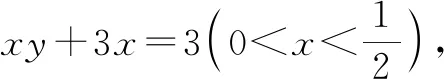
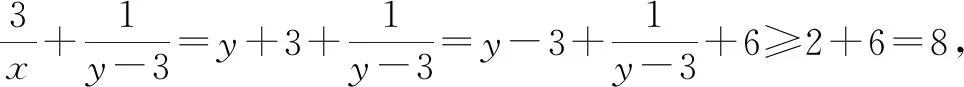
评注:该例题通过代入等式消元,转化为单变量的函数问题,若求最值则需要验证等号能否取到,若求范围则需要把函数定义域求解准确.代入消元是最基本的消元方法,经常使用.
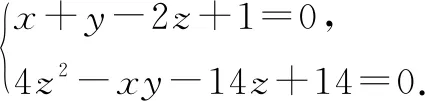
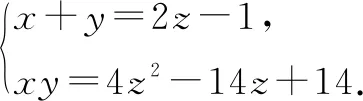
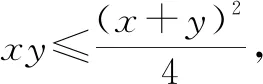
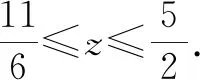
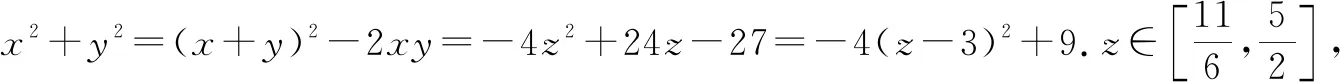
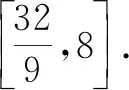
评注:该例题依旧是通过代入等式消元,转化为单变量的函数问题,但有所变化.已知条件中有x,y,z三个变量,而问题中只有x,y两个变量,常规想法是先消变量z,再消变量x或y,此题根据代数式特征直接消去了x,y变量,保留了z变量.
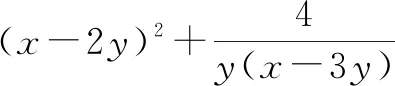
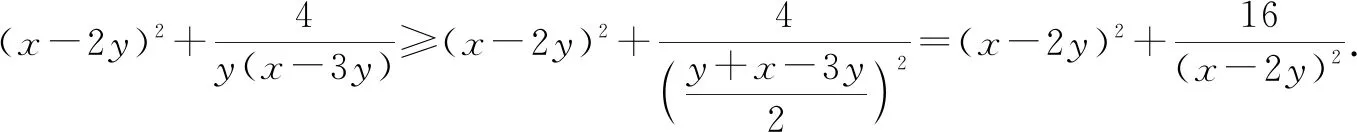
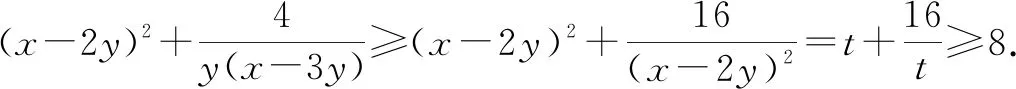
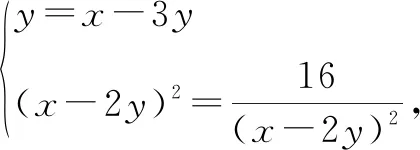
评注:该例题的关键是由y+(x-3y)=x-2y发现可以把x-2y看作一个整体,进行整体换元,从而达到消元目的.整体换元不仅可以把含两个变量的式子看作一个整体,也可把含三个、四个变量的式子看作一个整体,从而同时消去多个变量.
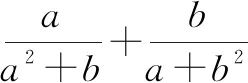
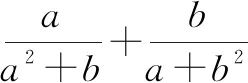
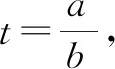
例5已知a>0,b>0,证明不等式:
证明因为a≠b,所以不妨设0 所以函数f(t)在区间(1,+∞)上单调递增,所以f(t)>f(1)=0. 例6已知实数a,b,c满足a2+2b2+3c2=1,则a+2b的最大值为. 解由a2+2b2+3c2=1,得a2+2b2≤1. 评注:该例题第一步通过等式转化为不等式从而达到消元效果.此过程看似简单,实则不易想到,关键是需要理解等价性,此题取到最值时存在满足条件的c即可. 代入消元有代入等式消元和代入不等式消元,代入不等式消元有时需要对代数式进行主元处理.比值消元作为整体换元消元中一类最常用的消元方式,往往需要对代数式进行齐次化处理.消元不仅在不等式问题中经常使用,对于其他情形的多变量问题,照样适用,而且对消元顺序的处理,往往能提供解题思路,所以培养学生的消元意识,学会消元技巧至关重要.Z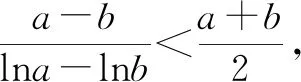
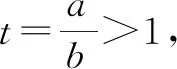
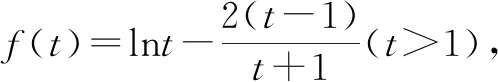
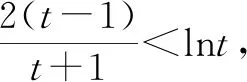

3 总结

